当“结果”变成“过程”
江苏无锡市花园实验小学(214000)李梅芝
当“结果”变成“过程”
江苏无锡市花园实验小学(214000)李梅芝
在小学数学教学中,教师往往更加关注学生对数学基础知识、基本技能的理解和掌握,而相对忽视知识的发生、发展和数学技能的形成过程。从“舍”和“得”、“进”与“退”两个角度着重讨论如何处理“结果”与“过程”的关系,阐述了教学中能够把结果变成过程,才能使学生逐步积累数学活动经验,感悟数学思想方法,才能把知识变成智慧。
过程结果数学活动经验思想方法
袁振国老师曾说过:“知识是启发智慧的手段,过程是结果的动态延伸。教学中能够把结果变成过程,才能把知识变成智慧。”当我真正把“结果”变成“过程”时,我能够感觉到,教室成为活力四射的地方,兴奋的目光、专注的神情,迫不及待的“我要补充”、“我要强调”、“我觉得他说的不对”、“还可以这样想”、“我要总结一下”……让我成了“旁观者”。作为教师的我不由感叹:“再也不能像以前那样‘讲’课了!”
一、有“舍”才有“得”
【案例1】二年级上册表内乘法练习课
教师出示题组一:
一共有多少个“△”。
(1)△△△△△△△△△△
(2)△△△△△△△△△△△△
(3)△△△△△△△△△△△△△△△△
学生解答后汇报:
生1:第(1)题得6+4=10。
生2:也可以是4+6=10。
生3:第(2)题得6×2=12。
生4:也可以是2×6=12。
生5:列加法也行,6+6=12。
生6:第(3)题得6×2+4=16。
生7:还可以是6+6+4=16。
生8:或者是6×3-2=16,第三堆填上两个就是6×3,再把2个去掉就减2。
(在这个过程中有学生忍不住插嘴,如提醒数数时要做记号,最好在图形下面标好数字,不要忘了写单位名称,等等,但教学过程还是比较顺畅的。)
生9:这些题都是求总数,都可以用加法算(边说边圈出三个加法算式)。
生10:但是第(1)题的两堆不同,不能用乘法,第(2)题的两堆都是6,可以用乘法。
生11:我反对,第(1)题也能用乘法。5×2=10,把第一堆的1个三角移到第二堆。(掌声响起)
师:为什么变化一下就能用乘法了?
生11:变得同样多了。
生12:第(3)题的前两堆一样用乘,后一堆不同用加。
生13:这样的话,第(1)题也可以写成4×2+2=10。
师:谁能解释这个算式?
生14:两堆都看成四个,再加上第一堆少看的两个。
生15:那也可以6×2-2,都看成6,再减去多看的2。
生16:我有个问题,都能用加法,为什么还用乘法?
生17:如果有100个6呢?用加法就太麻烦了呀!
生18:可以把乘法看成加法的儿子,当相同加数有很多的时候就用乘法算。
……
我本来准备了三个题组,还有若干个小练习,可是在第一组就花了差不多一节课时间。我总忍不住想打断学生的争论,但又不忍一盆冷水浇在燃烧的炭火上,这样的教学是成功还是失败呢?
或许有很多教师会说,这样怎么完成教学任务!在小学数学教学中,每个年级都有一些机动课时,低年段相对会更多一些。像二年级上册,教学用书上明确“全册教科书共安排了53课时的教学内容,另外还安排了4课时的期末复习。全学期大约有25%的教学时间留作机动,以便于教师创造性地安排教学。”而在实际教学中,这些机动课时多数被教师用来做练习课,大练、小练抑或补充题目,不舍得放弃任何一道题,还说:“因为做了还不会,还敢让他们不做吗!”期待反复的操练能带给学生更好的成绩!但是,反反复复做了学生就真的会了吗?是不是该错还是错,该不及格还是不及格?学生面对变化万千的题目,还是会像赵本山讲的一样“穿个马甲就不认识它了”。
上述案例中,教师没有一味地追求“结果”,而是尽可能留下较多的时间让学生探索、交流,让学生在发现问题、提出问题、分析问题、解决问题的过程中,积累基本的数学活动经验、增长智慧,增进人文情怀。细细品味,我们不得不承认,概念在“过程”中清晰,在“过程”中精致。
“舍得舍得”,有舍才有得,我们该学会舍弃,舍弃一些不做学生也会的,舍弃一些做了学生也不会的,舍弃一些教师的“告诉”和“强调”,把时间留给学生去发现、探究、经历。让学生在“过程”中获得进一步发展所需要的数学思想方法和必要的技能,让学生渐渐地学会运用数学的思维方式去解决遇到的问题,让学生慢慢地积累创新精神和实践能力,这才是“创造性地安排教学”。
不要满足于“结果”,让丰盈的“过程”给学生自我建构的机会,形成思考的策略,让倾听、思考、发现、交流、合作、创新成为学生的饕餮盛筵,成就“自然生长”的课堂。借用冯凌老师的话:“每个孩子都是一朵待放的花朵,作为教师的我们,闭上眼睛,或许便能听到每一朵花努力自主绽放的生命之声!”
二、有“退”才能“进”
【案例2】二年级上册表内乘除法练习课
算一算,比一比
4×45×56×6
3×5+14×6+15×7+1
师:比一比,有什么发现吗?
生1:我发现第一排式子的两个乘数都是相同的。
生2:第二排式子的两个乘数差2。
生3:第二排式子的每一道题都加1。
生4:上下两题的得数相同。
生5:我有补充,上面的乘数减1和加1后相乘再加1,得数是不变的。
师:为什么把上面的乘数分别减1和加1后得到的两个数相乘后再加1,得数会不变呢?是碰巧还是里面藏着什么秘密?请大家交流。
生6:我想画个图来说明,以第一组为例:
4×4表示4个4相加:|||| |||| |||| ||||
3×5可以表示3个5相加:
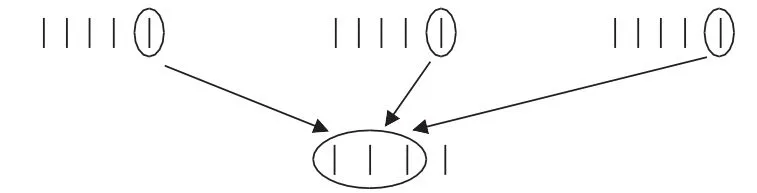
你看,3个5根再添上1根就是4个4根。
生7:第二组我来画。
……
师:有谁还能举出这样的例子?
生8:7×7=6×8+1。
师:算一算,相等吗?
生9:我有个问题,如果是1×1就不行了!
师:到底行不行?(出乎意料,停顿)大家试一试。
生10:行的,1×1=1=0×2+1不是也正好等于1吗?
师:0×2等于几?你怎么知道的?
生10:等于0,因为0×2就是0个2,就是一个也没有。
斯霞老师曾说过:“在课堂上,学生说的话要比教师说的多。”对数学课堂也是如此,教师给予学生的越多,学生的自主思维越容易被限制。学生往往习惯于顺着教师的思路一步步往前走,传统的课堂中只要出现“听懂了!”“学会了!”,就被认为教学目标完成了。
上述案例中,课堂不再是教师推出一个个问题,不再是师生一问一答的对话。从师生激烈的互相补充和争论中,能看到教师平时教学的影子,感受到教师平时教学中给予学生积累经验的时间和空间。不然,学生不会这么专注地倾听别人的发言,不会产生那么多独立的想法,更不会有这么敏锐的问题感和强烈的表现欲!我们可以感受到“学习过程正趋向于代替教学过程”。
这里,教师的“退”,让学生思维之河静静流淌。学生的不同想法,为课堂的进一步发展提供更多的话题与资源。“为什么把上面的乘数分别减1和加1后得到的两个数相乘后再加1,得数会不变呢?是碰巧还是里面藏着什么秘密?请大家交流。”教师的一句话,引领学生进入更深层次的思考。当学生争论不休时,教师没有随意地阻止,也没有直接给出答案,用“大家试一试”,以退为进给了学生独立思考和判断的时机。
教师的“退“,是“教”对“学”的退让。“退”并不是对学生放松要求,而是真正把学生放到课堂的中心位置,高度尊重学生,让课堂更多地充盈学生的声音。
教师的“进”,是“教”对“学”的推进。在围绕教学重难点等核心问题讨论时,教师的跟进能让学生的思维深入。在学生讨论无序时,教师的跟进是阻断不必要的纠缠;在学生交流迷失方向时,教师的跟进是及时的提醒;在学生概念含糊不清时,教师的跟进是恰当的点拨……要真正做到,该退的时候要退,该进的时候“点到即止”,从学生发展的角度对教与学的过程进行感知和判断,设身处地地为学生考虑,给予学生更多的学习空间,引导学生逐步走上“会学习”的道路。像周卫东老师说的:“此时的课堂正发生着‘悄悄的改变’,如潺潺溪流,如徐徐轻风,‘无痕’地改变着学生的经验系统,提升着学生的能力‘指数’。知识不是教学的终极目标,能力、对世界的看法、丰富的想象力等素养,才是教学的着眼点之所在!”
(责编金铃)
G623.5
A
1007-9068(2016)20-003

