一种改进的基于M2DPCA的人脸识别方法

武警警官学院　沈先耿　刘晓阳　李志军

一种改进的基于M2DPCA的人脸识别方法

武警警官学院沈先耿刘晓阳李志军

针对经典的M2DPCA算法存在总体散布矩阵构造不合理的问题。本文提出了一种改进的基于M2DPCA的人脸识别方法，该方法能够有效解决经典的M2DPCA算法存在的问题，并且后期通过对特征矩阵进行主成分分析处理，能够有效地提高算法的识别率和鲁棒性。

M2DPCA；人脸识别；总体散布矩阵

1　引言

经典的M2DPCA算法的基本思想是对人脸图像进行分块，将分块得到的子图像矩阵来构造总体散布矩阵，而后利用总体散布矩阵进行人脸图像的特征提取，与经典的2DPCA算法相比，该方法识别率较高，鲁棒性较好。但文献［1］表明，该算法存在总体散布矩阵构造不合理的问题。

其中协方差矩阵GT为一个零矩阵，这与实际是相符的，因为所有样本是相同的，它们在多元空间里是同一个点，也就是说它们之间不存在散度［2］。

但是，根据M2DPCA算法对总体散布矩阵的定义，计算得到子图像矩阵的总体散布矩阵明显不是零矩阵。

从上式中我们可以看出，原先不存在离散度的样本图像，由于采用分块而出现了离散度，并且能够求解出最优投影向量，这与实际不相符。因此，M2DPCA对于总体散布矩阵的定义不够合理，而本文算法将能有效解决总体散布矩阵构造不合理的问题。

2　算法步骤

训练开始阶段与M2DPCA的训练开始阶段相同，将维数为m×n的人脸训练样本进行分块，分成p×q个子块，每个子块的大小为m1×n1，其中。本文对M2DPCA的总体散布矩阵G2重新定义：

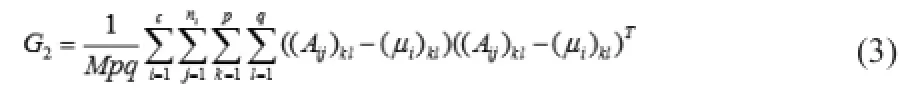
其中这里与传统的M2DPCA算法不同，在求样本子块的总体散布矩阵时不是采用所有训练样本子块的均值，而是采用所有训练样本子块的类内平均值。这样可以有效增加样本的类间距离，缩小样本的类内距离，同时也解决了总体散布矩阵定义不够合理的问题。因为当训练样本均相同时，可以得到：

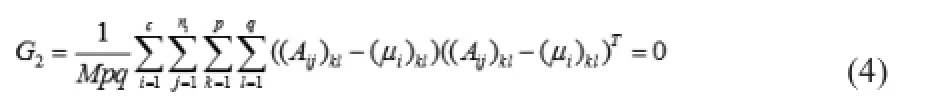
由公式（4）可以看出，G2的结果为0，样本间没有出现离散度，证明该方法是合理的，成功解决了M2DPCA算法总体散布矩阵构造不合理的问题。而后求解协方差矩阵G2的前r个最大特征值对应的特征向量，构成样本的最优投影矩阵，进而得到样本的特征矩阵。最后对特征矩阵进行PCA处理［3］，利用最近邻分类器完成分类识别。

3　实验结果分析

本文随机选取ORL人脸库中每个人的5张人脸图像作为实验的训练样本，余下的5张人脸图像作为待测人脸样本进行测试。为了增加实验的对比性，本文将经典的M2DPCA算法加入到相应的测试中，表1给出了两种算法在2×1、4×2、4×4、8×4、8×8、16×8和16×16等7种分块方式下采用10个鉴别矢量得到的算法识别率。

表1　7种分块方式下的识别率

从表1中可以看出，本文算法在不同的分块方式下，算法的识别率均高于经典的M2DPCA算法的识别率，具有较好的识别性能。但也可以看出，样本的分块并不是越多越好。不同大小的样本对分块数量的要求是完全不同的，如何根据不同的样本进行不同数量的分块仍然是一个值得深入研究的课题。

4　结论

本文根据M2DPCA存在的缺陷提出了一种混合M2DPCA+PCA的人脸识别方法，该方法能够克服M2DPCA方法存在的缺陷，实验表明该方法具有良好的识别率和鲁棒性。

［1］徐晓燕.人脸识别技术综述［J］.电子测试，2015，6（10）：31-35.

［2］田洪贞.基于嵌入式系统人脸识别方法的研究［D］.青岛：青岛科技大学，2012.

［3］羊牧.基于KL投影和奇异值分解相融合人脸识别方法的研究［D］.四川大学电子信息学院，2004.

沈先耿（1990—），山东章丘人，助教，研究方向为模式识别。

刘晓阳（1990—），山东长清人，助教，研究方向为图像处理。

李志军（1979—），广东中山人，助教，研究方向为网络工程。