基于BCABC-SVM的边坡稳定性预测*
胡 军,王凯凯,董建华
(辽宁科技大学 土木工程学院,辽宁 鞍山 114051)
基于BCABC-SVM的边坡稳定性预测*
胡军,王凯凯,董建华
(辽宁科技大学 土木工程学院,辽宁 鞍山 114051)
为了准确地对边坡稳定性进行预测,采用支持向量机(SVM)建立边坡稳定性和影响因素之间的非线性关系.针对支持向量机参数对预测效果的影响,采用基于细菌趋化的蜂群算法(BCABC)对其进行优化选择,提出了边坡稳定性预测的细菌趋化的蜂群优化支持向量机模型.运用该方法对边坡实例进行预测,预测结果与边坡稳定性实际状态相吻合,结果表明,基于细菌趋化的蜂群优化支持向量机模型在边坡稳定性评价中具有一定的可靠性和有效性.
边坡稳定;蜂群算法;细菌趋化;微粒群算法;自适应移动步长;支持向量机;参数选择;归一化处理
边坡稳定性预测一直是工程研究中的难题,通常评价的结果为是否稳定,不存在难以下结论的问题,最基本也是最普遍使用的方法可采用安全系数法.由于影响边坡的因素多且相互作用,导致了稳定性预测的精度不高.近些年发展的智能算法广泛应用于边坡稳定性分析,得出了比较理想的结果.许多学者采用标准支持向量机(SVM)的回归算法和分类算法对边坡稳定性问题进行了研究,取得了一定的效果.但其参数选择的随机性,既消耗了SVM的训练时间,又影响了SVM的预测精度.为了提高SVM的预测效率,本文将细菌趋化的蜂群算法应用到SVM的参数选择中,改进其参数选择的随机性,并用该模型对边坡实例进行了稳定性评价.
1 细菌趋化的蜂群算法
1.1标准蜂群算法
人工蜂群算法[1]通过模仿蜜蜂寻找优良蜜源的自组织行为,解决实际中的优化问题.在标准蜂群算法(ABC)中,每个蜜源的位置代表优化问题的一个可能解,蜜源的优良特性对应于问题的适应度值[2].待工蜂主要分为两类蜂群,分别为侦察蜂和跟随蜂.侦察蜂负责搜索蜜源,找到合适的空间范围的解.当某处的蜂源变差时,该处的其他蜜蜂立刻转化成侦察蜂.当搜索到较好蜜源时,侦察蜂也会作为一种引领蜂,指导跟随蜂的前进方向.跟随蜂得到引领蜂的信息分享,依照引领蜂种群适应值大小选择一个引领蜂,跟随其找到蜜源,并在其邻域内不断搜索新位置[3].当搜索到一定阶段,蜜源质量会降低,即在周围搜索次数Bas达到一定阈值Limit而仍没有找到更优位置时,为取得更好的搜索范围,采蜜蜂需放弃该蜜源,重新随机初始化更改蜜蜂的位置.
在蜂群算法的搜索过程中,每个食物源代表优化问题的一个可行解,侦察蜂的搜索行为可表示为
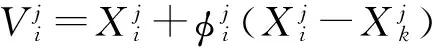
(1)
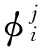
跟随蜂的搜索公式为
(2)
虽然人工蜂群算法(ABC)比其他优化算法具有全局高效搜索的优势,但由于其随机因子较多,寻优的后期收敛过快,收敛精度较低,面对复杂函数容易陷入局部最优.
1.2基于细菌趋化的蜂群算法
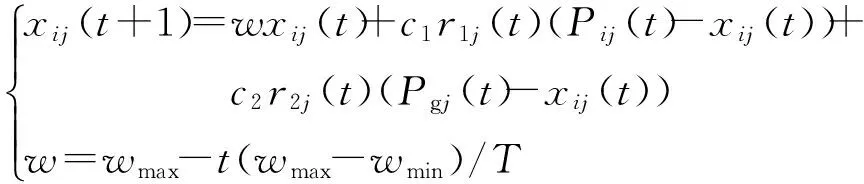
(3)
式中:xij为微粒i所经历的当前位置,下标j表示微粒的第j维;Pi为微粒i所经历的最好位置;Pg为所有微粒的全局最优位置;t表示第t代;T为最大迭代次数;wmin、wmax分别为惯性权重设置的最小值和最大值;c1、c2为加速常数,通常取[0,2]之间;r1、r2为两个相互独立的随机函数.当种群密度过大时,执行排斥操作,主要通过粒子的历史最差位置和群体最差位置来实现,寻优行为可表示为
xij(t+1)=wxij(t)-c1r1(t)(Wij(t)-xij(t))-
c2r2(t)(Wgj(t)-xij(t))
(4)
式中:Wi为微粒i所经历的最差位置;Wg为所有微粒的全局最差位置.
在此引入一种判断机制,蜜蜂周围拥挤度的系数m,其表达式为
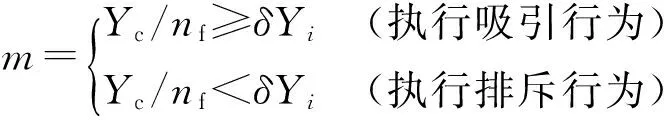
(5)
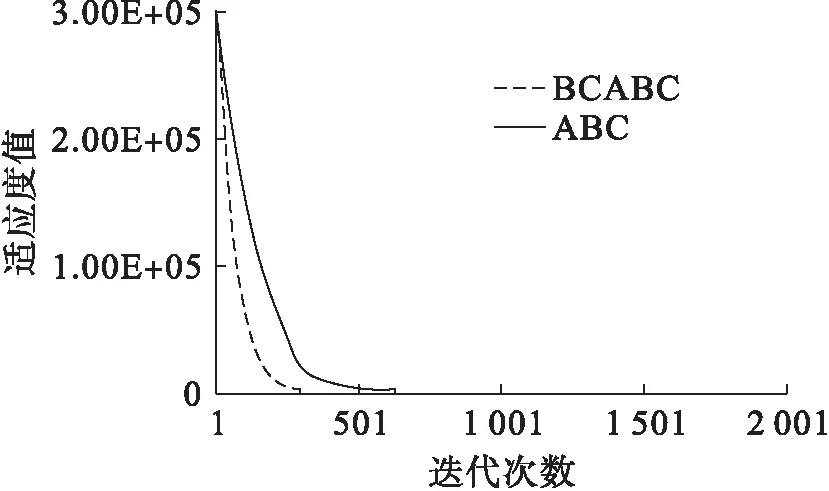
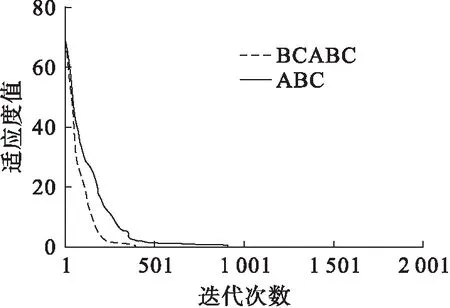
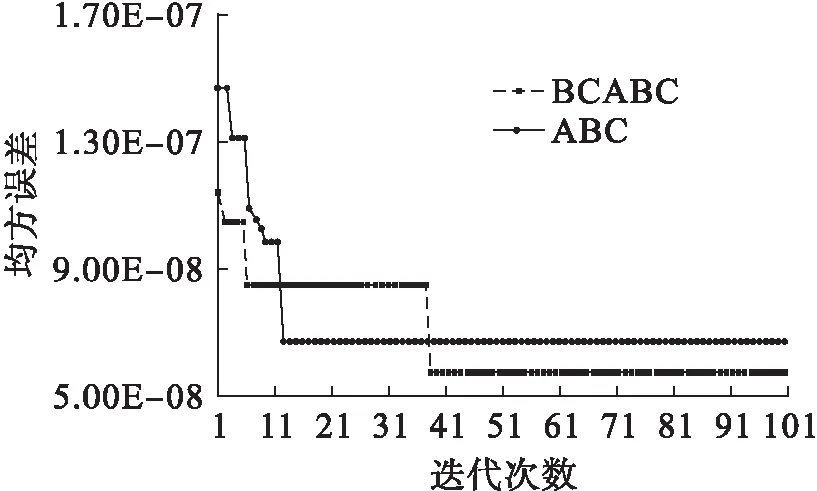
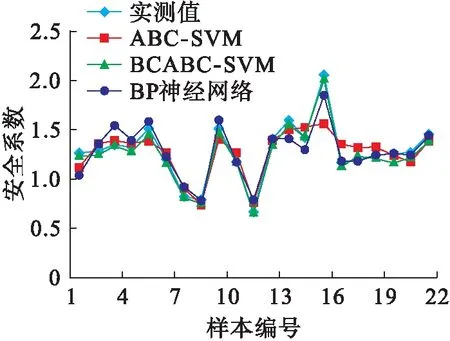
式中:Yi和Yc分别为蜜蜂i和中心位置蜜蜂的适应度值;nf为蜜蜂i当前邻域(dij 为了增加种群的多样性和局部寻优能力,在蜂群内跟随蜂的寻优行为中加入了细菌趋化思想来解决标准蜂群后期寻优精度不高等缺陷,并在侦察蜂的搜索公式中提出了自适应移动步长策略,以提高蜂群的全局搜索性能,其表达式为 (6) 式中:Step为移动步长;Stepmin、Stepmax分别为移动步长设置的最小值和最大值. 经过上述改进后,基于细菌趋化的蜂群算法(BCABC)的具体寻优步骤如图1所示. 图1 改进BCABC寻优流程图 1.3仿真试验 为了验证改进蜂群算法(BCABC)的有效性,本文分别运用标准蜂群(ABC)和细菌趋化的蜂群(BCABC)对以下3个经典测试函数进行仿真试验,同时为了保证结果的客观有效,采用30次独立试验取平均值. 1) Sphere函数,即 (7) 2) Griewank函数,即 (8) 3) Rastrigin函数,即 (9) 上述函数都是最小化优化函数,全局最优点均在x={0,0,…,0}处,且全局最优值均为0.其中,Sphere函数是一种单峰函数,其简单易实现,有助于增强测试算法在问题维度上的效果;Griewank函数是一种复杂的多峰三维函数,其复杂性在于函数存在大量的局部极值点,算法很容易陷入局部最优;Rastrigin函数是Sphere函数的多峰版本,具有大量按正弦拐点排列的、较深的局部最优点,有助于提高测试算法的全局搜索能力. 文献[5]中关于蜂群算法与粒子群算法在实例中的研究,在本次算法测试中,取d=100维的输入值,搜索空间取为[-100,100],标准蜂群算法(ABC)和改进蜂群算法(BCABC)各参数设置为:蜂群总数Ne=20,最大迭代次数T=2 000,搜索次数极限Limit=100,Visual=5,δ=0.2,wmax=0.9,wmin=0.1,Stepmax=10,Stepmin=1.测试结果见表1,寻优曲线如图2~4所示. 表1 测试函数对比 图2 Sphere函数算法寻优对比 由表1和图2~4可以看出,对于单峰函数,BCABC的精度提高较大,平均收敛精度提高了1012倍;但对于多峰函数,由于测试函数变得复杂,收敛曲线上ABC提早陷入了局部最优,BCABC很好地跳出局部极值,收敛精度提高了105倍.综上分析,BCABC经过细菌趋化改进,扩大了搜索空间,更容易跳出局部最优值,在收敛精度上有了很大的提升. 图3 Griewank函数算法寻优对比 支持向量机[6](support vector machine,SVM)作为统计学习理论最年轻的部分,是1995年由Vapnik和Corinna Cortes首先提出的,类似于神经网络的形式,在小样本、非线性及高维模式等问题表现出特有的优势.支持向量机主要通过构造一个分类超平面的决策曲面,使得正例和反例之间的隔离边缘被最大化;支持向量回归机也是应用了最大间隔算法,非线性函数可利用一个非线性映射,将训练数据集非线性映射到一个高维特征空间,通过高维特征空间中的线性学习算法获得,是结构风险最小化的近似实现. 图4 Rastrigin函数算法寻优对比 支持向量回归机的数学模型[7]为:设样本数据{xi,yi},i=1,2,…,l,其中,l为样本个数,xi∈Rn为输入变量,y∈R为输出变量,则回归估计问题简化为 (10) (i=1,2,…,l) (11) (12) (13) 对于非线性函数的回归问题,需利用核函数k(x,x′)代替点积[8],将式(13)改为 f(x)=w·k(x,x′)+b (14) 式中,k(x,x′)为回归向量机核函数.常用的核函数类型t主要有3种,分别是多项式函数、径向基函数和Sigmoid函数;回归SVM模型设置类型s主要有核支持向量机和ε-支持向量机;涉及支持向量机的主要参数还有惩罚参数c和核函数参数g. 支持向量机的样本训练,实际上是一个二次最优化问题[9].对于训练过程中的惩罚参数c和核函数参数g,一般是任意给定的或根据测试经验给定的,需要遍历网格内的所有参数点来寻求全局最优解,效率比较低下. 由于支持向量机的学习模型性能很大程度上依赖于参数的选择,以往穷举式的参数选择方法效率低下.结合细菌趋化的蜂群算法优良的全局搜索能力,本文采用细菌趋化的蜂群算法寻找SVM的最优参数组合,以此进行SVM样本训练和预测,具体步骤如下: 1) 根据实际问题,结合模型假设,筛选样本,确定问题的自变量和因变量; 2) 对样本进行归一化处理,对训练样本和预测样本都进行区间[0,1]归一化处理; 3) 选择合适的核函数; 4) 选择SVM参数,以SVM的惩罚参数c和核函数参数g为BCABC寻优变量,以SVM训练样本均方误差MSE作为适应度函数,利用细菌趋化的蜂群算法搜索最优的SVM参数; 纵观近两年中国白酒市场,茅台酱香系列酒的表现格外引人瞩目。去年,茅台酱香系列酒完成销量3万吨,实现销售收入65亿元,同比分别增长113%和169%,连续两年保持行业第一增长速度,成功挤入白酒上市公司前十名,形成“量效齐升”良好态势,由此成为中高端白酒消费的一支主流力量。 5) 将寻优得到的惩罚参数c和核函数参数g代入SVM,进行SVM训练和预测. 细菌趋化的蜂群算法优化支持向量机的具体实施步骤如图5所示. 图5 BCABC-SVM流程图 岩质边坡稳定性影响因素很多,如岩石容重、内聚力、内摩擦角、边坡角和边坡高度等.本文结合文献[10]收集的露天矿边坡评价实例,选取以上5个指标作为边坡稳定性评价的因素,如表2所示.选取前22个样本作为训练样本,后5个样本作为预测样本,利用细菌趋化的蜂群优化支持向量机进行边坡稳定性评价试验. 表2 训练样本与预测样本 4.1样本处理 为了提高SVM的泛化能力,首先对样本进行归一化处理.将样本点{xi}(i=1,2,…,l)归一化到区间[0,1],采用归一化映射,即 (15) 式中:x=(x1,x2,…,xl)为原始数据;y=(y1,y2,…,yl)为对应于x的归一化结果;min x、max x分别为样本x的最小值和最大值. 4.2模型参数的选择 本文选用SVM模型类型s=4(nu-support vector regression),核函数t=2(高斯RBF核函数),采用BCABC搜索SVM的惩罚参数c和核函数参数g,其取值范围均设定为(0,500).在细菌趋化的蜂群算法搜索中,以支持向量机训练样本的均方误差作为目标函数,种群各参数设置为:蜂群总数Ne=20,最大迭代次数T=100,搜索次数极限Limit=20,Visual=5,δ=0.2,wmax=0.9,wmin=0.1,Stepmax=10,Stepmin=1.利用BCABC寻优得出的SVM最优参数为c=12.24,g=85.59,适应度值即均方误差为5.78E-08,寻优曲线见图6. 图6 SVM参数寻优对比曲线 4.3样本训练与预测 利用BCABC寻优得到的参数对样本数据进行SVM训练和预测.为了验证本文模型在边坡稳定性评价的优越性能,分别采用BP神经网络算法、标准蜂群优化的支持向量机(ABC-SVM)进行实例的模拟试验,训练结果见图7,预测结果见表3. 图7 训练样本结果对比 由图7及表3可以看出,BCABC-SVM的预测精度较BP神经网络和ABC-SVM高达10%,寻优曲线上,BCABC-SVM比ABC-SVM较早达到稳定,并提前跳出局部极值,其网络模型的辨识精度较高.综上所述,BCABC-SVM的预测精度和全局搜索能力明显优于BP神经网络和ABC-SVM,说明用此模型进行边坡稳定性评价是可行的. 表3 预测样本结果对比 本文利用细菌趋化思想对标准蜂群算法进行了改进,改进后蜂群的排斥操作扩大了种群的搜索空间,吸引操作提高了种群的局部寻优能力,在仿真试验中得到了成功验证.将细菌趋化的蜂群算法用于支持向量机的参数选择,相比于以往的改进的支持向量机算法,本文模型更好地提高了支持向量机的泛化能力和预测精度,并成功将该模型应用到边坡稳定性评价系统中来,得出了较为准确的预测结果,具有一定的工程意义. [1]康飞,李俊杰,马震岳.基于人工蜂群算法的边坡最危险滑动面搜索 [J].防灾减灾工程学报,2011,31(2):166-172. (KANG Fei,LI Jun-jie,MA Zhen-yue.Searching for critical slip surface of slops based on artificial bee co-lony algorithm [J].Journal of Disaster Prevention and Mitigation Engineering,2011,31(2):166-172.) [2]宋腾蛟,陈剑平,张文,等.基于人工蜂群算法的岩体结构面多参数优势分组研究 [J].岩土力学,2015,36(3):861-868. (SONG Teng-jiao,CHEN Jian-ping,ZHANG Wen,et al.A method for multivariate parameter dominant parti-tioning of discontinuities of rock mass based on artificial bee colony algorithm [J].Rock and Soil Mechanics,2015,36(3):861-868.) [3]周悦,王丹,片锦香.基于蜂群算法的精密运动控制方法 [J].沈阳工业大学学报,2015,37(5):565-570. (ZHOU Yue,WANG Dan,PIAN Jin-xiang.Precision motion control method based on bee colony algorithm [J].Journal of Shenyang University of Technology,2015,37(5):565-570.) [4]周涛,崔德义,任书燕.基于细菌趋化的改进粒子群算法在电力系统无功优化中的应用 [J].上海电力学院学报,2014,30(8):315-323. (ZHOU Tao,CUI De-yi,REN Shu-yan.Application of particle swarm optimization based on bacterial chemotaxis to reactive power optimization [J].Journal of Shanghai University of Electric Power,2014,30(8):315-323.) [5]段海滨,张祥银,徐春芳.仿生智能计算 [M].北京:科学出版社,2011:88-94. (DUAN Hai-bin,ZHANG Xiang-yin,XU Chun-fang.Bio-inspired computing [M].Beijing:Science Press,2011:88-94.) [6]王小川,史峰,郁磊,等.MATLAB神经网络43个案例分析 [M].北京:北京航空航天大学出版社,2013:102-176. (WANG Xiao-chuan,SHI Feng,YU Lei,et al.Study on 43 cases of neural network by MATLAB [M].Beijing:Beihang University Press,2013:102-176.) [7]李长龙,潘伟强,胡盛龙.基于均匀设计的支持向量机参数优化方法 [J].计算机工程与科学,2014,36(4):702-706. (LI Chang-long,PAN Wei-qiang,HU Sheng-long.Parameter optimization method of SVM based on uniform design [J].Computer Engineering & Science,2014,36(4):702-706.) [8]马海兴,张刚.基于LS-SVM的边坡稳定性预测研究 [J].宁夏大学学报(自然科学版),2012,33(3):250-253. (MA Hai-xing,ZHANG Gang.Study on slope stability prediction based on LS-SVM [J].Journal of Ningxia University(Natural Science Edition),2012,33(3):250-253.) [9]邢宗义,冒玲丽,廖贵玲,等.基于PSO-SVM 模型的城轨列车轮对尺寸预测 [J].沈阳工业大学学报,2014,36(4):411-415. (XING Zong-yi,MAO Ling-li,LIAO Gui-ling,et al.Forecasting of wheelset size of urban rail train based on PSO-SVM model [J].Journal of Shenyang University of Technology,2014,36(4):411-415.) [10]薛锦春.矿山边坡岩体非线性力学分析与安全预警系统研究 [D].长沙:中南大学,2012:76-80. (XUE Jin-chun.Nonlinear mechanical analysis of rock mass and early warning security system in mine slope [D].Changsha:Central South University,2012:76-80.) (责任编辑:钟媛英文审校:尹淑英) Forecasting of slope stability based on BCABC-SVM HU Jun,WANG Kai-kai,DONG Jian-hua (School of Civil Engineering,University of Science and Technology Liaoning,Anshan 114051,China) In order to accurately forecast the slope stability,the nonlinear relationship between the slope stability and its influencing factors was established with adopting the support vector machine (SVM).Aiming at the effect of SVM parameters on the forecasting effect,the parameters were optimized and selected with bee colony algorithm based on bacterial chemotaxis (BCABC),and the BCABC-SVM model for the slope stability was proposed.This method was used to forecast the slope instance.The forecasting results are consistent with the actual states of slope stability.The results show that the BCABC-SVM model has a certain reliability and validity in the evaluation of slope stability. slope stability; bee colony algorithm; bacterial chemotaxis; particle swarm optimization algorithm; adaptive mobile step length; support vector machine (SVM); parameter selection; normalization processing 2015-06-08. 国家自然科学基金资助项目(51274053). 胡军(1977-),男,吉林白城人,教授,博士,主要从事尾矿坝稳定性监测和岩土边坡稳定性评价等方面的研究. 10.7688/j.issn.1000-1646.2016.02.19 TU 457 A 1000-1646(2016)02-0222-06 *本文已于2015-12-07 16∶16在中国知网优先数字出版.网络出版地址:http://www.cnki.net/kcms/detail/21.1189.T.20151207.1616.004.html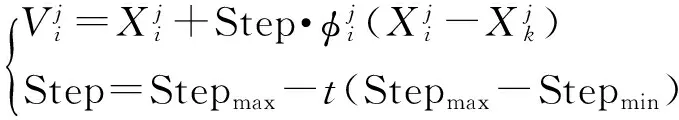


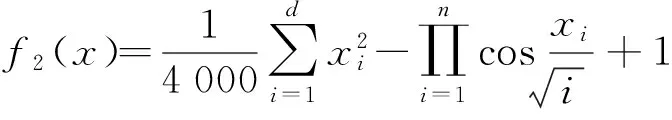


2 支持向量机原理


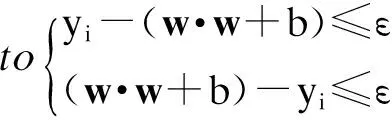

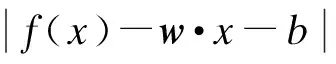
3 细菌趋化蜂群算法优化支持向量机

4 工程实例

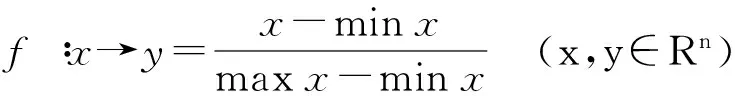

5 结 论

