永磁直线同步电机自适应PD型迭代学习控制*

赵希梅， 马志军， 朱国昕

(沈阳工业大学 电气工程学院， 沈阳 110870)



永磁直线同步电机自适应PD型迭代学习控制*

赵希梅， 马志军， 朱国昕

(沈阳工业大学 电气工程学院， 沈阳 110870)

针对永磁直线同步电机伺服系统易受摩擦力、端部效应和测量扰动等不确定因素影响的问题，提出一种自适应PD型迭代学习控制方法.该控制方法根据误差的大小在线智能地调整学习增益，从而抑制扰动，并在控制器的微分系数上引入指数学习增益，实现收敛速度与跟踪精度之间的折衷；从理论上证明了自适应PD型ILC的收敛性，分析了该控制算法的优越性.结果表明，与传统PD型ILC相比，自适应PD型ILC具有更快的收敛速度和更强的鲁棒性，大大地减小了跟踪误差.

永磁直线同步电机； 扰动； 自适应PD型ILC； 学习增益； 跟踪精度； 收敛速度； 鲁棒性； 跟踪误差

永磁直线同步电机(PMLSM)与传统“旋转电机+滚珠丝杠”的驱动方式相比，采用了直接驱动方式，其中间不需要任何的转换环节，具有推力大、损耗低、响应速度快、精度高等优点，近年来被广泛应用于工业领域[1-3].但参数变化、摩擦力、端部效应、测量扰动和齿槽力等扰动将毫无衰减地反映到电机动子及控制器上，增加了控制的难度[4-6]，因此，需要设计一个具有强跟踪性和强鲁棒性的控制器.

由于PMLSM伺服系统存在不确定性扰动，传统的PID反馈控制很难对PMLSM进行高精度跟踪控制.鲁棒控制虽然不需要系统的精确数学模型，但很难对直线电机的非线性完全补偿[7].文献[8]采用预测函数控制提高系统跟踪性能，具有较强的抗扰能力，但控制精度不高；文献[9]利用减小增益迭代学习实现一定区间内直线电机位置完全跟踪，但随着迭代次数的增加，收敛速度降低；文献[10]采用开环P型ILC补偿测量误差，但非重复性扰动使电机位置的波动较大.

针对上述问题，本文提出一种自适应PD型ILC方法，根据误差的大小在线调整控制器的学习增益，避免大的学习增益降低系统的跟踪精度，同时将指数学习增益引入到控制器的微分系数中，加快了收敛速度，最后，通过实验验证了所提出控制方法的有效性.

1　PMLSM数学模型

PMLSM的电磁推力方程[11]为

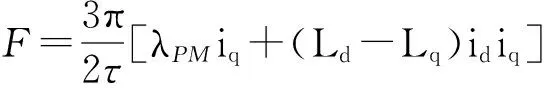
(1)

式中：F为电磁推力；τ为极距；id、iq分别为动子d、q轴电流；Ld、Lq分别为动子d、q轴电感；λPM为定子永磁体产生的励磁磁链.

对PMLSM进行矢量控制，电流内环采用磁场分量id=0 A的控制策略，使动子电流矢量与定子永磁体磁场在空间上正交，则PMLSM的推力方程为

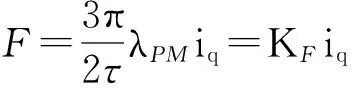
(2)

式中，KF为推力系数.机械运动方程为

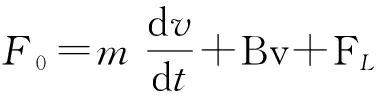
(3)

式中：m为动子质量；v为动子速度；B为粘滞摩擦系数；FL为负载阻力.PMLSM运行时，负载阻力FL主要包括摩擦力、端部效应和齿槽力，摩擦力可用LuGre模型[12]表示为

friction(v)=[fc+(fm-fc)e-(v/vs)2]sgn[v]

(4)

端部效应和齿槽力的表达式为

Fend(y)=A1cos(2πy/τ+θ)

(5)

Fslot(y)=A2sin(2πy/τ)

(6)

式中：fc为库仑摩擦力；fm为最大静摩擦力；vs为润滑系数；Fend为端部效应；Fslot为齿槽力；A1为端部效应的幅值；A2为齿槽力的幅值；y为动子输出位置；θ为初始相位电角度.

若取系统的状态变量为y和v，并设状态向量为x(t)=[y(t)，v(t)]T，由式(2)和式(3)可以推出PMLSM的状态方程为

(7)

2　控制系统设计

2.1PMLSM迭代学习控制系统

PMLSM的迭代学习控制系统框图如图1所示.ILC为自适应PD型迭代学习控制器，P为被控对象PMLSM，uk为第k次迭代的PMLSM输入控制信号，uk+1为第k+1次迭代的PMLSM输入控制信号，yd为给定的期望位置信号，yk+1为第k+1次迭代的系统输出位置信号，zk+1为第k+1次迭代的测量信号，ek+1为第k+1次迭代的位置误差，ηk+1为测量扰动信号，C为PD反馈控制器，增强系统的鲁棒性和稳定性.

图1　永磁直线同步电机迭代学习控制系统框图

2.2自适应PD型迭代学习控制器

在对系统进行分析前需要做出两个定义，定义测量误差为

ek(t)=yd(t)-zk(t)

(8)

由于迭代学习控制器的设计是为了提高跟踪期望轨迹的能力，即减小跟踪误差，所以定义跟踪误差为

εk(t)=yd(t)-yk(t)

(9)

由图1可以看出yk(t)=zk(t)-ηk(t)，结合式(8)和式(9)得出

ek(t)=εk(t)-ηk(t)

(10)

(11)

传统的PD型ILC学习律为

(12)

式中，K1、K2为两个恒定不变的学习增益.为了改善控制性能，设计学习增益在线调整的自适应PD型ILC学习律为

uk+1(t)=uk(t)+f(ek+1(t))[K3ek+1(t)+

(13)

式中：eβt为指数变增益函数，在闭环PD型ILC中可提高系统的收敛速度；f()为与误差边界α相关并随误差大小变化的非线性函数，其表达式为

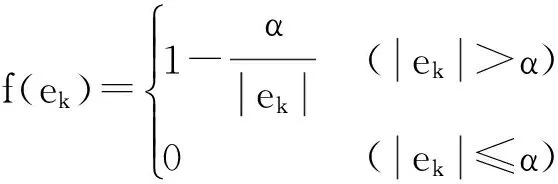
(14)

其变化曲线如图2所示.

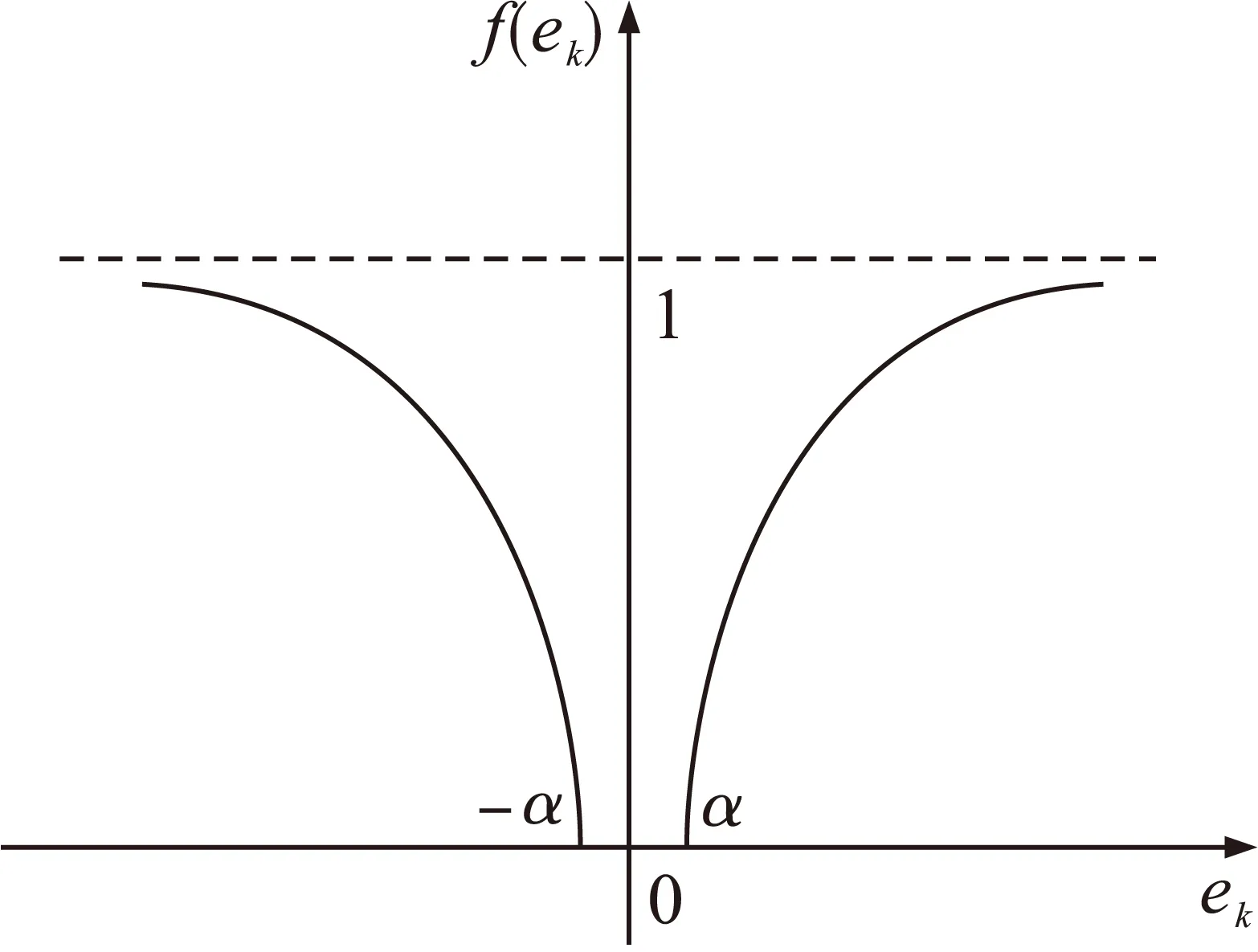
图2　增益函数f(ek)

式(14)结合式(13)可以得知，当误差较大时，控制器为含有指数增益的PD型ILC；当误差较小但大于α时，为变增益控制器，此时减小了学习增益，可提高控制精度；当误差小于α时，由于uk+1-uk=0，停止学习.由于测量扰动信号一般集中在幅值较小的范围，大的α使系统过滤掉过多有用的信号，因此，为了去掉扰动信号的同时保留有用信号，α应选择为小于测量扰动幅值并且小于误差幅值的值.

2.3收敛性分析

由于负载阻力FL(t)是与位置和速度相关的函数，PMLSM第k次运行的状态方程可表示为

(15)

式中，g为与位置相关的非线性函数.

引理假设控制系统的动态过程满足以下假设条件：

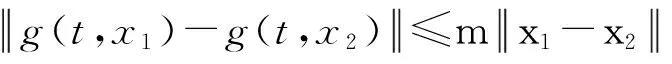
2) 每次运行的初始误差是一个收敛到0的序列；

3) 存在理想的控制信号ud(t)使系统状态和输出期望状态为xd(t)、yd(t)；

4) D(t)和ηk(t)有界；

5) I+K4eβtf(ek(t))CD(t)存在逆矩阵.

证明：

令g1(t，x)=g(t，xd(t))-g(t，xd(t)-x)，

∀x∈Rn

(16)

δuk(t)=ud(t)-uk(t)

(17)

δuk+1(t)=ud(t)-uk+1(t)

(18)

式(17)、(18)结合式(15)可以得到

δuk+1(t)=δuk(t)+uk(t)-uk+1(t)=

δuk(t)-(K3f(ek+1(t))ek+1(t)+

(19)

同时可以得到

εk(t)=yd(t)-yk(t)=Cδxk(t)

(20)

由式(20)和式(15)得

C[g(t，δxk+1(t))+D(t)δuk+1(t)]

(21)

式(21)结合式(11)可知

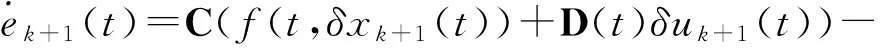
ηk+1(t)

(22)

故

δuk+1(t)=δuk(t)+uk(t)-uk+1(t)=

δuk(t)-K3f(ek+1(t))(Cδxk+1(t)-

ηk+1(t))-K4eβtf(ek+1(t))·

[C(g1(t，δxk+1(t))+D(t)δuk+1(t)-

ηk+1(t))]

(23)

由引理中的条件4)与式(23)可得

δuk+1(t)=(I+K4eβtCD(t))-1δuk(t)-

(I+K4eβtCD(t))-1(K3f(ek+1(t))·

(Cδxk+1(t)-ηk+1(t))+

K4eβtf(ek+1(t))[C(g1(t，δxk+1(t))-

ηk+1(t))]

(24)

令P(t)=(I+K4eβtCD(t))-1，则式(24)改写成

δuk+1(t)=P(t)δuk(t)-P(t)(K3f(ek+1(t))·

(Cδxk+1(t)-ηk+1(t))+

K4eβtf(ek+1(t))[C(g1(t，δxk+1(t))-

ηk+1(t))]

(25)

由式(15)可知

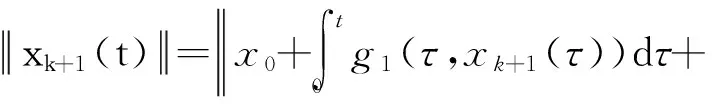
(26)

结合引理中条件1)，则

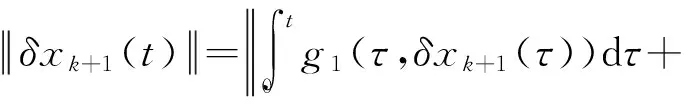
(27)

由Bellman-Gronwell引理和条件2)可知

(28)

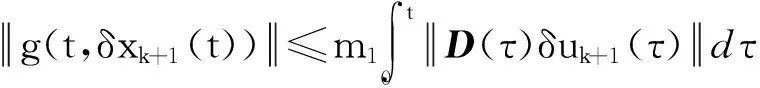
(29)

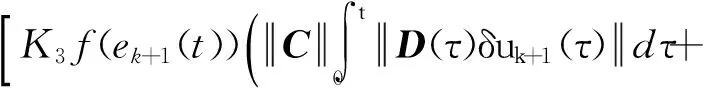
(30)

那么，存在与α和β相关的m2使

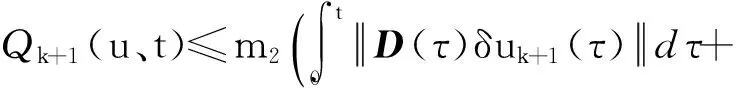
(31)

则式(24)可以写成

δuk+1(t)=(P+Qk+1(δuk、t))=

(P+Qk+1)(P+Qk)…

(P+Q1(δu0、t))

(32)

因此，可以得到

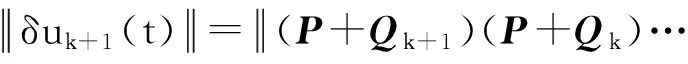
(33)

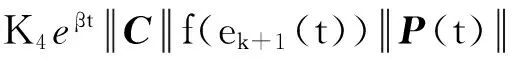
(34)

当误差小于α时，由式(30)可知，扰动和可用控制信号的系数都为0，因此达到高跟踪精度时系统停止学习，在满足收敛条件下，由式(30)和(33)可推出，存在与α和β相关的m4使

(35)

3　实验结果

基于DSP的PMLSM控制系统原理框图如图3所示，本实验采用TMS320LF2407ADSP为核心控制单元，驱动电路采用IPM，动子电流检测单元采用霍尔传感器，位置、速度检测采用直线光栅尺.PMLSM采用派克公司的I-Force系列110-2，直线电机的参数为：m=0.66kg，B=0.2N·s/m，R=1Ω，τ=60.96mm，p=4，Ψ=0.16Wb，L=8.5mH.PMLSM伺服系统的实验装置如图4所示.

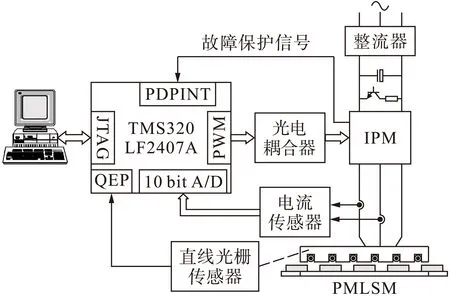
图3　PMLSM控制系统原理框图

图4　PMLSM控制系统实验装置

为了验证所提出控制方案的有效性，对基于PD型ILC的PMLSM伺服系统和基于自适应PD型ILC的PMLSM伺服系统进行实验对比研究.实验中给定的期望位置为

yd(t)=0.05sin(0.012 1t5-0.150 8t4+

0.502 7t3)

(36)

对式(36)中的位置进行跟踪，把均方根误差erms作为跟踪精度指标，其表达式为

(37)

式中：ε(j)为采样点误差；N为采样点数量.通过反复调试选取最优参数，PD型ILC的参数选择为K1=1 050、K2=1.5，反馈控制器的参数为KP=1 800、KD=0.05.实验测得非重复性扰动信号的幅值主要集中在20 μm以下，因此自适应PD型ILC的参数选取为K3=1 050、K4=1.5，α=8×10-8、β=1.13，反馈控制器与PD型ILC相同.

图5a为PD型ILC和自适应PD型ILC的位置跟踪曲线，图5b为PD型ILC迭代7次后的位置误差曲线，图5c为自适应PD型ILC迭代7次后的位置误差曲线.由图5b可知，传统PD型ILC的最大位置误差为18μm，从图5c可以看出，自适应PD型ILC的最大位置误差为10.5μm，经对比可知，最大位置误差减小了约2/5.

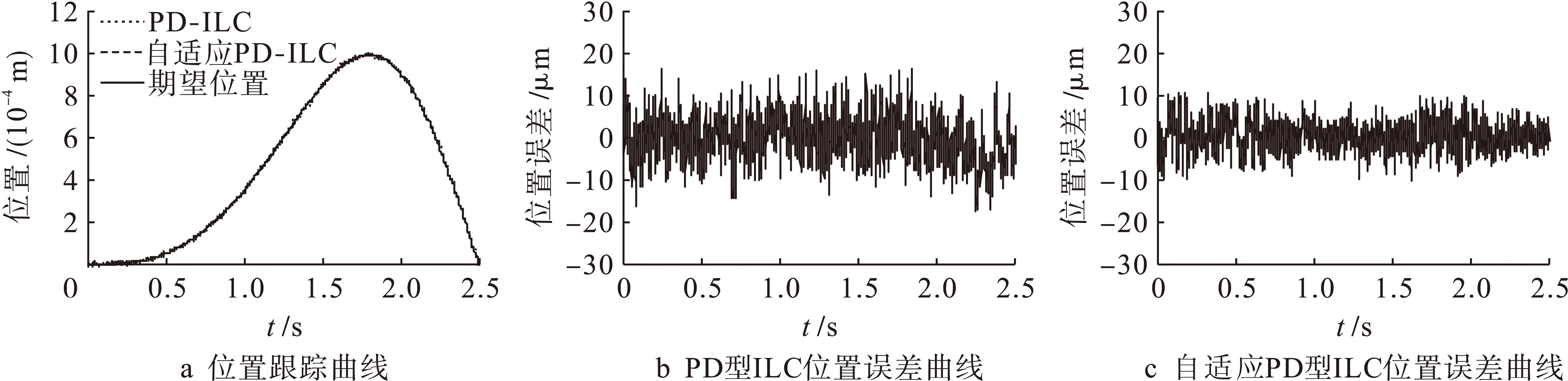
图5　PMLSM位置跟踪结果

图6为采用PD型ILC和自适应PD型ILC位置跟踪时均方根误差erms随迭代次数变化的曲线.由图可以看出，自适应PD型ILC迭代4次后的均方根误差小于PD型ILC迭代7次后的均方根误差，具有更快的收敛速度，减少了迭代次数，并且每次迭代的均方根误差比PD型ILC小.

图6　随迭代次数变化的均方根误差曲线

4　结　论

本文设计了一种自适应PD型ILC对PMLSM伺服系统进行跟踪控制研究，解决了一般控制方法要求精确的系统数学模型及无法对非线性完全进行补偿等问题，给出了系统收敛性的分析与证明.实验结果表明，所提出的自适应PD型ILC能有效地抑制扰动，减弱扰动在迭代过程中的积累，与传统的PD型ILC相比，自适应PD型ILC提高了控制精度，加快了收敛速度，具有很好的鲁棒性.

[1]王丽梅，武志涛，刘春芳.永磁直线伺服系统最优参数负载扰动补偿方法 [J].电工技术学报，2012，27(3)：133-138.

(WANG Li-mei，WU Zhi-tao，LIU Chun-fang.Optimal parameter load disturbance compensation method of permanent magnet linear servo system [J].Transa-ctions of China Electrotechnical Society，2012，27(3)：133-138.)

[2]杨俊友，刘永恒，白殿春，等.基于迭代学习与小波滤波器的永磁直线伺服系统扰动抑制 [J].电工技术学报，2013，28(3)：87-92.

(YANG Jun-you，LIU Yong-heng，BAI Dian-chun，et al.Disturbance rejection for PMLSM based on itera-tive learning control and wavelet filter [J].Transa-ctions of China Electrotechnical Society，2013，28(3)：87-92.)

[3]刘成颖，王昊，张敬之，等.基于非线性电感分析的永磁直线同步电机电磁推力特性研究 [J].中国电机工程学报，2011，31(30)：69-76.

(LIU Cheng-ying，WANG Hao，ZHANG Jing-zhi，et al.Research on thrust characteristics in permanent magnet linear synchronous motor based on analysis of nonlinear inductance [J].Proceedings of the CSEE，2011，31(30)：69-76.)

[4]Ma H，Yang S，Yang J Y，et al.Two-band filter compensation using lead phase iterative learning control with time window for PMLSM [C]//IEEE Conference on Industrial Electronics and Applications.Beijing，China，2011：737-742.

[5]闫光亚，艾武，陈冰，等.永磁直线同步电机ADRC控制系统 [J].电工技术学报，2011，26(9)：60-66.

(YAN Guang-ya，AI Wu，CHEN Bing，et al.PMLSM active disturbance rejection control [J].Transactions of China Electrotechnical Society，2011，26(9)：60-66.)

[6]党选举，徐小平，于晓明，等.永磁同步直线电机的小波神经网络控制 [J].电机与控制学报，2013，17(1)：43-49.

(DANG Xuan-ju，XU Xiao-ping，YU Xiao-ming，et al.Control for PMLSM based on wavelet neural network [J].Electric Machines and Control，2013，17(1)：43-49.)

[7]王丽梅，史佳林，许长林.基于H∞LTR综合方法的永磁直线同步电机鲁棒控制 [J].沈阳工业大学学报，2013，35(3)：241-245.

(WANG Li-mei，SHI Jia-lin，XU Chang-lin.Robust control for permanent-magnet linear synchronous motor based onH∞synthetic method [J].Journal of Shenyang University of Technology，2013，35(3)：241-245.)

[8]夏泽中，张光明.预测函数控制及其在伺服系统中的仿真研究 [J].中国电机工程学报，2005，25(14)：130-134.

(XIA Ze-zhong，ZHANG Guang-ming.Design and evaluation of predictive functional control for a servo system [J].Proceedings of the CSEE，2005，25(14)：130-134.)

[9]张宏伟，余发山，卜旭辉，等.基于鲁棒迭代学习的永磁直线电机控制 [J].电机与控制学报，2012，16(6)：81-86.

(ZHANG Hong-wei，YU Fa-shan，BU Xu-hui，et al.Robust iterative learning control for permanent magnet linear motor [J].Electric Machines and Control，2012，16(6)：81-86.)

[10]Teo C S，Tan K K，Lim S Y.Dynamic geometric compensation for gantry stage using iterative learning control [J].IEEE Transactions on Instrumentation and Measurement，2008，57(2)：413-419.

[11]杨俊友，刘江华，邱桂林，等.基于预测电压调制与 T-S模糊PMLSM推力控制 [J].沈阳工业大学学报，2012，34(4)：361-365.

(YANG Jun-you，LIU Jiang-hua，QIU Gui-lin，et al.Thrust control of PMLSM based on predictive voltage modulation and T-S fuzzy control [J].Journal of Shen-yang University of Technology，2012，34(4)：361-365.)

[12]Chen S L，Tan K K，Huang S N，et al.Modeling and compensation of ripples and friction in permanent-magnet linear motor using a hysteretic rely [J].IEEE Transactions on Mechatronics，2010，15(4)：586-594.

(责任编辑：景勇英文审校：尹淑英)

Adaptive PD-type iterative learning control for permanent magnet linear synchronous motor

ZHAO Xi-mei, MA Zhi-jun, ZHU Guo-xin

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)

In order to solve the problem that the servo system of permanent magnet linear synchronous motor (PMLSM) is easily affected by such uncertainty factors as friction, end effect and measurement disturbance, an adaptive PD-type iterative learning control (ILC) method was proposed. According to the size of the error, the control method could intelligently adjust the learning gain so as to restrain the disturbance. Simultaneously, the exponential learning gain was introduced for the differential coefficient, which could achieve the compromise between both convergence rate and tracking precision. The convergence of adaptive PD-type ILC was theoretically proved, and the superiority of the proposed control algorithm was analyzed. The results indicate that compared with the traditional PD-type ILC, the adaptive PD-type ILC has faster convergence rate and stronger robustness, and can greatly reduce the tracking error.

permanent magnet linear synchronous motor (PMLSM); disturbance; adaptive PD-type ILC; learning gain; tracking precision; convergence rate; robustness; tracking error

2015-05-26.

国家自然科学基金资助项目(51175349)； 辽宁省教育厅科学技术研究项目(L2013060)； 沈阳市科技计划资助项目(F12-277-1-70).

赵希梅(1979-)，女，吉林德惠人，副教授，主要从事直线伺服、数控技术及鲁棒控制等方面的研究.

10.7688/j.issn.1000-1646.2016.01.02

TM 315

A

1000-1646(2016)01-0007-06

*本文已于2015-12-07 16∶16在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20151207.1616.010.html