一类KdV型方程的不变子空间

屈改珠

(渭南师范学院 数理学院,陕西 渭南　714000)



一类KdV型方程的不变子空间

屈改珠

(渭南师范学院 数理学院,陕西 渭南714000)

讨论了一类KdV型方程的不变子空间，通过分别考虑其二维和三维不变子空间，构造了方程的不同形式的广义分离变量解，得到了一些方程的尖峰孤子解和爆破解。

不变子空间；KdV型方程；广义分离变量解；尖峰孤子解；爆破解

0　引言

本文研究一类带有源项的KdV型方程

ut=F[u]=αuxxx+β(ux)2+γu2，

(1)

当α=β=1,γ=0时，方程(1)成为势KdV方程

ut=uxxx+(ux)2。

(2)

方程(2)是通过对著名的KdV方程vt=vxxx+2vvx施行变换v=ux而得到的。

不变子空间方法是与广义条件对称[1-4]密切相关的构造非线性偏微分方程(组)广义变量分离解的有效方法之一。下面介绍不变子空间方法及相关定义[5-9]。考虑一阶演化方程

ut=F[u]，

(3)

其中F[u]≡F(x,u,ux,…,ukx)是一个k阶非线性微分算子，F(·)是充分光滑的函数，ukx表示u关于x的k阶导数，由n个线性无关的函数f1(x),…,fn(x)扩张生成的n维线性空间

其中Ci(t)满足下面的有限维动力系统：

(4)

从(4)可以得到Wn关于F的不变条件为

(5)

这里用[H]表示方程L[u]=0以及它关于x求各阶导数后的等式.

1　微分算子F[u]容许的不变子空间

我们考虑方程(1)中微分算子F[u]允许的不变子空间，根据不变子空间理论中的最大维定理，算子F[u]所容许的不变子空间的最高维数为7，通过计算可知，算子F[u]仅在W2和W3上有非平凡解。

1.1二维不变子空间W2

考虑方程(1)算子F[u]中容许的二维不变子空间W2，W2由如下线性常微分方程定义

L[y]=y″+a1y′+a0y=0，

(6)

则相应的不变条件变为

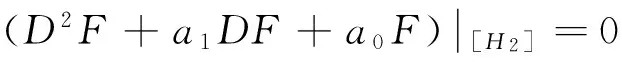
(7)

其中[H2]表示约束条件：L[u]=0及其关于x求导后的等式。经计算，(7)式左端为关于变量u,ux的多项式，令方程中各项系数为0，得到下列方程组

利用maple求解上述代数方程组，得到其非平凡解：

将其代入到(1)及(6)中，有下面的结果

1.2三维不变子空间

同样的，我们给出在方程(1)中非线性微分算子F[u]允许的由方程(4)定义的三维不变子空间，W3由如下线性常微分方程定义

L[y]=y‴+a2y″+a1y′+a0y=0，

(8)

则相应的不变条件变为

(9)

从而(9)式左端为关于变量u,ux,uxx的多项式，令方程中各项系数为0，得到下列方程组

用maple 求解得到

将其代入到方程(1)及(8)中，有

2　例子

例1考虑方程

(10)

它容许三维多项式不变子空间

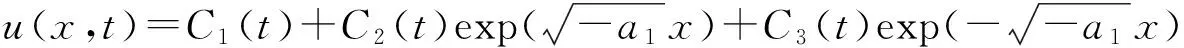
其中Ci(t)满足下面的常微分方程组

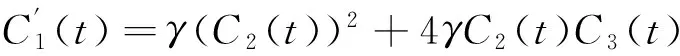
求解上述方程组，可得原方程具有尖峰孤子解

c1是任意实数。

c1,c2是任意实数。

[1] FOKAS A S,LIU Q M.Generalized conditional symmetries and exact solutions of nonintegrable equations[J].Theor Math Phys,1994,99:263-277.

[2] FOKAS A S,LIU Q M.Nonlinear interaction of traveling waves of nonintegrable equations[J].Phys Rev Lett,1994,72:3293-3296.

[3] ZHDANOV R Z.Conditional Lie-Backlund symmetry and reduction of evolution equations[J].J Phys A:Math Gen,1995,28:3841-3850.

[4] QU C Z.Group classification and generalized conditional symmetry reduction of the nonlinear diffusion convection equation with a nonlinear source[J].Stud Appl Math,1997,99:107-136.

[5] GALAKTIONOV V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities[J].Proc Royal Soc Edinburgh,1995,125:225-246.

[6] SVIRSHCHEVSKII S R.Symmetries of linear ODEs and generalized separation of variables in nonlinear equations[J].Phys Lett A,1995,199:344-348.

[7] GALAKTIONOV V A,SVIRSHCHEVSKII S R.Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics[M].London:Chapman and Hall/CRC,2007.

[8] QU C Z,ZHU C R.Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J].J Phys A:Math Theor,2009,42:475201-475227.

[9] MA W X.A refined invariant subspace method and applications to evolution equations[J].Sci China Math,2012,55:1769-1778.

The invariant subspaces for a family of KdV-type equations

QU Gaizhu

(School of Mathematics and Physics, Weinan Normal University, Weinan，Shannxi 714000,China)

Invariant subspace of a family of KdV-type equations are discussed.By studying two-dimension and three-dimension invariant subspace, several different types of separation of variables solutions are obtained. Peak solutions and blow-up solutions of some equations are also derived.

invariant subspace；KdV-type equations；generalized separation of variables solution；peak solution；blow-up solution

1004—5570(2016)04-0051-03

2016-04-10

国家自然科学基金资助项目(11371293，11501419)；陕西省重点学科数学学科基金项目(14SXZD015)；渭南师范学院理工类科研项目(16ZRRC05,13YKF003), 渭南师范学院校级特色学科建设项目(14TSXK02)

屈改珠(1978-), 女,讲师，博士研究生,研究方向：偏微分方程，E-mail：qugaizhu.hi@163.com.

O175.29

A