把握学习起点，有效设计教学

浙江余姚市教师进修学校（315400） 王国元

把握学习起点，有效设计教学

浙江余姚市教师进修学校（315400） 王国元

教学设计要依托学生的学习起点。教师在充分了解学生学习起点的基础上，选择合适的教法，设计有针对性的学法，充分调动学生的学习主动性，从而真正实现“以生为本”的教育理念。

前测学习起点把握实践思考

在教学中，教师应以学生的认知发展水平和已有经验为基础，准确把握学生的学习起点，并以此为依据进行教学设计与学法指导，以促进学生更好地发展。

一、学习起点的内涵

学习起点是指学生在当前状态下已有的“四基起点”（包括知识起点、技能起点、经验起点和数学思想起点）与“情感态度起点”的总和。知识起点是指学生已有的知识网络，并具有不断更新、重组的功能。技能起点是指学生运用已有的数学知识去发现问题、提出问题、分析问题、解决问题等能力。经验起点是指学生已有的生活经验和基本活动经验，其主体指的是学生的思维经验。数学思想起点是指学生已有的对抽象、推理、模型等思想的感悟与应用。情感态度起点是指学生学习新知识时所具备的心理状态，包括面对新的学习对象时产生的好奇心、求知欲、自信心等。学生的学习起点具体可用如下三维图来表示。

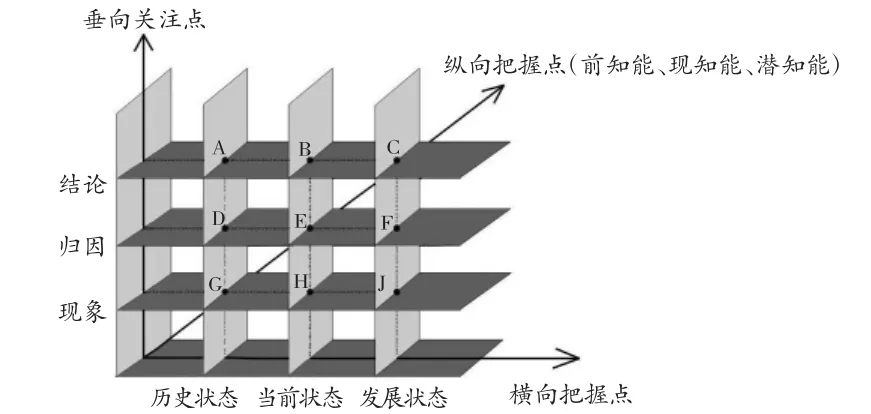
学生的发展是“立体式”的。其发展过程状态有历史状态、当前状态和发展状态。每种状态都与学生某一阶段学习的现象、归因、结论三个层面产生交点，即A、B、…、I共9个交点，27个维度。每个交点都应从学生的“四基起点”与“情感态度起点”进行分析和把握。

二、把握学习起点的价值

1.把握学习起点是学生有效学习的前提

有效学习是指在一定的学习时空内，学生学习的效率高、效果佳。学生的学习具有阶段性与连续性的特点，同时由于个体差异的存在，不同的学生在学习同一内容时，所表现出的思维方式、行为态度、领悟水平等也均不相同。因此，把握学生的学习起点，可以使不同程度的学生在其原有认知水平的基础上，生长出新的认知点，从而使学习更高效。

2.把握学习起点是教师有效设计的前提

备课要“备教材”，更要“备学生”。然而在课堂设计中，教师往往只关注“备教材”，即注重知识的逻辑结构，而忽视了学生的实际情况。把握学生的学习起点，就是要重点把握学生已经具备了哪些知识和能力？哪些是学习中的断层和难点？哪些学生的学习能力较强（或较弱）？如何根据学生的发展需求创设有效的活动以引导他们积极参与……由此可见，把握学生的学习起点为教师有效的教学设计提供了现实依据。

三、把握学习起点的原则

1.发展性原则

学生是学习的主体，也是一个不断发展变化着的个体。由于学生具有主观能动性，在受到外界的刺激与作用下，其认知结构不断地重组、构建着，并按横向延拓、纵向螺旋上升的方式向更高层次发展，在过去、现在、将来都具有不同的表现。把握学习起点就要以动态发展的眼光看待学生，努力使学生潜在的发展可能性在有效的刺激下成为现实。

2.针对性原则

学生在学习新知识时受多种因素的影响，因而其在某一阶段获得新的发展之前，在不同方面具有不同的起点。教师应针对学习内容把握学生的“四基起点”和“情感态度起点”。

3.科学性原则

在把握学生的学习起点时要做到科学、合理。具体如下：

方法科学——根据学生的年龄特点和所学内容，编拟恰当的前测题目，选择合理的前测方法。

数据真实——前测过程中，在对收集的数据进行整理时，做到尊重事实，直面结果。

分析合理——依据前测获得的相关信息进行科学、合理的分析，从而得到符合学生实际情况的、真实可靠的结论。

四、把握学习起点的步骤与方法

1.把握学习起点的步骤

第一步：编拟前测题目。根据学习内容和目标，结合学生的年龄特点和认知规律，有针对性地从“四基起点”和“情感态度起点”两方面编拟前测题目。

第二步：确定前测方法。由前测题目和学生特点，确定前测方法。常用的前测方法有测试法、访谈法、操作法、观察法、作业痕迹分析法等。

第三步：实施前测。前测时，必须向学生说明前测意图，营造宽松、和谐的环境。并根据编拟的题目和确定的方法具体实施，以文字、表格、录音等方式记录过程和结果，以真实反映学生的当前状态。

第四步：汇总前测结果。根据原始记录，分类、整理、统计各项相关信息，为科学合理地分析学习起点奠定基础。

第五步：分析并确定学习起点。立足前测汇总的结果，分别从历史状态、当前状态、发展状态的现象、归因、结论对学生的学习起点进行全面的分析，以确定学习起点，从而为有效的“教”和“学”提供科学的依据。

2.把握学习起点的方法

测试法——前测题目以文字的形式呈现，以笔试的方式进行。测试时要引导学生认真对待、仔细审题、独立完成。

访谈法——根据前测题目，教师与学生逐题、逐个面对面地进行交谈。教师只倾听学生的表达，不作任何提示、引导和评价，可作适当的追问，并在事先设计的访谈记录表中及时做好记录，且进行同步录音。

操作法——学生根据教师创设的问题情境，通过操作活动尝试解决问题。提供的操作材料要多元多样，以便学生自主选择。操作时，学生逐个在教师面前进行，教师仔细观察操作过程和结果，并认真记录。

观察法——在进行访谈和操作的过程中，对学生的学习方式、学习表情和态度等进行观察。在观察过程中，教师对学生的表现不作任何提示与评价。

作业痕迹分析法——对学生作业中的书写过程、书写格式、修改痕迹、独特的算法和典型错误等进行分析。重点关注独特的算法和典型错误，并对典型错误作归因分析，必要时进行访谈。

五、实践与思考

下面以“圆的面积”一课为例，谈谈对如何把握学习起点和根据学习起点确定教学对策的思考。

1.前测题目和方法

（1）检测经验和数学思想起点。请你说一说，平行四边形、三角形和梯形的面积计算公式是如何推导出来的？（提供操作材料：平行四边形、三角形和梯形图，相应纸片、剪刀、笔）【采用访谈法、操作法、观察法】

（2）检测情感态度起点。学习圆的面积的计算，你有没有兴趣和信心？为什么？【采用访谈法】

（3）检测知识起点。圆的面积指的是什么？你会求圆的面积吗？如会则追问：“怎么知道的？”（提供操作材料：圆形纸片）【采用访谈法、操作法、观察法】

（4）检测技能和经验起点。怎样推导圆的面积的计算公式？在推导中有什么困难？（提供操作材料：圆形纸片、剪刀）【采用访谈法、操作法、观察法】

2.实施前测（略）

3.汇总前测结果（略）

4.分析并确定学习起点

根据前测数据统计，对该班学生的学习起点分析如下。

（1）四基起点。

知识起点：对圆的面积的意义理解比较到位，100%的学生能用不同的方式正确描述。40%的学生通过各种途径已经知道圆的面积的计算公式。

技能起点：有37.8%的学生能尝试用实物操作、画图等方法探究圆的面积的计算公式，但仅有11.1%的学生能正确描述推导的过程。

经验起点：绝大部分学生已积累了用割补、分割、倍拼等方法，将未知的平面图形转化为已知的平面图形，从而推导出未知平面图形的面积计算公式。但学生缺乏用“化曲为直”的方法把曲线平面图形转化为直线平面图形的经验，虽有40%的学生知道圆的面积的计算公式，但仅有11.1%的学生能正确描述推导过程（这些学生已提前在培训班中学习过）。

数学思想起点：根据已有经验，有95%以上的学生已感悟到可以用转化的数学思想推导面积计算公式，因此有37.8%的学生尝试用这一数学思想进行圆的面积计算公式的推导。由于缺乏极限的数学思想，学生在用“化曲为直”的方法进行面积计算公式推导的过程中，26.7%的学生尝试推导失败，62.2%的学生则无从下手。

（2）情感态度起点。

由于第一次探究曲线平面图形的面积计算公式，有97.8%的学生有浓厚的学习兴趣和强烈的学习欲望，这为成功学习圆的面积计算公式的推导提供了良好的心理条件。

5.教学对策

（1）调动已有经验，尝试用转化思想进行推导。在回顾割补、倍拼方法的基础上，让学生尝试推导圆的面积的计算公式。当尝试失败后，讨论失败的原因在于圆是曲线平面图形，进而引导学生用割补的方法化曲为直进行推导。在推导时引发学生思考：“怎么割（沿直径、半径还是其他）？割成几份？怎么补？”学生经过操作发现，只有沿半径割，且要割成同样大小的图形才能转化为近似长方形。

（2）借助操作想象，尝试用极限思想化曲为直进行推导。为了使学生感悟到割的份数越多，拼成的图形越接近长方形，可引导学生经历以下三个层次的学习过程。

第一层次：操作比较，初步感受等分的份数越多，拼成的长方形的长边就越直，这个图形越接近长方形。

第二层次：观察感知，等分的份数越多，长边就越直，这个图形越接近长方形。课件演示，引导学生观察把圆分别等分成32份、64份后拼成的近似长方形的长边的变化情况。

第三层次：想象推理，初步感悟极限思想。引导学生想象并思考：“要使长边变成直的线，应该分成多少等份？”

综上所述，只有尊重学生学习起点和认知规律的教学设计，才能使学生在课堂中真正获得知识和技能，从而感悟数学基本思想。

（责编李琪琦）

G623.5

A

1007-9068（2016）23-054