一种理想弹塑性模拟的冰材料本构模型

胡志强，高 岩，姚 琪

（1. 上海交通大学海洋工程国家重点实验室，上海 200240；2. 上海交通大学高新船舶与深海开发装备协同创新中心，上海 200240）

一种理想弹塑性模拟的冰材料本构模型

胡志强1，2，高 岩1，姚 琪1

（1. 上海交通大学海洋工程国家重点实验室，上海 200240；
2. 上海交通大学高新船舶与深海开发装备协同创新中心，上海 200240）

船冰碰撞是船舶碰撞研究领域的热点之一，对冰材料的模拟是船冰碰撞的研究重点。提出一种利用理想弹塑性模型模拟的冰材料本构模型，利用半隐式图形算法计算单元塑性阶段的应力，利用Tsai-Wu屈服准则和经验失效公式用来描述冰的力学行为。利用二次开发功能，将冰材料模型嵌入LS_DYNA程序，并验证该模型的准确性和适用性。研究中针对不同局部形状的冰块与船侧碰撞场景，通过比较分析碰撞力、能量耗散等，探讨冰块的局部形状对碰撞场景的影响。研究结果表明：冰材料模型在大接触面的条件下压力与已有标准吻合较好；在不同的冰块局部形状条件下，船冰碰撞的相互作用过程不同；较钝形状的冰块表现近乎刚体，较尖锐形状的冰块较易破碎。

船冰碰撞；弹塑性材料；本构模型；冰块形状影响；数值仿真

0 引 言

近年来，随着在极地地区航行的船舶日益增多，船舶与冰山发生碰撞事故的可能性也随之增加。船舶一旦与冰山碰撞造成破损，很可能发生漏油事故，影响极地地区的生态环境。因此，为了保证航线的安全性，提高船舶结构的可靠性，需要在船舶结构设计阶段考虑冰载荷的影响。因此，准确模拟船冰碰撞场景，预测碰撞结果，为船舶设计阶段提供数据参考非常重要。

冰的力学性质十分复杂。冰的形成过程高度依赖于环境条件，如海水盐度、温度等，因此不同区域的海冰的性质不同。如在俄罗斯北部，因有大量的河流入海，海冰的种类和性质与北美北极圈的Beaufort海就有很大的不同［1］。从宏观组成上，海冰由固体冰、盐囊、气体和孔隙等组成，其物理性质相当复杂。在微观层面上，冰的性质决定于晶体大小及其结构。粒状冰、柱状冰和不连续冰为三种基本冰晶结构［2］。如果组成海冰的晶体结构不同，或者排列方式不同，海冰的力学性质也会不同。比如多年冰晶体排列无明显方向性，可近似为各向同性材料。一年冰由于其柱状冰的方向性，只能简化为正交异性材料。在宏观方面，冰的厚度、孔隙率等是冰失效条件的重要影响因素，由于冰在其环境中较高的同系温度（Th＞0.8），它的力学行为与应变率有关。当应变率较低时，冰主要表现为延性破坏，软化行为是此破坏模式的最明显的特征。然而，冰在高应变率条件下会表现出明显的脆性破坏，在载荷峰值之后破坏，彻底失去承受载荷的能力。冰强度的最大值出现在两者的过渡区域，应变率≈0.001s-1［3］。所以，在低应变率条件下，冰可近似为非线性的粘弹塑性材料，同时伴有延性失效模式的材料［4］。在高应变率条件下，冰可看作线弹性并脆性失效模式材料。在脆性失效模式下，冰的压缩强度远大于拉伸强度［5］。鉴于冰材料的复杂性，完全模拟其在碰撞过程中的物理变化过程是相当困难的。目前对冰材料的模拟主要集中在冰载荷模型上，重点模拟其压力-面积曲线特性。

许多学者提出了不同的冰材料本构模型。Gagnon［6］根据冰块与船舶模型的实验现象，提出了泡沫模型模拟冰材料本构模型，可有效解释在试验中观测到的冰在碰撞区域的融化现象。Jordaan［7］则从微观层面描述了冰的破碎过程，利用随机概率的方法提出了两种压力-面积曲线描述冰载荷特性。Jebaraj［8］利用有限元的方法模拟船冰碰撞过程，但是其冰材料模型比较简单，需要进一步完善。季顺迎、岳前进［9］则总体介绍了冰的数值模型，针对性的研究分析了渤海海冰的相关性质。本文提出了一种基于弹塑性模拟的冰材料本构模型，并嵌入到LS_DYNA程序，模拟海冰材料特性，应用于船冰碰撞数值仿真计算，进而探讨冰的局部形状对冰的力学行为的影响。

1 冰的弹塑性材料特性模拟

1.1弹塑性材料理论

冰材料模型是影响有限元模拟结果准确性的重要因素之一。但是，由于冰材料的复杂性，难以模拟船冰碰撞过程中冰材料的所有行为特性。因此，目前的研究主要集中在模拟碰撞过程中的冰载荷特性。Ralston［10］研究了冰破碎的屈服条件和塑性变形，为用塑性理论研究冰材料证明了其可行性。本文利用理想弹塑性材料模拟冰的载荷特性，进而研究船冰碰撞中两者的相互作用过程。

理想弹塑性是塑性本构关系的特殊形式之一，其在塑性阶段不产生硬化，即硬化函数为零。在弹性阶段应力应变满足广义胡克定律。图 1为一维条件下的理想弹塑性本构关系，冰材料的本构关系为一维形式在三维空间的泛化。

在弹性阶段，应力应变满足广义胡克定律，如公式（1）所示。

图1　理想弹塑性本构关系示意

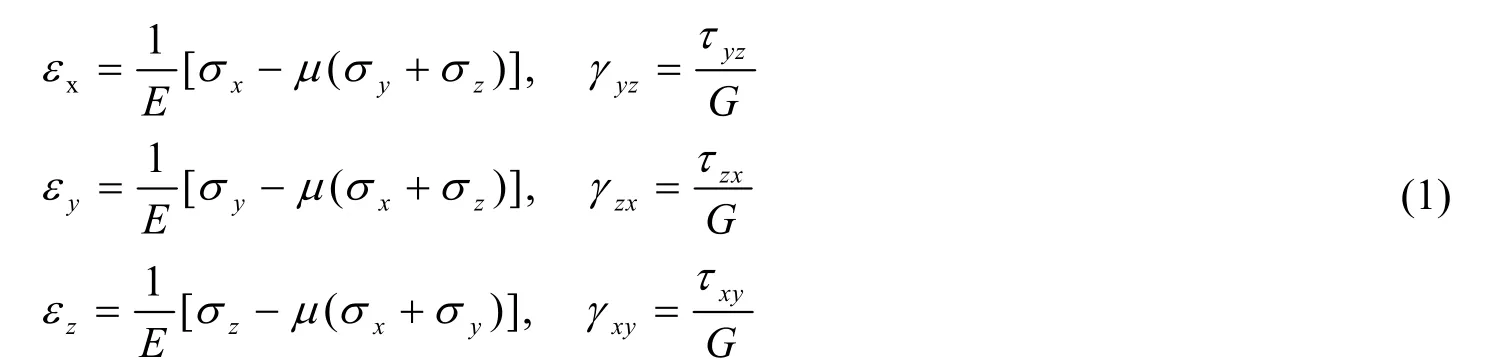
式中：E——弹性模量；μ——Poisson比；G——剪切弹性模量，且）——正应变；）——工程切应变，且

其弹性本构关系增量形式为：

屈服方程是判断弹性状态和塑性状态的准则。因此，一个较为准确的屈服方程对准确模拟冰材料尤为重要。一般情况下，在碰撞过程中，碰撞面积处的冰单元受周围单元的高度限制，处于典型的三向应力状态。Jones［11］和Rist［12］的实验结果表明，对于冰材料，静水压力对屈服状态的影响是不可忽略的。冰的压缩强度随着静水压力的增加而增加。因此采用Tsai-Wu［13］屈服准则，如公式（4）所示，即第二偏应力不变量为静水应力的二次函数。Tsai-Wu 屈服是以300个实验数据为基础提出的，在船冰碰撞研究中被广泛采用。其函数为：

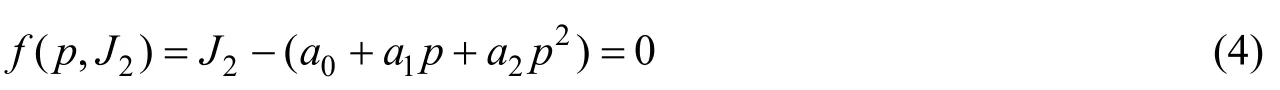
式中：J2——第二偏应力不变量；P——静水应力。a0，a1，a2——分别为常数，表1中所示为常数的取值。本文采用Derradji-Aouattu推荐的取值。

表1　常数取值

提出的理想弹塑性材料在塑性阶段采用增量理论本构关系。根据Drucker公设中的假设，应变分为弹性应变与塑性应变，则应变增量也分为弹性应变增量与塑性应变增量，如公式（5）所示，其中——弹性应变，——塑性应变。

弹性变形规律不因塑性变形而改变，应力仍然符合广义Hooke定律，即

塑性应变增量方向与加载面的外法线方向重合。

式中：dγ——一非负的塑性一致性参数，塑性加载时dγ＞0，中性变载和卸载时dγ=0。

如果采用关联流动法则，φ则为屈服函数，即Tsai-Wu 屈服函数。

所以，塑性阶段的本构关系可表示为式（7）。弹性阶段的应力可用Hook定律求出解析解，塑性阶段的应力由于塑性一致性参数的不确定性，需利用算法求取其数值解。

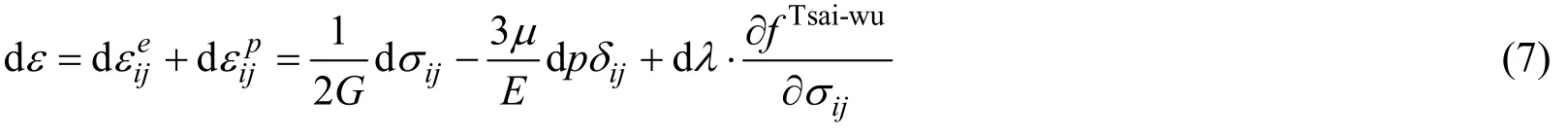
理想弹塑性本构关系的关键问题之一为失效条件的确定。本文采用Zhenhui Liu［14］提出的以等效塑性应变和静水应力为基础的经验失效准则，如公式（8）：

1.2塑性流动理论算法实现

对于塑性单元或弹塑性过渡单元，其应力的计算十分复杂。常用的应力更新积分算法有：显式和隐式图形返回法。表2为不同应力更新积分算法的优缺点比较，本文采取半隐式图形返回法［15］进行迭代求解。

表2　不同本构积分算法比较

根据所提到的基本理论，第n+1步的应力可以表示成公式（9）的形式

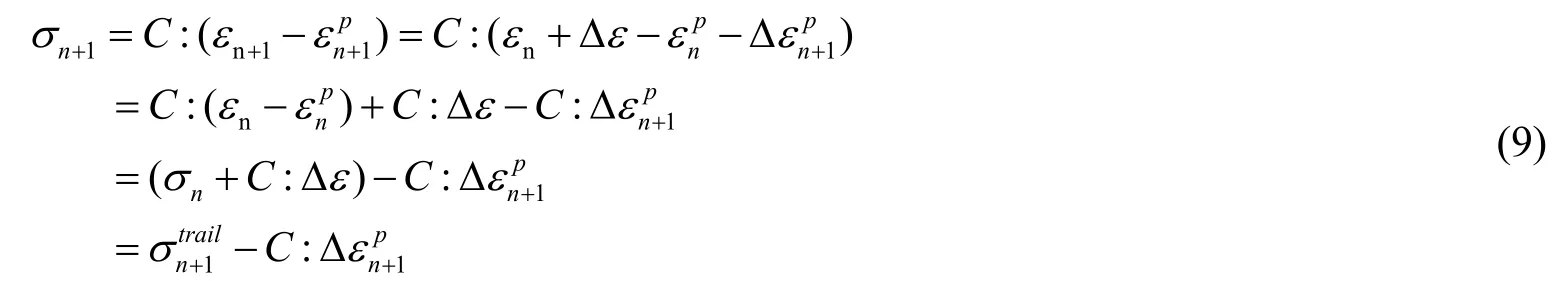
因此可以把半隐式图形返回法分成两步：初始的弹性预测步，以及由于应力对屈服表面产生偏离所需的塑性调整步，如式（10）所示。

同时，此种算法在步骤结束时强化屈服条件，避免了屈服面的漂移，对塑性一致性参数采用隐式，而对塑性流动方向和塑性模量采用显示。积分方法可归结为：

因此程序的第一部分为求解试验应力σtrial，其应力应变关系满足 Hooke定律，随之代入屈服函数进行判别：

如在弹性阶段则σtrial=σ，即试验应力为真实应力。如在塑性计算，则进行塑性修正，使试验应力回到屈服面上，见图2。

图2　图形返回算法几何示意

式中：Eσ——弹性空间； ∂Eσ——弹性空间界面，即屈服曲面；——由εn计算出的试验应力；σn+1——真实应力。

1.3编程过程

步骤1：初始化

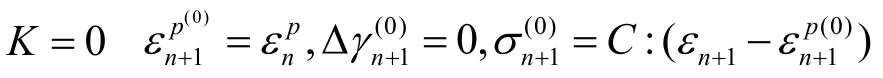
步骤2：计算应力和屈服函数

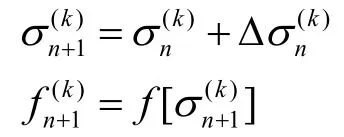
步骤4：计算塑性一致性参数增量

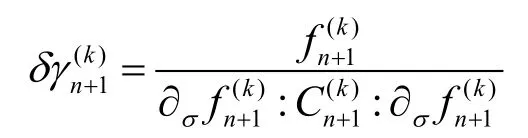
步骤5：更新状态变量和一致性参数

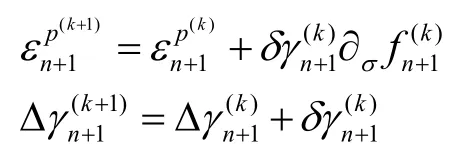
步骤6：令K=K+1利用更新后的塑性应变和一致性参数代入步骤2进行计算。

2 冰材料本构模型验证

首先利用单元测试验证冰单元的材料性质。采用共8个节点1个积分点的单元，其一侧的4个节点固定，另一侧的4个节点施加0.05m/s的速度以压缩单元。图3 （a）、3 （b）为利用单元实验得到的屈服曲线和失效应力。冰单元的屈服方程表现为抛物线型，与“1”中表达一致。屈服应变最小值为0.1，发生在静水应力为50MPa处。一旦应变达到失效应变，单元失效并被删除。图3（c）为改变速度方向进行的拉伸试验得到的截断应力，当拉伸压力达到2MPa之后则不再增加，从而确定了材料的拉伸性能。为与图3（a）、图3（b）中的压缩方向的静水应力区分开，图3（c）中的拉伸方向的静水应力用负值表示。通过与试验结果的比较分析，验证了本文提出的冰材料本构模型的准确性。

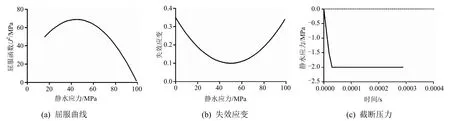
图3　试验曲线分析

以球形冰-钢板计算工况为例，研究冰本构模型失效破碎的相关性质，并验证冰材料本构模型的适用性。球形冰的半径为1m，碰撞速度为1m/s，碰撞时间设定为0.5s。冰的压力-面积曲线是冰力学的基本特性之一，被广泛应用于计算船冰相互作用过程中的冰载荷分析。Masterson［16］提出了这一压力-面积公式，并且被ISO（19906）［17］采用。测定冰在相互作用过程的压力-面积曲线，并与ISO规范进行对照验证，结果如图4（b）所示。由该图可知，两者在碰撞面积＞0.3m2的条件下吻合较好，而船冰碰撞的接触面积一般大于此值，因此本文提出的冰本构模型可较为准确的应用到船冰碰撞数值仿真中。图4（a）为在结束时刻的冰压力云图。在碰撞区域存在高压区和低压区，并且随着时间推进，两者相互转换，高压区的静水应力可达到77.3MPa，低压区的应力在2MPa左右，此静水应力范围与Gagnon的实验数据较为一致。图4（c）为碰撞力-时间曲线，随着碰撞的深入，碰撞力成锯齿形增加。如果冰单元失效，则不再对碰撞贡献力，碰撞力下降，直到一个新的较大的碰撞面积形成，更多单元参与碰撞过程，碰撞力才进一步增加。此锯齿形状为船冰碰撞力曲线的典型形状。

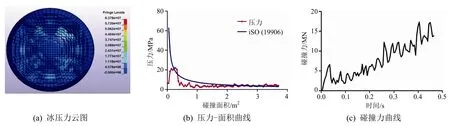
图4　球形冰-钢板碰撞分析

3 利用冰材料本构模型作船冰碰撞数值仿真分析

3.1碰撞场景模型及参数设置

不同的冰局部形状可能导致不同的碰撞场景，构建了5种形状的海冰模型，模型单元与几何尺寸见图5。冰单元采用一个积分点的体单元，大小控制在50mm×50mm×50mm左右。在冰块模型后面加一层与之共享节点的刚体单元，用来模拟冰块其他部分对此局部的作用力，同时给以刚体节点V=2m/s的速度推进冰模型与船侧相撞［18］。碰撞位置选择为船外板的中心位置处。为了节省计算时间，只选取一段船侧模型见图5（6），船舶主尺度见表4。舱段模型长35m，高26m，船侧纵桁布置间隔为900mm，船侧肋板厚21mm，每隔5000mm布置一根。不作针对性的冰区加强。在船侧模型两侧固定位移和转动，用来模拟船舶其他部分对此舱段的边界条件作用。船体结构单元采用Belystchko-Tsay 壳单元，平均大小为225mm。

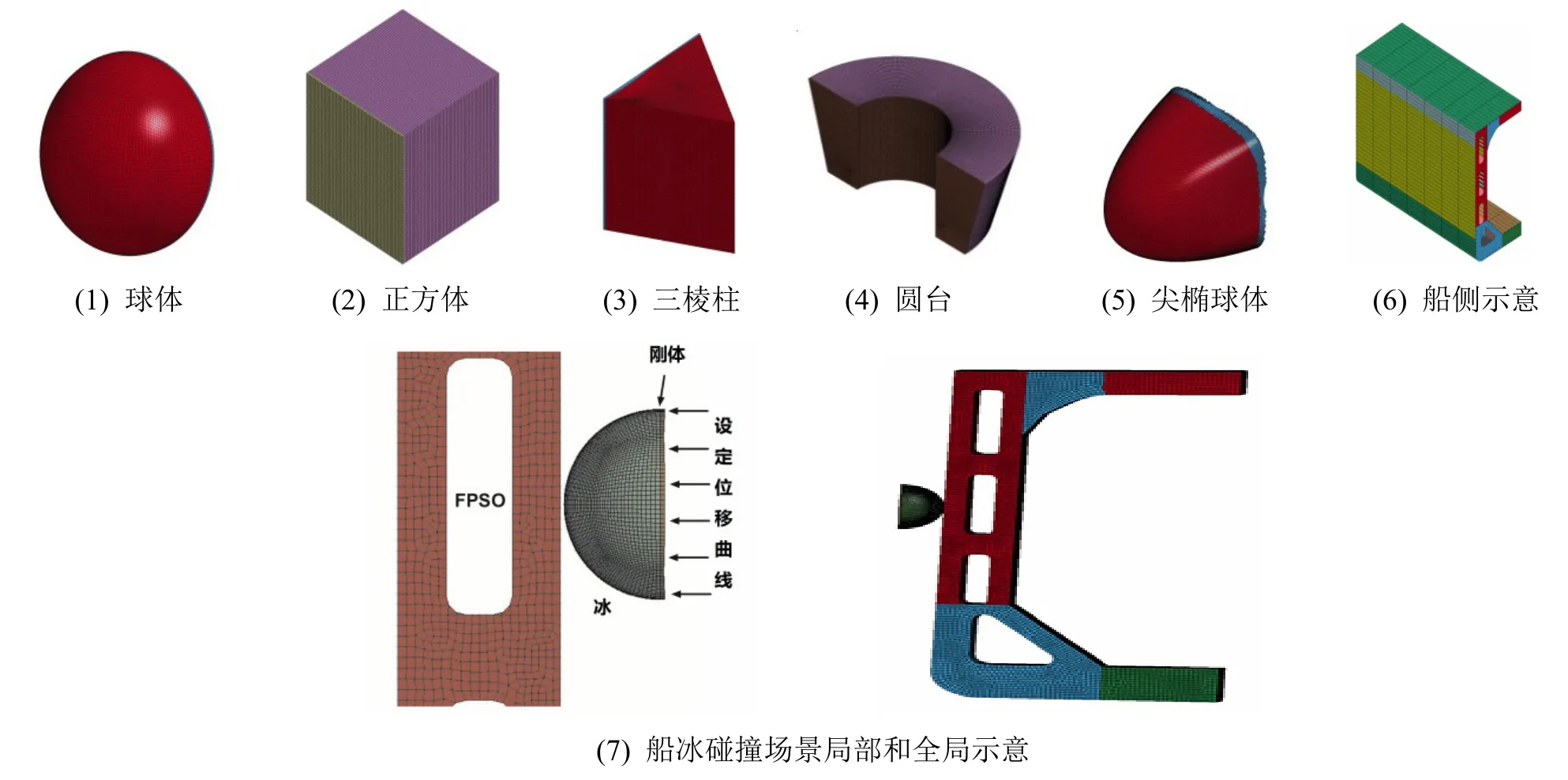
图5　船侧与冰块局部形状模型

表3　冰块模型几何参数 单位：m

表4　船舶主尺度 单位：m

表5　冰与船体的材料参数

3.2计算结果

限于篇幅，选取代表性结果显示碰撞仿真结果。图6和图7分别为三棱柱冰块与球状冰块在船冰碰撞过程中的破碎情况；图8为球体冰块碰撞过程船侧的变形情况及应力云图；图9为不同冰块形状的碰撞力和能量曲线。由图6和图7可知，随着碰撞的持续，三棱柱冰块破碎状况非常明显，大量冰单元失效。相反，球体冰仍保持原始形状，较少冰单元失效删除。可以看出：对于较钝的冰块，船侧为能量耗散的主体，冰内能/总内能在较低水平；对于较为尖锐的冰块，冰块为能量耗散的主体，冰内能/总内能维持在一较高水平（见图9）。相比于其他形状，由于拥有较大的碰撞面积，方形冰的碰撞力和总内能最大，最大碰撞力可达到58.9MN，最大总内能接近70MJ；相对于其他形状，球体冰表现得最为坚硬。船侧外板在碰撞过程中未被穿透，但发生较大的塑性变形，船侧纵桁和船侧纵骨变形也较大，并且在碰撞区域发生断裂现象。

图6　三棱柱冰块t=0.5s和t=1s破碎情况

图7　球状冰块在t=0.5s和t=1s的破碎情况

图8　球体冰碰撞中船侧变形情况与应力分布

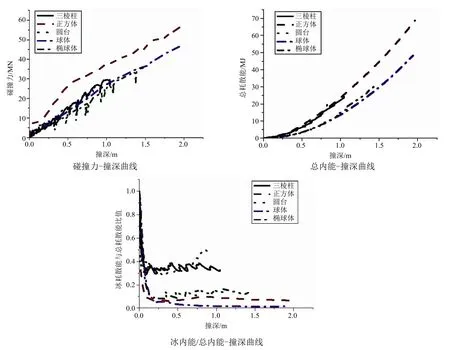
图9　球状冰与三棱柱状冰的碰撞力及能量曲线

4 结 语

提出一个利用理想弹塑性本构关系的冰材料模型，并嵌入到LS_DYNA程序中，应用到船冰碰撞数值仿真中，研究冰块在不同局部形状条件下与船侧碰撞的特性，着重分析在碰撞过程中的碰撞力和能量耗散情况，为船舶在冰载荷作用下的结构设计提供参考。研究得到以下主要结论：

1） 提出的理想弹塑性材料本构模型，可较合理地模拟冰的受挤压失效的行为特性；该模型可以较方便地嵌入到数值仿真程序中；

2） 不同局部形状的冰块在碰撞过程中表现出的力学性质不同；较钝形状的冰块表现近乎刚体，而较尖锐形状的冰块较易破碎，为能量耗散的主体；正方体冰块的碰撞力和总内能最大，因此可以作为最危险的局部形状进行进一步研究；

3） 船侧结构发生较明显的塑性变形，如航行在冰区，需采取一定程度的冰区加强措施。

［1］ Timco G.W.， Weeks W.F.. A review of the engineering properties of sea ice［J］. Cold Regions Science and Technology， 2010. 60 （2）： 107-129.

［2］ 丁德文. 工程海冰学概论［M］. 北京：海洋出版社，1999.

［3］ Schulson E.M.. Brittle failure of ice［J］. Engineering Fracture Mechanics， 2001. 68 （17）： 1839-1887.

［4］ Sodhi D.S.. Crushing failure during ice-structure interaction［J］. Engineering Fracture Mechanics， 2001. 68 （17）： 1889-1921.

［5］ Schwarz， J.， Weeks W.F.. Engineering properties of sea ice［J］. Journal of Glaciology， 1977. 19 （81）.

［6］ Gagnon R.E.. A numerical model of ice crushing using a foam analogue［J］. Cold Regions Science and Technology， 2011. 65（3）：335-350.

［7］ Jordaan I.J.. Mechanics of ice-structure interaction［J］. Engineering Fracture Mechanics， 2001. 68（17-18）： 1923-1960.

［8］ Jebaraj C.， et al.. Finite element analysis of ship/ice interaction［J］. Computers & Structures， 1992. 43（2）： 205-221.

［9］ 季顺迎，岳前进. 工程海冰数值模型及应用［M］. 北京：科学出版社， 2011.

［10］ Ralston T.D.. Yield and plastic deformation in ice crushing failure［C］//ICSI/AIDJEX Symposium on Sea Ice--Processes and Models， Seattle， Washington. 1977.

［11］ Jones S.J.. The confined compressive strength of polycrystalline ice［J］. Journal of Glaciology， 1982. 28： 171-177.

［12］ Rist M.A.， Murrell S. Ice triaxial deforntation and fracture［J］. Journal of Glaciology， 1994. 40（135）.

［13］ Derradji-Aouat A.. A unified failure envelope for isotropic fresh water ice and iceberg ice［C］//Proceedings of ETCE/OMAE Joint Conference Energy for the New Millenium， 2000.

［14］ Liu Z.， Amdahl J.， Løset S. Plasticity based material modelling of ice and its application to ship-iceberg impacts［J］. Cold Regions Science and Technology， 2011. 65（3）： 326-334.

［15］ Simof J.C.， Hughes T. Computational inelasticity［M］. 2008.

［16］ Masterson D.M.， et al. A revised ice pressure-area curve. in Proceedings［C］//Nineteenth International Conf. on Port and Ocean Engineering under Arctic Conditions， Dalian， China. 2007.

［17］ International S.O.. Petroleum and natural gas industries — arctic offshore structures［Z］， in ISO TC 67/SC 7/WG 8. 2010：Geneva， Switzerland. 434.

［18］ Storheim M.， et al. Iceberg shape sensitivity in ship impact assessment in view of existing material models［C］//ASME 2012 31stInternational Conference on Ocean， Offshore and Arctic Engineering. Rio de Janeiro， Brazil. 2012.

A New Constitutive Model of Ice Material for Ship-ice Interaction based on Ideal Elasto-plastic Property

HU Zhi-qiang1，2，GAO Yan1，YAO Qi1
（1. State Key Laboratory of Ocean Engineering， Shanghai Jiao Tong University， Shanghai 200240；2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai Jiao Tong University， Shanghai 200240）

Ship-ice interaction is currently one of the hot topics of the ship collision research， and the modeling of ice material is one of the key issues in ship-ice collision research. A constitutive model of ice material for ship-ice interaction based on the ideal elastic-plastic property is proposed in this paper， which calculate the element stress in plastic stage with the semi-implicit return mapping algorithm and describes the ice mechanical behavior with the Tsai-Wu yield criterion and empirical failure formula. Secondary development function is used to incorporate the ice material model into LS_DYNA program to validate the accuracy and applicability of the model. In accordance with the scenarios of collisions between a ship and ice blocks of different shapes， the study compares and analyzes the collision force， energy dissipation and etc. to discuss the influence of the ice shape on collision scenarios. The result shows that the pressure of the ice material model agrees well with existing standards in case the contact surface is large. The interaction processes of the ship-ice collision are different with different ice shapes. The blunt-shaped ice performs like a rigid body， while sharp-shaped ice is easy to be broken.

ship-ice collision； elastic-plastic material； constitutive model； influence of iceberg shape； numerical simulation

U661.7

A

2095-4069 （2016） 01-0065-09

10.14056/j.cnki.naoe.2016.01.013

2015-08-31

国家自然科学基金重点项目（51239007）。

胡志强，男，副教授，1975年生。2008年上海交通大学船舶及海洋结构物设计制造专业获博士学位，现于上海交通大学船舶海洋与建筑工程学院工作。