福建柏人工林工艺成熟的研究
周宗哲
(福建省安溪白濑国有林场,福建 安溪 362411)
福建柏人工林工艺成熟的研究
周宗哲
(福建省安溪白濑国有林场,福建 安溪 362411)
利用标准地和伐区调查设计材料,选择理查德方程建立福建柏人工林林分因子模型,采用联合估计方法建立林分材种出材率模型;在此基础上,探讨不同立地条件下经济材总量以及各分量(大原木、中原木、小原木)的工艺成熟,并兼顾数量成熟。结果表明:蓄积量、经济材总量及各分量的成熟龄与立地质量密切相关,立地质量越好,成熟龄到来的时间越早,反之亦然,但并非各种立地均适合于培育中原木和大原木。对于福建柏人工林,若要培育中、大原木,至少要在地位指数16 m以上的林地上造林,而14 m指数以下的林地则只能用于培育小原木。研究结果可为福建柏人工林主伐年龄的确定提供参考。
福建柏;工艺成熟;数量成熟;材种出材率
森林生长发育过程中达到最符合经营目的的状态称为森林成熟,按林种有用材林、薪炭林、经济林、防护林成熟等,其中用材林和薪炭林的成熟是确定主伐年龄的主要依据,应用最为普遍,对其研究也最多。主要原因是用材林和薪炭林与农业上的农作物或果树的成熟相比,最大区别是没有明显的成熟特征,且与森林经营目标有关而呈现多样化的森林成熟,从而吸引了不少学者的关注并开展研究,其目的是为确定主伐年龄提供依据。对于薪炭林,在持续经营的前提下,以追求数量最多为主要目的,衡量森林成熟的主要标志是材积平均生长量达到最大值,此时的年龄为数量成熟龄。而对于用材林,既要考虑森林经营中的材积收获数量最多即数量成熟龄,还需满足目的材种年均生长量最大,森林生长达此状态时通常称为工艺成熟,此时的年龄为工艺成熟龄。由于社会需求的多样化,使得目的材种按其小头去皮直径的不同有多种类型。与此相对应,同一立地条件下因目的材种不同而有不同的工艺成熟龄。探讨同一树种不同立地条件下的森林工艺成熟,对于合理采伐取得尽可能大的经济效益有其重要的理论和实践意义。
福建柏为福建省主要造林树种,亦是国家二级保护的特有珍贵用材树种,因最先在福建省采到标本而得名。自1955年以来,福建省先后在30多个县(市)营造了福建柏人工林,结果表明:福建柏对立地条件要求比杉木低,生长速度比同等条件下的杉木快,造林和经营成本也比杉木低,木材物理力学性能比杉木好。因此,在大力提倡多树种造林的今天,福建柏就成为新兴的、较有发展前途的优良用材树种之一。但是,林业生产上多年来一直未对福建柏人工林的工艺成熟进行系统的研究,现有的福建柏人工林技术经营体系尚不成熟,显然,这种状况十分不利于福建柏人工林的科学经营管理。鉴于此,本文对福建柏人工林的工艺成熟并兼顾数量成熟进行研究,为其主伐年龄的确定和提高森林经营水平提供参考。
1 材料来源
在安溪县白濑国有林场及泉州其他国有林场,分别不同林龄、立地、密度且生长正常的福建柏人工林林分中,采取典型选样原则并结合伐区设计,收集调查173块标准地,每块标准地面积为667 m2,按森林资源调查技术规定要求测算蓄积量、出材量及相关林分调查因子。经整理汇总,得到标准地各调查因子分布范围:年龄8~42 a,平均胸径6.2~28.5 cm,平均高4.1~24.4 m,优势高5.6~26.1 m,密度720~3282株·hm-2,蓄积量16.4~461.5 m3·hm-2。
2 林分因子模型构建
利用所采集的标准地数据,建立林分主要调查因子模型和出材率模型,分析测算不同立地下福建柏人工林工艺成熟,并兼顾数量成熟。
2.1 林分因子模型
反映林分特征的基本因子是林分平均胸径、平均高和单位面积蓄积量,尤以蓄积量最为重要。在未受干扰且正常生长的林分中,林分平均胸径、平均高和单位面积蓄积量随年龄增加而不断增加,其生长过程呈“S”型生长曲线,描述这种曲线的生长方程为数不少,其中以理查德方程应用最广。主要原因是该方程适用性强、准确度高且方程中的参数有一定的生物学意义,基于此,本文选择理查德方程构建福建柏人工林地位指数曲线模型,并将地位指数引入理查德方程,建立不同立地的福建柏人工林林分平均胸径、平均高和单位面积蓄积量生长模型,具体形式如下:
地位指数曲线模型:Hu=4.3896SI×[1-exp(-0.0069T)]0.7241
(1)
平均胸径模型:Dg=12.7492SI0.37[1-exp(-0.001146SI0.902T)]0.6166,R2=0.9726
(2)
平均高模型:Hp=11.7919SI0.2594[1-exp(-0.003273SI1.0508T)]1.441,R2=0.9875
(3)
蓄积量模型:M=6.2277SI1.5364[1-exp(-0.01234SI0.5339T)]1.9314,R2=0.9849
(4)
式中:Hu为优势高;Dg为平均胸径;Hp为平均高;M为蓄积量;SI为地位指数;R2为相关指数。
2.2 林分材种出材率模型
林分材种可分为经济材、薪材和废材3个部分,本文着重分析经济材的工艺成熟并兼顾蓄积平均生长量最大的数量成熟。在经济材中,目的材种按其小头去皮直径(dn)及材长(L)分为大原木(dn≥26 cm,L≥2 m)、中原木(dn=20~26 cm,L≥2 m)、小原木(dn=6~20 cm,L≥2 m)、短材(dn≥14 cm,L=0.4~1.8 m)和小材(dn=4~14 cm,L=1.0~4.8 m),短材和小材合并为短小材。
2.2.1 林分材种出材率变化规律分析 分析研究表明:林分的经济材在平均胸径较小时出材率较低,随着平均胸径的增大而提高,当平均胸径达到一定程度时,上升的速度减缓且趋于平稳。林分大原木出材率随着平均树高和胸径的不断增大而提高,开始的增长速度快,以后增加的速度变慢最终也趋于平稳。中原木出材率随着平均胸径的增加而增加,增长的幅度较大,在某一平均胸径时达到最大值,以后随着大原木的出现而开始随平均胸径的增大而不断下降;小原木出材率变化规律与中原木基本一致,先随平均胸径的增加而上升,达到最大值后由于出现了中原木而随着平均胸径不断增大而逐渐减缓直至平稳。中原木和小原木出材率按平均胸径的分布均呈中间高两边低的非对称山状曲线。短小材出材率变化规律与大原木相反,随着平均胸径增大而不断减小,呈反“J”型曲线。
林分材种出材率各分量满足代数和关系,若以经济材为分母,大原木、中原木、小原木和短小材出材率比例合计应为100%。林分材种出材率建模的常规方法是各分量模型独立拟合,这种建模方法没有考虑大原木、中原木、小原木和短小材出材率之间存在的代数和关系。虽然独立拟合建模能够通过对模型结构的合理设计来满足各材种出材率模型估计精度的要求,但这种建模方法存在着一个严重的问题是,独立建立的各材种出材率模型与总量即经济材出材率模型不兼容,且各材种出材率估计值之和与以经济材为分母作为总量的100%必定不完全相等。为克服上述问题,满足材种出材率各分量占总量比例之和为100%,本文采用联合估计方法建立各分量出材率模型系统。
2.2.2 林分材种出材率模型构建 在森林调查中,胸径和树高是最基本的直接测树因子,材积、材种出材率通常由这2个因子推算而得。同理,以林分为整体,采用平均胸径、平均高为辅助变量建立林分材种出材率模型是首选作法。为简化模型结构,取平均胸径D、平均高H的组合(X=D2H/100)作为辅助变量建立林分材种出材率模型。前述林分材种结构分析表明,材种出材率在不同分量上的分配比例随平均胸径增大而呈有规律的变化。经济材、大原木占总林分蓄积量比例随着平均胸径增长而逐渐增大,达到一定程度后趋于平稳;短小材所占比例却随平均胸径的增大而减小最终也趋于平稳;中原木和小原木先随平均胸径增长而逐渐增大,达到一定程度后又随平均胸径的增大而减小,呈中间高两边低的山状曲线分布。基于此,用如下2种形式的非线性方程作为林分各材种出材率模型:
f(x)=aexp(b/X)
(5)
f(x)=aXbexp(cX)
(6)
式中:a、b、c分别为模型参数。(5)式适用于经济材、大原木(b<0)和短小材(b>0),(6)式适用于中原木和小原木(c<0)。
采用非线性方程联合估计的方法构建相容性林分材种出材率模型系统的基本原理是:设f0(x)、f1(x)、f2(x)、f3(x)、f4(x)分别代表经济材、大原木、中原木、小原木、短小材出材率模型,P0、P1、P2、P3、P4、分别为经济材、大原木、中原木、小原木、短小材出材率理论值。首先建立经济材出材率模型,以此为基础作为分母,以各分量满足100%进行控制,则有:
(7)
(8)
(9)
(10)
式中:W1(x)=f2(x)/f1(x),W2(x)=f3(x)/f1(x),W3(x)=f4(x)/f1(x),将(5)、(6)式代入,可得:
(11)
(12)
W3(x)=b31×exp[(b32-b33)/X]
(13)
式中:b11、b12、b13、b14、b21、b22、b23、b24b31、b32、b33均为模型参数。
上述材种出材率模型为非线性方程,通常的估计方法是最小二乘法。当估计独立模型参数时,其准则是残差平方和最小。与此相对应,对于相容性林分材种出材率模型系统,在估计参数时必须同时满足各分量估测误差最小。但是,不同材种出材率的数量差异较大,为取得较理想的拟合效果,本次用加权最小二乘法联合估计各材种出材率模型参数,具体准则如下:
(14)

权重Ci可看成是联合估计中对各个材种出材率模型的重视程度,在经济材中,大原木、中原木、小原木权重均取值为0.3,短小材所占比例最少,取值为0.1。用加权最小二乘法建立目标函数,用联合估计的方法确定参数,用智能算法中的免疫进化算法[3-5],建模结果如下:
P0=83.4965×exp(-3.23144/X),R2=0.9423
(15)
W1(x)=0.0009464X1.58011×exp(-0.01195X-97.45214/X),R2=0.9027
(16)
W2(x)=2.0485278X-0.61121×exp(0.002638X-97.45214/X),R2=0.9052
(17)
W3(x)=0.010973×exp[(22.42295-97.45214)/X],R2=0.9223
(18)
将(15)~(18)式代入(7)~(10)式,即可求出各材种出材率,其中,经济材出材率由(15)式确定。
3 工艺成熟的分析
给定地位指数,由林分因子模型求出不同年龄时的林分平均胸径、平均高、蓄积量和出材率,并进一步求出各材种出材量及相应的平均生长量,以16 m指数级为例,计算结果见表1。
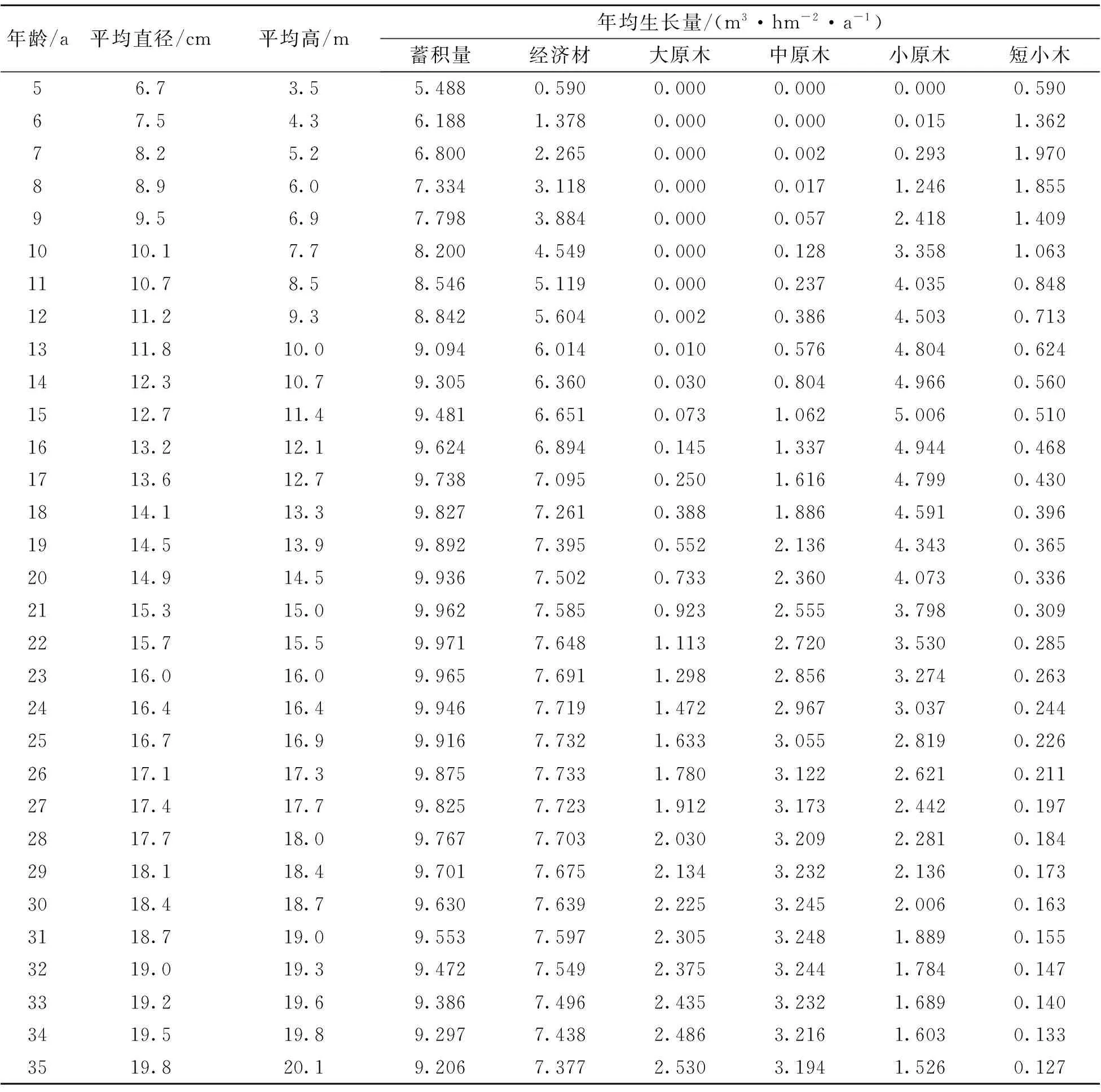
表1 福建柏人工林成熟龄计算结果(16指数级)
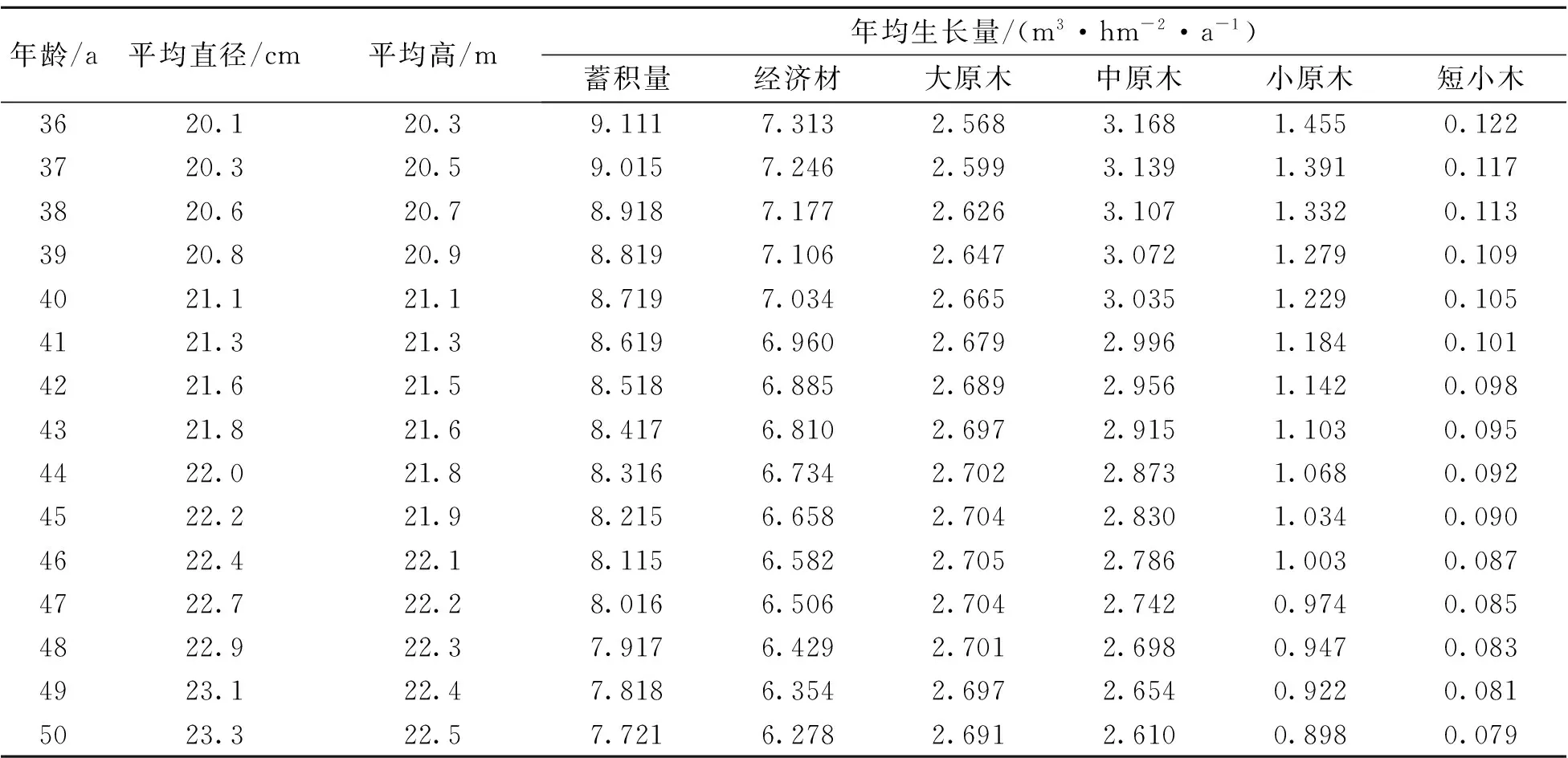
表1(续)
用材林经营中,材积年均生长量达到最多时的年龄称为数量成熟龄,推而广之,各材种年均生长量最大时的年龄为相应材种的工艺成熟龄。由表1可知,无论是蓄积量还是出材量,年均生长量均随年龄增加而上升,至最大值后随年龄增加而下降,图1直观体现了中间高两边低的非对称山状曲线生长变化过程。
福建柏人工林16指数级林分蓄积量和各材种出材量达到最大值的时间并不一致,以短小木达到最大值的时间最早,仅7 a,此即短小木的工艺成熟龄。但是,以短小木为目的材种培育用材林是没有意义的,通常只作为用材林采伐时的附属产品加以利用,以期提高木材利用率。福建柏人工林16指数级材积平均生长量达到最大值的年龄为22 a,此年龄为数量成熟龄,意味着在持续经营的前提下,在此年龄采伐平均每年获得的材积收获量最大,蓄积量年均生长量可达9.971 m3·hm-2,但与目的材种无关。若以经济材出材量平均生长量最大值为衡量标准,则对应的年龄为26 a,年均收获量可达7.733 m3·hm-2,时间上迟于数量成熟龄。当目的材种分别为小原木、中原木、大原木时,对应的工艺成熟龄分别为15、31、46 a,相应的年均收获量为5.006、3.248、2.705 m3·hm-2。显然,随着材种规格即小头去皮直径的提高,工艺成熟龄不断往后推移,年均收获量则依次下降。材种出材量各分量中,小原木工艺成熟龄比经济材的成熟龄更早,也早于数量成熟龄,若以小原木工艺成熟龄作为主伐年龄,经济材的年均收获量为6.651 m3·hm-2,明显低于以经济材为目的材种的工艺成熟龄所对应的年均收获量7.733 m3·hm-2。而以中原木工艺成熟龄作为主伐年龄,经济材的年均收获量为7.597 m3·hm-2,略低于经济材的最大年均收获量,二者很接近。因此,在地位指数16 m的林地上培育福建柏人工林中原木,经济材和目的材种均可取得尽可能大的收获量,是一种适宜的经营目标。当然,对于16指数级的福建柏人工林,可以培育出大原木,但主伐时间要在40 a以后,且经济材的年均收获量也明显下降。
以上仅就福建柏人工林16指数级数量成熟及工艺成熟进行初步分析,各种立地的数量成熟龄、工艺成熟龄以及对应的材积年均生长量见表2。由于小径木仅仅是采伐的附属产品,不能作为森林经营的目标,故不作进一步讨论。

表2 福建柏人工林成熟龄及年均生长量
*:地位指数单位为m;成熟龄单位为a;生长量单位为m3·hm-2·a-1。
各种立地条件下福建柏人工林成熟龄及对应的年均生长量共同变化规律是:随地位指数的提高,成熟龄不断提前,年均生长量不断上升,蓄积量的成熟龄均早于经济材的成熟龄。在各地位指数级经济材各分量中,小原木最早达到工艺成熟且均早于经济材成熟龄;其次是中原木,但都迟于蓄积量和经济材的成熟龄;最后到达工艺成熟的为大原木,除20 m指数级外,工艺成熟龄都在40 a以后。而对于低指数级如8、10、12 m,60 a以后未达到工艺成熟,可以认为,低指数级林地基本上不存在大原木的工艺成熟龄,亦即难以或者无法培育大原木,甚至无法培育中原木,如8 m指数级。
4 结论和讨论
材种出材量总量及各分量之间存在相互制约的关系,随林分平均胸径增加呈现复杂的变化过程。本文采用联合估计方法建立各分量出材率模型系统,从理论上满足了材种出材率各分量占总量比例之和为100%的代数和关系,为材种出材率模型的研制提供了依据。
工艺成熟属于数量成熟的范畴,可看作是数量成熟的特殊情况。研究表明:蓄积量、经济材总量及各分量的成熟龄与立地质量密切相关,立地质量越好,成熟龄到来的时间越早,反之亦然,但并非各种立地均适合于培育中原木和大原木。对于福建柏人工林,若要培育中、大原木,至少要在地位指数16 m以上的林地上造林,而14 m指数级以下的林地则只能用于培育小原木。
森林成熟龄是一个年均生长量最大的以年为单位的具体数量概念,分析测算表明:在森林成熟龄一定年限范围内,各年的年均生长量与最大年均生长量差异并不显著,这就意味着在一定年限范围内采伐,平均每年所获得的材积收获量并无明显差别。因此,以一定年限范围为基准期表示森林成熟,即用森林成熟期代替森林成熟龄来描述森林的成熟状态,并据以确定主伐年龄,或许在实践上更切合实际且便于操作。
森林工艺成熟是针对某一目的材种而言,目的材种的年均生长量最大,并不代表经济材总量及其他各分量也最大。用材林经营的目标是尽可能获最大的经济效益,因此,作为确定主伐年龄主要依据之一的森林工艺成熟,必须兼顾经济材总量及分量,更深入的分析是要进行经济效益测算,即研究森林的经济成熟。有待进一步深入探讨。
[1]亢新刚.森林经理学[M].3版.北京:中国林业出版社,2006.
[2]孟宪宇.测树学[M].3版.北京:中国林业出版社,2006:44-71.
[3]江希钿,庄晨辉,陈信旺,等.免疫进化算法在建立地位指数曲线模型中的的应用[J].生物数学学报,2007(3):515-519.
[4]施恭明,陈绍玲,江希钿,等.基于免疫进化算法的投影寻踪森林生态功能评价模型[J].福建林学院学报,2013,33(2):142-145.
[5]李晓景,江传阳,江希钿,等.闽北天然阔叶林林分材种结构分析及出材率模型[J].福建林学院学报,2013(2):137-141.
[6]池上评,陈金章,江传阳,等.基于间隔期的福建柏人工林动态生长模型及应用[J].福建林学院学报,2014,34(4):304-308.
Study on the Technical Mature ofFokieniahodginsiiPlantation
ZHOU Zongzhe
(AnxiBailaiNationalForestFarm,Anxi362411,Fujian,China)
Using the sample plot and felling area survey and design data,the stand factor model ofFokieniahodginsiiplantation was established by choosing Richard equation,and the stand timber outturn percentage model was established by adopting the joint estimation method.Based on this study,the technical mature of total economic timber and each grades (large log,moderate log,small log) under different site conditions was analyzed with considering quantitative mature.The results showed the mature age of the volume,total economy timber and each grades had close relationship with the site quality;the better the site quality was,the earlier the mature age would came;and vice versa,but not all site conditions were suitable for cultivating moderate and big log;for the moderate and big log cultivation ofF.hodginsiiplantation,at least the site index 16 m should be adopted;it was for the small log that under the site index 14 m.The study could provides references for the final felling age determination ofF.hodginsiiplantation.
Fokieniahodginsii;technical mature;quantitative mature;timber outturn percentage
10.13428/j.cnki.fjlk.2016.04.033
2015-12-21
福建省自然科学基金资助项目(B0010019)
周宗哲(1971—),男,福建德化人,福建省安溪白濑国有林场高级工程师,从事林木良种选育和森林经营研究。E-mail:zzz23407125@126.com。
S791.43
A
1002-7351(2016)04-0153-06

