基于倒立摆的智能控制课程教学案例设计*
魏利胜, 吴 旭, 郭兴众
(安徽工程大学电气工程学院,安徽 芜湖 241000)
基于倒立摆的智能控制课程教学案例设计*
魏利胜, 吴旭, 郭兴众
(安徽工程大学电气工程学院,安徽 芜湖 241000)
为贯彻落实国家卓越工程师教育培养计划,提高智能控制研究生课程教学质量,将案例教学引入到整个教学体系中.通过对倒立摆系统的智能控制策略分析和科研实践,结合智能控制理论教学要求,设计一种基于特征模型的灰预测黄金分割控制器教学案例,取得了良好的效果.既较好完成了智能控制教学大纲要求,也有效提高了学生解决和研究实际问题的能力.课堂教学效果表明,该案例教学作为一种教学辅助手段产生了有益的影响.
智能控制;案例教学;倒立摆;灰预测
引言
智能控制作为控制科学与工程专业课程体系中的核心课程之一,要求学生能熟练掌握基本智能控制方法,为实际工程应用奠定一定的基础[1].然而,当前智能控制课程的教学明显存在课堂教学与实践应用相互脱节的问题.因此,亟需引入创新型教学方法,对课程体系、教学内容、教学手段等进行全方位改革.
案例教学法是一种启发式教学方法,授课教师根据课程教学目标及要求,通过安排一些具体案例,有针对性地引导学生参与思考、分析和讨论,从而培养学生分析和解决实际工程问题能力的教学方法[2,3];案例可以来源于科学研究,且具备一定的代表性[4].通过调研发现,目前国内高校尚未建立一套完整而规范的智能控制课程教学案例库,也较少开展智能控制课程案例教学方法的研究.
考虑到我校控制科学与工程学科作为安徽省教育厅重点建设学科,该专业也被确定为博士点立项建设专业,如何通过课程教学改革来提高教学质量,充分借鉴案例教学法的教育理念,提高学生的创新技能、实践技能,创建适应新形式发展需要的智能控制课程教学体系,是我校授课老师所面临和亟待解决的问题.
倒立摆系统是一个非线性、绝对不稳定的复杂系统,为控制理论的实验提供了一个良好的实验平台,可有效验证各类控制策略和方法的好坏.因此,在倒立摆系统控制方面的研究受到了许多学者的关注[5].为此,本文针对智能控制课程基于倒立摆系统设计了一种基于特征模型的灰预测黄金分割控制策略实践教学案例,期望能为其他相关课程的教学提供参考.
1 倒立摆系统数学模型
由于倒立摆系统本身是自不稳定的系统,实验建模存在一定的困难.但为了分析和处理问题的方便,通过一些假设(如:摆杆在运动中是规则的不变形的刚体;齿形带轮和齿形皮带之间无相互滑动,齿形带无拉长现象等),从而忽略了系统中的一些次要的因素后,并在一定的范围内进行线性化处理,倒立摆系统就是一个典型的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程.其结构如图1所示.图1中,x表示小车移动距离,θ表示摆杆与垂直向上方向的夹角,并令φ表示摆杆与垂直向下方向的夹角,则φ=π+θ,M表示小车质量,m表示摆杆质量,l表示摆杆转动轴心到质心的长度,J表示摆杆的转动惯量,u表示对小车外力的作用(输入).以小车前进方向为正方向,顺时针作为摆杆摆动的正方向.现分析小车的受力情况,如图2所示.
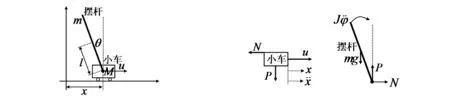
图1 倒立摆系统结构图 图2 小车和摆杆受力分析图
首先,对于小车水平方向有:
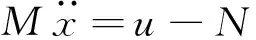
(1)
对于摆杆水平方向有:
(2)
将式(2)代入式(1)中,可知:
(3)
同理,对摆杆垂直方向有:
(4)
则对于倒立摆系统,有如下力矩平衡方程:
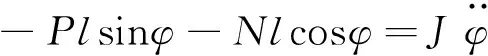
(5)
将式(2)、式(4) 与式(5)合并,则:
(6)
由于φ=π+θ,所以sinφ=-sinθ,cosφ=-cosθ,可得:
(7)
当摆杆与小车垂直时,倒立摆系统平衡,此时θ相对来说比较小,接近0弧度,则可以利用如下近似线性关系:
(8)
将式(8)代入式(7)中,系统运动方程可以简化如下:
(9)
则:
(10)
即:
(11)
令q=(J+ml2)·(M+m)-m2l2,可得:
(12)
2 基于特征模型的灰预测黄金分割控制器
基于特征模型的灰预测黄金分割控制器结构如图3所示.其思路是在原有黄金分割自适应控制器结构的基础上,利用特征模型对系统进行辨识,并在反馈回路构建灰色预测器,从而对网络控制系统的控制量进行超前控制,减少网络随机时延对网络控制系统控制系能的影响.

图3 基于特征模型的灰预测黄金分割控制器结构图

2.1特征模型建立
所谓的特征建模,就是对被控系统建模时既要考虑动力学特征,同时也要结合对象控制性能和环境特征的要求,对未知参数、高阶线性定常系统以及一类非线性系统的控制具有良好的效果.对于相同的输入,特征模型的输出与实际对象的输出是等价的,且系统稳定后,两者相等.常用特征模型如下式表示:
y(k+1)=f1(k)y(k)+f2(k)y(k-1)+g0(k)u(k)+g1(k)u(k-1)
(13)
式中,fi(k),gi(k)为慢时变系数,如果被控制对象无积分项且无重根项,f1(k),f2(k)的最大取值范围分别为:f1(k)∈(1,2],f2(k)∈[-1,10),且在系统等效静态增益D0≤2时,g0(k),g1(k)远远小于1;如果有积分项、有重根项,f1(k)小于并接近2,f2(k)大于且接近-1.为此,需要对倒立摆进行特征模型构建,如下:
设
h(0,0,0,0)=0
(14)
可知:

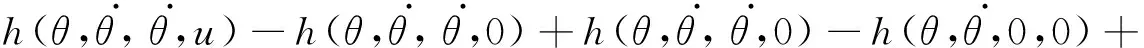
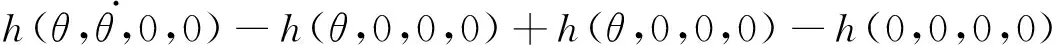
(15)
根据中值定理可得:
(16)
式中,0 (17) 对式(17)进行微分处理: (18) 离散化后代入式(13)可知: v(k)=[ω(k)-ω(k-1)]Δt+ω(k)Δt2. 整理可得到倒立摆系统的特征模型如下: θ(k+1)=f1(k)θ(k)+f2(k)θ(k-1)+g0(k)u(k)+g1(k)u(k-1) (19) 式中: f1(k)=2-[1+2α1(k)-α1(k-1)]Δt+α1(k)Δt2+δ(k)θ(k), f2(k)=-1+Δt-α1(k)Δt+δ(k)θ(k-1), g0(k)=[β1(k)-β1(k-1)]Δt+β1(k)Δt2+δ(k)u(k), g1(k)=-β1(k)Δt+δ(k)u(k-1), 2.2灰预测黄金分割控制器设计 黄金分割控制方法其主要思想就是在设计控制器时引入黄金分割比,即把直线l分成l1和l2两个部分,且满足l1/l2=0.382/0.618的关系.与传统控制方法相比较,黄金分割控制既有特征模型无需建立被控对象精确数学模型的优点,又能在系统的过渡阶段,设计参数未收敛的情况下保证其闭环的稳定性.当二阶被控对象或者高阶可以化为二阶的被控对象利用黄金分割法进行控制时,其黄金分割控制器的控制律设计如下: (20) 为了减少各种不确定性对倒立摆控制性能的影响,进一步引入灰色预测器,并根据系统输出误差调整预测步长,灰色预测模型选用传统GM(1,1)模型.同时,假设误差参考值emin,emax,若误差大于emax,选择负的预测步长,达到增加控制量,并减少过渡响应时间的效果.若误差小于emin,选择较大的正的预测步长,从而达到减小控制量,降低甚至消除超调的效果.其余的误差值,则选择较小的正的预测步长.预测步长调节具体如下: (21) 式中,p1<0 (22) 则可得倒立摆系统实际控制输出预测值为: (23) 则误差预测值为: (24) 案例教学中选用固高科技有限公司的单级倒立摆系统,其中:小车质量为1.096kg,摆杆质量为0.109kg,摆杆转动轴心到质心的长度等于0.25m,摆杆的转动惯量为0.1kg·m2,采样周期设为Δt=0.02 s,则可知该倒立摆特征模型参数估计的范围为: f1∈(1.937,2.065),f2∈(-1.013,-0.987) g0,g1≤1 本方法中灰色预测器的预测步长取: 教学过程中要求采用基于特征模型的灰预测黄金分割控制策略与传统PID控制策略进行对比实验.本机控制时结果如图4所示. 图4 本机控制结果图 为满足部分学生的科学研究兴趣,同时增加实验的可拓展性,可对实验对象采用局域网环境下进行控制,结果如图5所示. 图5 局域网控制结果图 两组实验分别所对应的特征模型参数见表1. 表1 特征模型参数表 从实验结果可以发现本文的所采用的案例方法控制效果要优于传统的PID控制策略,而且在两种不同实验条件下,特征模型参数在线辨识结果基本相同,可见本文所提出的方法可行、有效,能较好帮助学生更深刻地理解智能控制,极大地激发了创新性学习的热情.实践效果证明这是一个很好的教学案例,可以较全面地锻炼学生的科研实践能力,这种教学内容与教学模式的改革对促进智能控制课程教学质量提高、培养国际创新型人才具有重要意义. 智能控制课程作为控制科学与工程类研究生专业核心课程,其教学质量影响学生的就业及在该专业方向上的发展.因此,我们在研究生智能控制理论教学的基础上,引入案例教学,对于研究生知识结构的拓宽、科研能力的提升都起到了非常重要的作用.教学案例不仅满足了学生的感官需求,同时加快了学生的理解速度,提升了学生的课堂积极性,对课程教学质量提高起到了积极推动的作用[6,7].该案例本身只为“智能控制”研究生课程教学而设计的,但是该案例设计理念和实施,可以为其他课程教学提供有益的参考. [1]魏利胜, 郭兴众. 工程教育理念下的智能控制课程教学策略探讨[J]. 中国电力教育, 2014, 318(23): 29-30. [2]诸葛霞, 袁红星, 孔中华, 等. 信号与系统课程中数字图像处理教学案例研究[J]. 宁波工程学院学报, 2014, 26(4):79-82. [3]王晓兰, 李恒杰. 线性系统理论课程教学案例的设计[J]. 电气电子教学学报, 2013, 35(2): 21-23. [4]王立红. 任务驱动法在自动控制理论课程教学中的应用[J]. 辽宁工业大学学报: 社会科学版, 2014, 6(6): 127-128. [5]尤文斌, 丁永红. 自动控制理论实验教学研究[J]. 中国教育技术装备, 2011, 231(9): 109-110. [6]龚克. 关于卓越工程师培养的思考与探索[J]. 中国大学教学, 2010, 8: 4-5. [7]林健. 卓越工程师教育培养计划专业培养方案研究[J]. 清华大学教育研究, 2011, 32(2): 47-55. Teaching Case Design of Intelligent Control Course Based on Inverted Pendulum WEI Li-sheng, WU Xu, GUO Xing-zhong (School of Electrical Engineering, Anhui Polytechnic University, Wuhu Anhui 241000, China) In order to carry out the National Excellent Engineer Education and Training Program and improve the quality of the teaching of intelligent control course, the paper introduces case teaching into the whole teaching system. Through the inverted pendulum system of intelligent control strategy analysis and research practice, combined with intelligent control theory teaching requirements, the grey prediction golden controller is designed as a teaching case based on characteristic model and good results are achieved. This has not only completed the syllabus requirements of intelligent control, but also effectively improved the students' abilities to study and resolve the practical problems. intelligent control; case teaching; inverted pendulum; grey prediction 1673-2103(2016)02-0112-06 2016-03-28 安徽省省级质量工程资助项目(2015jyxm177);安徽工程大学校级本科教学质量提升计划重点资助项目(2015jyxm09) 魏利胜(1978-),男,安徽巢湖人,副教授,博士后,研究方向:智能控制.郭兴众(1963-),男,安徽芜湖人,教授,研究方向:智能控制. G642.0 A


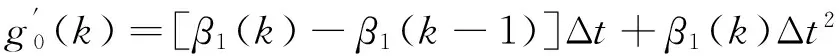
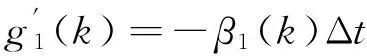

3 实验验证
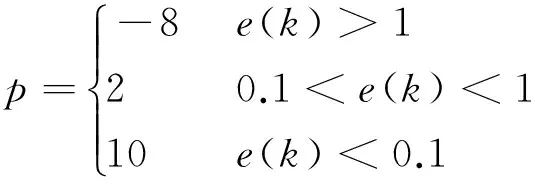



4 结束语

