鲜活农产品市场替代与整合研究——以水果为例

宋长鸣，周锦，赵晓飞

（1. 华中农业大学经济管理学院，湖北 武汉430070；2. 中南民族大学管理学院，湖北 武汉 430074）

鲜活农产品市场替代与整合研究
——以水果为例

宋长鸣1，周锦1，赵晓飞2

（1. 华中农业大学经济管理学院，湖北 武汉430070；2. 中南民族大学管理学院，湖北 武汉 430074）

在验证由苹果、香蕉和橙子所组成的水果市场相互影响的基础上，以向量自回归模型为基础，采用脉冲响应函数和方差分解的方法分析三类水果市场基于替代的动态影响关系；并运用多变量条件异方差模型论证三类水果市场的整合性，探讨大宗水果品种间的替代关系。结果表明，三类水果价格相互影响，正因为替代关系的存在，三类水果中任何一类水果市场受到正向外部冲击时其价格上涨的幅度有下降的趋势；苹果对香蕉和橙子的替代性较强，分担来自各类水果市场上涨压力的贡献较大，分别为82%、51%和71%；以苹果、香蕉和橙子为代表的水果市场整合程度高且稳定，外部冲击对水果市场内部替代关系的影响并不显著。水果市场虽然品种多，质量参差不齐，但政府可以通过调控替代性强的苹果的生产和供给来缓解整个水果市场价格波动的剧烈程度，水果市场支持政策的出台应考虑水果品种相互间的影响关系。

水果；替代；整合；VECH模型；VAR模型

宋长鸣， 周锦， 赵晓飞. 鲜活农产品市场替代与整合研究——以水果为例［J］. 农业现代化研究， 2016， 37（3）: 534-541.

Song C M， Zhou J， Zhao X F. Study of the substitution and integration of fruit markets by the VECH model［J］. Research of Agricultural Modernization， 2016， 37（3）: 534-541.

国外有关农产品产业经济的研究常考虑替代品的作用。有文献分析研究农产品的相对营养状况［1］、进口压力［2］、供给变动趋势［3］、国际国内价格传导［4］、食品安全事件［5］时，考虑了替代品的作用。研究农产品价格变化影响因素时，有必要将替代品纳入分析框架，考察其可能带来的影响。国内已有文献研究农产品产业经济时考虑了替代品的作用。主要集中在以下两方面：首先是替代品市场变化对农产品价格的作用。王钊和姜松［6］探究菜价波动时发现：邻域蔬菜价格显著影响本地蔬菜价格，其研究结论表明不同主产区间蔬菜替代明显。张立中等［7］在探索生猪价格波动调控政策时，也考虑了肉鸡市场的变化。研究猪肉价格变动时，有研究将牛肉价格作为替代品进行分析［8］；研究禽蛋时均有文献［9］考虑了替代品的作用。其次是分析价格领域外的其它农业经济问题时，部分文献也考虑了替代品的作用。如蔬菜［10］、猪肉［11］消费量变动机理研究；绿色农产品消费［12］；小麦、棉花、蔬菜、粮食作物种植面积变化［13-15］等。在考察农产品价格变动影响因素时，部分文献也考虑了替代品的作用，但一般仅把替代品作为外生变量。替代是相互的，譬如当苹果价格波动影响香蕉价格时，香蕉价格的变动又会反作用于苹果价格。因而，研究替代品相互之间的作用关系时，从内生的视角去分析可能更符合经济现实。

各类水果价格波动原因虽然迥异，由于存在一定程度的同质性，各类水果品种间存在或多或少的替代关系，正因为替代关系的存在，各类水果市场相互影响，相互间需求交叉价格弹性并不为零。因此，虽然水果市场品种多，但可以考虑通过调控某类大宗水果的价格来缓解整个市场价格波动的剧烈程度。本文欲以大宗水果品种苹果、香蕉、橙子为例，采用脉冲响应函数和方差分解的方法分析三类水果市场基于替代的动态影响关系；并运用多变量条件异方差模型论证三类水果市场的整合性，为政府调控水果市场提供政策建议。

1 研究方法

本文首先建立了向量自回归模型（VAR），并在此基础上进行脉冲响应函数和方差分解分析。介绍VAR模型的文献较多，脉冲响应函数和方差分解方法的应用也较为成熟，这部分将重点说明VECH类模型。构建VAR模型是为了进一步建立多变量自回归条件异方差模型（VECH）：VAR模型中的回归方程组为VECH模型的均值方程组，反应的是水果价格均值间的相互作用关系。而构建的VECH模型方差方程是为了反应水果价格条件方差之间的关系。

1.1 VECH模型

ARCH模型［16］和GARCH模型［17］的研究对象是单变量时间序列数据，为了研究多变量波动的相互影响，需要采用VECH模型。

式中：Ht为水果价格条件方差矩阵；C0为常系数矩阵；Ai和Bj分别为扰动项系数矩阵和条件协方差项系数矩阵；算子⊗为Hadamard乘积，表示的是前后矩阵内对应项相乘［18］，p和q分别表示扰动项和条件协方差项滞后的阶数。为减少方差方程待估参数的个数，Ai和Bj一般被限定为对称矩阵。由于一般GARCH（1，1）模型便可以模拟大量的时间序列数据，故确定p和q值为1。本文的研究对象有三个变量：苹果、香蕉和橙子价格，故确定变量个数为3。假设矩阵Ht对角线上的元素为hnnt，hnnt即为所构建的水果价格VAR模型第n个内生变量所对应VECH模型中方差方程的条件方差；假设矩阵Ht非对角线上的变量为hmnt，hmnt（m≠n）为第m 和n个内生变量的条件协方差；估计过程中，限定常系数矩阵为标量，即矩阵内各元素均相等。

1.2 格兰杰因果关系检验

苹果、香蕉和橙子互为替代品，理论上替代关系的存在会促使这三类水果价格相互影响。若苹果价格上涨，消费者对香蕉和橙子需求的改变导致这两类替代品价格发生变化；替代品价格的变化又会反作用于苹果价格。这意味着若从经验数据出发，模型结果应表明苹果、香蕉和橙子价格之间的相互影响。

采用格兰杰因果关系检验模型分析这三类水果价格之间的经验关系，为下一步建立VAR模型打下基础。建立VAR模型前，首先需要验证所分析的时间序列变量统计上互为格兰杰因果关系，不然VAR模型运用的前提条件就不成立。格兰杰解决了变量X是否引起变量Y的问题，即分析当前的变量Y能够多大程度被过去的变量X解释，加入X的滞后值能否使解释程度提高，如果变量Y受到变量X的滞后影响，说明两个变量之间具有格兰杰因果关系［19］。

1.3 脉冲响应函数分析

由于所建的VAR模型是一个动态的内生系统，外部冲击对系统内各内生变量的影响是动态而又相互交织的。脉冲响应函数反映系统中一个内生变量的外部冲击对系统内所有内生变量影响的轨迹，若在第0期给苹果价格一个外部冲击，则通过所构建的VAR内生系统，会得到苹果、香蕉、橙子价格一系列的值，这些所求得的结果为由苹果价格的脉冲所引起的苹果、香蕉和橙子价格的响应函数［19］，同理，对于香蕉和橙子价格的外部冲击也可以得到一系列的值。脉冲响应函数反映了来源于系统一个内生变量的外部冲击对系统内其它变量各期影响的轨迹。

1.4 数据来源

本文的研究期限为2002年1月至2014年5月，共计149个时间序列样本。由于连续性可比时间序列价格数据获取的困难，本文选取水果市场中典型的大宗品种苹果、香蕉和橙子作为研究对象。其中苹果、香蕉和橙子价格数据来源于2003-2013年的《中国农产品价格调查年鉴》，2013年1月至2014 年5月的数据来源于各期的《中国统计月报》。本文中苹果、香蕉和橙子的零售价格（元/kg）指的是水果主产区集贸市场的成交价格，具体说明详见《中国农产品价格调查年鉴》中的附录。

2 实证结果与分析

2.1 水果价格平稳性检验分析

以不平稳的时间序列变量建模，得出的结论可能会出现偏差。在采用苹果、香蕉和橙子价格建模时，有必要对价格序列进行平稳性检测。表1显示了三类水果价格平稳性检验结果。苹果价格ADF平稳性检验结果对应P值为0.0253，在97.47%的置信度下拒绝序列不平稳的原假设。同理，香蕉、橙子价格平稳性检验所对应t统计量均表明其在0.01的显著性水平下拒绝序列不平稳的原假设。总之，样本期内苹果、香蕉和橙子价格序列平稳。

表1 苹果、香蕉、橙子价格平稳性检验结果Table 1 Stationary test results of main fruit prices

2.2 水果价格相互间的格兰杰因果关系分析

格兰杰因果关系模型结果对滞后期的选择较为敏感，本部分共列示了滞后1-10期所对应的F统计量（表2）。表中共60个F统计量，其中有51个统计量表明至少能够在10%的显著性水平下拒绝原假设，比例高达85%。即大部分F统计量表明可以接受“苹果、香蕉和橙子价格互为格兰杰因果关系”的结论。总之，格兰杰因果关系检验模型从经验上验证了苹果、香蕉和橙子价格相互影响的结论。

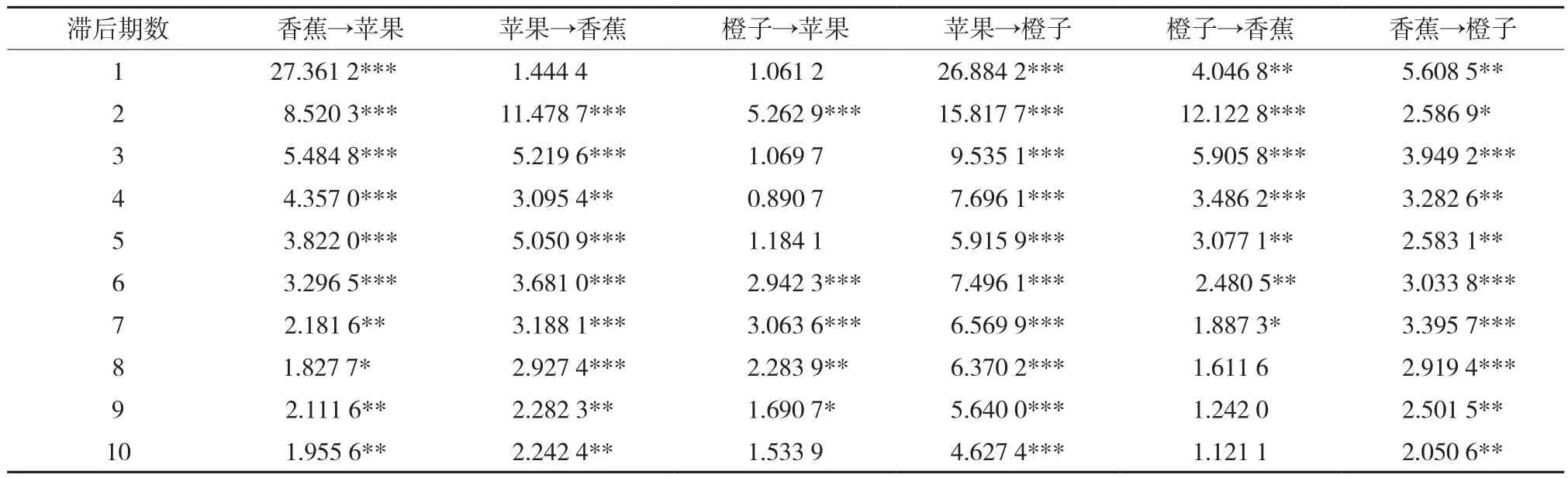
表2 苹果、香蕉、橙子价格格兰杰因果关系模型检验结果Table 2 Grange causality model results of main fruit prices

2.3 水果价格动态影响程度分析

格兰杰因果关系检验模型从经验上验证了苹果、香蕉和橙子价格经验上相互影响的结论，但没有回答作用程度的问题。三类水果价格相互影响，为进一步采用VAR模型打下基础。在构建VAR模型前，首先要确定模型的滞后阶数。滞后1-10阶时各统计量所表明的最优滞后阶数选择结果（表3）表明，LR、FPE、AIC这三个统计量所决定的VAR模型最优滞后阶数为7阶，而SC和HQ这两个统计量所决定的最优滞后阶数为2阶。考虑到FPE和AIC这两个统计量滞后2阶和7阶统计量值相差较小，且为了减少下文所建VECH模型的待估参数，本文确定VAR模型的滞后阶数为2阶。

表3 向量自回归模型滞后阶数的选择Table 3 Lag order choice of VAR model

由于VAR模型具有动态的特征，估计的回归系数经济意义并不明显，建立VAR模型的目的是为采用脉冲响应函数和方差分解分析打下基础。脉冲响应函数能清晰反应VAR系统内某一经济变量受到冲击时，其它变量动态响应的过程。对于水果市场而言，若苹果价格受到冲击而发生波动，由于替代关系的存在，香蕉和橙子价格也会相应发生变动，同时也会反作用于苹果价格。因苹果价格受到冲击所导致的三类水果价格的动态变化情况构成了各自的脉冲响应函数。

当苹果价格受到一单位标准差新息的冲击时，苹果和香蕉价格上涨明显，橙子价格出现明显振动（图1）。第1期苹果价格上涨约0.19元/kg；第2期和第3期上涨幅度逐步增加，达0.33元/kg和0.37元/kg；从第4期开始逐步下降，直至第6期后上涨幅度逐步稳定在0.31元/kg左右。来自苹果市场正向的外部冲击也促使香蕉价格出现了明显上涨，上涨幅度由第2期0.03元/kg逐步上涨至第5期的0.21元/kg；从第6期起上涨幅度逐步回落到第9期的0.13元/kg，之后各期逐步保持稳定。受苹果市场的冲击，橙子价格振动明显，但上涨幅度比较小，第2-6期橙子价格稍微下降，第7期开始出现明显的上涨趋势。总之，来自苹果市场的冲击不仅会影响苹果价格，还会促使香蕉和橙子价格发生显著变化。

图1 各类水果价格对苹果价格一个标准差新息的响应Fig. 1 Response of apple price to Cholesky One S.D. innovation

当香蕉市场受到一个标准差单位新息的冲击时，香蕉和苹果价格会显著上涨，橙子价格经历短暂下降后也恢复上涨的态势（图2）。香蕉价格上涨明显，但各期上涨幅度波动较大。第1期和第2期香蕉价格分别上涨0.21元/kg和0.28元/kg，从第3期开始上涨幅度逐渐下降至第9期的0.01元/kg，之后几期上涨幅度又缓慢抬头。来自香蕉市场的冲击致使苹果价格上涨幅度较大，由第1期0.09元/kg上涨至第4期的0.18元/kg，之后逐渐下降，最后稳定在0.14元/kg左右。第2-4期橙子价格先经历小幅下跌，之后各期出现明显上涨。来自香蕉市场的冲击不仅影响香蕉价格，并对苹果和橙子价格也产生了显著影响。

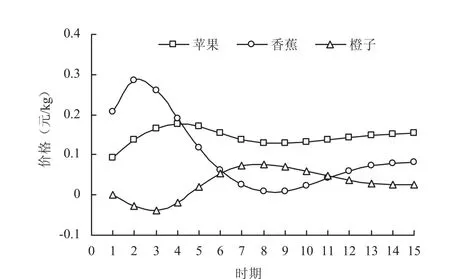
图2 各类水果价格对香蕉价格一个标准差新息的响应Fig. 2 Response of banana price to CholeskyOne S.D. innovation

来自橙子市场的冲击也显著影响了苹果和香蕉的价格（图3）。橙子价格第1期和第2期上涨幅度分别为0.17元/kg和0.18元/kg，从第3期开始，上涨幅度逐渐下降到第7期的0.06元/kg，第8期起，稳定在0.05元/kg左右。来自橙子市场的冲击促使苹果价格显著上涨，且上涨幅度逐期增加。第1期上涨幅度为0.05元/kg，并逐渐上升到第11期的0.22 元/kg，之后各期稳定在0.22元/kg左右。橙子市场价格的变动促使香蕉价格上涨，上涨幅度波动明显。第1期到第5期上涨幅度稳定在0.05元/kg左右，此后逐渐上涨，上涨至第8期的0.11元/kg，之后各期稳定在0.09元/kg左右。来自橙子市场的正向冲击也促使苹果和香蕉价格显著上涨。

图3 各类水果价格对橙子价格一个标准差新息的响Fig. 3 Response of orange price to Cholesky One S.D. innovation

总之，来自苹果、香蕉和橙子市场任何一类水果的外部冲击除了导致自身价格发生明显波动外，还会影响其它两类水果的价格。该过程就是其它水果市场对所受冲击水果替代的过程。图1、图2和图3清楚地展示了当某类水果价格受到正向冲击时，该类水果价格首先会明显上涨，但随着时间推移，上涨幅度均会经历下降的过程，这在香蕉和橙子市场体现得更为明显。正因为替代水果品种的存在，才导致上涨幅度发生明显下滑，从而降低所受冲击水果市场价格波动的剧烈程度。

脉冲响应函数表明苹果价格波动对整个水果市场影响较大。当苹果市场受到冲击时，其价格上涨幅度虽然从第4期开始出现下降，但下降幅度并不大（图1）；但当香蕉和橙子市场受到冲击时，开始几期其上涨幅度较大，但之后苹果价格上涨幅度分别于第5期和第3期超过香蕉和橙子价格的上涨幅度（图2和图3），这表明苹果市场对香蕉和橙子价格变化较为敏感，即苹果对香蕉和橙子的替代作用明显。这启示着可以基于水果品种间的替代关系，通过调控苹果生产和供给，间接降低整个水果市场价格波动的剧烈程度。

2.4 水果市场替代程度分析

水果市场内苹果、香蕉和橙子替代关系的存在会导致这三类水果价格相互影响，脉冲响应函数刻画了当某类水果价格变化时，各水果品种价格随时间动态变化的情况。不同水果品种之间存在一定程度的异质性，虽然互为替代品，但不可能完全替代。方差分解的目的是探究当某类水果价格受到外部冲击时，其它水果品种通过替代分担外部冲击的大小。替代品的存在可以减缓外部冲击后水果价格波动的剧烈程度。

图4 苹果市场受冲击方差分解结果Fig. 4 Variance of decomposition of apple

当苹果市场受到正向冲击面临上涨压力时，其主要通过自身价格的变化来分担上涨压力，香蕉市场也会分担一部分来自苹果市场的上涨压力，橙子市场贡献较小（图4）。具体而言，第2期苹果市场几乎分担了外部冲击所造成的全部上涨压力，贡献比例达到99%，但余下几期的贡献逐步下降，直到降低到第8期的81.65%。与此同时，香蕉市场分担

力的贡献比例逐渐增加，从第2期的0.63%上涨至第7期的18.07%。苹果市场贡献逐步下降而香蕉市场贡献逐步上升的过程也就是由于苹果价格上涨，香蕉对苹果的替代过程，正因为香蕉市场的替代，苹果市场由于外部冲击所导致的波动程度才有所缓和。从第9期开始，苹果和香蕉市场所承担上涨压力的贡献逐步稳定，分别在82%和16%上下浮动。橙子市场分担苹果市场上涨压力的贡献比例较低，虽然呈现出缓慢上涨的趋势，但最高时不超过2%。

同理，当香蕉市场受到正向外部冲击面临上涨压力时，其通过自身价格的上涨分担了一部分压力，苹果市场在缓解香蕉价格上涨的过程中发挥了重要作用，橙子市场也有一定的贡献（图5）。第1期香蕉市场分担上涨压力的贡献为83.11%，之后下跌明显，直至降低至第15期的43.63%，但下降幅度逐步减小。与此同时，苹果市场的贡献逐步增加，由第1期的16.89%上涨至第15期的51.34%。值得注意的是，从第13期开始，苹果市场分担上涨压力的贡献超过了香蕉市场，表明苹果市场对来自于香蕉市场的外部冲击较为敏感，苹果对香蕉的替代性较强。橙子市场也有一定的贡献，且贡献比例逐步上升，从第9期开始，稳定在5%左右。

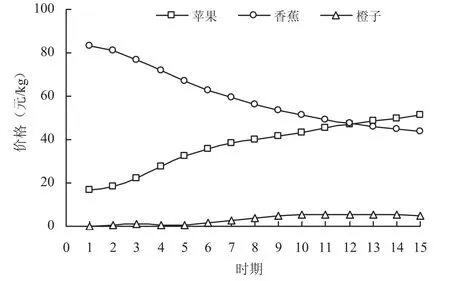
图5 香蕉市场受冲击方差分解结果Fig. 5 Variance of decomposition of banana

当橙子市场受到正向外部冲击面临上涨压力时，苹果和香蕉市场在分担其上涨压力的过程中发挥了重要作用（图6）。第1期橙子市场承担的上涨压力贡献为85.32%，随着时间的推移，其贡献比例逐步下降，直至下降到第15期的15.55%。与此同时，苹果市场承担来自橙子市场上涨压力的贡献比例逐渐增加，由第1期的9.19%上涨至第15期的70.77%。值得注意的是，从第5期开始，苹果市场的贡献就已超过橙子市场本身。这意味着苹果价格对橙子价格的变动较为敏感，前者对后者的需求交叉价格弹性较大。香蕉市场所承担上涨压力的贡献也在波动中显现出明显的上涨趋势，第1期大小为5.50%，从第10期开始，贡献比例稳定在13%左右。总之，苹果、香蕉和橙子价格相互影响，相互间的替代程度存在一定差异。苹果市场对来自任何一类水果市场价格变动的信息均较为敏感，价格变化较大，分担各类水果市场上涨压力的贡献也较大。其中，苹果市场中，苹果价格分担上涨压力的贡献一直最高；其在香蕉和橙子市场分担上涨压力的贡献也持续上涨，分别于第13期和第5期超过它们自身的贡献比例。这意味着苹果对香蕉和橙子的替代作用较强。这进一步佐证可以通过稳定苹果的供给和价格来缓解整个水果市场价格波动的剧烈程度。

图6 橙子市场受冲击方差分解结果Fig. 6 Variance of decomposition of orange

2.5 水果市场整合性分析

消费者购买偏好和苹果、香蕉及橙子在一定程度上满足消费者需求的同质性是这三类水果相互替代的基础。格兰杰因果关系检验模型也从经验上表明苹果、香蕉和橙子价格相互影响。这部分分析的重点在于考量三类水果价格两两间相互作用的关系是否会受外部冲击的影响，也就是说，水果市场内部的整合性是否稳定？

本部分在VAR模型的基础上，采用VECH模型，针对所研究水果价格序列的条件方差或条件协方差建模，估计过程中，为了减少VECH模型中待估参数个数，本文将残差项系数矩阵和条件方差项系数矩阵的秩均设定为1。表4显示了VECH模型方差方程组运行的结果。苹果、香蕉和橙子这三类水果价格方差方程所对应的扰动项系数a11、a22和a33均不显著，而条件方差项系数b11、b22和b33均在0.01的显著性水平下拒绝原假设，这表明苹果、香蕉和橙子价格的条件方差主要受前期条件方差的影响，而外部冲击的影响并不显著。方差常用来衡量波动的大小，这表明这三类水果价格本期的波动主要是其前期自身波动信息传导的结果。同理条件协方差方程中残差项系数amn（m≠n）所对应的Z统计量表明不能拒绝回归系数为零的原假设，而条件协方差项系数bmn（m≠n）所对应的P值均远小于0.01。这表明三类水果价格所对应的本期条件协方差项也主要是由前期条件协方差项所影响，而前期外部冲击影响的结果并不显著。条件协方差反映的是所研究经济变量的联合波动情况，这意味着水果价格间的相互作用关系是内生的，外部冲击影响并不显著，这种联合的波动关系基于水果间的替代。正由于水果市场中相互间基于替代内生关系的存在，才将各水果品种整合成一个大的水果市场，且水果市场内部的整合性较为稳定，任何一类水果价格受到外部冲击时，其它水果品种价格也会受到影响。

表4 水果市场VECH模型估计结果Table 4 Results of VECH model of fruit markets

3 结论

苹果、香蕉和橙子价格相互影响，来自任何一类水果的外部冲击除了导致自身价格发生明显波动外，还会影响其它两类水果的价格。经验数据表明，当格兰杰因果关系检验模型滞后1-10阶时，多数F统计量证实三类水果价格互为格兰杰因果，即这三类水果价格相互影响。脉冲响应函数反映当某类水果价格受到冲击时，各类水果价格随时间变化的过程，也即为相互替代影响的过程。正因为替代关系的存在，才缓解了所受冲击水果市场价格上涨的幅度。方差分解结果表明苹果市场在承担各类水果市场因外部冲击而导致的上涨压力中扮演重要作用，苹果价格对香蕉、橙子及其自身市场的外部冲击变化较为敏感，即苹果对香蕉和橙子的替代性强，这意味着可以重点调控苹果的生产和供给来缓解整个水果市场价格的波动程度。显然，各类水果市场间相互影响的关系意味着调控某一类水果市场时，要充分考虑对其它类别水果市场带来的影响，主要水果市场的波动会传导至其它水果市场，政府相关调控措施的出台要从水果市场全局出发，考虑各类水果市场之间内在的替代影响关系。同时，某类水果市场受到诸如气候灾害、虫灾、食品安全等突发性事件的冲击时，除了评估该类水果市场所受到的影响，还应考虑对其它类别水果市场可能带来的冲击。

苹果、香蕉和橙子所构成的水果市场整合程度较高。外部冲击对三类水果两两间相互的替代关系影响并不显著。水果市场稳定的整合性质为调控水果市场价格波动程度提供了思路：水果市场品种多，调控难度大，但可以通过稳定苹果供给来降低整个水果市场价格波动的剧烈程度。这实质上是从一定程度上牺牲了水果市场的多样性来保证水果市场价格的稳定性，即通过稳定苹果这一类水果价格，来缓解整个水果市场价格波动的幅度。多样性的水果市场能增加消费者的福利，消费者消费习惯在一定时间内变动小，这客观上要求政府在保持品种多样性和减缓水果价格波动幅度间取得平衡。

［1］ Akaichi F， Gil J M， Nayga R M. Assessing the market potential for a local food product evidence from a non-hypothetical economic experiment［J］. British Food Journal， 2012， 114（1）: 19-39.

［2］ Garcia A C， Martinez G， Villanueva M. A trade model to evaluate the impact of trade liberalization on EU tomato imports［J］. Spanish Journal of Agricultural Research， 2009， 7（2）: 235-247.

［3］ Hendricks N P， Sumner D A. The effects of policy expectations on crop supply， with an application to base updating［J］. American Journal of Agricultural Economics， 2014， 96（3）: 903-923.

［4］ Abbott P， de Battisti A B. Recent global food price shocks: Causes，consequences and lessons for African governments and donors［J］. Journal of African Economies， 2011， 20（1）: 112-162.

［5］ Arnade C， Calvin L， Kuchler F. Consumer response to a food safety shock: The 2006 food-borne illness outbreak of E-coli O157: H7 linked to spinach［J］. Review of Agricultural Economics，2009， 31（4）: 734-750.

［6］ 王钊， 姜松. 我国蔬菜价格变动的空间计量分析［J］. 农业技术经济， 2013（11）: 4-14. Wang Z， Jiang S. The spatial econometrics analysis of vegetable price in China［J］. Journal of Agrotechnical Economics， 2013（11）: 4-14.

［7］ 张立中， 刘倩倩， 辛国昌. 我国生猪价格波动与调控对策研究［J］.经济问题探索， 2013（11）: 117-122. Zhang L Z， Liu Q Q， Xin G C. Study of live pig price fuctuation and policies［J］. Inquiry into Economic Issues， 2013（11）: 117-122.

［8］ 段隐华， 王刚. 四川猪肉价格波动的影响因素分析——基于VAR模型［J］. 四川农业大学学报， 2011， 29（4）: 580-584. Duan Y H， Wang G. Analysis of infuential factors for pork price fluctuating in Sichuan: Based on VAR model［J］. Journal ofSichuan Agricultural University， 2011， 29（4）: 580-584.

［9］ 蔡少杰， 周应恒. 内生结构性， 短期外生冲击与鸡蛋价格波动［J］.湖南农业大学学报（社会科学版）， 2014， 15（3）: 21-26. Cai S J， Zhou Y H. Endogenous and short-term external impact on egg price fuctuation in China based on panel date of 31 provinces （cities or prefectures） from 2005 to 2011［J］. Journal of Hunan Agricultural University （Social Sciences）， 2014， 15（3）: 21-26.

［10］ 王方舟. 河北省农村居民蔬菜消费量的因素分析［J］. 广东农业科学， 2012（5）: 225-228. Wang F Z. Factor analysis of vegetable consumption of rural residents in Hebei Province［J］. Guangdong Agriculture Sciences，2012（5）: 225-228.

［11］ 虞祎， 胡浩， 刘莹. 我国城乡两市场的猪肉价格的影响因素分析［J］. 南京农业大学学报（社会科学版）， 2009， 9（2）: 38-42. Yu Y， Hu H， Liu Y. Analysis on infuencing factors for pork price in urban and rural markets based on the equilibrium transfer model［J］. Journal of Nanjing Agricultural University （Social Sciences Edition）， 2009， 9（2）: 38-42.

［12］ 靳明， 赵昶. 绿色农产品消费意愿的经济学分析［J］. 财经论丛，2007（6）: 85-91. Jin M， Zhao C. Economic analysis of consuming willingness to green agricultural products［J］. Collected Essays on Finance and Economics， 2007（6）: 85-91.

［13］ 刘俊杰， 周应恒. 我国小麦供给反应研究——基于小麦主产省的实证［J］. 农业技术经济， 2011（12）: 40-45. Liu J J， Zhou Y H. The supply response research of wheat market in China: Based on the main producing area［J］. Journal of Agrotechnical Economics， 2011（12）: 40-45.

［14］ 钟甫宁， 胡雪梅. 中国棉农棉花播种面积决策的经济学分析［J］.中国农村经济， 2008（6）: 39-45. Zhong F N， Hu X M. The economic analysis of cotton farmers' planting decision-making in China［J］. Chinese Rural Economy，2008（6）: 39-45.

［15］ 吕超， 周应恒. 我国蔬菜播种面积的影响因素分析［J］. 经济地理， 2011， 31（1）: 118-122. Lü C， Zhou Y H. The analysis of infuencing factors of vegetables' sown area in China［J］. Economic Geography， 2011， 31（1）: 118-122.

［16］ Engle R F. Autoregressive conditional heteroscedasticity with estimates of the variance of U.K. inflation［J］. Econometrica，1982（4）: 987-1008.

［17］ Bollerslev T. Generalized autoregressive conditional heteroscedasticity［J］. Journal of Econometrics， 1986， 31（3）: 307-328.

［18］ 易丹辉. 数据分析与EViews应用［M］. 北京: 中国人民大学出版社， 2008. Yi D H. Data Analysis and the Application of EViews［M］. Beijing: China Renmin University Press， 2008.

［19］ 高铁梅. 计量经济分析方法与建模：Eview应用及实例［M］. 北京: 清华大学出版社， 2009. Gao T M. Econometric Methods and Models: The Applications and Examples of Eviews［M］. Beijing: Tsinghua University Press，2009.

（责任编辑：童成立）

Study of the substitution and integration of fruit markets by the VECH model

SONG Chang-ming1， ZHOU Jin1， ZHAO Xiao-fei2
1. College of Economics and Management， Huazhong Agricultural University， Wuhan， Hubei 430070， China；2. School of Management， South-Central University for Nationalities， Wuhan， Hubei 430074， China）

Applying the Impulse Response Function and Variance Decomposition method， this paper analyzed the interaction effect and the dynamic substitution relationship among the apple， banana， and orange markets. In addition，this paper also applied the VECH model to examine the substitution and integration effects of the main fruit markets. Results show that the prices of apple， banana and orange affected each other because of substitution effects. When fruit markets were struck by external shocks， the price increasing trend tended to decrease. Apple showed strong substitution effect for banana and orange. Apple market contributed a lot on alleviating other fruit markets' upward pressure caused by external factors， that is， 82%， 51% and 71%， respectively. In addition， the three-fruit markets were integrated tightly and steadily and external shock did not affect the substitutions among fruit markets signifcantly. The above conclusions imply that even there are many kinds of fruits and it is hard to regulate fruit markets. The Government could regulate the apple supply and price to alleviate the whole fruit market fuctuations because apple as strong substitution effect for other fruits.

fruits； substitution； integration； VECH model； VAR model

新世纪以来，我国水果产业蓬勃发展，供给能力不断加强，果农收入增长明显；且花色品种越来越丰富，满足了消费者多样化的需求；快速发展的水果产业进一步夯实了农村发展和农民生活的物质基础，为区域农业经济增长作出了重要贡献。水果产量自1995年以来增产趋势明显，除2000年略有下跌外，一直保持较快的增长态势，最低增长率也达到4.42%；2003年水果产量增长率甚至高达10.88%。2012年水果总产量为24 057万t，约为1995年的5.71倍，在不考虑流通损耗的前提下，相当于每个中国人日均消费0.49 kg。水果总产量的稳定增长是水果价格稳定的基础，但新世纪以来水果价格波动频繁剧烈。以2002年为基期计算出来的居民消费价格分类指数（鲜果类）波动剧烈，且呈现出明显的上涨趋势。2003年1月至2012年12月期间，鲜果类价格有48个月份波动幅度不低于10%，占样本总数的40%，2006年6月价格上涨更是高达49.2%。水果价格的波动影响了果农、消费者和各级中间商的利益；水果市场品种繁多，在给消费者带来多样化选择的同时，也增加了调控的难度，研究水果市场的替代与整合具有显著的政策和现实意义。

National Natural Science Foundation of China （71503093）； the Major Program of the National Social Science Foundation of China （12&ZD048）； the Fundamental Research Funds for the Central Universities （2662014BQ044）.

SONG Chang-ming， E-mail: scm@mail.hzau.edu.cn.

26 August， 2015；Accepted 13 December， 2015

F323.7

A

1000-0275（2016）03-0534-08

10.13872/j.1000-0275.2016.0004

国家自然科学基金项目（71503093）；国家社会科学基金重大项目（12&ZD048）；中央高校基本科研业务费专项基金资助（2662014BQ044）。

宋长鸣（1986-），男，湖北公安人，博士，讲师，主要从事农产品价格方面的研究，E-mail: scm@mail.hzau.edu.cn。

2015-08-26，接受日期：2015-12-13