基于动态规划的单线阵影像自动分段技术

杨成敏，胡 坚，黎荆梅

（1.中国科学院定量遥感信息技术重点实验室 北京 100094；2.中国科学院光电研究院 北京 100094；3.中国科学院大学 北京　100049）

基于动态规划的单线阵影像自动分段技术

杨成敏1，2，3，胡 坚1，2，黎荆梅1，2

（1.中国科学院定量遥感信息技术重点实验室 北京 100094；2.中国科学院光电研究院 北京 100094；3.中国科学院大学 北京100049）

针对搭载有GPS/IMU的航空单线阵影像几何纠正中的影像分段问题，提出了一种使用了动态规划的思想，利用二次多项式对影像各行POS数据的角元素进行拟合，通过多阶段搜索迭代使得拟合误差最小，最终得到最佳分段的方法。实验表明，该算法可以根据POS数据中的角元素变化趋势对影像进行自动分段，能有效降低拟合误差，提高纠正精度。

单线阵影像；动态规划；自动分段；POS数据

在使用基于点和直线特征的几何纠正方法对航空单线阵影像进行纠正时，影像分段是建立平差的基础，错误的分段可能导致外方位元素求解精度不高，甚至无法收敛。对于使用点和直线特征进行航空单线阵影像几何纠正方法来说，制约其纠正效果的一个重要原因是影像的分段［1-3］。国外学者Changno Lee使用了均匀分段在中低分辨率的航空单线阵影像中取得了较好的效果［4］。但是这种方法并不适合于高分辨率影像的几何纠正，并且不能很好的根据预知的POS数据较好的判断分段大小［5-6］，国内目前还没有针对几何纠正的相关分段方法的研究。因此，研究高分辨率航空单线阵影像几何纠正中的分段技术显得尤为重要。

文中针对预知影像的POS数据，提出了一种基于动态规划，使用二次多项式对POS数据的角元素进行拟合，以分段内拟合误差平方和为代价函数，以影像所有点拟合误差为目标函数，通过多阶段搜索以最小化目标函数，最终迭代多次得到最佳分段的方法。该算法能有效的利用POS数据中角元素的变化趋势对影像进行自动分段。

1　基于动态规划的影像自动分段原理

动态规划是运筹学的一个分支，是求解多段决策过程最优化的数学方法，其基本思想是将多阶段过程转化为一系列的单阶段问题，利用各阶段之间的关系，逐个求解，从而得到问题的最优解。

传统的影像分段方法为均匀分段，即每个分段大小一致［4］。这种方法的优点是简单，不需要额外的算法，缺点是不能很好的利用给定的POS数据进一步提升几何纠正精度。本文在研究了已有的基于曲线进行分段的方法基础上，提出了一种根据POS数据基于动态规划的单线阵影像自动分段方法。

图1　单线阵影像分段示意图Fig.1　Sketch map of segmentation of single linear array image

首先假设一个单线阵影像分为N个影像段，如图1所示，然后对POS数据的角元素进行拟合，则每个影像段内拟合的误差平方和为ei（1≤i≤N），i表示分段号，则影像内所有分段的误差平方和为式（2）。

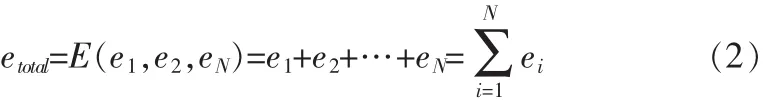
为使平差效果最理想，需使etotal最小化，即

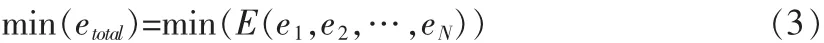
通过采用动态规划的思想可以求解这个问题。每个分段的误差平方和ei为代价函数，为目标函数。对于第i个分段来说，其分段的大小是由左右两个边界决定，即由第i-1和第i+1个分段共同决定。所以，第i个分段的误差为式i=E（ei-1，ei，ei+1）。且第i分段的误差仅与第i-1和第i+ 1个分段有关。于是，式（2）可等价于

则式（3）等价于

因此，求解目标函数最小化的可以分为多个阶段，且每个求解阶段与上一阶段有联系。应用动态规划的思想求解可以得到，对于第i个阶段Si，有式（6）

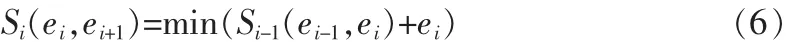
其中，S（i-1，ei）为上一个阶段的最优解，表示第i-1个分段的左边界和第i-1个分段的右边界（即第i个分段的左边界）已经确定，且此时第i+1个分段的右边界固定。

图2　一个分段示例Fig.2　A example of segmentation

我们来考虑一个简单的例子。假设共分为5段，即N=5，每个边界有3个选择：左边，中间，右边，如图2所示。那我们需要计算各个阶段的最优解，如式（7）所示

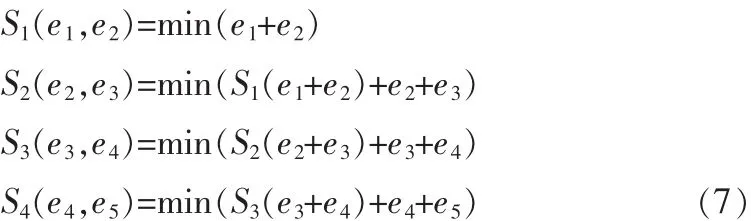
通过阶段S1可以确定第1个分段的右边界，通过阶段S2可以确定第2个分段的右边界，以此类推，通过阶段Si可以确定第i个分段的右边界，最后一个边界为影像末尾行。

2　算法求解

2.1代价函数计算

对于单线阵影像来说，每个分段的误差平方和ei是通过平差时得到的。根据先期实验，在能够平差的条件下，每个分段大小在5～50之间。考虑在极限条件下，相邻两个分段大小均为5，则根据式，每个分段的未知数个数为15个，假设有a个控制点，b个直线特征点，则共有未知数15*2+b，能建立误差方程共2a+2b个，需满足15*2+b<2a+2b，即2a+b＞30。对于大小为5的两个相邻分段来说，控制点总个数a一般不超过4个，当只有一个直线特征，则b不超过10，则不满足2a+b＞30。因此在平差中计算代价函数ei是不可以的。考虑到最终的目标为对POS数据的修正，即通过使用多项式对POS数据分别进行拟合，求得最优解，因而在根据预知的POS数据对单线阵影像分段时采用了多项式拟合，并使用拟合后与原数据的误差作为代价函数ei，从而可以得到单线阵影像分段的边界。

2.2最大分段数目的确定

通过坐标转换，可将GPS/IMU数据转换为摄影中心的外方位元素。虑到角元素与线元素的数量级不同，因此基于线元素和基于角元素分开拟合［4］，在经过大量实验分析，同线元素相比，角元素对于影像纠正的效果影像更明显。因此，本文中选取角元素作为最终的拟合分段的依据。

根据提取到同名特征点和同名特征直线后，根据平差条件：平差方程个数需大于未知数个数，可以求得最大分段数。

2.3算法流程

将上文中的算法总结归纳可得如下流程：

1）根据提取得到的同名点及同名直线个数计算最大分段数segCountMax，并根据搜索窗口大小设置分段间隔segGap，初始化分段数segCount；

2）根据分段数segCount和影像长度imgLength，平均化分段长度gap（i）=imgLength/segCount，以初始化每一个分段的边界；

3）设置迭代次数iterNum；

4）针对第i个分段内的右边界，在搜索区间内对角元素分别进行二次多项式拟合，计算每一个分段上所有点的拟合误差平方和，选取最小误差平方和所在位置为新的右边界，以此确定每一个分段间隔gap（i）；

5）迭代iterNum次，以使得影像内误差平方和不再变化，达到最小；

6）输出分段位置。

3　实验与结果

为了进一步分析分段的影像，选取了2011年7月贵州安顺机场的无人机飞行测试数据。实验中截取了一段830*1 030的线阵CCD原始影像，分辨率为0.5 m，如图3所示，用于参考的相应区域的正射影像分辨率为0.4 m。分别使用了均匀分段法和基于动态规划的自动分段法进行纠正，其中基于动态规划分段法相关参数设置如表1。使用文中所述的基于动态规划的影像自动分段方法对其进行自动分段。分段数为24至30，且每个分段数下迭代12次，分段数的搜索窗口为7，分段边界的搜索窗口为5。在每个分段数下的迭代中，如图4所示，随着迭代次数增多，分段内影像点的角元素拟合误差平方和在逐渐减小，最终达到一个最小值并不再变化，那么此时的分段即为当前分段数N下的最佳分段。将N为24至30的分段数汇总得到图5。如图5所示，在搜索窗口内当分段数为25时角元素拟合误差平方和最小，那么即选取25为最佳分段数。当N=25时迭代稳定时的分段即为最佳分段，如图6所示。分别使用两种分段方法对影像进行几何纠正，得到纠正影像局部对比图如图7所示。在两幅影像上分别选取了10对检查点，提取坐标并计算几何精度得到表2。同基于均匀分段的几何纠正方法相比，使用基于动态规划的影像自动分段方法纠正后，检查点误差在x方向上从0.91 m（1.82个像素）减少至0.68 m（1.36个像素），在y方向上从0.92 m（1.84个像素）减少至0.71 m（1.42个像素）。可以看出，文中提出的方法对单线阵影像内部几何畸变校正有很大的改善。

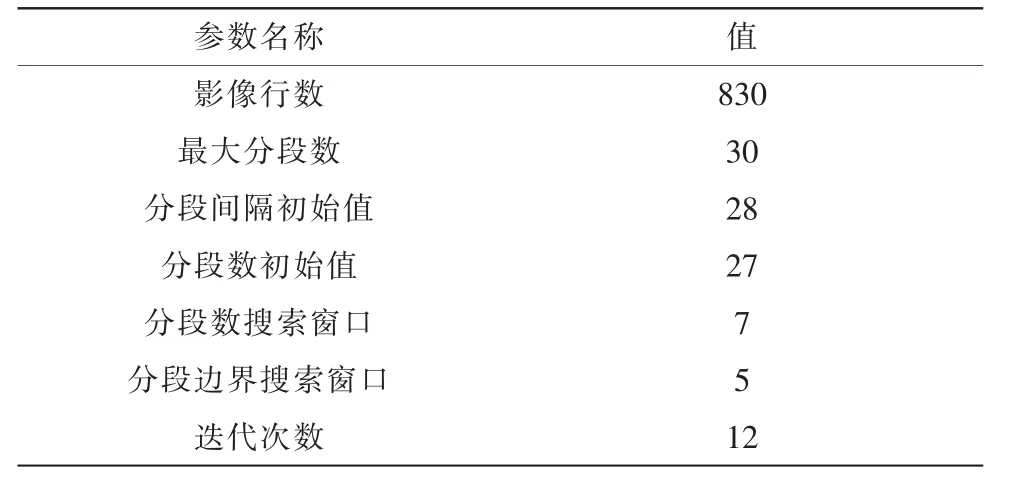
表1　参数设置Tab.1　Parameter setting

图3　原始影像Fig.3　The original single array image

图4　N=26时分段内误差平方和与迭代次数的关系Fig.4　Relation between error sum squares and iterations in a segment which N=26

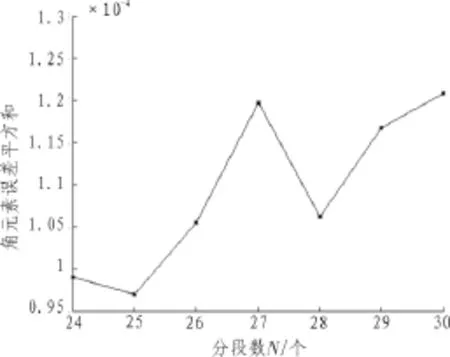
图5　影像误差平方和与分段数的关系Fig.5　Relation between error sum squares and numbers of segments

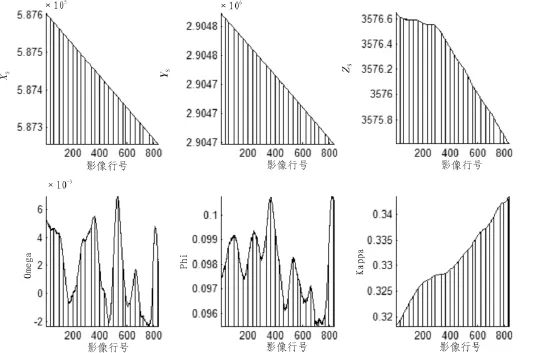
图6　分段结果Fig.6　The result of segmentation

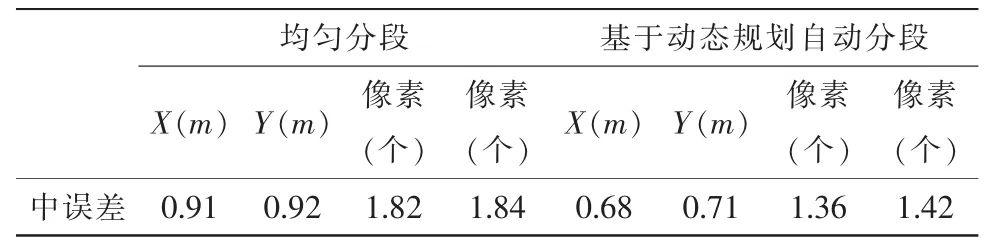
表2　几何纠正精度分析Tab.2　Analysis of geometric rectification accuracy

图7　几何纠正结果Fig.7　Result of geometric rectification

4　结束语

为了进一步提高影像的纠正精度，本文使用了基于POS数据的影像分段技术。针对POS数据的特点，提出了一种能有效改进纠正结果的影像分段方法。影像分段是外方位元素模型建立以及平差的基础，错误的分段可能导致外方位元素求解精度不高，甚至无法收敛。影像的自动分段需要基于POS数据，尤其是3个姿态角的数据变化趋势进行分析，同时结合段间平滑问题，确定合理的分段条件，以保证平差处理的有效性。文中提出了一种使用了动态规划的思想，利用二次多项式对影像各行POS数据的角元素进行拟合，以分段内拟合误差平方和为代价函数，以影像所有点拟合误差为目标函数，通过多阶段搜索以最小化目标函数，最终迭代得到最佳分段。实验表明，该算法能有效的根据POS数据中的角元素变化趋势对影像进行自动分段，在提高自动化作业的同时，能有效降低分段误差，提高纠正精度。

［1］李传荣.无人机遥感载荷综合验证系统技术 ［M］.北京：科学出版社，2014.

［2］Aldrich W S，Kappus M E，Resmini R G，et al.Hydice postflight data processing［C］//Aerospace/Defense Sensing and Controls.International Society for Optics and Photonics，1996：354-363.

［3］张浩，张兵，卫征.基于POS的高光谱影像快速几何纠正［J］.测绘通报，2009（1）：14-17.

［4］Lee C，Theiss H J，Bethel J S，et al.Rigorous mathematical modeling of airborne pushbroom imaging systems［J］.Photogrammetric Engineering and Remote Sensing，2000，66（4）：385-392.

［5］张祖勋，张剑清.数字摄影测量学［M］.武汉：武汉大学出版社，1997.

Automatic image segmentation of single linear array image based on dynamic programming

YANG Cheng-min1，2，3，HU Jian1，2，LI Jing-mei1，2
（1.Key Laboratory of Quantitative Remote Sensing Information Technology，Chinese Academy of Sciences，Beijing 100094，China；2.Academy of Opto-electronics，Chinese Academy of Sciences，Beijing 100094，China；3.University of Chinese Academy of Sciences，Beijing 100049，China）

An automatic image segmentation based on dynamic programming which minimizes the error of fitting through mutiple-step searching by using quadratic polynomials to fit the angle elements of exterior orientation in POS data is presented for geometric rectification of the aerial single linear array image in the platform with GPS/IMU.The result of experiment indicated that algorithm can be used for segmentation of image based on change trend of the angle elements of exterior orientation in POS data，and it is feasible for decreasing error of fitting and improving precision of rectification.

single linear array image；dynamic programming；auto segmentation；POS data

TN29

A

1674－6236（2016）03-0156-04

2015-04-22稿件编号：201504236

中国科学院光电研究院创新项目（Y40B08A14Y）

杨成敏（1989—），男，山西阳泉人，硕士研究生。研究方向：数字图像处理。