非匀速运动环境对超声波相位测距影响研究
刘馨宁,黄 宇,孙协昌,李 勐
(航天恒星科技有限公司 北京 100086)
非匀速运动环境对超声波相位测距影响研究
刘馨宁,黄 宇,孙协昌,李 勐
(航天恒星科技有限公司 北京100086)
针对超声波相位法测距应用中测距端运动所造成的多普勒效应对测距超声波传播频率的影响,提出了改进的超声波相位法测距数学模型,其中重新推导了超声波总相位差与空间距离的关系;为了适应普遍情况还对变速运动情况下的产生的多普勒效应进行了详细的分析,并将整个测距波传播过程分为往程、回程两部分,分别讨论每个阶段测距端的运动对测距波传播的影响;实验结果显示在运动条件下测距结果与忽略多普勒效应的原有方法相比有适当提高,表明改进后的超声测距波传播理论模型有效提升了超声波相位法测距准确性。
超声波测距;相位差法测距;回波相位;非匀速多普勒效应;多普勒频移
鉴于近年全世界汽车总量持续增长,针对预防车辆碰撞的相关测距技术的研究价值也在日益凸显[1-2]。在多种测距方式中,超声波测距由于其性能几乎不受粉尘、光线、烟雾、电磁干扰和有毒气体的影响,并且结构相对简单、造价较低、易于使用,因而其在车辆安全行驶辅助系统、工业控制、建筑测量、料位测量、机器人自动导航、无人作战平台、物体识别与定位、地形地貌探测乃至江河水位高度监测等诸多领域都有着广泛应用[3-5]。超声波测距系统主要利用超声波在空气中的定向传播的现象来测量声波的传播距离。目前的超声测距方法主要有飞行时间(即TOF,time-of-flight)检测法、相位差检测法、双频连续波检测法、多频连续波检测法、二进制频移键控方法及有声调频超声波系统等[9-11],其中TOF检测法较为基础的测距技术,原理是通过利用超声波在介质中的传播及反射性质,通过测量测距超声波信号从发射器传播到反射目标再到被接收器接收所用的时间来测定目标与发射端的距离[12-13]。在后续的研究过程中,随着超声波测距的相关理论研究不断完善,提升超声波测距精度逐渐成为超声波测距领域的研究热点,于是随后在TOF的基础上便有了相位差法测距,亦即通过在原有TOF技术测量超声波收发时延的基础上分析波形相位差来有效提升测距精度[14-15]。而相位差法作为双频、多频连续波检测法的理论基础,也具有较强的可研究性,对后续工作中通过理论延伸来提升其他相关测距技术的精度也有较大帮助。
1 超声波相位差法测距及多普勒效应原理
1.1超声波
振动在弹性介质中的传播称为波动,简称波。振动频率在16 Hz-20 kHz之间的机械波,能为人耳所闻,称为声波:低于16 Hz的机械波,称为次声波;高于20 kHz的机械波,称为超声波,而高于100 MHz的机械波,则称之为特超声波。同其它声波一样,超声波的传播速度取决于介质密度和介质的弹性常数。在大气条件下,超声波在同一介质中的传播速度是
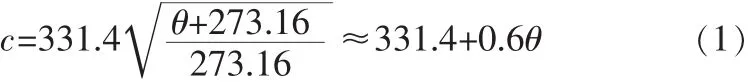
其中θ是空气介质的温度(℃)。
声波是因缘于传播介质中的质点运动而传播的,其传播方向与其振动方向一致,故空气中的声波属于纵向振动的弹性机械波。在理想介质中,描述简谐声波向x正方向传播的质点位移运动方程可表示为:
s(t)=A(x)cos(ωt+φ)=A0e-αxcos(ωt+φ)(2)
式中,s(t)表示质点的位移:A0是振动初始条件决定的常数:ω,t分别表示角频率和传播时间;φ为初相;α为衰减系数。
1.2相位差法测距原理
相位差法测距原理如图1所示(此处以连续波测量系统为例),整个系统由发射测距信号的发射单元、接收测距回波信号的接收单元、测距相关运算的核心部分即相位差测距计算单元以及显示单元所组成。一样的,而且,在相当大的频率范围内,声速是固定不变的。空气中的声波传播速度c可近似地表示为[3]:
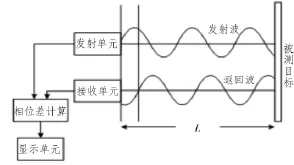
图1 相位差法测距原理图Fig.1 Schematic diagram of phase shift rangefinder
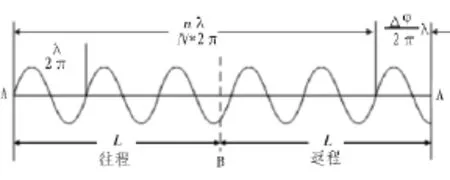
图2 往返波形Fig.2 Round-trip waveform
该系统通过相位计将发射信号(又称参考信号)与接收信号(又称测距信号)进行相位比较,并显示出发射信号在所要测量的距离上往返传播所引起的相位变化φ。如果将调制波的去程和返程展开,则有如图2所示的往返波形。
可测得超声波从发射端A到目标B再到A点的总相移量φ为:
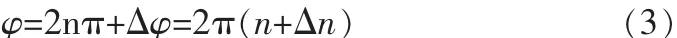
其中Δn=Δφ/2π,波长为λ,超声波频率为f,往返总时延为t,则对于发射端A到接收端B的距离L有:
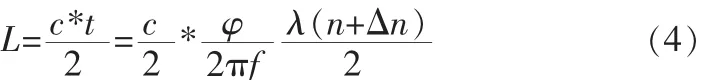
式中t是AB两端传输时间,通过测量出从发出到接收的总相位差可以求出AB间距离。
1.3多普勒效应
在介质中,当波的发射端与接收端存在相对运动时,接收端接收到的振动频率与发射端发出的频率不同的现象即为多普勒效应。多普勒效应可以分为三种情况来分析:发射端静止,接收端运动;发射端运动,接收端静止;发射端接收端均运动。
1)发射端静止,接收端运动

图3 接收端运动情况下的多普勒效应Fig.3 Doppler effect caused by the motion of receiver
接收端运动情况下的多普勒效应如上图所示,其中c为波速,vo为接收端运动速度,A为发射端位置,B为接收端初始位置,B’为经历时长dt后的接收端位置。若接收端静止,则在dt时长内接收端接收到的波为cdt所标示出的部分;由于接收端以速度vo靠近发射端,实际接收端接收到的波形还包括vodt所标示的部分。若发射端发射信号为fo,则有fo=c/λ,又易知接收端接收到的波形频率f=(c+vo)/λ(此处以接收端靠近波源为例),从而可以推导出此时接收端接收到的波形频率与发射端原发射频率的关系为:

2)发射端运动,接收端静止
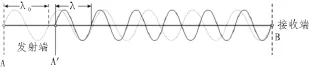
图4 发射端运动情况下的多普勒效应Fig.4 Doppler effect caused by the motion of transmitter
发射端运动情况下的多普勒效应如上图所示,假设发射端以速度vi靠近接收端,A为发射端初始位置,A’为经过时长dt后的发射端位置,B为接收端位置。由于此时发射端与波的传播方向同向移动,在单波长周期T内波源向传播方向移动距离为viT,故实际的波长长度λ=λ0-viT,又由于f=c/λ,波速c不变,可得此时接收端接收到的波形频率与发射端原发射频率的关系为:

3)发射端接收端均运动
综合以上两种情况不难得出当发射端、接收端分别以速度vi、vo相互靠近时接收端接收到的波形频率与发射端原发射频率的关系为:

2 超声波相位差法测距模型分析
2.1往程传播
在本课题所研究的应用中,我们假设车载的超声波测距

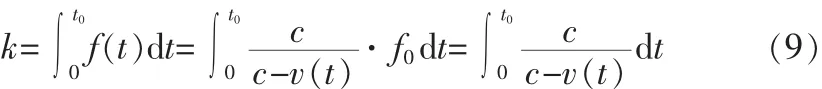
已知总频移φ=2πk,k为波数,在频率一定时,有k=f*t;对于频率随时间变化的情况,可以用f(t)对t积分,也就是将t切成无数微小的时间片(每个时间片内f(t)可以看做是不变的),然后对每个时间片内的频率时长乘积进行求和,故[0,t0]内所传播的波数用公式表示如下:设备是运动的,而目标是静止的,故而在分析往程传播(即超声波从发射端到达目标的波程)时可以借鉴第2节中第(2)种多普勒效应的理论模型。前面提到,为了适应一般情况,这里不再假设发射端相对于目标做匀速直线运动,而是考虑变速运动的情况,此时需要将其运动速度看作关于时间t的函数,即需要将前面分析时的发射端速度v改写为v(t)。
若原发射频率为f0,假设发射端(即测距装置)以速度v (t)接近目标,由公式(6)可知在多普勒效应影响下在t时刻超声波的实时频率为:
可求得[0,t0]内的总相移φ为:
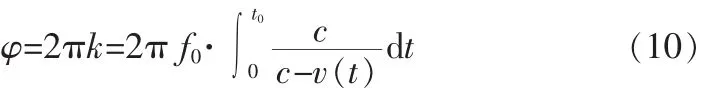
2.2回程传播
往程传播中多普勒效应的主要影响是超声波的波长变化,经过变化的波在到达目标后经过反射即进入了回程传播阶段,此时可以将静止的目标看作是波源,运动中的测距设备作为接收端。由于接收端的运动,其在[0,t0]内实际接收到的波所占空间长度s可表示为(仍以测距设备与目标不断靠近为例):

上式中t1为[0,t0]内测距端接收到的波在传播时所占的时间长度,故由式(10)可知[0,t0]内接收到的波的总相移φ1可表示为:
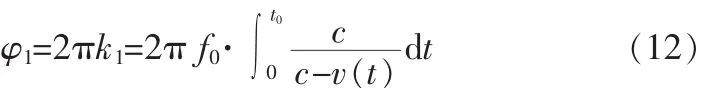

其中v发(t)和v收(t)分别表示该部分波发出时刻和接收时刻测距端的运动速度。
2.3回波相位测距模型
测距信号由测距设备发出、遇目标反射在经测距设备接收的路径总长度与测距设备和目标的初始距离、波速、测距设备移动速度有关,测距波路径如图5所示,其中tA表示整个波程总时延,L表示初始时刻设备与目标的距离。
若以测距波开始发送时刻为0时刻,则在[tA,tA+t0]内测距装置所接收到的波数k1即为:
此时测距端接收到的频率为:


图5 测距波路径示意图Fig.5 Sketch map of wavepath
即k1代表的相移为φ1=2πk1,若忽略多普勒线效应则会认为该部分波所占的空间长度LF为:

而实际应通过先公式(16)求出t1:
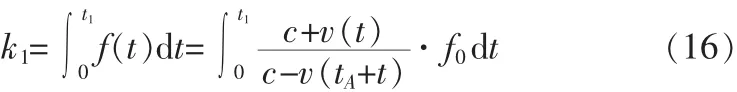
再代入L=c*t1求出L的实际长度。
3 超声波相位差法测距仿真
在仿真阶段首先利用Matlab对不同运动形式下的测距情况进行模拟当测距端分别以匀速、时间一次函数、时间二次函数、时间3次函数接近目标时,测距端接收到的超声波频率与时间关系如图6、7、8、9所示。

图6 匀直运动条件下的多普勒频率Fig.6 Doppler frequency caused by uniform linear motion
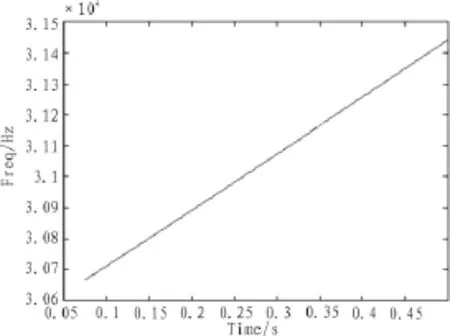
图7 时间一次函数条件下的多普勒频率Fig.7 Doppler frequency caused by uniform accelerated motion

图8 时间二次函数条件下的多普勒频率Fig.8 Doppler frequency caused by motion in which speed is proportional to square of time

图9 时间三次函数条件下的多普勒频率Fig.9 Doppler frequency caused by motion in which speed isproportional to the third power of time
图6~9显示了在测距设备向目标方向以不同速度运动的条件下多普勒效应对接收时超声波频率的影响,频移造成的波长变化使得相位大小与超声波所占空间长度的关系不再恒定,故而会造成相位差法测距的一定误差。通过图10~11可以得知累计波数增大时所产生的距离误差也会增大,即在相位比较时的相位差越大,忽略多普勒效应所造成的距离测量误差也就越大。故而在分析测距回波时,需要考虑测距装置在发射超声波时的运动状态以及测距装置在历经整个反射波程后在接收测距波时的运动状态对测距波波长的影响,从而精确的通过相位差推导该部分波所代表的空间长度。

图10 时间一次函数条件下的频谱图Fig.10 Frequency spectrogram in condition of uniform accelerated motion
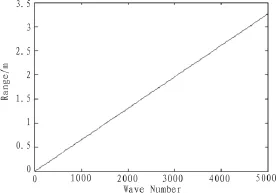
图10 时间一次函数条件下的测距差与波数关系图Fig.10 The relationship between range and wave number in condition of uniform accelerated motion
4 结束语
本文通过分析在超声波相位测距过程中测距端的运动所引起的多普勒效应以及该效应对测距超声波波形的具体影响,重推导了运动状况下超声波相位与空间距离的关系,改进了相位法测距数学模型并通过实验验证了该模型对超声波测距性能的提升。在后续的工作中,会着重研究测距超声波遇到目标后的反射过程对测距波的影响,以及建立针对低速移动目标的探测模型。
[1]Assous S,Hopper C,Lovell M,et a1.Short pulse multifrequency phase-based time delay estimation[J].Journal of the Acoustical Society of America,2010,127(1):309-315.
[2]Cowell D M J,Freear S.Separation of overlapping linear frequency modulated(LFM)signals using the fractional Fourier transform[C].IEEE Trans.Ultrason.Ferroelectr.Freq. Control,2010,57(10):2324-2333.
[3]倪卫宁,朱祖扬,张卫,等.高精度微距超声波测距系统[J].仪表技术与传感器,2013(1):75-76.
[4]温宗周,李富宁,夏自帮.高精度超声波测距系统的设计[J].仪表技术与传感器,2012(11):89-91.
[5]Ka C,G.E.Smid,Z.Pan.Multi-sensor Based Collision Warning System:Proc.of the 32nd ISATA,June l4-18,1999 [C].Vienna,Austria:IEEE Computer Society.
[6]孙传友,孙晓斌.感测技术基础[M].北京:电子工业出版社,2001.
[7]JIANG S B,LIN D Y,LU F M,et al.IEEE Transactions on Instrumentation and Measurement:IEEE Transactions,2009 [C].Columbus,USA:IEEE Computer Society.
[8]韩丽茹.提高超声波测距精度方法综述[J].电讯技术,2010,50(9):132-136.
[9]Huang Y P,Wang J S,Huang K N,et al.Envelope pulsedultrasonic distance measurement system based upon amplitude modulation and phase modulation[J].Review of scientific instruments,2007,78(6):065103-8.[10]Ronald Jurgen.Object Detection,Collision Warring and Avoidance System[M].Washington DC:Society of Automotive Engineers International,1998.
Analysis of the influence on ultrasonic phase rangefinder induced by nonuniform motion
LIU Xin-ning,HUANG Yu,SUN Xie-chang,LI Meng
(Space Star Technology CO.,LTD,Beijing 100086,China)
In this work,the doppler effect on ultrasonic ranging signals induced by the motion of the rangefinder is analyzed, and in the proposed optimized mathematical model,the relationship between the ultrasonic wave phase difference and the spatial distance is derived;in order to accommodate general conditions,the doppler effect induced by non-uniform motion is described,and for convenience of analysis,the propagation of the ultrasonic ranging signals is divided into two parts:forward propagation and backward propagation,and the doppler effect in each part is discussed separately;the simulations show that the optimized ultrasonic ranging method produces better results in comparison with the old method,which indicates that the accuracy of the phase shift rangefinder is improved.
ultrasonic ranging;phase shift rangefinder;phase of echo;doppler effect induced by non-uniform motion;Doppler shift
TN958.94
A
1674-6236(2016)03-0129-04
2015-04-22稿件编号:201504237
总装预研基金项目(9140A21010114HT05064)
刘馨宁(1990—),女,黑龙江哈尔滨人,硕士研究生。研究方向:信号处理,图像处理。

