新型三轴转台模拟卫星飞行解耦方法研究

李松健，白 涛，熊淑杰，林宝军，3

（1.上海微系统与信息技术研究所 上海　200050；2.上海微小卫星工程中心 上海 201210；3.上海科技大学 上海　200031）

新型三轴转台模拟卫星飞行解耦方法研究

李松健1，2，3，白 涛2，熊淑杰2，林宝军2，3

（1.上海微系统与信息技术研究所 上海200050；2.上海微小卫星工程中心 上海 201210；3.上海科技大学 上海200031）

针对某型卫星地面半物理仿真实验，提出一种新型解耦方法，解决在三轴转台的中框旋转至90度附近时，内框与外框重合导致出现奇异性的问题。从角度变换公式入手，分析出现奇异的原因，并对新型方法进行计算、仿真。结果表明，在不能避免三轴转台内框与外框重合的情况下，在以保证三个轴的转速不超出转台最大速度限制的条件下，可以满足卫星的半物理仿真实验要求。

三轴转台；半物理仿真；解耦算法；奇异性

随着我国卫星事业的快速发展，对卫星控制的精度要求越来越高，卫星在地面的半物理仿真实验要求也随之提高。卫星的半物理仿真实验中的一个重要组成部分就是利用三轴转台模拟卫星在太空的三轴角速度，并利用光纤陀螺采集三轴转台数据，反馈给星载计算机，为卫星确定姿态提供数据。卫星的姿态轨道控制工作模式包括太阳捕获模式、对日保持模式、最小安全模式、地球捕获模式、正常工作模式、轨道控制模式和无控模式。光纤陀螺是一种测量卫星三轴姿态角速率的高精度敏感器，它分别工作在太阳捕获模式、对日保持模式、地球捕获模式、轨道控制模式中。

三轴转台由外框、中框、内框组成，分别实现三轴的旋转。由于设计原因，中框安装在外框上，内框安装在中框上。外框带动中框和内框一起旋转，中框带动内框旋转，因此3个转台轴存在耦合关系。当中框旋转导致内框与外框在一个平面上时，转台控制将会出现奇异，内框与外框的转速都会趋向于无穷大。针对在卫星半物理仿真中出现的上述问题，分析转台三轴运动的数学关系，并提出一种新型解耦方法进行仿真。

1　转台速率方式公式推导

在某型卫星的地面半物理仿真测试中，转台三轴与卫星本体系的对应关系如下：

内框（α）正方向：X轴

中框（β）正方向：Y轴

外框（γ）正方向：Z轴

其中，α、β、γ分别为转台内、中、外三框相对转台零位转过的角度。

图1　转台和陀螺坐标系Fig.1　Coordinate system of turntable and gyro

陀螺安装于三轴转台内框台面上，当转台处于正交状态时，转台内框的三轴角速度应为卫星本体角速度。随着三轴位置的变化，转台三轴的角速度需要通过转换公式投影到安装在内框卫星本体“内框三轴”上，三轴角速度投影到“内框三轴”上的结果为［1-2］：

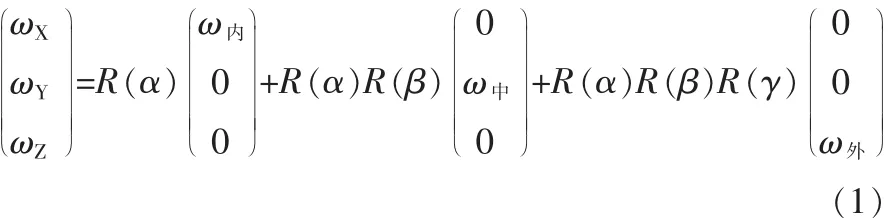
其中，ωX、ωY、ωZ为卫星本体角速度，ω外、ω中、ω内为转台三轴旋转角速度，

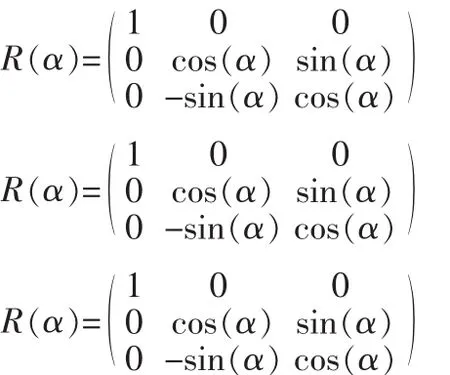
地面进行仿真时，利用转台模拟卫星真实角速度，将陀螺安装于转台敏感转台角速度，并将测量输出引入仿真闭环。此时需要在驱动转台时考虑地速影响，使陀螺的测量输出真实反映卫星角速度。

进行仿真时，转台零位设置如下：

内框正方向：Xb轴→北

中框正方向：Yb轴→西

外框正方向：Zb轴→地

转台处于零位时，地速在“内框三轴”上的投影为：

其中，λ为当地纬度，ωe为地速的模值。当转台转到任意位置时，地速在“内框三轴”上的投影为：

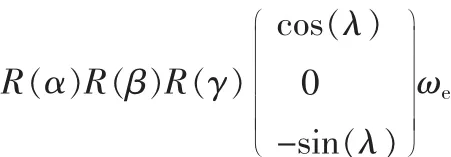
考虑地速影响后，

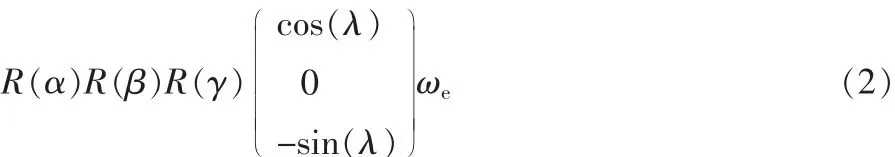
化简方程（2）得：

经过计算可得：

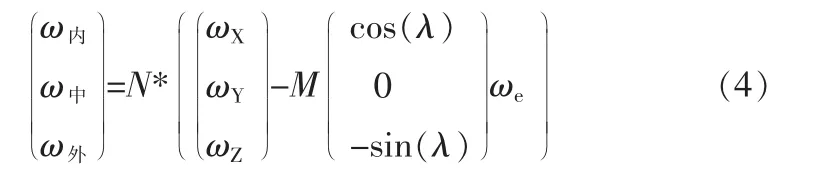
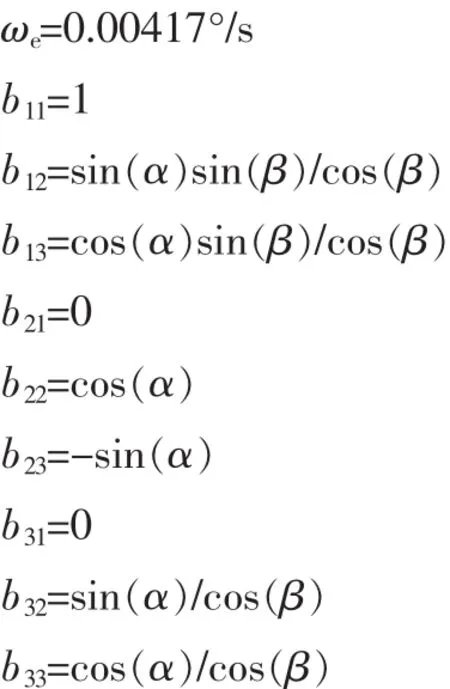
其中 ωe内、ωe中、ωe外分别为地球转速对内、中、外三轴的影响。

由上述公式推导可知，当内框转到90度时，cos（β）=0，ω内与ω外分别趋向于无穷大。因此当内框与外框重合时，转台无法模拟卫星的运动。

2　传统处理方法与仿真分析

针对由于中框旋转导致内框与外框重合的问题，传统的解决方式是避免转台转角过大而使转台产生耦合［3-6］。由于在卫星运行中，卫星的俯仰角速度为快变量，卫星的滚动角速度和偏航角速度为慢变量［7］，用转台外轴模拟卫星的俯仰轴，内轴和中轴分别模拟卫星的滚动轴和偏航轴。这样的设计虽然可以在大部分时间避免转台内框与外框重合的问题，但是对于在半物理仿真中模拟卫星初始入轨阶段的大机动姿态变化则不能满足测试要求。

在Matlab中模拟卫星大角度机动的三轴角速度。为了方便观察，设置卫星三轴角速度均为2°/s。在避免转台中框与外框重合的前提下，转台中轴的转角范围为-88°至88°，转台内轴的转角范围为-180°至180°。所得结果如图2～4所示。

图2　不同内、中轴转角的内轴角速度Fig.2　Inner axis velocity with various inner、middle axis angle

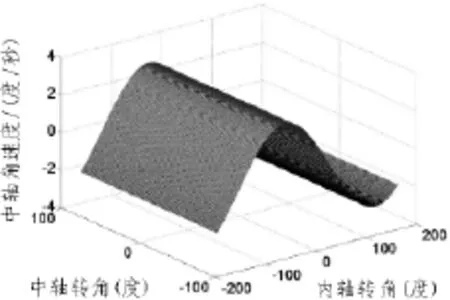
图3　不同内、中轴转角的中轴角速度Fig.3　Middle axis velocity with various inner、middle axis angle

图4　不同内、中轴转角的外轴角速度Fig.4　Outer axis velocity with various inner、middle axis angle

由图2至4可知：中轴转角对中轴角速度没有影响，中轴角速度随着内轴转角的变化而呈正弦规律变化。内轴与外轴角速度与内轴、中轴转角均有联系，当中轴转角旋转至接近时，内轴与外轴的角速度快速上升，转速均超过三轴转台的转速允许范围，在实际的半物理仿真实验中造成转台报警，进而强制转台停止运转。

3　改进的解耦方法

对于一些不能避免转台内框与外框重合的情况，采用分类设计的思想，在正常区域转台根据半物理模型输出的数据正常运行，在奇异点的区域采用限制外轴、内轴转速的方式最大限度地使转台准确模拟卫星姿态，并且平稳度过奇异点区域。

因为地球转速很小，所以在不考虑地球转速的情况下，简化公式（5）得到公式（6）：

可以看到，中框的角速度与中框的转角β无关，仅仅与内框的转角α有关。内框与外框的角速度与内框转角α和中框转角β均有关系，而且当β趋向于±90°时，ω内、ω外均趋向无穷大。本型号卫星地面测试三轴转台最大转速为100°/s，最大的角加速度为50°/s2。卫星本体角速度ωX、ωY、ωZ均为2°/s。根据，因此当α=45°，β=88.4°时就转台的外轴和内轴就达到100°/s。

根据转台的技术参数以及安全考虑，当转台的中框转角在85°至95°（或者-85°至-95°）区间时，限制内轴与外轴转速不超过50°/s，等待中框旋转出这一区域后再采用正常运行模式。

4　仿真与分析

为了模拟姿态控制过程中的卫星姿态，地面半物理仿真测试引入卫星的动力学数学模型。动力学数学模型将卫星的姿态数据传送至各个测试设备以达到模拟卫星在太空中姿态变化的目的。

本次仿真测试采用U（外轴）、O（中轴）、T（内轴）形式的三轴高精度转台。通过光纤反射器将动力学模型输出的卫星三轴欧拉角速度数据输入至三轴转台。通过三轴转台的控制软件观测得到的转台三轴角速度如图2至图4所示。

图5　内轴角速度与时间关系Fig.5　Relation between velocity of inner frame and time

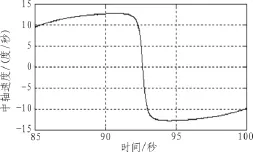
图6　中轴角速度与时间关系Fig.6　Relation between velocity of middle frame and time

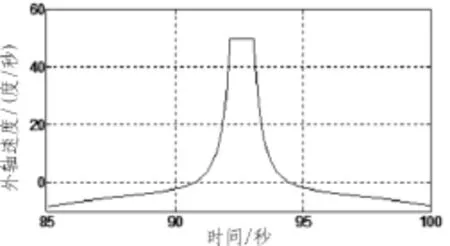
图7　外轴角速度与时间关系Fig.7　Relation between velocity of outer frame and time

由图5至图7可知，在仿真时间90秒至95秒期间，内轴与外轴角速度快速变化，在93秒至94秒期间，内轴与外轴角速度超过50°/s，根据程序预先设置，内轴与外轴速度被限制在50°/s。转台控制器没有启动保护机制，三轴转台处于可控运行状态。由图6可知，转台中轴也因内轴、外轴转速的限制产生快速变化，中轴的变化较内、外轴平缓而且没有超出50°/s。

内轴与外轴的限速阶段只有约1秒的时间，对半物理仿真的影响可以忽略。最重要的是解决了中轴旋转至附近，内轴与外轴超速导致转台停转，引起半物理仿真试验停止的问题。

5结论

该解耦算法针对卫星半物理仿真中三轴转台的中框转至附近时内框与外框旋转出现奇异的问题，提出在奇异点附近对转台进行限速的方案，实现了在进行大角度仿真试验中转台连续运行。仿真结果表明在转台限速的条件下，转台三轴均可以正常运行并且限速时间短，对半物理仿真影响较小。

［1］王海峰，王成良.解决欧拉方程奇异性的方法研讨［J］.飞行力学，2006，24（3）：94-96.

［2］章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998.

［3］江华，刘利.三轴仿真转台系统的动力学建模与耦合分析［J］.弹簧与制导学报，2005，25（1）：255-257.

［4］刘延斌，金光，何惠阳.三轴仿真转台系统模型建立及解耦控制研究［J］.哈尔滨工业大学学报，2003，35（3）：323-326.

［5］黄卫全，刘文佳.三轴仿真转台解耦问题的研究［J］.弹簧与制导学报，2009，29（1）：99-103.

［6］叶立军，王静吉，朱文山.转台高精度模拟卫星三轴角速度解耦算法研究［J］.上海航天，2014，31（3）：15-19.

［7］黄华红，杨云川，吕艳慧.一种鱼雷俯仰角出现时的姿态仿真方法［J］.鱼雷技术，2012，20（3）：20-23.

A novel research on decoupling algorithm of turntable simulating satellite’s flight

LI Song-jian1，2，3，BAI Tao2，XIONG Shu-jie2，LIN Bao-jun2，3
（1.Shanghai Institute of Microsystem and Information Technology，Shanghai 200050，China；2.Shanghai Engineering Center for Microsatellites，Shanghai 201210，China；3.Shanghai Tech University，Shanghai 200031，China）

In allusion to the satellite attitude and orbit control semi-physical simulation system，a new decoupling algorithm of the turntable was put forward，which solved the singular problem caused by the overlap of middle frame and outer frame when inner frame turn to 90 degrees.Started with the angle reforming formula and figured out the reason of singular phenomenon，calculated and simulated the novel method.The result showed that when the overlap of middle frame and outer frame is unavoidable，the requirement of semi-physical simulation was satisfied in the case of unexceed the speed limit of three axes.

three-axes turntable；semi-physical simulation；decoupling algorithm；singular problem

V416

A

1674－6236（2016）03-0072-04

2015-08-11稿件编号：201508051

中国新一代卫星导航系统重大专项工程

李松健（1990—），男，黑龙江哈尔滨人，硕士研究生。研究方向：卫星地面测试，控制与仿真。