基于改进模糊贴近度算法的钻井平台泵系统故障诊断

温娜，杨奕飞

（江苏科技大学 电子信息学院，江苏 镇江　212003）

基于改进模糊贴近度算法的钻井平台泵系统故障诊断

温娜，杨奕飞

（江苏科技大学 电子信息学院，江苏 镇江212003）

针对深水钻井平台监控环境复杂的特点，为了提高钻井平台泵系统故障诊断的准确性和有效性，本文研究一种基于改进模糊贴近度算法的故障诊断方法，对传统的模糊贴进度公式做了一定的改进。以模糊贴近度原理为基础，再结合模糊数学隶属度的概念，搭建出了一种新的模糊贴近度函数模型。通过实验数据的验证，经过改进后的模糊贴近度算法比传统的模糊贴近度算法更加有优势，能够很好的进行深水钻井平台上钻井泵机系统的设备故障诊断任务。

模糊数学；贴近度；钻井泵系统；故障诊断

随着海洋油气资源的持续开发，深水钻井平台得到了越来越多的应用，钻井泵作为钻机的心脏，起着关键的作用。钻井泵一般处于较差的环境、有着较高冲击负荷的地方，所以其上的设备零部件要有很高的强度和精准的装配精度［1］。如果发生故障，不仅影响钻井生产，更会造成钻井平台的整体故障，因此对于泵系统的实时监测与故障诊断具有非常重要的意义［2］。

一般现有的故障诊断有3种方法：第一，基于数学建模的方法；第二，基于信号处理的方法；第三：基于人工智能的方法。较为常用的是第三种方法，且是基于神经网络的人工智能法。但是这种方法在诊断之前必须使用一定量的故障样本来训练对神经网络，而大量的故障样本很难得到，为此文献［3］提出一种贴近度的模糊模式识别方法，该方法使用模糊贴近度理论把已经诊断的故障数据和从系统中测得的需要诊断的故障样本进行一个模糊贴近度的对比，经过比对后查明故障起因，这样可以有效地对设备的各方面进行故障诊断。但是这种方法会对于一部分的故障可能会出现错误诊断的现象。

针对以上几种方法的缺点，文中研究一种基于改进模糊贴近度算法的钻井泵系统故障诊断，以模糊贴近度原理为基础，再结合模糊数学隶属度的概念，搭建出了一种新的模糊贴近度函数模型，并结合深水钻井泵的特点实现泵系统诊断的准确性和有效性。

1　模糊贴近度原理

1.1贴近度的概念

贴近度就是衡量两个模糊集合间密切程度的方式，其值的范围在［0，1］之间。如果其值接近0，说明这两个集合间的距离远，两者之间的关系比较疏远；而当值接近1的话，说明它们之间距离小，两者间的关系就会更加密切［4］。用数学语言表述为：设论域U，映射n：F（U）。F（U）→［0，1］满足条件：

1）n（A，A）=1，n（φ，U）=0

2）n（A，B）=n（B，A）

3）A⊆B⊆C→n（A，C）≤n（A，B）∩n（B，C）

则称n（A，B）为A与B的贴近度。

1.2传统贴近度

常见贴近度求取公式如下：

最小最大贴近度：

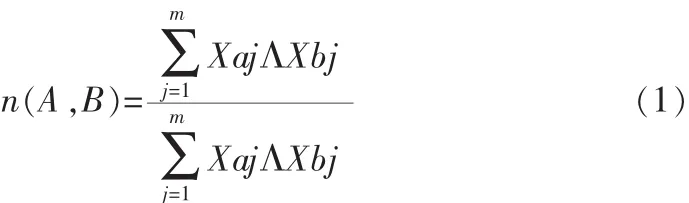
式（1）中：j为样本中的特征值个数，j=1，2，…，m

Xaj是需要测试的故障样本a中的数据，Xbj则是标准故障样本b中的数据，∧是取小运算，∨则是取大运算。

使用传统的贴近度求取公式能够获得模糊集合的贴近程度如何，但在计算的过程中会有一些不足之处：利用式（1）在有的情况下得不到预想的结果，下面用两组泵转速标准故障数据举例说明：

转子不平衡振动 A=（1，0.8023，－0.027，0.5493，0.5556，0.4，－0.7059，0.631）；

转子间不对中振动B=（－0.504，－0.6279，－0.9243，－0.5493，－0.5556，－1，1，－0.93）。

由贴近度的求取公式算得的两组数据的贴近度是－1.18036，其结果不在贴近度的合理取值范围内，不能够正确的诊断故障。所以为了减小传统贴近度算法的失误率，在本文中以模糊贴近度的原理为依据，再其基础上结合了模糊数学的隶属度概念，对以往的贴近度公式的不足之处做了相关修改，使得改进后的模糊贴近度对故障能够达到更好的识别效果。

2　改进的贴近度

2.1隶属函数的定义

隶属函数的定义为：如果集合U的任一元素都有集合A中的1个数且元素唯一，即A（x）∈［0，1］和之相对应，那么集合A就称之为集合U上的模糊集合，其中A（x）就是元素x对集合A的隶属度［5］。当x在集合U中改变时，相应的A（x）也会改变，两者之间就对应了一种函数关系，这种函数关系就称为集合A的隶属函数。A（x）越靠近1的时候，表明元素x是U元素的程可能性越大；相反，如果A（x）靠近0时，说明x为U中元素的可能性越小。所以其是用取值和区间［0，1］的隶属度函数A（x）来表示x属于集合U的程度高低。

2.2归一化

隶属度函数的选取好坏会直接关系到系统故障诊断时的准确性和稳定性［6］。在故障诊断系统中，很多的潜在故障都是一些会在系统运行时，直接决定整个系统安全可靠运行的，其都会具有报警阀值，所以在进行隶属度函数换算前要对潜在征兆数据做归一化处理，即是对

样本进行标准化，

在公式（2）中：x代表的是征兆数据偏离正常值的程度大小；v0是运行过程中不会导致报警的正常值，是经运行过程所得；va是在运行过程中获得的故障数据；vb则是参照标准值，是已经经过诊断的标准故障样本值。

2.3隶属度函数构造

因为在钻井平台的故障诊断系统中，故障会存在偏离正常状态值较大范围或仅在正常值附近范围变动，而且不同的故障对相应的征兆的密切程度也不相同，因此在本文中依据以上的条件和隶属度函数的普遍适用性，再结合钻井平台上故障的特点，构造了更加精确的隶属度函数：

新构造的隶属度函数拥有两个新的特点：第一点就是在x=0和x=1的时候函数的变化很小，而当x=0.5时函数变化程度很大，这就表示当故障征兆和正常值靠近时或者等于某个故障值的时候，其变化程度都比较小，函数的这种变化趋势表明了钻井平台上设备的各部分故障征兆的波动情况，基于此，第一个特点对模糊模式的识别非常有利。另一个特点就是若x=0，u（x）=0，而x=1时，u（x）=1，构造这种特点是使故障征兆能够在正常值附近进行浮动变化。所以使用公式（3）的隶属度函数转换以后，可以使用不同的值来表示偏离正常值不同范围的故障征兆［7］。

改进后的贴近度公式是根据距离型的模糊贴近度得到的，贴近程度是通过计算比较待测故障数据值与已知明确原因的故障数据值来确定的，在原则上采用了择近原则，公式如下：

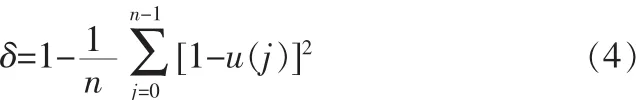
公式（4）中，n代表的是特征值的个数，u（j）代表第j个特征值的隶属度值。

3　算例分析

转子振动波形可以很好的表示钻井泵机系统的工作情况，此外因为转子振动波形的重要信号都可以从其波形上获得，所以就直接的从波形图上获得其特征值为例计算其贴近度。如下的特征参数［8］：振幅（x0）、振动频率（x1）、转子相位角（x2）、上升沿宽度（x3）、波形宽度（x4）、最大余波宽度（x5）、波形面积（x6）、转子转速（x7），这些参数可以非常好的表明空气压力波形的特征，将这几个特征值组合一个集合，即X（x0，x1，x2，x3，x4，x5，x6，x7）。

3.1诊断流程

在深水钻井平台上的故障诊断流程是在开始的时间段内没有故障数据出现的时候，工作人员在出现故障情况以后排查获得故障原因后和故障特征值相对应，当生产过程中产生一定量的故障样本以后，再使用模糊贴近度模型对生产设备的故障征兆进行判断。

所以使用改进后的模糊贴近度诊断故障的流程图如图1。

3.2新旧贴近度比较

表1列出的是钻井系统中泵机系统中的几种普遍故障及其各自的特征值［8］，把采集到的潜在故障数据和这些特征值做贴近度的对比，能够很好的对潜在的故障进行判断。使用这5种样本数据，分别通过传统贴近度和改进后的贴近度公式计算，比较各自诊断的结果。

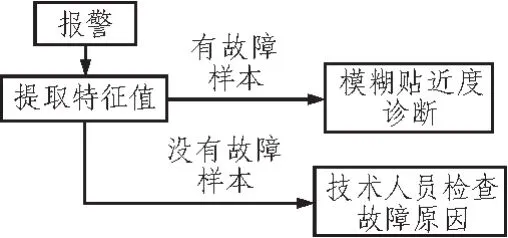
图1　诊断流程图Fig.1　Diagnostic flowchart

样本1：转子不平衡振动（1，1，－0.0703，0.7324，0.1111，0.8，－0.8824，0.5998）；

样本2：转子间不对中振动（1，－0.5698，－0.8595，0.7746，－0.3333，0.6，－0.4706，－0.0649）；

样本3：泵转子滑动轴承涡动（－0.632，－0.5349，－0.8811，－0.6761，－0.7778，－1，1，－0.93）；

样本4：电机轴承磨损（0.232，－1，0.2216，0.1831，－0.1111，－0.2，－1，－0.3672）；

表1　故障及各特征各参数Tab.1　Faults and each characteristic parameters

样本5：泵内部转子、定子之间相对摩擦（1，1，－0.3946，0.7465，－0.3333，0.6346，－0.8824，0.7532）；

在表2中贴近度1表达的是和转子不平衡振动的相似度，贴近度2是与转子间不对中振动的相似度，贴近度3，4，5类推。通过传统和改进的两个公式诊断的结果如下。

表2　传统与改进贴近度计算结果Tab.2　Traditional and improved closeness calculation results

在表2中用下划线标出了最大贴近度的数值，用来判断故障类型。从表2中能够得出，用传统的方法没办法很好的诊断故障，其计算结果容易不在贴近度的取值范围内，有明显的局限性，只可以得到一些变化小的数据。通过比较可以看出修改后的贴近度模型可以比较好地避开这种问题，可以对这些故障征兆数据进行比较好地分别，并且所得的结果和实际相符。在实际应用的过程中，除了对同一种故障进行识别还需要对不同类别的故障进行识别。下面对不同故障的识别进行分析。

转子不平衡振动A=（1，1，－0.5243，0.6901，－0.1111，0.8，－0.7059，0.6736）；

转子间不对中振动B=（－0.504，－0.6279，－0.9243，－0.549 3，－0.5556，－1，1，－0.93）：

通过传统公式（1）算得贴近度δ=－1.28017不能正确辨别故障类型；

通过改进后公式（4）算得贴近度δ=0.30066，可以准确辨别故障类型。

而比较同一种故障两组数据的贴近度如下：

转子不平衡振动A=（1，1，－0.5243，0.6901，－0.1111，0.8，－0.7059，0.6736）；

转子不平衡振动 B=（1，1，－0.0703，0.7324，0.1111，0.8，－0.882 4，0.5998）；

通过传统公式（1）算得δ=0.726397，

通过改进后公式（4）算得δ=0.876867。从算得结果可以看出改进后的贴近度公式可以更加准确的辨别故障类型。

所以由上面的两组数据对比可以看出，改进后的贴近度公式可以很好地识别不同的故障类型，还可以更加准确地辨别相同的故障类型。

依据模糊理论［9］来计算生产过程中实时测得的钻井泵机系统的故障征兆数据与故障标准值之间的模糊贴近度，本文采用Labview编程来实现这个算法。在验证这个算法的可用性时，需要使用已经发生故障的大量样本数据进行验证。下面对钻井泵系统中常见的五种故障各选其中的3组样本进行验证，计算结果如表3。

表3中5种故障样本A，B，C，D，E分别对应的是转子不平衡振动，转子间不对中振动，泵转子滑动轴承涡动，电机轴承磨损，泵内部转子、定子之间相对摩擦的故障样本。在表中给出了经过计算以后的最大贴近度值，经过比较可以看到对故障的诊断结果和实际的泵系统故障情况相符度很接近，表明了改良以后的算法可以很好地辨别不同种类的故障，还可以更准确地辨别相同类别的故障。

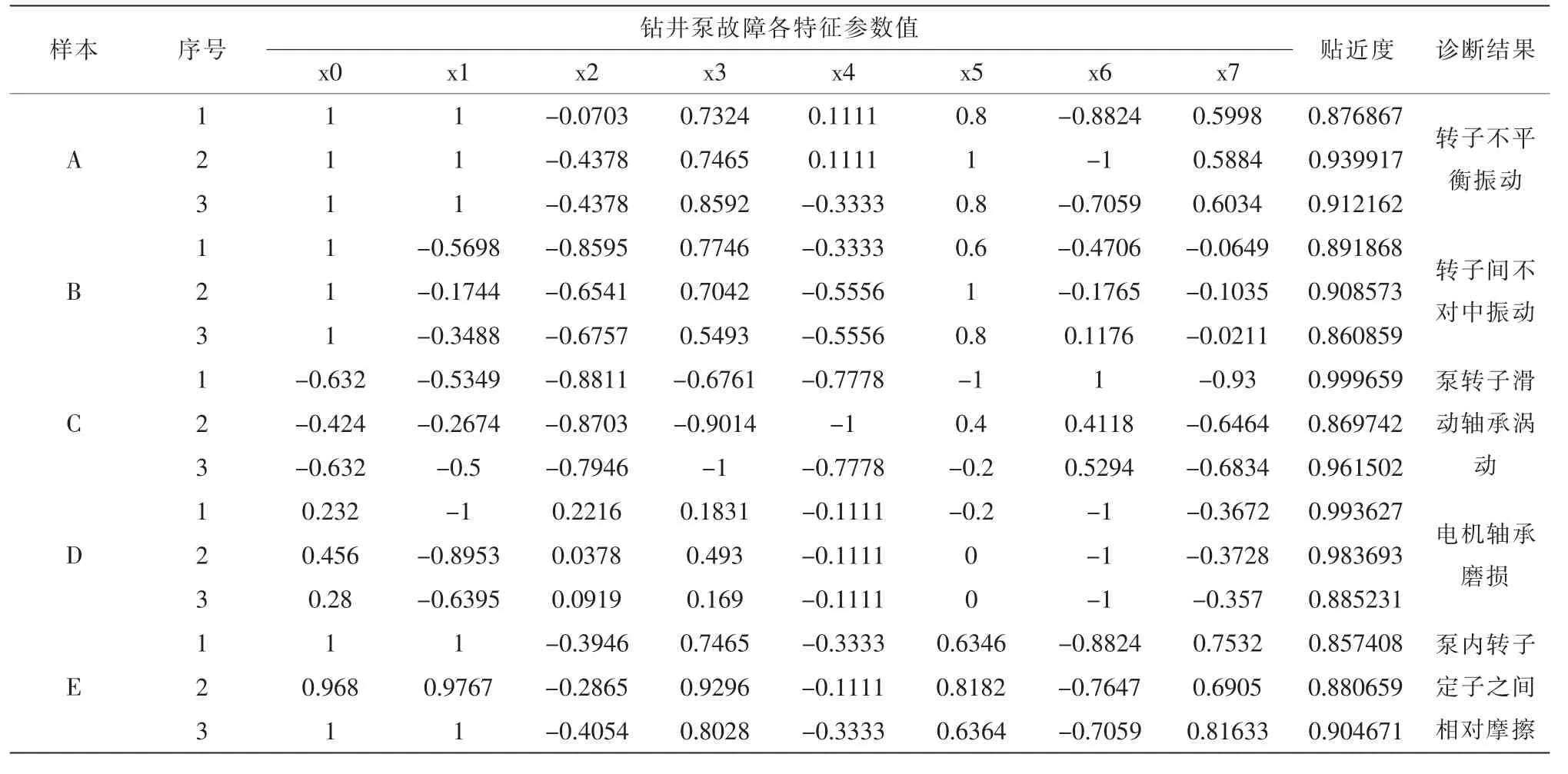
表3　改进贴近度实例计算结果Tab.3　Improved nearness example calculation results

4　结　论

深水钻井平台具有系统复杂、功能多样、工作环境恶劣等特点，容易导致设备出现故障，且故障诊断困难。本文针对平台上重要设备钻井泵机的特点，提出一种改进模糊贴近度算法并应用到深水钻井泵系统故障诊断中，该方法对系统中实时监测到的故障样本可以准确快速的进行模糊模式的辨别，从试验的结果可以得到，使用这种改进后的方法诊断故障得到的数据结果明显优于传统的贴近度算法。同时，该方法可以方便的在基于Labview编写的平台上实现，所以在深水钻井平台上的故障诊断中有着很好的实用价值。

［1］爨莹.基于灰色理论的抽油井泵功图诊断技术研究［J］.微电子学与计算机，2005，22（3）：77-80.

［2］陈阁，马云鹏，罗军，等.钻井泵主要故障诊断与分析［J］.甘肃科技，2009，25（17）：78-80.

［3］黄小龙，刘维亭.基于模糊贴近度的故障诊断［J］.科学技术与工程，2012，12（30）：8111-8115.

［4］Li Hongkun，Ma Xiaojiang，He Yong.Diesel Fault Diagnosis Technology Based on the theory of Fuzzy Neural Network Information Fusion，2003：1394-1410.

［5］眭志方，张冰，朱志宇，等.模糊聚类和模糊模式识别在目标识别中的应用［J］.电光与控制，2007（14）：35-38.

［6］R.Isermann，A.Schwarte.Fault Diagnosis of a Turbocharged Diesel Engine with Dynamic Neural Networks and Parity Methods.Intelligent Systems and Control.2004：446-451.

［7］黄勇.FFNN在柴油机燃油系统故障诊断中的应用［D］.大连：大连理工大学，2008.

［8］刘继宗，时云霞.水泵故障检测技术及应用实例研究［J］.中国科技博览，2011（34）：99.

［9］王鹏，王婧，杜卫东.减影提取焊缝缺陷算法［J］.西安工业大学学报，2013（10）：856-860.

Falut diagnosis of the deepwater drilling platform pump system based on improved fuzzy nearness algorithm

WEN Na，YANG Yi-fei
（School of Electronics and Information，Jiangsu University of Science and Technology，Zhenjiang 212003，China）

Becauase of the complex characteristics of the deep-water drilling platform monitoring environment in the deepwater，in order to improve the accuracy and effectiveness of rigs pumping system fault diagnosis，so this paper reseaches a method of fault diagnosis based on improved fuzzy nearness algorithm.The method improves the formula of the traditional fuzzy nearness.According to the principle of fuzzy nearness，combining fuzzy membership degree，this paper constructes a function model of fuzzy nearness.Experimental data showes that the improved algorithm is superior to the traditional algorithm of fuzzy nearness，and it can also achieve the fault diagnosis of the deepwater drilling pump system effectively.

fuzzy math；nearness；drilling pump；fault diagnosis

TN05

A

1674－6236（2016）03-0065-04

2015-03-18稿件编号：201503240

江苏省产学研联合创新资金资助项目（BY2013066-01）

温 娜（1990—），女，江苏睢宁人，硕士研究生。研究方向：海洋钻井平台系统监测与控制，计算机控制与应用等。