基于压缩感知的语音编码新方案
许佳佳
(陕西师范大学 计算机科学学院,陕西 西安 710119)
基于压缩感知的语音编码新方案
许佳佳
(陕西师范大学 计算机科学学院,陕西 西安710119)
根据语音信号的稀疏性,将压缩感知理论应用于语音信号的处理中,提出了一种语音编码的新方案。该方法在编码端采用随机高斯矩阵对语音信号进行观测,得到较少的观测值,然后使用矢量量化编码进一步压缩数据;在解码端,通过矢量量化解码得到观测值,根据语音信号在离散余弦域中的稀疏性,用正交匹配追踪算法重构语音信号。所用算法,在保证语音信号重构质量的前提下降低计算复杂度,减小时延。实验结果表明,对于采样率为44 100 Hz,量化位数为16 bit,码速率为705.6 kbps单声道语音信号压缩到100 kbps左右仍具有较好的语音质量,同时算法时间延迟低。
压缩感知;离散余弦变换;矢量量化;正交匹配追踪
近几年由D Donoho、E Cand s及华裔科学家陶哲轩等人提出的压缩感知(Compressive Sensing,CS)理论[1-3]指出,只要信号满足可压缩条件或者在某个变换域是稀疏的,就可以用一个与变换基不相关的矩阵对原始信号进行观测,观测得到的信号维数远远低于原始信号按照奈氏采样得到的维数,接收端根据观测得到的少量数据,通过求解优化问题可以高概率的近似无失真的恢复出原始信号。这就突破了奈奎斯特采样定理。该理论一经提出,就成为了信号处理领域的研究焦点。
目前,压缩感知理论的应用研究已经涉及到众多领域[4],如:CS雷达、DCS(Distributed Compressed Sensing)理论、无线传感网路、图像采集设备的开发、医学图像处理、生物传感、光谱分析、遥感图像处理等。在语音信号处理方面也不例外,由于语音信号具有良好的稀疏性,压缩感知应用于语音信号处理的研究也十分活跃。就语音编码方面来看,现行的语音编码方案中CD采用的PCM编码有最高的保真度,但其双声道下1411.2 Kbps的码速率过高,冗余过大;而现在互联网上广泛采用的MP3编码在相对于PCM编码压缩10~12倍时仍具有较好的声音质量,不过其明显的不足是会出现明显的高频丢失,听觉感受上仍有瑕疵,这是因为MP3编码是利用了人耳听觉特性的有损编码的缘故。那么将压缩感知应用于语音压缩编码,可以实现无损压缩。而且压缩感知理论实现了将信号处理中的采样和压缩合二为一,不用高速采样,不用保留大量冗余数据再压缩。这具体会对语音编码带来哪些好处,本文就此进行了研究。
1 压缩感知基本原理
1.1信号的稀疏性
已知离散信号x=[x1,x2,…,xN]T,其可以在RN空间的一组正交基Ψ=[φ1,φ2,…,φN]上分解,其中φi(i=1,2,…,N)是N维向量。则x可以表示为:

其中s=[s1,s2,…,sN]T。
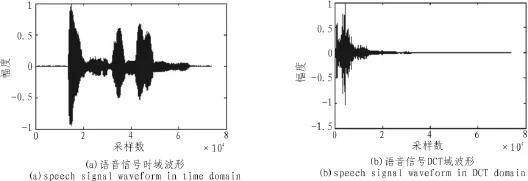
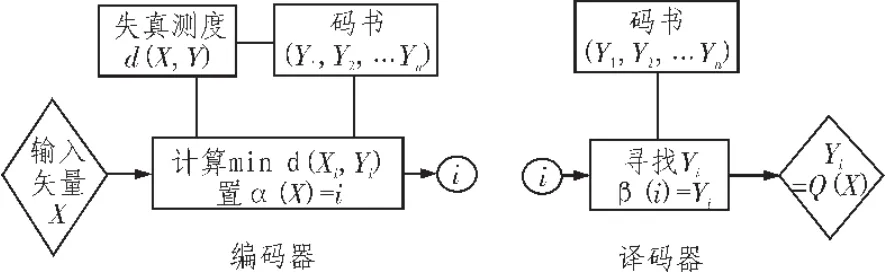
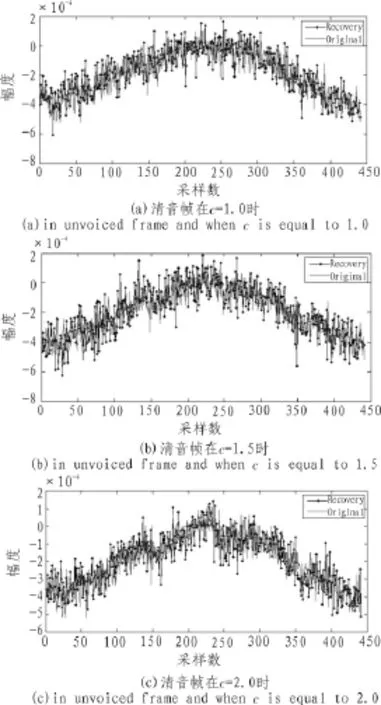
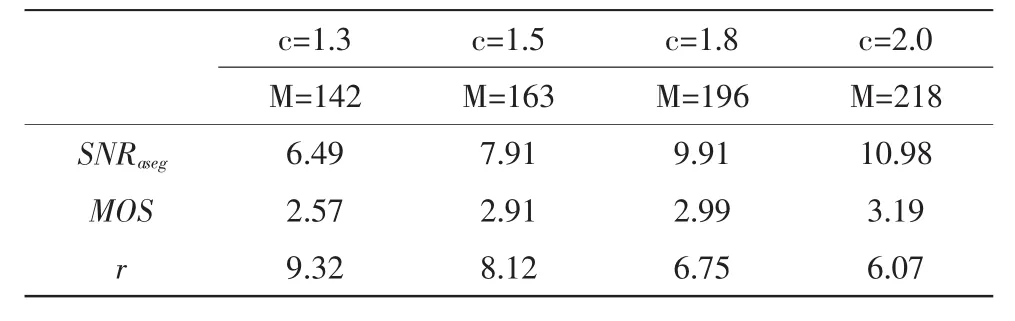
如果‖s‖0=K,且K< 1.2观测与重构 设观测矩阵为M×N的矩阵Φ,观测后所得的向量为y= [y,y,…,yM]T,则压缩感知的数学表达式为, 其中ACS=ΦΨ称之为CS矩阵。 理论上应使Φ与Ψ组成的CS矩阵ACS满足任意2K列都线性无关,即满足有限等距性质(Restricted Isometry Property,RIP)。然而,判断给定的A是否具有RIP性质是一个组合复杂度问题。为了降低问题的复杂度,文献[6]指出如果保证观测矩阵Φ和稀疏基Ψ不相干,则ACS在很大概率上满足RIP性质。 一般地,若s是K-稀疏的,只要M≥cKlog(N/K)(c是常数),就可以由M个方程解出K个未知数。由于K个大系数在s中的位置不确定,该问题的解决就归结为寻求最优解,理论上可以通过l范数优化的方法获得,即 但式(3)的求解是一个NP难的非凸优化问题。 2006年,陶哲轩和E Cand s证明了在RIP条件下l1范数优化问题与l0范数优化问题有相同的解,即 这是一个凸优化问题,可以通过线性规划求解。 语音信号是短时平稳的复杂信号,就单一正交基,一般认为离散余弦变换对语音信号的稀疏效果较好。对语音信号进行离散余弦变换后,大部分能量集中在低频部分,且大多数系数的绝对值都很小,具有近似稀疏性,又由于离散余弦变换具有很强的去相关性,所以本文用离散余弦变换对语音信号进行稀疏分解。 一维DCT的变换矩阵为 M为语音信号长度。 如下,是对取自中科院自动化所语音库中的语音信号进行的稀疏变换。原语音为女声的“二十万纳米”的发音,采样频率为44 100 Hz,采样值的编码位数是16 bit,双声道。实验时取一个声道的数据。 图1 语音信号的时域和DCT域波形Fig.1 Speech signal waveform in time domain and DCT domain 3.1系统描述 该系统先用高斯随机矩阵对语音信号进行CS观测,得到的观测值采用矢量量化编码,经过广义信道传输后,对接收到的信号进行矢量量化解码得到CS观测值,通过OMP算法重构出语音信号。如图2所示。 图2 系统框图Fig.2 System block diagram 3.2语音信号的CS观测 在稀疏变换基选用一维DCT变换矩阵时,依前文所述,只要保证观测矩阵与其不相干,则Acs在很大概率上满足RIP性质,从而保证语音信号可以重构。不过很大概率仍然是个不确切的说法,就具体某观测矩阵是否可以用于压缩感知,E Cande s和Tao在文献[7]中给出了确切的标准。即,对于任意k稀疏信号x∈RN,若存在常数0≤δk<1,使得: 成立,则认为矩阵Φ满足RIP性质。 从语音信号的重构效果及计算复杂度两方面考虑,文中选择高斯随机矩阵作为观测矩阵。 3.3语音信号的CS重构 目前,重构算法主要分为贪婪追踪算法和凸优化算,其他的还有组合算法和基于贝叶斯框架[8]的重构算法。每种算法都有其优缺点,需要结合具体情况选用合适的算法。用凸优化算法重构信号所需的观测次数最少,但计算复杂度高;贪婪追踪算法要求相对更多的观测次数,但计算复杂度低,重构效率高。综合语音编码系统对编码质量和时延性的要求,本文选择贪婪追踪算法中的正交匹配追踪算法 (Orthogonal Matching Pursuit)OMP。 OMP算法的步骤如下: 输入:观测矩阵Φ,稀疏变换矩阵Ψ,观测向量y,稀疏度K;终止条件,一般为最大迭代次数或残差不大于某一值; 输出:信号的逼近xˆ,残差r; 步骤1:初始化,令迭代次数n=0,残差r0=y,重构信号x0= 0,索引矩阵T为空; 步骤2:求CS矩阵Acs的列向量和当前残差rn的投影系数 (内积值)φ,记录最大投影系数对应的位置,即求k=arg 步骤3:更新CS矩阵,令Acs的第k列为零;更新索引矩阵令Tn+1=Tn∪φk,其中φk为原Acs的第k列; 步骤5:判断是否满足迭代终止条件,如果不满足,则转到步骤2,满足则停止迭代。 3.4矢量量化编码 矢量量化是先把信号序列的K个连续样点分成一组,形成K维欧氏空间中的一个矢量,然后对此矢量进行量化[9]。矢量量化过程可定义为K维信源空间χ到其中一个有限子集,即码本Y={Yi|Yi∈χ,i=1,2,…,L}的一个映射Q:Q{X|X∈χ}=,其中,L是码字的个数。矢量量化器的基本工作原理如图3所示。 图3 矢量量化原理框图Fig.3 Block diagram of the vector quantization 实验中的训练语音和测试语音均取自中科院自动化研究所的CASIA语音库,采样频率为44 100 Hz,量化编码为16 bit。根据语音信号的短时平稳性,先对语音信号进行分帧处理,帧长取10 ms,即每帧441个采样点。 用MATLAB编程实现已知训练序列的LBG算法来产生码书。训练序列的长度为4 410 000个点,具体为100秒的男女声混合语音,分成10 000帧,每帧进行M=196的高斯随机观测,根据所得的观测值来训练生成码书。 实验一: 研究语音信号中的浊音帧、清音帧和过度帧的重构质量与观测数目M的关系。测试中的各语音帧取自不在训练集合中的女声 “二十万纳米”。如前所述,M的取值应满足公式M≥cKlog(N/K),实验中取下限,即令M=cKlog(N/K),已知N=441,又随机对多帧语音信号进行DCT变换后取K=50,现对常数c取不同的值,计算结果四舍五入至整数,得出M的值,进行高斯随机观测。然后对观测值进行矢量量化编码和矢量量化解码,通过OMP重构出语音信号。图4、图5和图6分别显示了c取不同值时浊音帧、清音帧和过度帧原信号与重构信号的波形对比。 图4 浊音帧在c取不同值时重构信号与原信号的时域波形对比Fig.4 The waveform comparison between the reconstructed signal and the original signal when c is different in voiced frame 可以看出浊音帧和过度帧c越大语音信号重构质量越高,而清音帧的重构效果与c的取值关系不大,且难以准确重构。这是因为清音近似高斯白噪声的原因。不过我们可以看出,虽然清音帧的重构信号波形不能准确的和原信号的波形重合,但是两者的包络却相差不大。又因为清音信号在语音信号中的能量占比很小,只有10%左右,对整个语音的重构影响不大。因此我们可以得出结论,在保证能重构语音信号的前提下,语音信号的重构质量与观测数目M正相关。 图5 清音帧在c取不同值时重构信号与原信号的时域波形对比Fig.5 The waveform comparison between the reconstructed signal and the original signal when c is different in unvoiced frame 实验二 研究在该编码方案下一句话的重构质量和该方案较原语音编码的压缩程度。实验分别对一句男声语音和一句女声语音进行。先定义压缩比r,第i帧信号的分段信噪比SNRseg(i)和平均分段信噪比SNRaseg。 根据压缩比r的定义,r的值越大说明该编码方案的压缩能力越强。 重构语音质量的客观评价采用平均分段信噪比SNRaseg,主观评价采用MOS分,MOS分采用ITU P.862标准算出。对不在训练集合中的两个语句进行处理,这两句语音的内容相同,时间长短相同,只是一句为男声一句为女声。实验结果如表1和表2所示。 图6 过渡帧在c取不同值时重构信号与原信号的时域波形对比Fig.6 The waveform comparison between the reconstructed signal and the original signal when c is different in intermediate frame 单独从是表1或表2的数据来看,平均分段信噪比SNRaseg和MOS值都与观测数目M正相关,这都进一步佐证了实验一的结论,即语音信号的重构质量与观测数目M正相关。对比两个表可以看出,在相同条件下,男声的重构质量较女声的重构质量好一些。这是因为女声中的细节更多,稀疏性较差一些的原因。在这个实验中还得出了压缩比r的数据,从中可以看出该编码方案具有很好的压缩性,在将原信号编码压缩6倍以上仍具有较高的重构质量。 表1 男声语音的重构质量和压缩比Tab.1 Reconstruction quality and compression ratio of male voice 实验可以看出该编码方案对CD音质的单声道语音信号压缩6倍以上仍具有较好的音质。虽然双声道的CD音质的语音信号压缩后的码速率仍需200 kbps左右,高于mp3标准的128 kbps,但mp3标准丢弃了大量人耳听不到的频段上的数据,而该方案实现了无损压缩。 表2 女声语音的重构质量和压缩比Tab.2 Reconstruction quality and compression ratio of female voice 文中对压缩感知应用于语音编码进行了研究,又运用了矢量矢量量化技术进一步降低了码速率。研究表明语音的重构质量与观测数目正相关,由此也可以看出观测矩阵在压缩感知中对信号重构的重要性,未来可以在自适应观测矩阵设计上进行研究,还可以研究应用熵编码进一步降低码速率以及压缩感知应用于语音编码的抗噪性。 [1]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [2]Cand s E,Tao T.Near-optimal signal recovery from random projections:Universal encoding strategies[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425. [3]Donoho D,Y Tsaig.Extensions of compressed sensing[J]. Signal Processing,2006,86(3):533-548. [4]石光明.压缩感知理论及其研究进展[J].电子学报,2009,37 (5):1070-1081. [5]范虹,郭鹏,王芳梅.非平稳信号稀疏表示的研究发展[J].计算机应用,2012,32(1):272-278. [6]Baraniuk R.A lecture on compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121. [7]E Cande s,Tao T.Decoding by linear programming[J].IEEE Transaction on information theory,2005,51(12):4203-4215. [8]Ji S,Xue Y,Carin L.Bayesian compressive sensing[J].IEEE Transactions on Signal Processing,2008,56(6):2346-2356. [9]张明君,高有行.利用改进K填充算法消除椒盐噪声[J].电子科技,2004(1):39-42. New speech coding scheme based on compressed sensing XU Jia-jia According to the sparse of the speech signal,applied compression perception theory to speech signal processing,this paper proposes a new scheme of speech signal coding.The method using random Gaussian matrix observing the speech signal on the encoding side,obtained fewer observations,then further compress the data using vector quantization coding.In the decoder,decoding by vector quantization,getting observations based on the speech signal sparsity in the discrete cosine domain,then reconstructed speech signal using orthogonal matching pursuit algorithm.The purpose of the algorithm is to reduce the computational complexity and delay on the premise of guarantee the quality of speech signal reconstruction. Experimental results show that the mono audio signal whose sampling rate is 44100 hz,quantitative is 16 bit and bit rate is 705.6 Kbps could be compressed to around 100 Kbps,the compressed speech signal still has good voice quality,at the same time the algorithm has lower time delay. compressed sensing;DCT;vector quantization;OMP TN912.3 A 1674-6236(2016)03-0032-05 2015-03-10稿件编号:201503139 许佳佳(1989—),男,江苏徐州人,硕士研究生。研究方向:信号处理。
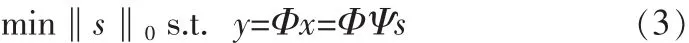
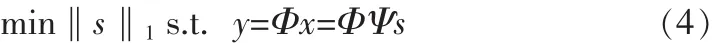
2 语音信号的稀疏性
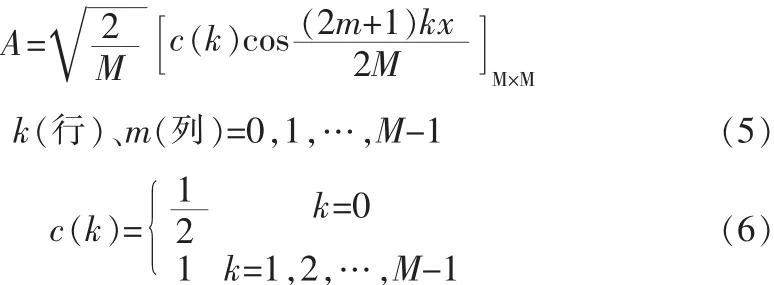
3 编码方案


4 仿真实验




5 结束语
(School of Computer Science,Shaanxi Normal University,Xi’an 710119,China)

