非均匀气隙永磁同步电机的有限时间自适应混沌同步

高振阳，王露露，施汀瑞

（河海大学 能源与电气学院，江苏 南京　210098）

非均匀气隙永磁同步电机的有限时间自适应混沌同步

高振阳，王露露，施汀瑞

（河海大学 能源与电气学院，江苏 南京210098）

以非均匀气隙永磁同步电机（PMSM）混沌系统为对象，提出一种有限时间自适应混沌同步控制方法。利用主动控制来实现动态误差系统非线性项和线性项的近似解耦，然后通过有限时间稳定理论和自适应控制技术来实现驱动-响应系统的混沌同步。通过仿真，验证本文所提控制策略的正确性和有效性。

永磁同步电机；有限时间稳定；自适应控制；混沌同步

自20世纪90年代Pecora和Carroll［1］首次提出具有不同初始条件的两个同类混沌系统的同步控制方法以来，混沌同步引起了广泛学者的关注。所谓混沌同步，就是对混沌系统施加控制，使该系统的轨道与另一混沌系统的轨道渐进的趋近一致。而混沌现象广泛存在于永磁同步电机、感应电机、直流电机开关磁阻电机等伺服系统中。其中，永磁同步电机（PMSM）具有体积小、重量轻、反应快、效率高等优点，随着电力电子技术和控制技术的发展，永磁同步电机交流伺服系统已经在现代高性能伺服系统中得到了极为广泛的应用［2］。1994年，Hematin［3］首次发现了永磁电机开环系统的混沌现象。PMSM混沌系统作为一种复杂的多变量、强耦合高维非线性系统，其混沌特性主要表现为：随着电机参数的变化，系统将呈现出转速或转矩的剧烈振荡、控制性能不稳定及系统不规则的电磁噪声等混沌现象，这将严重影响系统的动态性能。

目前关于PMSM混沌同步控制策略的研究还较少，文献［4］提出了利用线性状态反馈控制方法对PMSM的混沌运动进行控制；文献［5］基于Laypunov稳定性理论，设计了自适应控制器来进行控制；文献［6］基于滑模变结构控制理论，设计了一种具有强鲁棒性的自适应控制器来实现同步控制；文献［7］基于模糊控制理论，提出了模糊自适应同步控制方法实现了PMSM混沌运动的同步。这些控制器在一定程度上强调了系统的鲁棒性，但是没有从时间最优的角度来考虑系统的性能。近年来，有关混沌系统的有限时间稳定控制与同步的研究得到了广泛学者的关注［8-10］。而关于永磁同步电机（PMSM）的有限时间自适应混沌同步的研究还不多。

本文在文献［11］的基础上引入自适应控制，提出一种PMSM的新型的混沌同步控制器。基于主动控制和有限时间稳定控制，通过引入自适应的终端吸引子权系数，来进一步提高系统的快速响应能力。

1　系统描述

不失一般性，本文采用文献［11］所考虑的非均匀气隙PMSM模型:

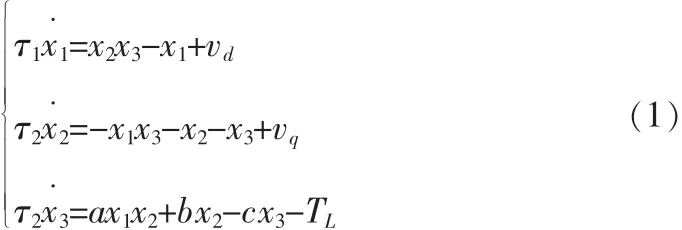
其中：（x1，x2，x3）=（id，iq，ω），vd，vq和id，iq分别为变换后d，q轴的等效电压和电流；ω和TL分别为变换后的等效速度和负载；a，b，c，τ1，τ2，τ3为相应变换后的模型参数，其具体的变换关系为：

其对应电机中具体参数的含义详见文献［5］，除时间t外其余各量均为无量纲的纯数，这里不再累述。由文献［5］分析可知：当满足下列参数时，PMSM将呈现典型的混沌现象。图1为非均匀气隙PMSM系统的三维相图。

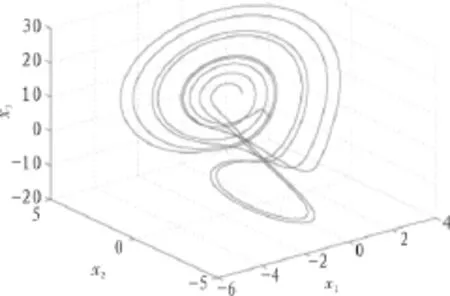
图1　永磁同步电机的相图Fig.1　The phase diagram of the PMWM

定义［11］：对于动态系统：=f（x），如果存在某一时刻T＞0（T可能与初始状态的选择有关），使得下面两个条件同时成立恒成立，则该系统是有限时间稳定的。其中x∈Rn为n维的状态变量，f（x）为光滑的非线性函数。定理1［11］：对于动态系统：=f（x），若存在一个连续函数V：U→R和一个正定函数r：R→R+使得下面的条件成立：①V正定；②（x，t）≤-r（V（x，t）），∀（x，t）∈U×I③存在实数ε＞0使得

则系统是有限时间稳定的，如果V是渐减的函数，则是一致有限时间稳定且稳定时间函数为其中时刻t*使得V（x（t*），t*）∈［0，ε］，则稳定所需的时间T=T（x0，t0）+t0，如果V是递减函数，则系统是一致有限时间稳定。

2　主要结论

设系统（1）为驱动系统，响应系统如下：

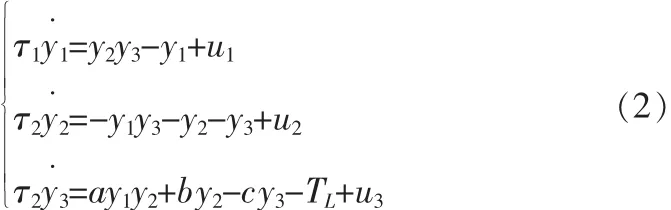
令ei=yi-xi，i=1，2，3则误差系统可表示为如下：

针对误差系统（3），基于主动控制，自适应控制以及有限时间稳定理论，设计的控制器如下所述。

定理2：对于误差系统（3），如果采用如下形式的控制器：

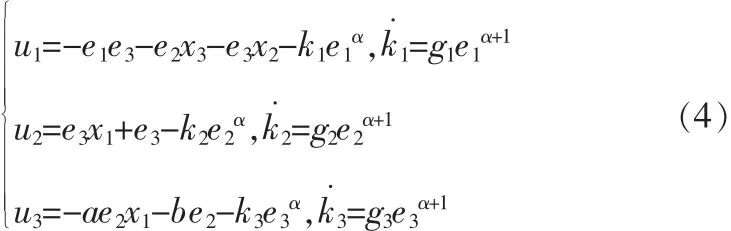
其中：g1，g2，g3均为正实数，为简化计算，取且p，q均为奇数，则系统（3）的状态误差在有限时间趋近于零。

证明如下：

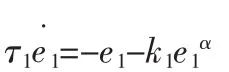
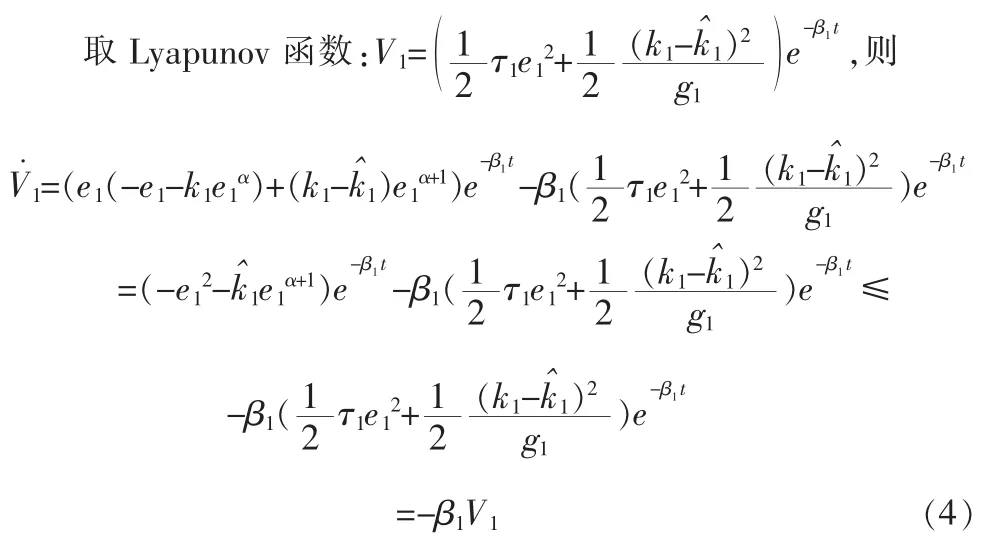
因此，当t≥t1时，将e1=0和u1，u2代入误差系统（3）的余下方程可得：

3　仿真分析

本部分主要是通过仿真与文献［11］（主动有限时间同步控制器）方案进行比较，验证本文方案的优越性。仿真采用四阶Runge-Kutta法，采样时间=0.01 s，初始条件（x1，x2，x3，y1，y2，y3）=（1，1，1，5，5，5），其余参数见第2部分。文献［11］的控制器为：

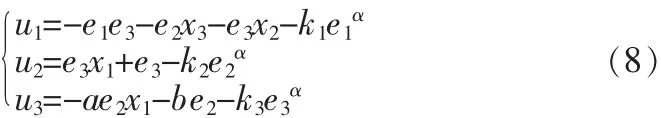
从形式可以看出，分数次幂对系统的响应能力的快慢影响较小，引入能够快速调整系统响应速度的可调参数。而本文中的可调终端吸引子权系数是自适应的，为了与文献［11］进行比较，本文控制器参数为仿真结果如下：

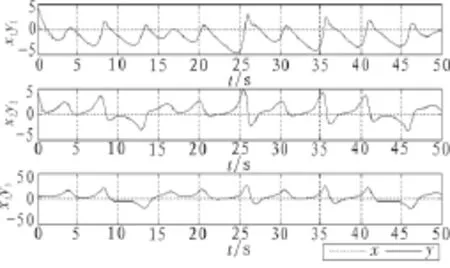
图2　文献［11］的方案Fig.2　The programme in the paper［11］

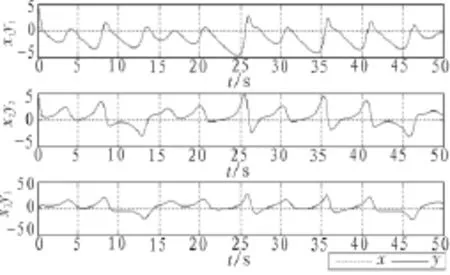
图3　本文的方案Fig.3　The programme in this paper

从图2、图3中可以看出，设计的有限时间自适应混沌同步控制器能够使系统较快的达到同步状态。

4　结　论

本文研究了PMSM［12］混沌系统的控制问题。通过主动控制与有限时间稳定理论和自适应控制相结合，该策略通过对终端吸引子比例系数进行自适应控制，有效地缩短系统的跟踪时间，来提高系统的响应能力。通过仿真，验证了本方案具有较好的性能，具有一定的研究价值。

［1］Pecora L M，Carroll T L．Synchronization in chaotic system ［J］．Phys，Rev，Lett．，1990，64（8）：821-824．

［2］李中华．有脉冲扰动的永磁同步电机混沌的直接力矩控制方法［J］．西南大学学报，2010，32（7）：139-145．

［3］Hemati N．Strange attractors in brushless DC motors［J］．IEEE Transactions on Circuits and Systems-Ⅰ：Fundamental Theory and Applications，1994，41（1）：40-45．

［4］韦笃取，罗晓曙．非均匀气隙永磁同步电机混沌的状态反馈控制［J］.广西师范大学学报，2006，24（1）：13-17．

［5］张兴华，丁守刚．非均匀气隙永磁同步电机的自适应混沌同步［J］．控制理论与应用，2009，26（6）：661-664．

［6］杨晓辉，刘小平，胡龙龙．永磁同步电机的鲁棒滑模变结构混沌同步控制［J］．组合机床与自动化加工技术，2012，8：93-95．

［7］王磊，李颖晖，朱喜华．存在扰动的永磁同步电机混沌运动模糊自适应同步［J］．电力系统保护与控制，2011，39（11）：33-37.

［8］丁世宏，李世华．有限时间控制问题综述［J］．控制与决策，2011，26（2）：161-169．

［9］Wang H，Han Z Z，Xie Q Y．Finite-time chaos synchronization of unified chaotic systems with uncertain parameters ［J］．Communication Nonlinear Science Number Simulation，2009，14：2239-2247．

［10］陈国培，杨莹，李俊民．非线性系统有限时间稳定的一个新的充分条件［J］．控制与决策，2011，26（6）：837-840．

［11］唐传胜，戴跃洪，甄文喜．非均匀气隙永磁同步电机的有限时间混沌同步［J］．控制理论与应用，2014，31（3）：404-408．

［12］朱卫云，付东翔，葛懂林.基于RBF神经网络的永磁同步伺服电机控制系统［J］.电子科技，2016（1）：161-164，168.

Finite-time adaptive chaos synchronization of permanent magnet synchronous motor with non-smooth air-gap

GAO Zhen-yang，WANG Lu-lu，SHI Ting-rui
（College of Energy and Electrical Engineering，Hohai University，Nanjing 210098，China）

A novel finite-time adaptive synchronization controller is proposed for the permanent magnet synchronous motor （PMSM）with non-smooth air-gap.In the proposed control strategy，the active control is used to decouple the linear terms and nonlinear terms of the dynamic error system.Then，based on the finite-time stability theory and adaptive control approach，the designed novel controller could realize chaos synchronization of the drive-response system in finite time.Finally，numerical simulations are provided to demonstrate the effectiveness and usefulness of the proposed finite-time adaptive control strategy.

permanent magnet synchronous motor（PMSM）；finite-time stability；adaptive control；chaos synchronization

TN713

A

1674－6236（2016）05-0097-03

2015-04-13稿件编号：201504132

高振阳（1991—），男，江苏南京人，硕士研究生。研究方向：分数阶卡尔曼滤波理论及其应用、电力系统的参数辨识等。