基于改进遗传算法的钣金折弯自动工序规划*

柳守宽　郑联语　杜瑞芳　陈光进

(①北京航空航天大学机械工程与自动化学院，北京 100191；②北京航天数控系统有限公司，北京 100080)



基于改进遗传算法的钣金折弯自动工序规划*

柳守宽①郑联语①杜瑞芳②陈光进②

(①北京航空航天大学机械工程与自动化学院，北京 100191；②北京航天数控系统有限公司，北京 100080)

为了提高钣金折弯工序规划的效率，需要保证在不干涉的前提下，为每个工步选择合适模具，使得模具更换、板料的掉头和翻转次数尽可能少。为此，采用一种改进的高效遗传算法对折弯工序进行优化设计。该方法将发生干涉的工序位置引入适值的计算，在初始种群中快速进化出更优个体，同时为了提高遗传算法的收敛速度，将每一代中的最优个体直接保存到下一代中。实验结果表明该算法相对传统方法更具有高效性，能够快速得到近似最优解的工序方案。

折弯；遗传算法；工序规划

由于钣金折弯零件具有强度高、质量轻、成本低、加工简单和生产效率高等优点，其在机械、通信、电子电器等领域内得到了越来越广泛的应用。钣金零件的加工过程中，折弯的顺序严重影响加工效率和零件精度。传统的折弯工序规划需要设计人员人工规划，且需相当长的试验和调整时间，工序方案的可行性也很难进行判断，因此效率低且可靠性不高。快速、高效、可靠地自动工序规划是钣金件折弯中一个亟需解决的问题。

国内外对折弯工序优化的方法与理论进行了广泛深入的研究。M.Inui等以零件的拓扑结构作为约束条件，过滤掉不合适的折弯工序，提高了规划效率[1]。Duflou J提出一种基于优先约束方法和分支界线法解决旅行商问题[2]。J.C.RICO，J.M.GONZALEZ等提出一种解决折弯工序规划的方法，它将折弯件划分为一些基本的形状单元，然后分别局部对其进行工序规划，最后将这些子单元的工序组合成完整的折弯工序[3]。Thanapandi C.M等提出了一种工序规划预处理的遗传算法来减少搜索空间[4]。Duflou J等对折弯排序做了一个详细的综述[5]。Kannan T R等提出了一种遗传算法得到接近最优解的折弯工序[6]。M.A.Farsi等在折弯规划过程中引入了分类系统和模糊集理论[7]。王飞等人开发一种独立于零件特征的折弯工序自动规划系统，采用遗传算法，在交叉和变异过程中引进约束条件以缩短迭代计算的时间[8]。但是上述工序规划算法的研究中，对于发生干涉的工序，其优劣情况未做考虑，导致较难进化出不干涉的工序，其次算法的收敛曲线有一定的波动，使得收敛时间加长。

基于以上问题，本文采用一种改进的遗传算法来规划钣金折弯的工序，从而保证折弯工序规划的合理性和高效性。

1　折弯工序规划遗传算法的改进

折弯工序规划是由多个工步组成的工序评估过程，利用遗传算法对折弯工序进行规划时，需要为工序评估选择合适的适应函数，其次选定一组初始种群，经过复制、交叉和变异操作进化出更优的个体。本文遗传算法的改进主要从适应函数、初始种群和进化过程3方面改进。

1.1适应函数选取

F=∑wiNi

(1)

式中：F表示适值；Ni分别代表模具总数N1、模具拆卸次数(模具更换和改变方向)N2、板料翻转次数N3、板料掉头次数N4和操作不平衡次数N5;Wi表示相应各因素的权值。权值分别取w1=100、w2=50、w3=15、w4=10、w5=5，其中操作不平衡是指加工过程工人抓取工件时，折弯线到后挡料的距离大于到工人的距离。适值越小，说明这种折弯工序方案越优。

但对于发生干涉的折弯工序，其也有优劣之分，此外干涉的折弯工序属于不可行的方案，适值一定要比无干涉时大。为了在遗传算法中能够快速地进化出无干涉的折弯工序，本文定义其干涉时的适应函数为：

F=∑wiN+(N-p)max(wi)

(2)

式中：N表示工件总折弯数；p(p∑wiNi，故∑wiN能确保发生干涉的工序适值大于不干涉时的适值，(N-p)max(wi)是根据发生干涉的位置定义干涉工序的优劣。

1.2初始种群优化

对于折弯数较多、结构较为复杂的钣金件，在初始种群的选定时随机性太强，适值普遍偏大，使得在后代进化过程中收敛速度较缓慢。为此本文在产生初始种群后，将种群中的最优个体经过相应的优化操作来获得适值更小的个体。

以图 1所示的折弯工序(3,4,6,9,8,2,1,5,7)为例，对每个工步依次进行干涉检测，对于发生干涉的工步，则将其依次与后面的折弯号对换并重新检测干涉情况。若某工步无论怎么对换都发生干涉，此时停止检测过程，虽然没有获得不干涉个体，但至少可以获得一个相对较优的个体。

1.3进化过程改进

进化过程需进行复制、交叉和变异操作不断产生新的种群。本文复制操作采用转轮法，并取适值的倒数来计算，交叉采用部分匹配交叉操作(PMX)，设置交叉概率为0.9，变异采用对换操作，设置变异概率为0.1。

依据《现代汉语词典》的解释，公信力即是公众信任的力量。公信力是指在社会生活中，公共权力面对时间差序、公共交往以及利益交换表现出的一种公平、正义、效率、民主、人道、责任的信任力。地方政府官员微博的公信力可以理解为地方政府官员微博具有的使公众信任的力量。官员微博公信力的影响因素主要包括信息的真实、全面、及时，内容的思想高度，官员个人的素质修养等方面。官员微博的公信力对其发展和作用的有效实现具有重要的意义。

由于在进化过程中，经过交叉操作后下一代的解很可能不会出现更优的解，而导致丢失当前最优解，使得收敛速度变慢，因此可将每一代中最优解直接保存到下一代中。同时为了避免出现局部最优解，将该最优解强制进行变异操作，即变异概率为1，若变异后更优则直接保存到下一代中，反之仍然保存原当前最优解。此过程可使每一代种群都朝着更优的方向进化。

2　折弯工序自动规划过程

折弯工序规划需要在综合考虑干涉碰撞、折弯效率和操作平衡性等因素的前提下，为每个工步选择一个合适的模具，使得适值尽可能小。

2.1模具自动选择

模具包括上模和下模，选择何种模具是由工件的特征参数决定的，在选择模具时既要保证模具和板料之间不发生干涉，同时还要尽可能保证折弯后的工件与实际要求符合。

首先根据工件的折弯特征指定的折弯角、折弯半径和板料厚度，初步为每个工步筛选出符合条件的所有模具。

然后在工序评估过程中根据优先级对模具进行再一次筛选。优先级最主要有两个方面：第一尽量避免使用特殊模具，优先选择标准模具；第二钣金折弯中模具的角度一般选择比折弯角略小，角度越接近折弯角的模具优先级越高，对于每一道折弯需要保证上模和下模的角度相同。

2.2折弯工序自动规划

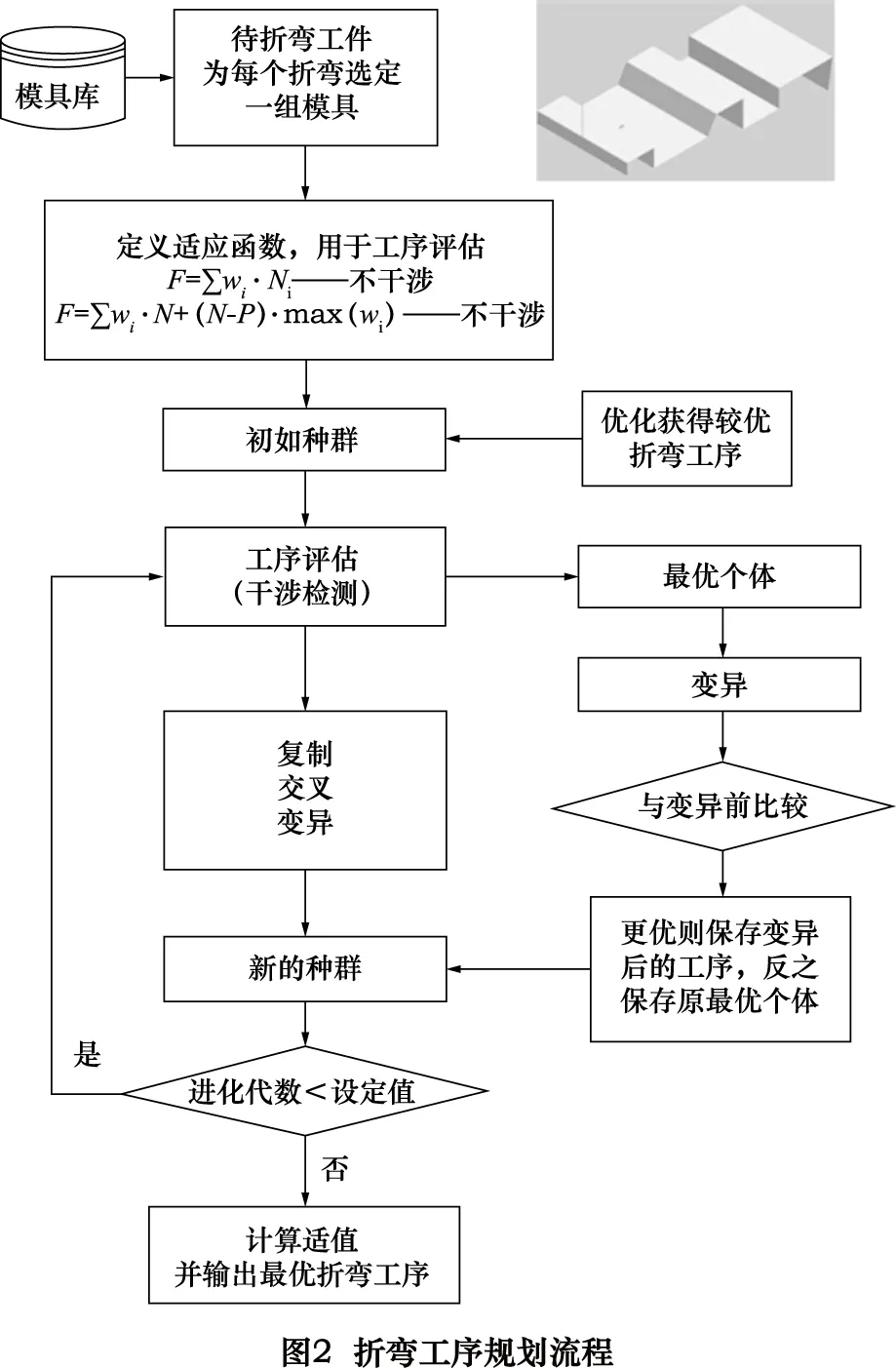
利用上述改进的遗传算法规划折弯工序的具体流程如图2所示。

(1)工序规划前处理 从模具库中为每个折弯选定一组模具，定义适值函数和初始种群。

(2)工序评估主要是计算适值大小。适值是遗传算法种群进化的重要依据，决定了个体是否被淘汰或复制，同时也是评定工序优劣的唯一指标。

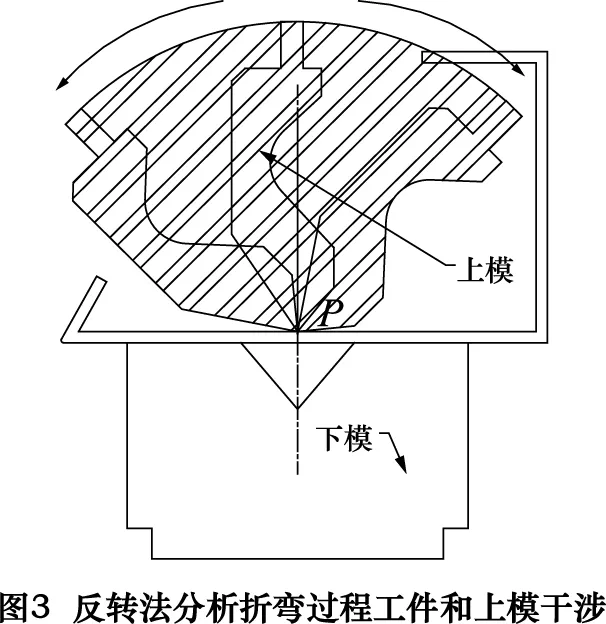
在计算适值的过程中应尽可能保证每个工步的折弯过程不发生干涉。干涉需要分别检测工件与机床、模具、后挡料之间的干涉。如图3所示，以上模为例，采用反转法将上模分别逆时针和顺时针绕与工件接触P点旋转折弯角的一半，围成图示的阴影部分区域，若工件与阴影部分有交集则表示发生干涉。

此外当工件有尺寸精度要求时，后挡料定位点的选择必须考虑工件的精度要求，使得尺寸偏差累积在精度要求低的折弯段上。

(3)种群进化 对每一代中最优个体直接进行强制变异操作，将其与变异前适值比较后保存更优个体到下一代种群中。而对于非当前最优个体，直接进行复制、交叉和变异操作产生下一代种群。经过若干代后便能进化出相对更优的折弯工序。

3　实例验证及应用

以图4所示钣金件为例来验证本遗传算法的有效性，其中工件壁厚为2 mm，折弯半径均为2 mm，宽度为400 mm。

根据工件的特征参数自动从库中选择符合条件的模具，然后按其角度大小设置其优先顺序，图5所示为该工件可选的所有模具，分别给各模具标号。其中4号上模和3号下模角度大于90°，只适用于钣金件中120°的4、5号折弯。

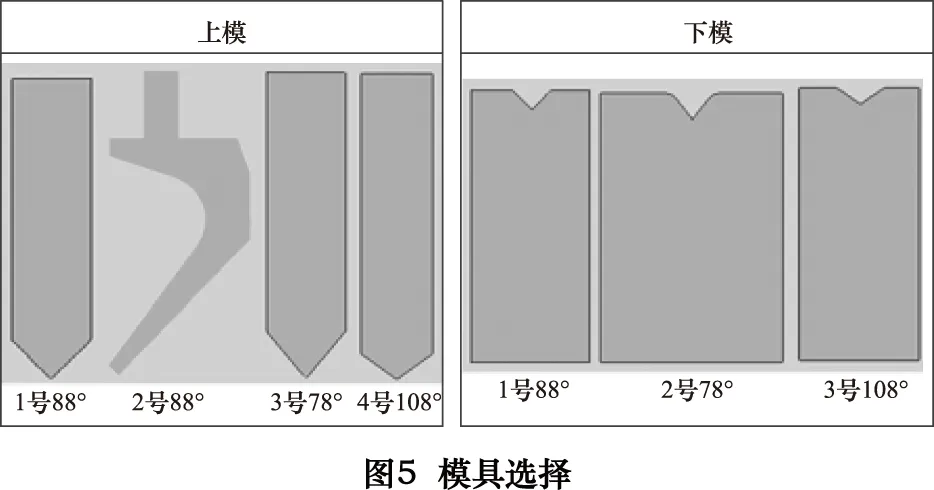
表1遗传算法优化结果

折弯工序方案上模下模N1 N2 N3 N4 N5适值F-3,8,6,1,9,7,2,10,-4,-51,1,1,1,1,1,2,3,4,21,1,1,1,1,1,1,2,3,14 7 2 5 1835-3,8,6,9,7,1,2,10,-4,-51,1,1,1,1,1,2,3,4,21,1,1,1,1,1,1,2,3,14 7 2 5 1835-3,8,6,9,1,7,2,-4,10,-51,1,1,1,1,1,2,4,3,21,1,1,1,1,1,1,3,2,14 7 4 5 1865-1,8,-3,6,10,2,9,4,7,-51,1,1,1,3,2,1,4,1,21,1,1,1,2,1,1,3,1,14 10 4 4 010003,1,9,2,8,10,6,4,5,71,1,1,2,1,3,-,-,-,-1,1,1,1,1,2,-,-,-,-- - - - -2100

定义初始种群大小为20，演化代数为100，设置工件和模具的默认正方向，利用上文的优化遗传算法规划工序，将最终结果按适值大小排列并取5个方案，如表 1所示。

对于不干涉的工序方案，表中折弯工序中的负号表示工件的方向与默认方向相反，干涉时不定义工件方向。表中最后一个工序方案在第7个工步发生干涉时，该工位找不到合适的模具。

整个遗传算法过程中适值变化如图 6所示，在第一代时最优解的适值为895，没有发生干涉，说明初始种群的优化过程中出现了不干涉的个体，使得整个遗传算法收敛速度更快。本折弯件在第21代时就可以到达近似最优解，共使用2.7 s的时间。

在初始种群优化过程中也有可能无法出现可行的折弯解，如图 7所示，在第一代时最优解的适值为1 800，虽然发生干涉，但其收敛速度同样非常快，在第29代就到达近似最优解，用时3.8 s左右。

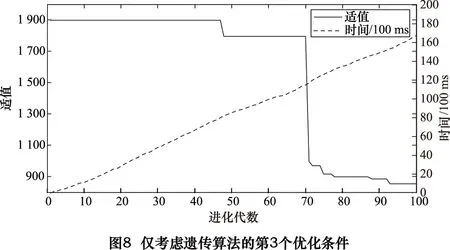
若不采用本文遗传算法的前两个改进条件，即不考虑干涉时的适应函数以及初始种群的优化，仅改进进化过程来保存当前最优解，其结果如图 8所示。到第70代以后才出现不干涉的折弯工序，达到近似最优解的时间将近16 s，其大部分时间浪费在进化出可行折弯解的过程中，此时需要设置更大的进化代数或种群大小。

此外若不考虑第3个改进条件保存当前最优解，适值曲线波动较大，经试验在100代内很有可能不出现可行的折弯工序。

开发一套工序规划及仿真软件，以第一种折弯工序方案(-3,8,6,1,9,7,2,10,-4,-5)为例，利用本软件展示其折弯过程，结果如图 9所示。

4　结语

利用改进的遗传算法对钣金工件进行工序规划，将干涉位置引入发生干涉时的适应函数，确保能快速进化出可行的不干涉工序；优化初始种群获得相对更优的个体，使得遗传算法的进化起点更优；保存当前最优解到下一代，以确保不丢失当前最优解，使得种群朝着越来越优的方向进化。结果对比后验证了该算法的有效性，能快速得到近似最优解，并避免出现局部最优解。

[1]Inui M, Terakado H. Fast bending sequence planning for progressive press-working[C].Assembly and Task Planning, 1999.(ISATP'99)Proceedings of the 1999 IEEE International Symposium on. IEEE, 1999: 344-349.

[2]Duflou J, Kruth J P, Van Oudheusden D. Algorithms for the design verification and automatic process planning for bent sheet metal parts[J]. CIRP Annals-Manufacturing Technology , 1999, 48(1): 405-408.

[3]Carlos Rico.J M González,S Meteos,et al.Automatic determination of bending sequences for sheet metal parts with parallel bends[J]. International Journal of Production Research，2003，41(14): 3273-3299.

[4]Thanapandi C M, Walairacht A, Periasamy T, et al. Preprocessor to im prove performance of GA in determining bending process for sheet metal industry：foundations of intelligent systems [M]. Springer Berlin Heidelberg, 2002: 362-373.

[5]Joost R Duflou, Jozsef Vancza, Richard Aerens. Computer aided process planning for sheet metal bending:a state of the art[J]. Computers in Industry, 2005, 56(7): 747-771.

[6]Kannan T R, Shunmugam M S. Planner for sheet metal components to obtain optimal bend sequence using a genetic algorithm[J]. International Journal of Computer Integrated Manufacturing, 2008, 21(7): 790-802.

[7]Farsi M A, Arezoo B. Development of a new method to determine bending sequence in progressive dies[J]. The International Journal of Advanced Manufacturing Technology, 2009, 43( 1-2): 52-60.

[8]王飞, 游有鹏. 基于遗传算法的板金自由折弯工序的优化设计[J]. 机械科学与技术, 2011, 30(6): 991-995.

(编辑汪艺)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Automatic procedure planning based on an improved genetic algorithm for sheet metal bending

LIU Shoukuan①, ZHENG Lianyu①, DU Ruifang②, CHEN Guangjin②

(①Mechanical Engineering and Automation Department, Beihang University, Beijing 100191,CHN; ②Beijing Aerospace Numerical Control System Co.,Ltd., Beijing 100080, CHN)

In order to ensure the efficiency of process planning, it needs to choose the appropriate tools for each step to make the number of tool, tool changes, part turn around and flip-overs minimal on the premise of non-interference. In this paper, an improved efficient genetic algorithm is developed to optimize the design of the bending procedure planning, which introduces the step position of interference to calculate the fitness and evolves the better individual in the initial population. Meanwhile, for the sake of improving the convergence rate, this algorithm saves the best solution of current generation to next generation. The results show that the algorithm is highly efficient and can quickly obtain the approximate optimal sequences.

bending; genetic algorithm; process planning

中图文分类号：TH164B

10.19287/j.cnki.1005-2402.2016.06.017

柳守宽，男，1991年生，硕士，研究方向为数字化设计与制造、钣金折弯工艺。

2015-11-17)

160633

* 高档数控机床与基础制造装备国家科技重大专项(2014ZX04009011)