PCNN赋时矩阵高斯噪声滤除算法

张文兴，闫海鹏，王建国

（内蒙古科技大学机械工程学院，内蒙古　包头　014010）

PCNN赋时矩阵高斯噪声滤除算法

张文兴，闫海鹏，王建国

（内蒙古科技大学机械工程学院，内蒙古包头014010）

为消除图像降噪过程中传统降噪方法对图像边缘和细节的影响，提出一种基于改进脉冲耦合神经网络（pulse coupled neural network，PCNN）赋时矩阵的有效滤除高斯噪声算法。该算法将PCNN模型的突触联结强度改进为随神经元与其周围神经元相似程度不同而变化的可变值，并将PCNN神经元的点火时间记录在赋时矩阵中，根据点火时刻判断噪声点，选择滤波方式。实验结果表明：该算法能够有效去除高斯噪声，具有较强的降噪性能及很好的边缘与细节保护能力。

脉冲耦合神经网络；赋时矩阵；高斯噪声；突触联结强度；可变值

0　引言

图像在传输过程中，经常受到各种噪声的干扰，其中常见的有高斯噪声和脉冲噪声两种［1］。脉冲噪声属于极端噪声，容易定位和滤除，而高斯噪声服从高斯分布，图像被污染后其所有像素点均受到不同程度的污染，因此滤除很难。图像降噪效果的好坏直接影响着图像的后续处理，传统的均值、中值滤波及一些改进的滤波方法［2-4］，在对图像去除噪声后会损坏图像的一些边缘细节，使图像变得模糊，滤波效果不佳。

脉冲耦合神经网络［5-6］（pulse coupled neural network，PCNN）是1990年Eckhorn根据猫的大脑视觉皮层上同步脉冲发放现象提出的，它不同于传统的人工神经网络，属于第3代人工神经网络。它是由许多神经元相互连接形成的一种动态非线性神经网络，具有同步脉冲发放特性，能够比传统的人工神经网络更好地模拟生物学行为。近年来，PCNN已广泛应用于图像处理的各个领域［7-11］，尤其在图像高斯滤波处理中，PCNN更优于传统的滤波方法［12-15］。其中，文献［8］将PCNN模型、维纳滤波、均值滤波组合用于去除高斯噪声，该方法不仅能有效去除噪声，同时更好地保持了图像细节和边缘；文献［12］利用赋时矩阵定位噪声点进行分类滤波，并能自适应调整灰度补偿步长，可以有效去除噪声且较好保持图像的边缘细节；文献［14］利用PCNN的同步脉冲特性对图像小波系数进行局部加窗修正，且提出了自适应连接系数，在去噪方面有较高的峰值信噪比，较好的视觉效果。

为有效去除高斯噪声，同时保护图像的边缘和细节，本文根据高斯噪声的特点及PCNN同步脉冲发放特性，提出了一种PCNN可变突触联结强度赋时矩阵模型。

1　PCNN模型

1.1基本PCNN模型

一个PCNN神经元由接受域、调制域、脉冲产生部分3部分组成。其数学表达式用以下方程来描述。

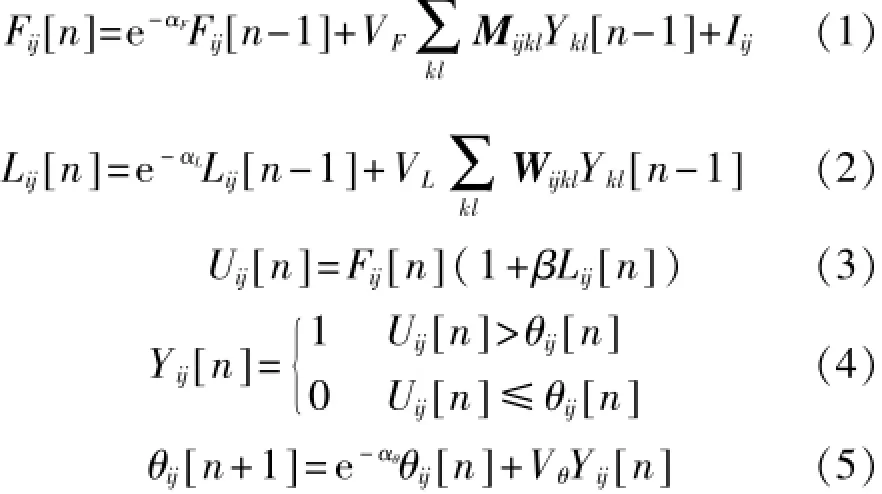
式中：Fij［n］——第（i，j）个神经元的第n次馈送输入；

Lij——外部激励；

Lij［n］——连接输入；

Mijkl，Wijkl——神经元（k，l）与（i，j）之间F通道与L通道的突触连接权系数矩阵；

Ykl——神经元（k，l）输出；

β——突触联结强度；

Uij［n］——内部状态信号；

θij［n］——动态阈值；

αF、αL、αθ——相应的衰减时间常数；

VF、VL、Vθ——相应的幅度系数；

Yij［n］——神经元（i，j）输出。

接受域接收来自其他神经元的反馈输入与外部输入，接收到的信号通过L和F两条通道传输；调制域将Lij与突出联结强度β相乘后作常数1的偏移，再与Fij相乘调制得到内部状态信号Uij；脉冲产生部分由阈值调节器、比较器与脉冲产生器组成，将内部状态信号Uij与动态阈值θij进行比较来控制神经元的点火输出Yij。

1.2简化PCNN模型

由于基本PCNN模型在应用时可控参数较多，不易调节，因此在保证原有PCNN模型特性的同时常将其模型进行简化。本文将式（1）、式（2）简化为式（6）、式（7）。

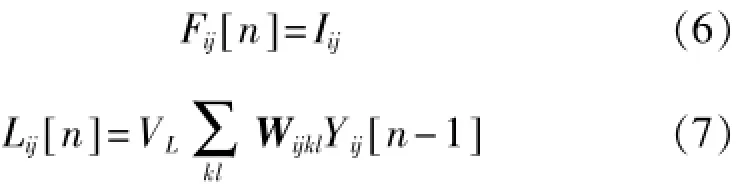
由上式可以看出，简化后的PCNN模型外部输入仅与图像像素点的灰度值有关，而连接输入去掉了指数衰减部分，因此简化后的PCNN模型减少了参数设置的同时，在一定程度上保持了原有模型的特性：状态相似的神经元依然能够同步发放脉冲；内部状态信号的组成方式没有改变，并且连接输入作用的大小仍由突触联结强度决定。简化后的PCNN神经元模型如图1所示。

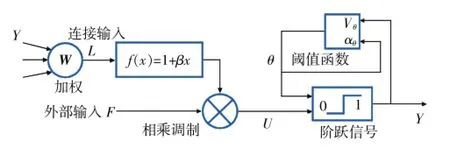
图1　 简化PCNN神经元模型

2　PCNN可变突触联结强度赋时矩阵高斯滤波算法

2.1可变突触联结强度

突触联结强度决定着神经元内部状态信号中连接输入所占的权重。其值越大，表明该神经元周围的神经元对其影响越大，越容易受到周围已点火神经元的捕获而提前点火发放脉冲，其值越小则相反。一般应用PCNN模型对图像处理时常将突触联结强度设定为某一定值，本文将突触联结强度改进为可变值如式（8）、式（9）所示。

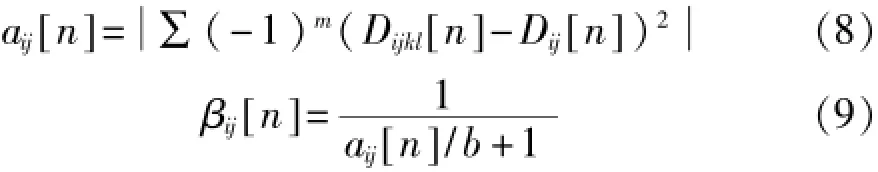
其中Dijkl为神经元（i，j）3×3邻域内（k，l）神经元所对应的像素灰度值，Dij为神经元（i，j）对应的像素灰度值，m为正整数，当Dijkl［n］-Dij［n］为正时，令m=1，否则令m=2，b是Dijkl的个数。

当一个神经元点火时，会影响周围其他相似神经元激活点火，使灰度值相近的神经元同时点火发放脉冲，而βij值越大，其神经元周围其他神经元越容易发生点火，即越相似的神经元，越容易被已点火的神经元捕获而提前激活点火，形成同步发放出脉冲的现象，即PCNN的捕获和同步脉冲发放特性。根据高斯噪声的特点及PCNN同步脉冲发放特性，本文将神经元（i，j）的突触联结强度βij改进为随其与周围神经元相似程度的不同而变化的可变值，如式（8）、式（9）所示。其中aij的取值为神经元（i，j）邻域内每个神经元与该神经元差值的平方（如果差值为正，平方之后取负值）再求和。aij值越小表明神经元（i，j）与周围神经元的相似程度越高，βij取值就越大，该神经元被捕获提前点火的几率就大，否则相反。

2.2PCNN赋时矩阵

PCNN赋时矩阵记录了每个神经元的初次点火时刻，反映了基于图像空间信息的时间域信息，体现了图像空间结构到时间序列的映射，其数学表达式为

其中n为点火时刻，赋时矩阵T大小与外部输入I及输出Y相等且它们的元素一一对应，Tij记录神经元（i，j）的初次点火时间，其赋值循环过程为：如果神经元（i，j）从未点火，则Tij为0；如果神经元（i，j）在第n时刻首次点火，则Tij为n；如果神经元（i，j）已经点过火，则Tij保持不变。直到所有神经元都点火，即T中每个元素都不为0时，停止迭代。

在赋时矩阵T中，若元素Tij的（2k+1）×（2k+1）邻域内有一半以上元素值与Tij不相等，则认为元素Tij所对应的像素点是噪声点，否则不认为其为噪声点。

2.3算法过程

1）初始化神经网络：设置各个参数，输入待处理图像I，同时令每个像素对应的神经元均处于熄火状态，即Yij=0。

2）含噪图像的预处理：给定较小值Δθ，在I中将满足条件Iij＜Δθ的像素点灰度值用Δθ代替，将满足条件Iij＞G-Δθ的像素点灰度值用G-Δθ代替，其它像素点灰度值不做处理，这样生成待处理图像I′，其中G为灰度级。

3）生成赋时矩阵T：对待处理图像I′根据式（3）～式（10）进行迭代循环，直到所有像素点都点火为止。当在第n次循环中，某一神经元（i，j）初次点火，即其输出Yij=1，点火时刻矩阵中该神经元对应点元素Tij［n］=n；若其重复点火，则Tij［n］的值保持初次点火时的值不变（可令初次点火时刻后该神经元的阈值为一较大值，从而避免其重复点火）；当在第n次循环中，某一神经元（i，j）未点火，即Yij=0，则Tij［n］= Tij［n-1］。

4）判断迭代是否停止：若T中所有元素均不为0，则停止迭代，转到5）判断噪声点，否则转到3）继续循环迭代。

5）判断噪声点：若矩阵T中元素Tij的3×3邻域内有一半以上元素值与Tij不相等，则认为I′ij是噪声点，其他情况不认为I′ij是噪声点。

6）选择滤波方式：根据5）中对噪声点的判定，依据以下策略自适应选择相应的滤波方式：

a）如果I′ij是噪声点，且Tij在其3×3邻域内最大或最小，对I′ij采用中值滤波。

b）如果I′ij是噪声点，且除a）步骤情况，则对I′ij采用维纳滤波。

c）如果I′ij不是噪声点，且Tij在其3×3邻域内的所有元素值均相等，则直接输出I′ij。

d）其他情况采用均值滤波进行降噪。

7）最后对全部像素点做维纳滤波。

3　实验结果分析

为了测试本文算法对图像降噪的效果，以大小为256×256的Lena图像为例，分别添加均值均为0，方差不同的高斯噪声对本文算法进行测试，并与均值滤波、中值滤波、文献［12］及文献［13］方法进行降噪效果比较。测试中的参数选择为：VL=0.7、αθ=0.2、Vθ=5、W=［0.5 1 0.5；1 0 1；0.5 1 0.5］、Δθ=10、θ0=260，滤波窗口均为3×3。滤波结果采用峰值信噪比PSNR和信噪比改善因子R两项指标客观评价，其单位均为dB。

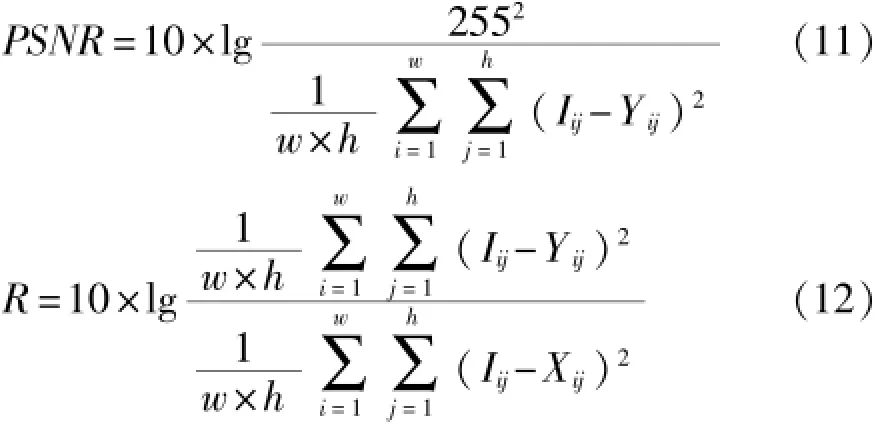
其中：w、h表示图像像素的行、列数，I表示原始图噪图像，X表示对噪声图像，Y表示对噪声图像处理后的图像。PSNR值越大，表明滤波效果越好；R为负值，则表明滤波后噪声被有效地抑制，且R值越小，滤波效果越好。

图2　Lena图像，均值为0、方差为0.008的含噪图像及各方法滤波后的图像

图2为原始Lena图像、添加均值为0、方差为0.008的高斯噪声图像及均值滤波、中值滤波、本文算法滤波后的图像。图3为原始Lena图像、添加均值为0、方差为0.02的高斯噪声图像及均值滤波、中值滤波、本文算法滤波后的图像。由图2和图3可以看出，本文算法降噪视觉效果要比中值滤波、均值滤波好得多，体现了本文算法去噪能力强的特点。

为了验证本文算法对图像边缘和细节保护能力，采用canny算子对图像边缘检测。图4为图3相应图像采用canny算子进行边缘检测后的图像，由图可以看出本文算法能够更好地保护图像边缘与细节。

表1为均值滤波、中值滤波、文献［12］方法滤波及本文算法滤波对Lena图像降噪后的PSNR性能比较。从表中能够看出，均值为0、方差为0.005～0.009时，本文算法的PSNR值最高，表明在表中的滤波方法中本文算法的滤波效果最好。

图3　Lena图像，均值为0、方差为0.02的含噪图像及各方法滤波后的图像

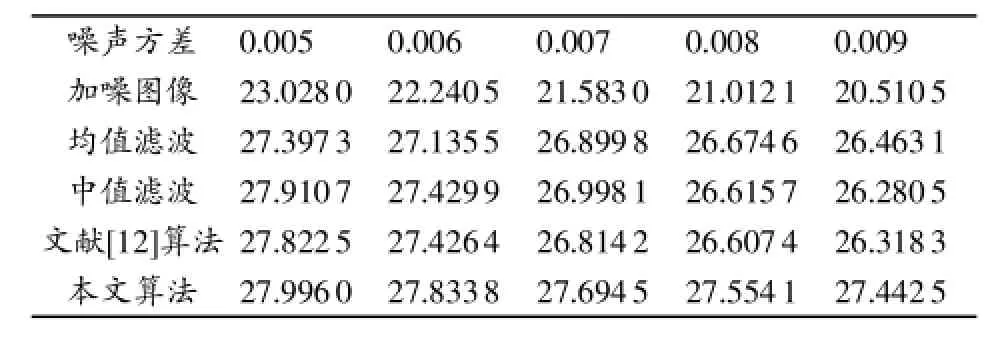
表1　Lena图像采用不同滤波方法时PSNR性能比较

表2　Lena图像采用不同滤波方法时信噪比改善因子R比较

图4　图3相应图像的canny算子边缘检测效果

表2为均值、中值、文献［13］方法及本文算法滤波对Lena图像降噪后信噪比改善因子R的比较。由表中的数据可以看出本文算法得到的R值比表中另外3种滤波方法的R值更小，表明滤波后图像对噪声的抑制程度更高，即本文算法的滤波效果更好。表1与表2中的数据除PSNR值和R值为相应文献中原始数据外，其他值均为多组测试结果平均值。

4　结束语

本文提出了一种简化PCNN可变突触联结强度赋时矩阵滤波算法：首先将PCNN模型简化，并将突触连接强度改进为可变值，使其取值与周围神经元的相似程度有关；其次将神经元初次点火时刻记录在赋时矩阵中，并依据赋时矩阵中元素的值定位噪声点；然后根据是否为噪声点选择滤波方式滤波；最后进一步对图像进行维纳滤波。实验结果表明，本文算法优于与之比较的其他方法，得到的降噪图像有更好的主观效果，客观评价指标更好于其他方法。因此本文算法能够有效地去除高斯噪声，具有较强的去噪能力，同时很好地保护了图像的边缘和细节。

［1］GARNETT R，HUEGERICH T，CHUI C，et al.A universal noise removal algorithm with an impulse detector［J］.IEEE Transactions on Image Processing，2005，4 （11）：1747-1754.

［2］朱士虎，游春霞.一种改进的均值滤波算法［J］.计算机应用与软件，2013，30（12）：97-99.

［3］赵高长，张磊，武风波.改进的中值滤波算法在图像去噪中的应用［J］.应用光学，2011，32（40：678-682.

［4］李旭，赵文杰，杨凯达.一种改进的中值滤波算法［J］.中国体视学与图像分析，2013，18（1）：7-11.

［5］JOHNSONJL，PADGETTM L.PCNN models and applications［J］.IEEE Transactions on Neural Networks，1999，10（3）：480-498.

［6］马义德，李康，王亚馥，等.脉冲耦合神经网络原理及其应用［M］.北京：科学出版社，2006：16-47.

［7］顾晓东，余道衡，郭仕德.关于PCNN应用于图像处理的研究［J］.电讯技术，2003（3）：21-24.

［8］刘莉，谈文蓉.一种基于PCNN的有效去除高斯噪声的方法［J］.西南民族大学学报（自然科学版），2012，38（4）：642-647.

［9］沈艳，张晓明，韩凯歌，等.PCNN图像分割技术研究［J］.现代电子技术，2014，37（2）：38-41.

［10］郭传奇，汪文革，储彬彬.一种改进的PCNN图像融合算法［J］.计算机工程与应用，2011，47（19）：176-178.

［11］李建锋，辛国江.一种基于PCNN的医学图像边缘提取方法［J］.计算机应用研究，2010，27（11）：4389-4393.

［12］程园园，李海燕，张榆锋，等.基于可变步长PCNN赋时矩阵高斯噪声滤波［J］.计算机工程与设计，2011，32（11）：3857-3860.

［13］高超，须文波，孙俊.新的强高斯噪声自适应滤波方法［J］.计算机工程与应用，2011，47（28）：154-157.

［14］宫霄霖，毛瑞全.结合PCNN和局部维纳滤波的图像去噪［J］.北京邮电大学学报，2011，34（5）：67-70.

［15］张红娟.基于PCNN的图像去噪和图像增强方法研究［D］.兰州：兰州大学，2011.

（编辑：刘杨）

Gaussian noise filtering algorithm based on PCNN time matrix

ZHANG Wenxing，YAN Haipeng，WANG Jianguo
（School of Mechanical Engineering，Inner Mongolia University of Science and Technology，Baotou 014010，China）

To eliminate the effect of the traditional de-noising methods on the edges and details of images during image de-noising，a gaussian noise filtering algorithm based on Pulse Coupled Neural Network（PCNN）time matrix is proposed.The synaptic coupling strength of the PCNN model is defined as a variable whose value is dependent on the similarity among different neurons. Meanwhile，the ignition times of PCNN neurons are recorded in the time matrix.The noise point and the filtering method can be determined according to the corresponding time matrix elements. Experimental results show that the proposed algorithm can filter Gaussian noise effectively，and is more capable for the protection of edges and details of images.

PCNN；time matrix；gaussian noise；synaptic coupling strength；variable value

A

1674-5124（2016）08-0108-05

10.11857/j.issn.1674-5124.2016.08.022

2015-11-10；

2015-12-02

国家自然科学基金（21366017）

内蒙古自治区研究生科技创新资助项目（S20141012711）

内蒙古自治区教育厅自然科学一般项目（NJZY13144）

张文兴（1983-），男，讲师，硕士，研究方向为产品质量建模及控制。