金属粘贴式电阻应变计应变传递分析
王 彪,刘 腾,徐敬龙,刘马宝
(1.西安交通大学航天航空学院,陕西 西安 710049;2.西安交通大学 机械结构强度与振动国家重点实验室,陕西 西安 710049)
金属粘贴式电阻应变计应变传递分析
王彪1,刘腾1,徐敬龙1,刘马宝2
(1.西安交通大学航天航空学院,陕西 西安 710049;2.西安交通大学 机械结构强度与振动国家重点实验室,陕西 西安 710049)
通过建立金属粘贴式电阻应变计的二维应变传递解析计算模型,对金属粘贴式电阻应变计的应变传递机理进行深入分析。结果表明,金属粘贴式电阻应变计的应变传递过程受敏感栅、基底及胶接层的几何参数和物理特性参数影响,且在金属粘贴式电阻应变计敏感栅两端存在应变过渡区。当胶接层横向宽度越宽、厚度越薄、弹性模量越大时,敏感栅两端的应变传递过渡区就越小,金属粘贴式电阻应变计的平均应变传递率则越大。因此,在实际应用中,应优先选择高弹性模量的胶粘剂,且必须严格控制金属粘贴式电阻应变计的粘贴工艺。
金属粘贴式电阻应变计;胶接层;应变传递;测量准确度
0 引言
自20世纪30年代电阻应变计问世以来[1],电阻应变测试技术已被广泛运用于航空航天、交通运输、土木工程、机械工程、能源工程、生物工程以及体育运动等众多领域[2-4]。此外,通过将电阻应变计粘贴在各种弹性敏感元件上,还可以制成测量位移、加速度、力矩、压力等各种物理参数的电阻应变式传感器[5-7],电阻应变式传感器占世界各类传感器总用量的80%以上[7]。
目前,不同种类的电阻应变计已达上万种[7]。其中,金属粘贴式电阻应变计运用最为广泛。在应变测量或电阻应变式传感器制造过程中,金属粘贴式电阻应变计通过α-氰基丙烯酸酯(502快干胶)、环氧树脂、酚醛-缩醛树脂等胶粘剂粘贴在构件或弹性敏感元件的表面[8-9]。当构件或弹性敏感元件受力产生形变时,其变形通过胶粘剂所形成的胶接层传递到金属粘贴式电阻应变计的敏感栅,使敏感栅的阻值发生相应的变化,进而测量构件或弹性敏感元件的应变。然而,由于胶接层的弹性模量与敏感栅的弹性模量之间存在较大的差异,构件或弹性敏感元件的应变并不能全部均匀地传递到金属粘贴式电阻应变计的敏感栅上[10-11]。因此,金属粘贴式电阻应变计的实际测量值与构件或弹性敏感元件的真实应变之间存在一定误差。
针对金属粘贴式电阻应变计的应变传递机理,国外一些学者开展了相关研究。Stehlin[12]通过建立“基体-胶接层-敏感栅”的一维应变传递模型,推导出金属粘贴式电阻应变计敏感栅沿测量轴方向的应变分布公式;Ajovalasit等[13-14]忽略胶接层的影响,得到了应变测量值与真实应变之间的解析关系式,进而对金属粘贴式电阻应变计的应变灵敏系数进行了修正;Zike等[15]利用ABAQUS软件建立了金属粘贴式电阻应变计的二维和三维应变传递模型,对应变传递的影响参数进行了分析,并进行了实验验证。国内一些学者也对金属粘贴式电阻应变计的应变传递机理进行了阐述[16-18],并对胶粘剂的性能及金属粘贴式电阻应变计的粘贴工艺提出了相应要求。但是,从目前已公开的研究报道来看,国内尚未对金属粘贴式电阻应变计的应变传递机理进行较为深入的理论研究。
本文通过建立 “基体-胶接层-基底-敏感栅”的二维应变传递解析计算模型,从理论上分析了金属粘贴式电阻应变计的应变传递机理并得出解析解,同时还具体分析了胶接层参数对应变传递的影响。
1 金属粘贴式电阻应变计的封装结构
图1为典型金属粘贴式电阻应变计的封装结构。金属粘贴式电阻应变计一般由敏感栅、基底、覆盖层及引出线等组成。敏感栅是金属粘贴式电阻应变计最重要的组成元件,它是将应变量转换成电阻变化量的敏感元件,一般由康铜、镍铬合金等金属材料制成,敏感栅的形状与尺寸直接影响到金属粘贴式电阻应变计的性能。基底的作用是保持敏感栅的几何形状和相对位置,并保证将构件上的应变准确地传到敏感栅上。另外,基底还应具有良好的绝缘、抗潮和耐热性能。基底一般由纸、胶膜(环氧树脂、酚醛树脂、聚酰亚胺)、玻璃纤维布等制成。覆盖层可以保护敏感栅免受机械损伤并防止潮气侵入,以保持测量稳定性,通常覆盖层所用胶粘剂与基底胶相同[19]。引出线是用来连接敏感栅和测量电路的过渡导线,一般采用低电阻的镀银铜丝。

图1 典型金属粘贴式电阻应变计的封装结构
金属粘贴式电阻应变计是将应变等机械量转换为电阻变化量的一种传感元件,其工作原理主要是基于金属的电阻-应变效应[7],即当金属丝或金属箔的变形量在一定范围内时,其线应变与电阻变化率之间存在着线性关系:

式中:R——金属丝或金属箔的初始电阻;
ΔR——金属丝或金属箔的电阻变化量;
ε——金属丝或金属箔的线应变;
K——金属丝或金属箔的灵敏系数,它与金属丝或金属箔的电阻率和泊松比有关。
2 金属粘贴式电阻应变计的应变传递分析
本文在分析金属粘贴式电阻应变计的应变传递机理时,作如下假设[11]:1)材料均为线弹性材料,且各向同性;2)基底与覆盖层采用相同的胶粘剂制成,且在测量过程中,敏感栅与基底、基底与胶接层、胶接层与基体的交界面结合紧密,不发生相对滑移;3)基体只承受沿轴向的均匀拉伸应变,且通过胶接层和基底使敏感栅产生形变,敏感栅不直接承受外力;4)不考虑温度变化造成的影响。
图2为金属粘贴式电阻应变计的应变传递解析计算模型。金属粘贴式电阻应变计线栅横截面为矩形,单根线栅的矩形截面尺寸为Wg×Bg;基底和胶接层横向宽度分别为Wm、Wa;线栅和基底纵向长度分别为Lg、Lm;覆盖层、基底和胶接层的厚度分别为Be、Bm、Ba。
如图2(c)所示,以金属粘贴式电阻应变计的敏感栅中心为坐标原点,测量轴方向为x轴,基底及胶接层的厚度方向为y轴建立平面直角坐标系。其中,

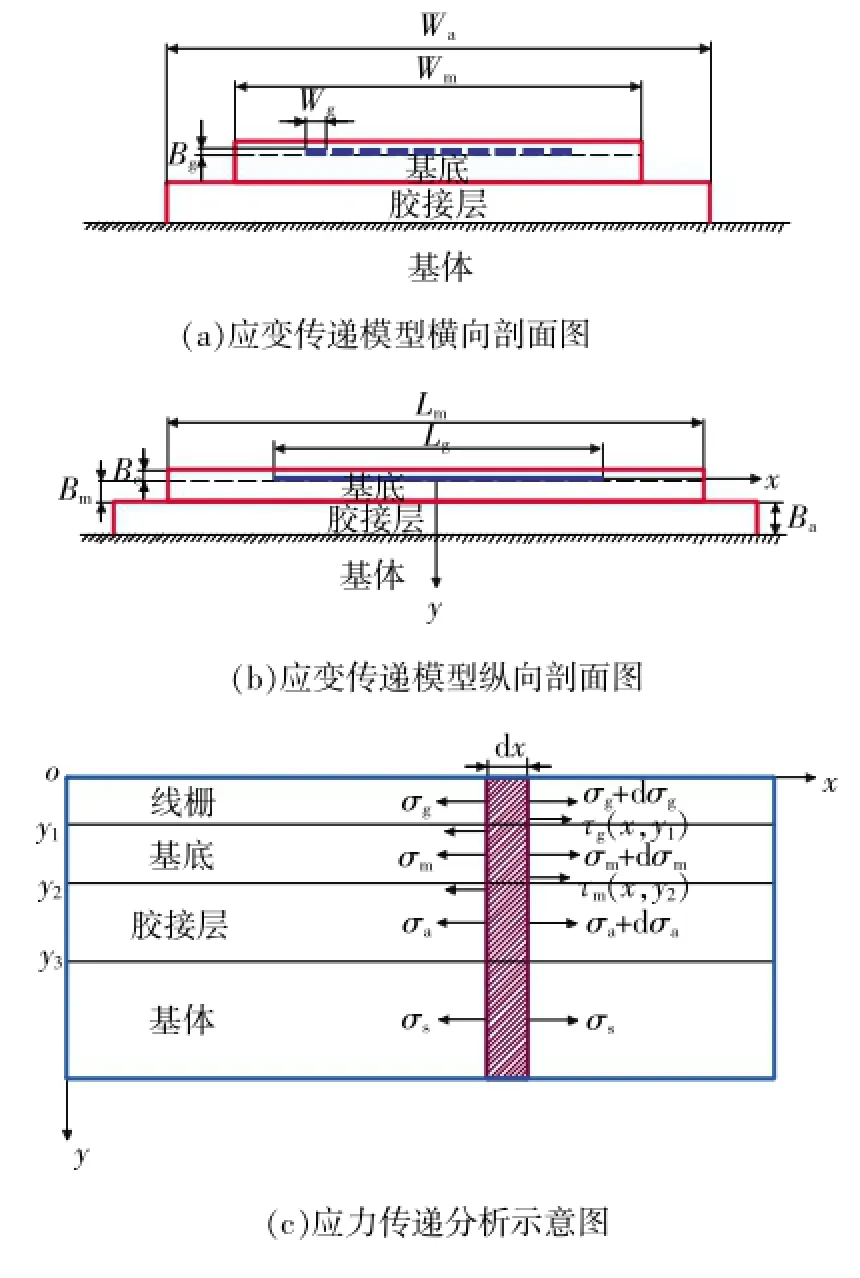
图2 金属粘贴式电阻应变计的应变传递解析计算模型
对线栅、基底和胶接层任取一段微元dx进行受力分析可得:

式中:n——线栅的根数;
将式(2)代入式(3)可得:

根据胡克定律σ=Eε,式(4)和式(5)可以表示为

式中:Eg、Em、Ea——线栅、基底和胶接层的弹性模量;
εg、εm、εa——线栅、基底和胶接层的线应变。
由于线栅、基底和胶接层同步变形,三者应变梯度接近。因此,可以认为

又因为基底和胶接层的弹性模量与线栅的弹性模量相差较大,故:g

将式(8)~式(10)代入式(6)和式(7)可得:a

仅考虑轴向变形,则:

式中:G——材料的剪切模量;
γ——切应变;
u——沿x方向的位移。
将式(13)代入式(11)和式(12)并积分得:

式(14)和式(15)相加得:

求导可得:
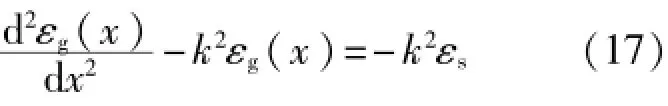
式(17)即为金属粘贴式电阻应变计线栅沿x轴(测量轴)的应变分布的控制方程,其通解为

式中:εg(x)——线栅沿x轴(测量轴)的应变分布;
εs——基体的应变;
C1、C2——待定常数,由边界条件决定。
因为箔栅两端不受力[12],即箔栅两端为自由端面,没有应力传递,故边界条件为

将式(19)代入式(18)中,并令L=Lg,解得积分2常数为

因此,金属粘贴式电阻应变计线栅沿x轴(测量轴)的应变分布为
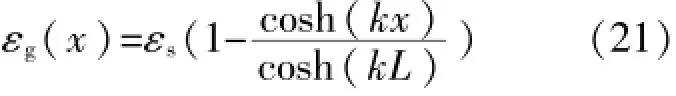
金属粘贴式电阻应变计测量构件或弹性元件的表面应变时,其测量值εm为敏感栅栅长Lg范围内所测量应变的平均值,即:

因此,利用金属粘贴式电阻应变计进行应变测量时,平均应变传递率为
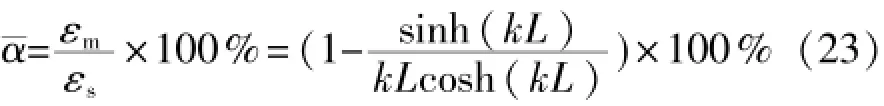
3 胶接层参数对应变传递的影响
通过上述对金属粘贴式电阻应变计的应变传递机理分析可知,将金属粘贴式电阻应变计粘贴在构件或弹性元件表面上测量应变时,影响应变传递的主要因素包括:敏感栅、基底、胶接层的几何参数和物理特性参数。然而,在实际应用中,敏感栅和基底的参数随金属粘贴式电阻应变计的选择而确定。因此,胶粘剂的选择及金属粘贴式电阻应变计的粘贴工艺对应变测量结果的准确性至关重要。为了使金属粘贴式电阻应变计的测量值尽量接近构件或弹性敏感元件的真实应变,减小测量误差,提高测量的准确度,下面就胶接层的几何参数和物理特性参数对金属粘贴式电阻应变计应变传递的影响进行分析。
本文分析时所选用的金属粘贴式电阻应变计的参数如表1所示,金属粘贴式电阻应变计的敏感栅是用厚度为0.005mm的康铜箔制成,基底和覆盖层皆是由环氧树脂制成。

表1 金属粘贴式电阻应变计的参数
3.1应变传递过渡区
若粘贴时所选用的胶粘剂为环氧树脂,且环氧树脂固化后所形成的胶接层的横向宽度Wa=10mm,厚度Ba=30 μm。当基体承受轴向均匀拉伸应变εs=1000μm/m时,分别将上述参数代入式 (22)和Stehlin[12]推导出的应变分布公式中即可得到金属粘贴式电阻应变计线栅沿测量轴的应变分布,如图3所示。
从图中可以看出,式(22)得到的应变分布规律与Stehlin的分析结果基本一致。然而,相较于Stehlin的一维应变传递模型,本文在建立金属粘贴式电阻应变计的应变传递模型时还考虑了胶接层横向宽度对应变传递的影响。因此,本文得到的金属粘贴式电阻应变计线栅沿测量轴的应变分布应更符合真实情况。此外,由图3还可以看出,在金属粘贴式电阻应变计线栅的两端存在应变传递过渡区,而胶接层的参数将直接影响到应变传递过渡区的大小。
图4~图7分析了胶接层参数对金属粘贴式电阻应变计敏感栅两端应变传递过渡区大小的影响。
图4和图5的分析表明,当胶粘剂固化后所形成的胶接层横向宽度越宽,厚度越薄时,金属粘贴式电阻应变计线栅两端的应变传递过渡区就越小。因此,必须严格控制金属粘贴式电阻应变计的粘贴工艺,在保证足够粘接强度和绝缘电阻的前提下,胶接层应尽可能地薄,且胶接层的横向宽度必须大于金属粘贴式电阻应变计基底的横向宽度,一般此外,胶粘剂的选择也至关重要,图6和图7的分析表明,胶接层的弹性模量越大,金属粘贴式电阻应变计的应变传递过渡区就越小,而胶接层的泊松比对应变传递过渡区几乎没有影响。
3.2平均应变传递率
平均应变传递率为金属粘贴式电阻应变计的测量值与构件或弹性敏感元件真实应变的比值,其大小反映了应变测量的准确度。在实际运用中,金属粘贴式电阻应变计通过胶粘剂粘贴在构件或弹性敏感元件表面。因此,金属粘贴式电阻应变计的粘贴质量及胶粘剂的性能将直接影响应变测量的准确度。

图3 金属粘贴式电阻应变计线栅沿测量轴的应变分布

图4 不同胶接层横向宽度Wa时线栅沿测量轴的应变分布

图5 不同胶接层厚度Ba时线栅沿测量轴的应变分布

图6 不同胶接层弹性模量Ea时线栅沿测量轴的应变分布
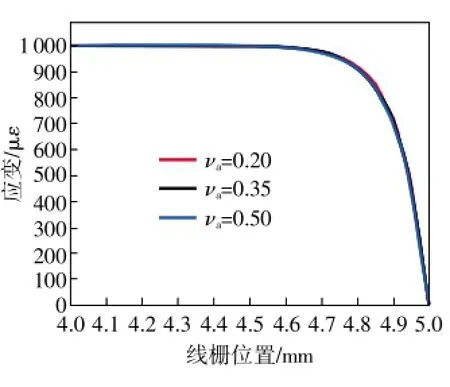
图7 不同胶接层泊松比νa时线栅沿测量轴的应变分布

图8 胶接层横向宽度Wa对平均应变传递率α¯的影响

图9 胶接层厚度Ba对平均应变传递率α¯的影响
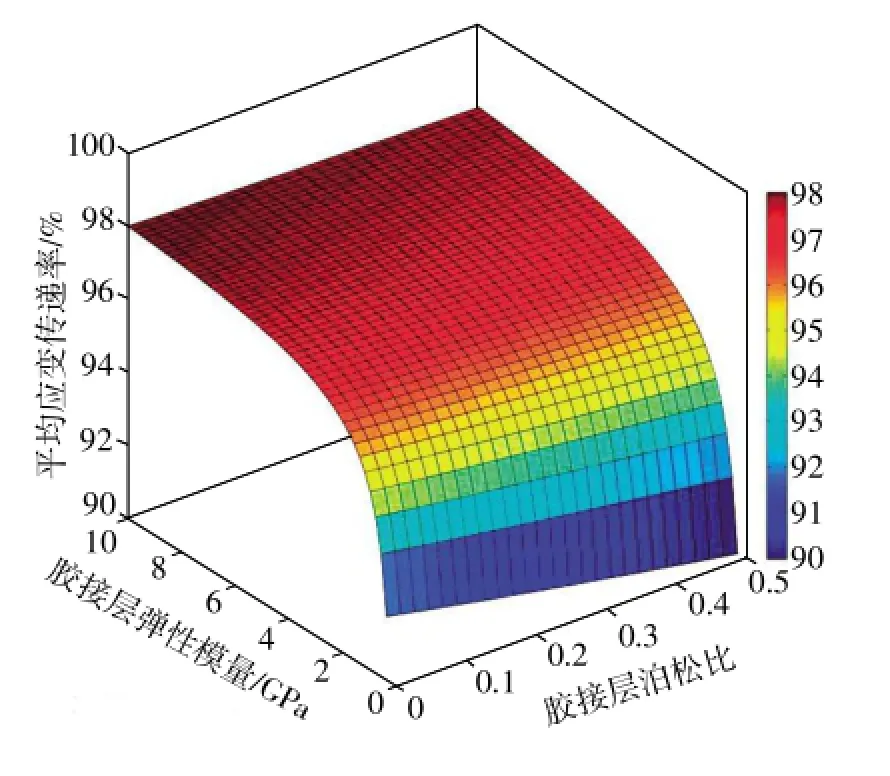
图10 胶接层的弹性常数(Ea、νa)对平均应变传递率α的影响
图8和图9分析了胶接层几何参数对平均应变传递率的影响。结果表明,平均应变传递率随胶接层横向宽度的增大而增大,随胶接层厚度的增大而减小,即胶粘剂涂刷的面积越大,形成的胶接层越薄,越有利于应变传递。但随着胶接层弹性模量的增加,平均应变传递率受胶接层横向宽度和厚度的影响程度逐渐减弱。另外,由图9可以看出,由于金属粘贴式电阻应变计基底的存在,即使在理想粘贴(即胶接层厚度为零)情况下,平均应变传递率并不等于100%,这与实际测量情况相符。因此,本文所建立的应变传递模型比Stehlin[12]和Ajovalasit等[13-14]的应变传递模型更加合理。
目前,可用于电阻应变计粘贴的胶粘剂种类繁多,形成性能各异的胶接层。图10分析了不同弹性模量和泊松比的胶接层对平均应变传递率的影响。从图中可以看出,当胶粘剂固化后所形成的胶接层弹性模量越大,平均应变传递率越大,应力传递效果越好。此外,虽然平均应变传递率随胶接层泊松比增大而减小,但其变化幅值却很小,故在实际应用中可以忽略胶接层泊松比对平均应变传递率的影响。
4 结束语
本文通过建立金属粘贴式电阻应变计的二维应变传递解析计算模型,对金属粘贴式电阻应变计的应变传递机理进行了分析,结果表明:
1)金属粘贴式电阻应变计粘贴于构件或弹性敏感元件表面测量应变时,影响应变传递效果的主要因素有敏感栅、基底、胶接层的几何参数和物理特性参数。
2)在金属粘贴式电阻应变计敏感栅的两端存在应变传递过渡区。当胶粘剂固化后所形成的胶接层横向宽度越宽,厚度越薄,弹性模量越大时,金属粘贴式电阻应变计敏感栅两端的应变传递过渡区就越小。
3)金属粘贴式电阻应变计的平均应变传递率随胶接层横向宽度的增大而增大,随胶接层厚度的增大而减小,随胶接层弹性模量的增大而增大,而胶接层泊松比对平均应变传递率的影响不明显。
综合本文分析可知,在实际应用中,为了使金属粘贴式电阻应变计的测量值尽量接近构件或弹性敏感元件的真实应变,提高测量的准确度,应优先选择高弹性模量的胶粘剂。此外,必须严格控制金属粘贴式电阻应变计的粘贴工艺,在保证足够粘接强度和绝缘电阻的前提下,胶接层应尽可能地薄,且胶粘剂的涂刷面积应大于金属粘贴式电阻应变计基底面积的两倍。
[1] PERRY C C.The resistance strain gage revisited[J]. Experimental Mechanics,1984,24(4):286-299.
[2]MAGUIRE J R,PHILLIPS P.Engineering measurement and testing of land-based structures using strain gauges[J]. Strain,2002,38(2):63-68.
[3]沈观林.应变电测与传感器技术的新发展及应用[J].中国测试,2011,37(2):87-91.
[4]张移山,蔡佳昆,王昊.一种基于串联回路的应变与裂纹综合监测方法[J].电子测量技术,2014,37(8):129-131.
[5]BEDNARZ III E T,ZHU W D.Identifying magnitudes and locations of loads on slender beams with welded and bolted joints using strain gauge-based force transducers with application to a portable army bridge[J]. Journal of Bridge Engineering,2014,19(2):254-265.
[6]RAJANNA K,MOHAN S,NAYAK M M,et al.Pressure transducer with Au-Ni thin-film strain gauges[J]. IEEE Transactions onElectronDevices,1993,40(3):521-524.
[7]张洪润.传感器技术大全(下册)[M].北京:北京航空航天大学出版社,2007:1516-1553.
[8]关明智,王省哲,马力祯,等.液氮低温环境下电阻应变计测试性能的试验研究[J].工程力学,2012(11):350-354.
[9]刘九卿.应变式称重传感器制造工艺及其机理分析[J].衡器,2007(2):9-19.
[10]MORADI M,SIVOTHTHAMAN S.Strain transfer analysis of surface-bonded MEMS strain sensors[J].Sensors Journal IEEE,2013,13(2):637-643.
[11]李东升,李宏男.埋入式封装的光纤光栅传感器应变传递分析[J].力学学报,2005(4):435-441.
[12]STEHLIN P.Strain distribution in and around strain gauges[J].The Journal of Strain Analysis for Engineering Design,1972,7(3):228-235.
[13]AJOVALASIT A,ZUCCARELLO B.Local reinforcement effect of a strain gauge installation on low modulus materials[J].The Journal of Strain Analysis for Engineering Design,2005,40(7):643-653.
[14]AJOVALASIT A,D'ACQUISTOL,FRAGAPANES,et al.Stiffness and reinforcement effect of electrical resistance strain gauges[J].Strain,2007,43(4):299-305.
[15]ZIKE S,MIKKELSEN L P.Correction of gauge factor for strain gauges used in polymer composite testing[J]. Experimental Mechanics,2014,54(3):393-403.
[16]尹福炎,王成林.应变胶粘剂对应变计和传感器性能的影响[J].衡器,2004,33(2):13-22.
[17]尹福炎.电阻应变计与应变传递原理研究[J].衡器,2010(2):1-8.
[18]王健犀.胶粘剂在称重传感器中的应用[J].粘接,2002,23 (6):48-50.
[19]尹福炎.玻璃纤维增强基底全密封结构-制作高稳定性能金属粘贴式电阻应变计的最佳选择 [J].衡器,2007,36 (5):12-15.
(编辑:李妮)
Strain transferring analysis of metallic bonded resistance strain gauges
WANG Biao1,LIU Teng1,XU Jinglong1,LIU Mabao2
(1.School of Aerospace Engineering,Xi'an Jiaotong University,Xi'an 710049,China;2.State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi'an Jiaotong University,Xi'an 710049,China)
A 2D analytical model is proposed to investigate the strain transferring mechanism of the metallic bonded resistance strain gauge.The results show that the strain of the structure cannot be transferred effectively to the grid of metallic bonded resistance strain gauge due to the influence of geometric parameters and mechanical properties of the grid,matrix and adhesive layer,and there are two strain transition regions at both ends of the grid.Moreover,the wider,thinner and stiffer adhesive layer can help decrease the strain transition region and increase the average strain transmission rate.According to the results,conclude that adhesive materials with higher Young's Modulus should be given priority in practical application,and thebonding technology of resistance strain gauges must be strictly controlled.
metallic bonded resistance strain gauge;adhesive layer;strain transferring;measurement accuracy
A
1674-5124(2016)08-0001-06
10.11857/j.issn.1674-5124.2016.08.001
2016-03-10;
2016-04-19
国家自然科学基金项目(51175404)
王彪(1992-),男,云南玉溪市人,硕士研究生,专业方向为飞行器结构健康检测与可靠性。

