基于改进模拟植物生长算法的多层可重构设施布局方法

丁祥海

杭州电子科技大学，杭州，310018



基于改进模拟植物生长算法的多层可重构设施布局方法

丁祥海

杭州电子科技大学，杭州，310018

在对模拟植物生长算法进行改进的基础上，建立了一种多层可重构设施布局方法。该方法引入了空间填充曲线来表征布局方案，可以实现任意两个设施之间的互换，确保设施不被分割；考虑了柔性面积需求、设施形状约束系数、电梯能力约束等因素，使获得的方案更加接近实际情况；建立了以物流成本和重构成本为绩效评价目标的多层可重构设施布局模型；对模拟植物生长算法进行了改进，在此基础上设计了多层可重构设施布局寻优改善算法，该算法具有设置参数简单、全局寻优、搜索速度较快等特点。最后用算例说明了该方法的有效性。

多层可重构设施布局；改进模拟植物生长算法；电梯能力约束；设施形状约束系数

0　引言

为了应对因城市化发展导致土地价格越来越高的现状，大量工厂向垂直方向拓展，多层设施布局问题(multi-floor facility layout problem,MFFLP)成为设施布局问题的重要方面[1-3]。在城市生产环境中生产的产品一般是小型化的，其生产设施逐渐轻型化，可移动性增加，重构成本大幅降低；而城市生产越来越面向顾客，定制化、多品种、小批量是其主要的生产方式[4-6]。在重构成本较低和生产数据不确定(包括产品品种和生产数量)程度高的情况下，适合采用可重构设施布局(reconfigurable facilities layout，RFL)。因此，多层可重构设施布局问题(multi-floors reconfigurable facilities layout problem，MF-RFLP)在城市生产环境中具有广泛的应用需求，它使得这类企业的设施布局由较长期的决策变成短期的对市场需求的一种反应[7-8]。Johnson[1]基于CRAFT研究了多层设施布局问题，但没有考虑电梯的能力，且只有相邻的设施或者面积相等的设施才能实现互换，设施有可能被分割在不同的楼层； Bozer等[9]解决了不同面积设施互换问题和设施被分割问题，但未考虑设施的重构成本和电梯的能力；Mafsuzaki等[10]考虑了电梯能力，但其目的是解决在生产数据确定情况下电梯的数量和位置的决策问题，而多层可重构设施布局往往是电梯能力和位置已知情况下的垂直物流分配问题；Bernardi等[3]建立的多层设施布局问题模型需要设置大量的参数和约束条件，而且其寻优过程是局部的。多层设施布局问题是NP困难的，大量启发式算法应用于多层设施布局问题，如模拟退火法[11-12]、遗传算法[13-14]、禁忌搜索[15]、蛙跳算法[16]、粒子群算法[17]等，其他学者也应用模糊逻辑[18]和专家系统[19]等方法来求解设施布局问题。这些算法通过建立随机性、正反馈性等机制确保以较大概率收敛到全局的最优，但是需要设定一些直接影响收敛性和计算速度的参数，这些参数目前没有通用的选取法则，针对具体问题需要反复摸索。本文分析了可重构设施布局的流程，引入空间填充曲线，并基于空间曲线对多层设施布局问题进行表达，实现任意设施的两两互换；并基于物流和重构成本建立了可重构设施布局的目标函数，基于设施形状约束和电梯能力建立了问题的约束条件；引入形态素因子，对模拟植物生长算法进行改善，提高了算法的寻优速度，并在此基础上设计了多层可重构设施布局的算法；最后，通过一个算例说明了模型的有效性。

1　多层可重构设施布局模型

1.1问题描述

可重构设施布局是指已知下一生产周期的数据(产品品种和数量)情况下，在现有布局的基础上，寻找一种生产绩效最佳的布局方案。其过程一般包括产生可选布局方案、评估方案的绩效和选择并实施方案(图1a)。多层可重构设施布局问题需要同时考虑水平和垂直物流(图1b)，是一个比单层可重构设施布局更复杂的问题。本文进行以下设定。

(1)车间划分为面积相等的网格，引入空间填充曲线，保证车间每个网格的连续性和遍历性[9]。每一层设定一条空间填充曲线，每层的空间填充曲线可以不同，但每层的单个网格面积相等。

(2)网格分配从空间填充曲线的入口端开始，设施之间不留任何网格，没有用完的网格数余留在空间填充曲线的出口端。

(6)设施不能被分割。分配给一个设施的所有网格必须在同一条空间填充曲线上，且所有的网格号是连续的。这个设定保证了设施不会被分割开。设一个设施占有Ai个网格，其网格编号依次为(a，a+1，…，i，j，…，b)，则应满足:j=i+1,b-a+1=Ai(a,b=0,1,…,N；N为所在楼层可分配的空间曲线的最大网格编号)。

(7)拆卸、搬运和安装是产生设施重构费用的主要动因。在多层可重构设施布局中，搬运既包括垂直方向的运动，又包括水平方向的运动。在整个设施重构费用中，水平方向运动产生的费用所占比重小，因此，本文设定设施在同层楼重构时，其重构费为一定值，与重构前后的位置无关；设施在不同楼层之间重构时，其重构费用只与重构前后的楼层相关，与所在楼层的具体位置无关。

(a)可重构设施布局过程

(b)可重构设施布局问题中的物流图1　多层设施可重构布局

1.2模型的构建

可重构设施布局的绩效不仅包括物流成本和重构成本，而且包括在制品库存、周期时间、生产提前期等绩效指标。目前关于布局与在制品库存、周期时间和生产提前期等绩效指标的内在联系的研究尚不充分[7]。本文方法只考虑重构成本和物流成本，取两者的和为目标函数，即

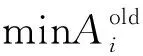
(2)

设施之间、设施与电梯之间的水平距离可以由网格编号与网格座标方便求得，不再赘述。

2　基于改进模拟植物生长算法的MF-RFLP求解算法

2.1模拟植物生长算法及其可能存在的问题

模拟植物生长算法(PGSA)是李彤等[20-21]提出的基于植物向光性机理的智能优化算法，最初用于解决非线性整数规划问题，由于其对参数的确定极为简单和宽松，同时具备全局寻优性质，故在电网规划[22]、设施选址[23]、地下物流[24]等工程技术领域获得应用，并取得了较好的效果。本文用其解决MF-RFLP，是一种新的尝试。

PGSA的核心问题包括两个方面，一是形态素浓度的计算方法，二是生长点的选择。已经扩展但没有长出新节点的叶节点，其形态素为0，其他叶节点的形态素计算公式为

(3)

其中，pi为节点Si的形态素浓度，f(Si)为节点Si的目标函数值，f(S0)为起始节点S0的目标函数值。生长节点的选择是通过构建pi在[0,1]的状态区间，利用计算机产生随机数，依据随机数所在的区间来进行的。当解空间中节点数量比较多时，收敛速度慢是模拟植物生长算法存在的主要问题。

2.2模拟植物生长算法的改进

2.3设施互换准则和算法

2.3.1设施互换准则

准则1任意设施两两互换是产生新节点的基本方法。既要考虑面积相等设施之间的互换和相邻设施之间的互换，又要考虑面积不相等的不相邻的设施之间的互换。

准则2面积不相等的不相邻的设施互换时可能产生设施重构的传导效应，每个波及到需要重构的设施只需满足该设施的最小需求面积。

准则3当发生设施重构波导效应有多个重构方案时，选择重构费用最小的方案。

2.3.2同层设施互换算法

图2　同层设施互换

(1)如果Ai=Aj，则平稳互换，Aj→Ai,Ai→Aj。其他设施不需移动。

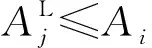
2.3.3不同层设施互换算法

图3　不同楼层的设施互换

(1)如果s(g)=s(h) ，设施在同一楼层，设施互换可以进行。

(2)如果s(g)≠s(h) ，设施不在同一楼层，则需要考虑两个设施的面积：

①如果Az(i)=Az(j)，则可以平稳互换；

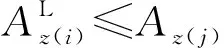
当设施互换可以进行，但需要移动其他设施时情况比较复杂，下面做进一步分析。

2.4设施形状约束系数算法

2.5改进模拟植物生长的MF-RFLP算法

在模拟植物生长算法中，按照形态素浓度是否为零可以将节点分为两类：一类是已扩展的节点，这类节点形态素为0；另一类是尚未扩展的节点，这类节点形态素大于或等于0。因此，建立Open表和Closed表，Open表用来储存尚未扩展的叶节点，Closed表储存已经扩展的节点，包括根节点、枝节点和不能产生新的合格节点的叶节点(图4)。

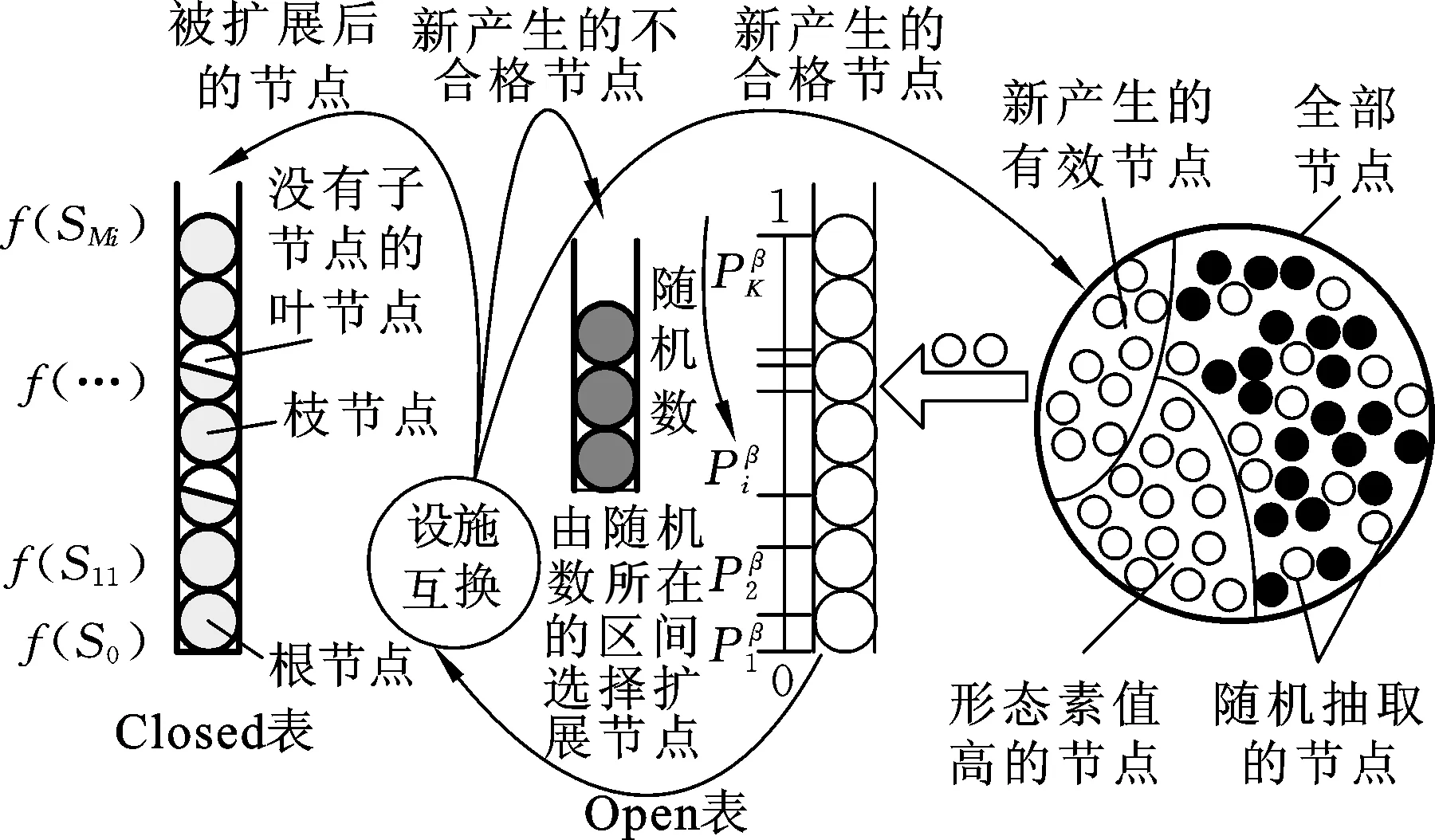
图4　改进的模拟植物生长算法模型

基于模拟植物生长算法的车间设施布局改善具体流程如下。

(1)基础数据输入。①车间网格数据，包括网格编号、网格坐标、网格面积等；②设施基本数据，包括设施的最小面积、最大面积、形状约束值、重构费用等；③物流数据，包括设施之间的物流量、单位物流费用等；④现有布局方案，包括设施的顺序，以及每个设施占有的面积(网格数)等；⑤算法参数设置，参数包括最大扩展次数，形态素因子β等。

(2)计算原始布局的费用f(S0)，建立树根，令max=f(S0)。

(3)设施互换(图4)。将合格的节点存入Open表，将不合格的节点舍弃；选择形态素值高的节点存入Open表；在剩余节点中随机抽取部分节点存入Open表；将已扩展节点从Open表中移到Closed表中。节点是否合格的判定方法如下：①节点为新节点；②节点满足形状约束；③节点费用小于父节点费用；④方案垂直物流需求满足电梯能力约束。

(4)判断。若Open表不为空且扩展次数小于预定值，则计算形态素，产生随机数，选定待扩展节点，执行步骤(3)；若Open表为空或者扩展次数等于预定值，输出最小费用方案，停止计算。

以上所有算法用MATLAB 7.10编程实现。

3　算例及分析

为了对提出的方法进行比较，本文提供两个算例。第一个算例比较了模拟植物生长算法改进前后的效果，第二个算例比较了I-PGSA、CRAFT和MULTIPLE三种方法的优劣。

3.1模拟植物生长算法改进前后的效果比较

设某小型电动工具装配企业车间分布在一个两层楼的建筑物内，第一层的有效面积为64个网格，第二层楼的有效面积为56个网格，楼层高度为5 m。其空间填充曲线、相应的网格编号及其坐标如图5所示。有3个电梯，1号和2号电梯的能力为100箱/天，3号电梯的能力为120箱/天，电梯位置如图6所示，生产周期为10天。所有设施的形状系数设定为1.2，最小面积见表1，其物流数据见表2。为方便计算，水平物流的费用为1元/箱米、垂直物流为5元/箱米。原始方案的目标函数值为167 710元。设定同一层楼的重构费用为600元、不同层重构费用为1300元，扩展的次数为300。应用PGSA运算了3次，获得最小目标值为125 146元，对应的布局方案如图7所示；应用I-PGSA运算了3次，获得最小目标值为100 120元的改善方案如图8所示。结果表明I-PGSA比PGSA具有更快的收敛速度。

图5　空间填充曲线及其编号与坐标

图6　设施的初始布局

(网格个数)

表2　设施之间的物流量

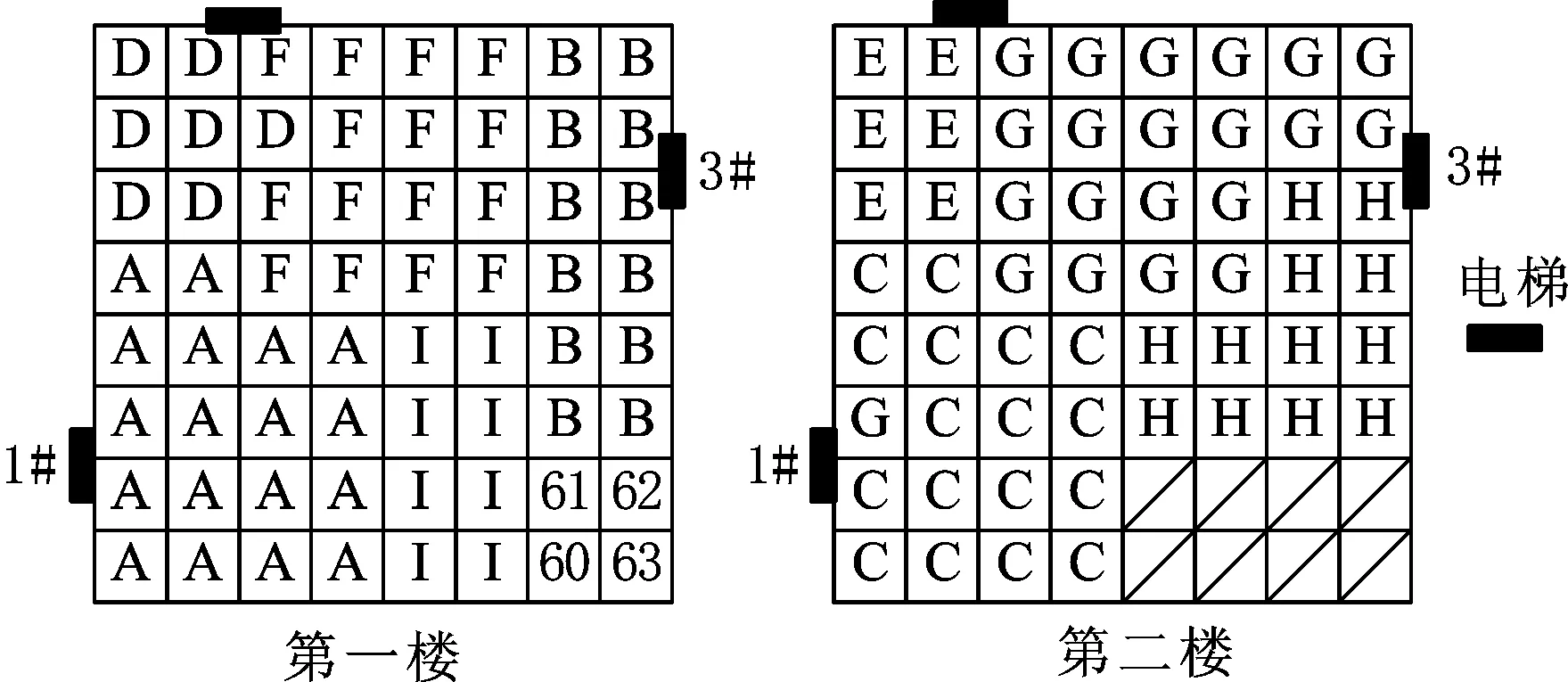
图7　PGSA扩展300次的布局方案

图8　改善模拟植物生长算法扩展300次的布局方案

3.2与CRAFT和MULTIPLE方法的比较分析

CRAFT和MULTIPLE是两种主要的布局方法，许多软件都是基于这两种方法开发的。本文采用文献[9]中的数据和空间填充曲线，应用所建立的方法进行求解，并与CRAFT和MULTIPLE方法进行比较。因为设施O的位置不能改变，本文令设施O的重构成本为一个较大的值(100 000元)，形状约束系数为1，其他设施形状约束系数定为1.25，扩展次数为10。所得结果见表3。本文方法对应的布局方案如图9所示。

表3　三种方法运算结果

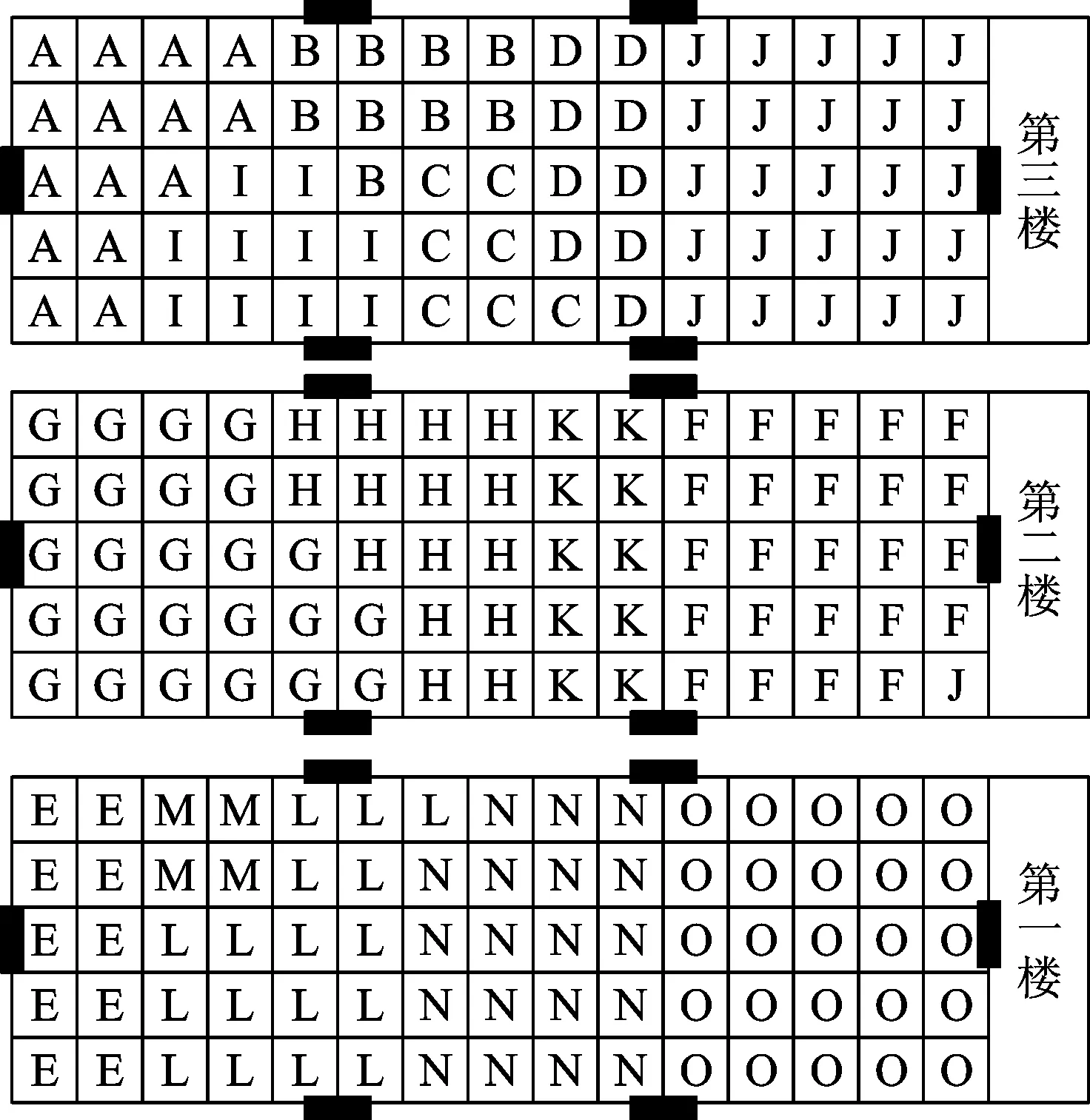
图9　改善后的布局方案

CRAFT方法只考虑了面积相等的设施或者相邻设施的互换，而且设施有可能被分割在不同的楼层，故其运算速度较快，所需时间少。MULTIPLE方法考虑了面积不相等设施之间的互换，比CRAFT方法考虑了更多的方案，但在处理设施重构波动效应时，没有遵循重构成本最低原则，而是采用近似平均分配网格的方法，这样提高了整个方案的重构成本，这是其获得的目标值大于本文所提方案获得的目标值的主要原因。另外，MULTIPLE方法没有考虑电梯的能力。本文方法既考虑了面积不相等设施之间的互换，同时考虑了电梯的约束，虽然运行时间稍多于CRAFT方法和MULTIPLE方法的运行时间，但是获得的布局方案目标值明显优于另外两种方法获得的布局方案目标值。

4　结论

(1)每层楼分别建立空间填充曲线，并按空间填充曲线确定的顺序给设施分配面积，利用空间填充曲线的连续性，保证了设施不会被分割。

(2)考虑了不同面积的设施交换时可能产生的设施重构传导效应，并通过引入设施的柔性面积需求，减小了这种效应的影响。

(3)对模拟植物生长算法进行了改进。通过建立解空间子集和引入形态素因子，加快了算法的收敛速度，同时保证了算法搜索的全局性。

(4)MF-RFLP是在土地成本增加、产品小型化和个性化、生产数据多变的城市生产环境下的一个生产运作管理问题。本文方法综合考虑了物流成本和重构成本、形状约束和电梯能力等方面，使得模型更加接近实际情况，所得方案具备更高的可行性。建立的MF-RFLP改进模拟植物生长算法具有参数简单和较好的全局搜索能力。本文的不足在于在建立目标函数时，只考虑了物流成本和重构成本，没有考虑面积使用成本，也没有考虑在制品库存、系统产出率、提前期等指标，今后将开展这些方面的研究。

[1]Johnson R V.Spacecraft for Multi-floor Layout Pla-nning[J]. Management Science,1982,28(2):407-417.

[2]Izadinia N,Eshghi K,Solmani M H.A Robust Mo-del for Multi-floor Layout Problem[J].Computers & Industrial Engineering,2014,78(12):127-134.

[3]Bernardi S,Anjos M F.A Two-stage Mathematical-programming Method for the Multi-floor Facility Layout Problem[J].Journal of the Operational Research Society,2013,64(3):352-364.

[4]封海波.上海都市型工业空间组织探讨[J].城市研究,2014(6):129-133.

Feng Haibo.Discussion on Urban Industrial Space Organizations of Shanghai[J].City Study, 2014(6):129-133.

[5]王磊，付建荣.美国都市工业的空间分布及其对中国城市发展的启示[J].经济地理,2014,34(8)：81-88.

Wang Lei, Fu Jianrong.The Spatial Distribution of Urban Manufacturing Industries in the United States and Its Implications for Urban Development in China[J].Economic Geography, 2014,34(8)：81-88.

[6]Spath D,Lentes J.Urban Production to Advance the Competitiveness of Industrial Enterprises[C]// Challenges for Sustainable Operations.International Conference on Production Research.Iguassu Falls,2013:1-5.

[7]Meng G,Heragu S S,Zijm H.Reconfigurable Layout Problem[J].International Journal Production Research,2004,42(22):4709-472.

[8]金哲，宋执环，杨将新.可重构制造系统工艺路线与系统布局设计研究[J].计算机集成制造系统，2007,13(1)：7-12.

Jin Zhe, Song Zhihuan, Yang Jiangxin. Process Route and Layout Design Method for Reconf-igurable Manufacturing Systems[J].Computer Integrated Manufacturing Systems,2007,13(1)：7-12.

[9]Bozer Y A,Meller R D,Erlebacher S J.An Improvement-type Layout Algorithm for Single and Multiple-floor Facilities[J].Management Science,1994,40(7):918-932.

[10]Matsuzaki K, Irohara T, Yoshimoto K.Heuristic Algorithm to Solve the Multi-floor Layout Problem with the Consideration of Elevator Utilization[J].Computers & Industrial Engineering,1999,36(2):487-502.

[12]Ghadikolaei Y K, Shahanaghi K, Ghadikolaei Y K, et al. Multi-floor Dynamic Facility Layout: A Simulated Annealing-based Solution[J]. International Journal of Operational Research, 2013, 16(4):375-389.

[13]Aiello G, Scalia G L, Enea M. A Non Dominated Ranking Multi Objective Genetic Algorithm and Electre Method for Unequal Area Facility Layout Problems[J].Expert Systems with Applications,2013, 40(12):4812-4819.

[14]Pourvaziri H, Naderi B, Pourvaziri H, et al. A Hybrid Multi-population Genetic Algorithm for the Dynamic Facility Layout Problem[J]. Applied Soft Computing, 2014, 24(24):457-469.

[15]Scholz D, Petrick A, Domschke W. STaTS: A Sl-icing Tree and Tabu Search Based Heuristic for the Unequal Area Facility Layout Problem[J]. European Journal of Operational Research, 2009, 197(1):166-178.

[16]刘琼，许金辉，张超勇.基于改进蛙跳算法的鲁棒性车间布局[J].计算机集成制造系统,2014, 20(8):1879-1886.

Liu Qiong，Xu Jinhui，Zhang Chaoyong.Robust Layout of Floor Shop Based on Improved Shuffled Frog Leaping Algorithm[J].Computer Integrated Manufacturing Systems,2014,20(8):1879-1886.

[17]Samarghandi H,Taabayan P, Jahantigh F F.A Par-ticle Swarm Optimization for the Single Row Facility Layout Problem[J]. Cpmputer & Industrial Engineering ,2010,58(4):529-534.

[18]武志军，宁汝新，王爱民.可重构制造系统布局规划方案的灰色模糊综合评价方法[J].中国机械工程，2007,18(19):2313-2318.

Wu Zhijun,Ning Ruxin,Wang Aimin.Grey Fuzzy Synthetically Evaluation Method for RMS Layout Planning[J].China Mechanical Engineering, 2007,18(19):2313-2318.

[19]García-Hernández L, Palomo-Romero J M, Salas-Morera L, et al. A Novel Hybrid Evolutionary Approach for Capturing Decision Maker Knowledge into the Unequal Area Facility Layout Problem[J].Expert Systems with Applications, 2015, 42(10):4697-4708.

[20]李彤, 王春峰, 王文波, 等.求解整数规划的一种仿生类全局优化算法[J].系统工程理论与实践,2005,25(1):76-85.

Li Tong, Wang Chunfeng, Wang Wenbo, et al.A Global Optimization Bionics Algorithm for Solving Integer Programming-plant Growth Simulation Algorithm[J].System Engineering Theory and Practice,2005,25(1):76-85.

[21]李彤，王众托. 模拟植物生长算法与知识创新的几点思考[J].管理科学学报,2010,13(3):87-96.Li Tong, Wang Zhongtuo.Plant Growth Simulation Algorithm and the Thinking in Knowledge Innovation[J]. Journal of Management Sciences in China, 2010,13(3):87-96.

[22]王淳，程浩忠. 基于模拟植物生长算法的配电网重构[J].中国电机工程学报,2007,27(9)：50-55.

Wang Chun,Cheng Haozhong.Reconfiguration of Distribution Network Based on Plant Growth Simulation Algorithm[J]. Proceedings of the CSEE, 2007,27(9)：50-55.

[23]李彤，王众托.模拟植物生长算法在设施选址问题中的应用[J].系统工程理论与实践,2008,28(12)：107-115.

Li Tong, Wang Zhongtuo.Application of Plant Growth Simulation Algorithm on Solving Facility Location Problem[J]. System Engineering Theory and Practice, 2008,28(12)：107-115.

[24]李彤，王众托. 大型城市地下物流网络优化布局的模拟植物生长算法[J].系统工程理论与实践，2013,33(4)：971-980.

Li Tong, Wang Zhongtuo.Optimization Layout of underground Logistics Network in Big Cities with Plant Growth Simulation Algorithm[J]. System Engineering Theory and Practice, 2013,33(4)：971-980.

(编辑陈勇)

Multi-floor Reconfigurable Facility Layout Method Based on Improved Plant Growth Simulation Algorithm

Ding Xianghai

Hangzhou Dianzi University, Hangzhou, 310018

A method of multi-floor reconfigurable facility layout was presented based on improved plant growth simulation algorithm. According to the features of multi-floor reconfigurable facility layout problem, spacefilling curves were used to describe the facility locations, making it possible to exchange any two facilities. Flexible area requirements, shape constraints and elevator utilization were used to keep the layout solution’s feasibility. Considering the material handle costs and facility reconfigurable costs together, a performance evaluation model was constructed. Based on the improved plant growth simulation algorithm, the performance improvement algorithm was developed. At last, two examples were presented to show the accuracy and generalization of this method.

multi-floor reconfigurable facility layout；improved plant growth simulation algorithm；elevator capacity constraint；facility shape constraint coefficient

2015-10-09

浙江省自然科学基金资助项目(LY13G010007)；国家社会科学基金资助项目(15BGL100)；NSFC-浙江两化融合联合基金资助项目(U1509220)；浙江省人文社科基地重点项目(ZD05-2016ZB)；浙江省哲学社会科学重点研究基地浙江省信息化与经济社会发展研究中心项目(15XXHJD11)

TH66DOI：10.3969/j.issn.1004-132X.2016.15.007

丁祥海，男，1971年生。杭州电子科技大学工业工程与管理研究所副教授、博士。主要研究方向为城市生产、装配系统规划等。