基于VMI的车辆器材供应链收益共享协调
文正中, 王 亮, 何 健, 张大鹏
(1. 军事交通学院研究生管理大队, 天津 300161; 2. 军事交通学院军用车辆系, 天津 300161)
基于VMI的车辆器材供应链收益共享协调
文正中1, 王亮2, 何健1, 张大鹏2
(1. 军事交通学院研究生管理大队, 天津 300161; 2. 军事交通学院军用车辆系, 天津 300161)
为了合理地分配军事供应链系统实施供应商管理库存(Vendor Management Inventory,VMI)策略后所取得的收益,建立了传统模式、基于Stackelberg博弈和基于纳什均衡协商的收益共享协调模型来协调VMI,并进行了实例分析。结果表明:传统的VMI模型缺乏合理性和可操作性;Stackelberg博弈模型能使军供双方各自的收益有一定的提高,但供应链的整体收益不能最大化;纳什均衡协商模型不但能使军供双方各自的收益有所改善,实现双赢,而且还能使供应链整体收益达到帕累托最优。
供应商管理库存; 收益共享协调; Stackelberg博弈; 纳什均衡协商
供应商管理库存(Vendor Management Inventory,VMI),也称寄销库存,是一种供应链环境下的库存运作模式。与传统库存管理模式相反,VMI是以销售商和供应商双方都获得最低成本为目的,在一个共同的协议下由供应商对库存进行管理,并不断地监督协议的执行情况,修正协议内容,使库存管理得到持续改进的合作性策略。军事供应链中的VMI是指军方车材采购中心(下文简称“军方”)与供应商在一个共同的协议下,军方将库存决策权交给供应商,由供应商管理甚至拥有军方的库存,在保障部队用户的过程中,军方为供应商提供部队用户的需求信息,以便其合理地确定总的库存水平[1]。
基于供应链管理思想的VMI追求的是双赢,只有实现军事供应链整体效益与军地双方各自的利益同时增加,才有利于合作关系的稳定发展。在军事供应链中采用VMI,可有效地促进信息分享,降低牛鞭效应和供应链的库存成本,从而提升军事供应链的整体保障效益。但由于军方的库存成本转移给了供应商,使供应商的库存成本增加,可见军事供应链整体效益的提高并不代表军供双方的利益都会得到相应的提高。因此,军方为吸引供应商积极参与VMI,必须建立军地之间的利益协调机制,通过制定合理的收益分配方案,将军方节省的部分成本补偿给供应商,使供应商获得相应的收益,进而保证军事供应链中各成员间协同,整体稳定、成功地运作。
如何保证供应链成员的互利性是VMI实施的动力源泉,也是目前研究的热点之一。收益共享机制是通过制定供应链总收益在成员间的收益分配关系,实现供应链系统的协调。研究表明:收益共享机制是VMI实施过程中协调供应商和零售商之间的有效方式。Gerard等[2]研究了收益共享契约的优点和不足,以及收益共享契约如何通过决策零售商的最优价格和订货量来协调供应链系统,并分配其利润的问题。Wang等[3]研究了一个基于收益分享契约的VMI模型,其中,零售商占Stackelberg博弈的主导地位,分析了当需求函数为和形式、乘积形式时零售商对收益份额的最优决策,以及国内供应商对库存量和零售价的最优决策;但未进一步对契约进行优化,也未探讨如何实现供应链协调。蔡建湖等[4]通过零售商向供应商支付剩余补贴的方式实现双方期望收益的帕累托改进,并实现了供应链协调。曹武军等[5]在假设市场需求是价格敏感的随机变量的情况下,利用收益共享机制来协调VMI模式下供应链各成员之间的合作关系。杨潮兴等[6]针对军事装备供应链中军地通用装备的采购,研究了 VMI 实施的条件及相应的价格契约,设计了简单的价格补贴,并通过算例对结果进行了验证。刘鹏飞等[7]研究了随机需求下的供应商管理库存模型,通过调节收益共享系数实现供应链成员收益的分配;但该模型假设产品的残值为0,没有考虑缺货产生的损失。Yu等[8]研究了由单个供应商服务多个零售商的VMI模型,提出并通过实例证明只要双方接受一个既定的收益共享系数,就能使双方收益都得到提高。总之,以上研究从多个方面阐述了收益共享机制的具体实施方式,但上述收益共享契约的设计普遍对市场需求进行了许多限制,如需求严格服从正态分布,不考虑缺货情况等,考虑到军事供应链的特殊性,上述模型并不适用于建立军事供应链VMI模型。
为此,笔者综合考虑军事供应链中部队用户的实际需求情况,假设车辆器材的需求服从均匀分布,并考虑可能存在的缺货情况,给出了集中式和分散式供应链下VMI的最优订货量和最优收益,分别建立了传统模式、基于Stackelberg博弈和基于纳什协商的VMI收益共享模型对供应链进行协调,最后通过实例对相关结论进行了验证。
1 供应链结构模型
在军事供应链中应用VMI策略后,车辆器材的产权属于供应商并存放于供应商仓库,军方没有车辆器材的所有权,并由供应商根据军方需求预测情况进行生产和存货管理。当军方产生需求时,供应商根据订单将车辆器材配送至指定地点,军方实现了“零库存”,减少了军事供应链的冗余环节,消除了重复性工作,实现了供应链集成化管理要求;同时,也缩短了保障距离和保障时间,减少了车辆器材周转次数。由于军方是军用车辆器材保障的权力部门,因此部队用户产生需求后须通过军方提供给供应商,然后由供应商将恰当数量、合格质量的车辆器材在恰当的时间配送给部队用户。基于VMI的车辆器材供应链结构模型如图1所示。

图1 基于VMI的车辆器材供应链结构模型
笔者以单周期供应链模型为研究对象,其由一个生产某种单周期车辆器材的供应商、一个军方车辆器材采购中心和部队用户构成。在随机需求条件下,供应商对部队用户车辆器材需求进行预测,并据此确定库存系统的需求,进行库存量决策[9]。当部队用户的实际需求大于供应商的库存量时,军方会因缺货而不能进行正常的车辆器材维修保障,且实际需求越大,车辆器材缺货越多,缺货损失也越大;当军方需求量小于供应商的库存量时,供应商的仓库产生库存积压,且部队用户的实际需求越小,库存积压越多,供应商的收益就越小,通常未消耗的车辆器材残值归供应商所有。
2 模型构建
2.1模型假设
为了研究方便,对军事供应链进行如下假设:

2)对于同类车辆器材,供应商的单位车辆器材生产成本不变;
3)该供应商在全国各地都建有配送网点,车辆器材可直接配送至与各配送网点相邻的部队仓库或用户,订货和配送成本忽略不计。
对模型中涉及的参数定义如下:q为军方对某种车辆器材的订货量;c为单位车辆器材的生产成本;w为单位车辆器材的批发价;p为单位车辆器材所产生的军事收益;hs为未消耗的车辆器材在各阶段的单位库存管理费用;l为供应商耗费的单位缺货成本;v为未消耗的车辆器材的残值,并假定p>w>c>v,则车辆器材的期望消耗量S(q)为

(1)
车辆器材的期望库存量I(q)为
I(q)=E((q-D)+)=q-S(q)=

(2)
车辆器材的期望缺货量L(q)为
L(q)=E((D-q)+)=E(d)-S(q)=

(3)
由于随机需求服从均匀分布,将式(1)-(3)整理可得

2.2VMI效益模型
2.2.1集成式VMI供应链模型
集成式VMI供应链以整体期望收益最大进行决策,是分散式VMI供应链追求的最优目标。集成VMI供应链中供应商和军方作为一个整体进行决策[10],确定最优订货量,使整体收益最大,集成VMI供应链整体期望收益πt为

(4)
将式(1)-(3)代入式(4),可得
πt=pS(q)-hsI(q)+vI(q)-lL(q)-cq=

(5)
为使集中决策下的整合模型达到最优的订购点,须满足

整理可得集中式VMI最优订货量为

(6)
供应链整体的最优收益为

(7)
2.2.2分散式VMI供应链模型
分散式VMI供应链中供应商和军方分属于不同的实体,供应商决定车辆器材的库存补给量,并使其期望收益最大,主要负责对军方的库存进行监控及执行补货决策,并承担相应的缺货损失和库存管理成本。此模式下军供双方的期望收益πa和πs分别为

(8)

(9)
在分散决策下,供应商为了使自身的效益最大化,须满足

整理后可得分散式VMI的最优订货量为

(10)


(11)

(12)
分散式VMI供应链最优期望收益为

(13)
2.3基于VMI的收益共享协调模型
传统VMI中,由于军方在实施VMI初始阶段,订货成本不会发生较大变化,导致供应商在成本增大的情况下收益可能无明显提高,但却要承担相应的库存管理成本和缺货成本,极大地影响了供应商参与VMI的积极性,也影响了供应链的协调性。笔者引入收益共享机制来达到提升供应商积极性和供应链协调性的目的。
在收益共享契约下,设λ为军供双方的收益共享系数,即部队用户每消耗一单位的车辆器材,军方保留λp收益,剩余的(1-λ)p收益归供应商所有,且0≤λ≤1。其中πs(λ,q)和πa(λ,q)分别为供应商和军方在收益共享系数为λ、订货量为q时的收益函数。
2.3.1传统VMI模式下的收益共享协调
在传统VMI中,军供双方的效益函数分别为

(14)
πs(λ,q)=(1-λ)pS(q)-(hs-v)I(q)-
lL(q)-cq=[(1-λ)p+l-c]q-

(15)


(16)

(17)
显然,依据该共享机制,供应链不可能达到协调,虽然军事供应链的整体效益达到了集中决策下整体效益的最优状态,但供应商攫取了全部效益。因此,传统VMI模式下的收益共享协调机制难以实施。
2.3.2基于Stackelberg博弈的VMI收益共享协调
在VMI实施过程中,一般军方是占主导地位,军供双方共享信息,这可看作是二人进行的Stackelberg博弈[11],其中军方是主导方,供应商是跟随方。其博弈过程可描述如下:

2)由占主导地位的军方选择一个最优的收益分享系数,供应商将在λ下的收益与其预期收益相比较,选择是否接受,在供应商作出决策后,博弈结束。若接受,则该收益共享机制达成,此时军供双方的新收益分别为πa(λ2,q2)和πs(λ2,q2)。
该博弈过程的数学过程可表示为

(18)

为最大化自己的收益,供应商根据式(10)确定最优库存补给量为

(21)
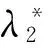
(22)

(23)

(24)
2.3.3基于纳什均衡协商的VMI收益共享协调
纳什均衡协商是一种组合策略,可使每个参与者的策略是对其他参与者策略的最优反应。换言之,如果在一个策略组合上,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。


(25)

(26)

(27)
其中:

(28)

(29)
将纳什均衡协商优化模型转化为非线性规划问题,可得

(p+l+hs-v)-dl/2-[(1-λ)p+l+
hs-v](p+l-c)2d/[2(p+l+hs-v)2]-


(30)
该非线性规划问题的目标函数和约束函数的梯度为




令δ1=δ2=0,可得

(31)



由此可见:通过基于纳什均衡协商的VMI协调,军事供应链系统的最优库存补给量和最优收益达到了集中决策下的最优水平,且军供双方各自的收益都高于基于Stackelberg博弈收益共享协调下的收益水平。
3 实例分析
军方与某家生产某种车辆器材的供应商合作实施VMI,军方需求x服从均匀分布,x~U(0,2 000),供应商的生产成本为c,并以批发价w向军方供应车辆器材。当供大于求时,未消耗车辆器材的残值v归供应商所有;当供不应求时,供应商产生缺货损失l[13]。运用MATLAB软件,分析车辆器材的供应价格、单位车辆器材的生产成本等参数的变化对库存补充量、收益共享系数、军供双方各自的收益以及供应链整体收益的影响,传统VMI模式下、基于Stackelberg博弈和基于纳什均衡协商的VMI收益共享协调分析结果分别如表1-3所示。

表1 传统VMI模式下的收益共享协调分析结果

表2 基于Stackelberg博弈的VMI收益共享协调分析结果

表3 基于纳什均衡协商的VMI收益共享协调分析结果

4 结论
笔者在收益共享机制下建立了一个需求服从均匀分布且考虑缺货成本的车辆器材供应链VMI模型,构建了传统模式下、基于Stackelberg博弈和基于纳什均衡协商的收益共享协调模型来协调VMI,并进行了实例分析。结果表明:在本文的需求假设下,纳什均衡协商模型与传统模式和Stackelberg博弈模型相比,能使军事供应链的收益达到最优且可提高军供双方的收益。
收益共享机制的实施不但能有效协调VMI供应链,合理地分配VMI供应链的收益,且有利于提高供应商参与VMI的积极性。但目前的研究还停留在信息对称、一对一的简单模型上,下一步将在信息不对称、多对多以及多阶段、多周期等更加复杂的供应链情形下,对VMI系统模型收益共享机制的适用和实施情况进行分析和研究。
[1]王丰,汪贻生,王开勇.军事供应链理论与应用[M].北京:物资出版社,2010:96-97.
[2]Gerard P C,Martin A L. Supply Chain Coordination With Revenue-sharing Contracts:Strengths and Limitations[J]. Management Science, 2005, 51(1):30-44.
[3]Wang Y Z,Jiang L,Shen Z J.Channel Performance under Consignment Contract with Revenue Sharing[J].Management Science, 2004,50(1):34-37.
[4]蔡建湖,黄卫来,周根贵.基于收益分享契约的VMI模型研究[J].中国管理科学,2006,14(4),108-113.
[5]曹武军,李成刚,王学林.VMI环境下收入共享契约分析[J].管理工程学报,2007,21(1):51-55.
[6]杨潮兴,张志峰,李保华.装备供应链价格补偿契约实施VMI分析[J].物流科技,2008,31(11):126-128.
[7]刘鹏飞,谢如鹤,刘广海.基于收益共享机制的VMI协调[J].系统工程,2008,26(7):81-85.
[8]Yu Y, Chu F, Chen H. A Stackelberg Game and its Improvement in a VMI System with a Manufacturing Vendor[J].Euro-pean Journal of Operational Research,2009,192(3):929-948.
[9]张菊亮,陈剑.供应商管理库存应对突发事件[J].中国管理科学,2008,16(5):71-76.
[10]蒋宇,杨西龙,张巍.基于VMI和价格补贴机制的军事供应链协调模型[J].物流技术,2016,35(2):173-176.
[11]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2004:198-202.
[12]程菱,胡大伟.收益共享机制下的VMI供应链模型研究[J].物流技术,2012,31(2):129-132.
[13]蒋宇,杨西龙,张巍.军事供应链供应商管理库存应用研究[J].后勤工程学院学报,2015,31(5):46-50.
(责任编辑: 王生凤)
Supply Chain Revenue Sharing Coordination of Vehicle Equipment Based on VMI
WEN Zheng-zhong1, WANG Liang2, HE Jian1, ZHANG Da-peng2
(1. Brigade of Postgraduate Management, Academy of Military Transportation, Tianjin 300161, China;2. Department of Military Vehicles, Academy of Military Transportation, Tianjin 300161, China)
In order to reasonably allocate the gains of military supply chain system after the implementation of the Vendor Management Inventory (VMI) strategy, the coordination models with three kinds of revenue sharing mechanisms of the traditional, the Stackelberg game, the Nash equilibrium negotiation are built to coordinate VMI. And it carries on the example analysis, the result shows that the traditional VMI model is lack of rationality and operability, the Stackelberg game model can make both the military and the supplier’s own revenue has some improvement, but the overall profit of the supply chain cannot reach the maximum, the Nash equilibrium negotiation model can not only make the military and the supplier’s own revenue improved, achieve a win-win situation, but also to make the overall profit of the whole supply chain reach Pareto optimal.
Vendor Management Inventory (VMI); revenue sharing coordination; Stackelberg game; Nash equilibrium negotiation
1672-1497(2016)04-0024-06
2016-04-27
文正中(1992-),男,硕士研究生。
E92
A
10.3969/j.issn.1672-1497.2016.04.005

