3维编织复合材料弹道侵彻数值模拟结果的可靠性分析

宫　雷， 许世蒙， 杜建华

(1. 装甲兵工程学院基础部， 北京 100072； 2. 装甲兵工程学院科研部， 北京 100072)



3维编织复合材料弹道侵彻数值模拟结果的可靠性分析

宫雷1， 许世蒙1， 杜建华2

(1. 装甲兵工程学院基础部， 北京 100072； 2. 装甲兵工程学院科研部， 北京 100072)

为分析3维编织复合材料弹道侵彻数值模拟结果的可靠性，采用参数检验和非参数检验2种统计检验方法，对试验与2种数值模拟过程得到的剩余速度分布分别进行了齐一性检验，结果表明：非参数检验方法能准确检验数值模拟结果的可靠性；第2种数值模拟过程得到的剩余速度分布与试验结果分布相同,具有更高的可靠性。

可靠性分析； 配对样本t检验； Smirnov检验； 随机游程检验

数值模拟是3维编织复合材料弹道侵彻的主要研究方法之一[1-4]。人们在现代数学、力学理论的基础上，结合有限元、有限容积或有限差分等方法，将现代计算机技术、软件工具、算法和工程知识结合在一起，获得满足工程要求的数值解，通过数值计算和图像显示的方法，模拟3维编织复合材料的动态侵彻过程中弹体、靶体的变形及破坏形态，为进一步分析动态侵彻过程中材料的破坏机理，以及研究纤维和填充物间应力波传播方式奠定基础。

数值模拟结果的可靠性分析对研究3维编织复合材料的弹道侵彻机理、完善弹道侵彻的数学模型，从而更好地指导弹道侵彻试验具有重要的意义。目前，主要是通过人工识别的方法对比侵彻模拟图片与实际试验图片，或者采用方差、标准差和相对误差等统计量检验数值模拟与实测剩余速度的差异，进而分析数值模拟结果的可靠性[5]。这些方法操作简单，从一定程度上能够比较数值模拟与实测结果的差异，但对造成差异的系统误差和随机误差分辨不清，对数值模拟结果的可靠性分析不足。

笔者以试验结果为基础，采用参数检验和2类非参数检验方法，对试验与2种数值模拟过程中剩余速度的分布分别进行齐一性检验，即对比试验与数值模拟剩余速度的分布是否相同，进而区分系统误差与随机误差，检验数值模拟结果的可靠性。这种方法充分利用了数值模拟和试验数据以及其他辅助信息，检验可信度较高，为识别和选择检验方法提供了较大的灵活性。

1　弹道侵彻数值模拟过程

1.1数值模拟

3维编织复合材料动态侵彻数值模拟[5]过程的核心在于建立反映问题本质的数学模型并寻求高效准确的计算方法。本文中数值模拟的过程与实测数据密切相关，为了建立科学的3维编织复合材料的动态侵彻模型，需要将数值模拟结果与实测数据反复进行比较，在此基础上不断修改数学模型。本文采用LS-DYNA程序先后进行了2次数值模拟，其有限元计算过程如表1所示。

表1　3维编织复合材料动态侵彻的数值模拟有限元计算过程对比

1.2数值模拟结果与试验数据对比分析

数值模拟结果与试验数据需进行科学合理的对比分析才能更好地应用于实践。为了取得好的效果，数值模拟结果与试验数据需经过多次反复对比分析，先进行机理分析，然后进行数值模拟。将部分靶试结果与数值模拟结果进行比较分析，若二者结果不同，应及时修正模型或改进试验，完成后再进行数值模拟、靶试和对比分析。数值模拟结果与试验数据对比分析流程如图1所示。

2　可靠性分析方法

3维编织复合材料弹道侵彻的数值模拟可靠性可在获得可靠试验数据的基础上，通过比较数值模拟结果与试验数据的分布是否相同来进行判断。

对于检验问题(a)：

H0,数值模拟结果与试验数据分布一致；

H1,数值模拟结果与试验数据分布不一致。

可采用参数检验和非参数检验2种方法进行可靠性分析。

图1　数值模拟结果与试验数据对比分析流程

2.1参数检验方法

配对样本t检验[6]能够判断2个同质的样本分别接受2种不同的处理或一个样本先后接受不同的处理是否有差别。在3维编织复合材料数值模拟结果和试验数据中，可选取入射速度相同的样本点，此时数值模拟和试验剩余速度的差异可看成是仅由数据生成方式不同引起的，因此同一入射速度各对数据的比较能够排除其他因素，而只需考虑数据生成方式对剩余速度的影响，从而能够采用配对数据t检验来比较数值模拟结果与试验数据是否有显著差异。

设有n对相互独立的观察结果(X1,Y1),(X2,Y2),…,(Xn,Yn)，令D1=X1-Y1,D2=X2-Y2,…,Dn=Xn-Yn，则D1,D2,…,Dn相互独立。若原假设H0成立，可认为Di(i=1,2，…，n)仅是由随机因素引起的，因此D～N(0,σ2)，检验问题(a)转化成检验问题(b)：

H0， μD=0；

H1， μD≠0。

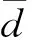
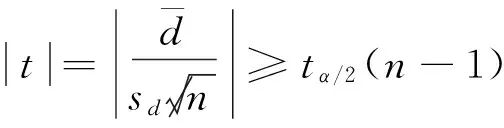
(1)

t检验局限于配对样本方差服从正态分布的情况，当数据偏离正态分布太多时，t检验就会失效，此时可考虑采用非参数检验方法。

2.2非参数检验方法

非参数检验方法对总体分布的假设较少，结果具有较好的鲁棒性，能够处理所有类型的数据，具有广泛的实用性。本文采用非参数检验方法中的Smirnov检验[7]和游程检验[8]对数值模拟结果与试验数据的一致性进行检验。

2.2.1Smirnov检验方法

Smirnov检验能够比较2个独立样本总体分布的异同，对2个样本经验分布函数的位置和形状参数的差异均敏感，是比较2个样本最常规且有效的非参数检验方法之一。

假设X1,X2,…,Xm～F(x)，Y1,Y2,…,Yn～G(x)且全样本独立，F(x)和G(x)为连续分布函数，检验问题(a)转化成检验问题(c)：

H0，F(x)=G(x)；

H1，F(x)≠G(x)。

Smirnov检验统计量：

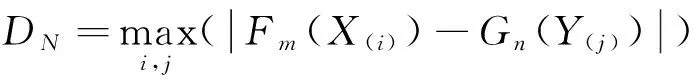
(2)

式中：X(i)、Y(j)分别为X、Y的顺序统计量。

Smirnov检验的步骤如下：

1)将2组样本按升序排列；

2)分别计算2组样本秩的累计频数和累计频率；

3)计算2组样本秩的累计频率的差，得到秩的差值序列及D统计量；

4)根据拒绝域得出结论。

2.2.2随机游程检验方法

随机游程检验亦称“连贯检验”，是根据样本标志表现排列所形成的游程的多少来判断2个样本分布异同的检验方法。

在一个二元0-1序列中，一个由0或1连续构成的串称为游程，一个游程中0或1的个数称为游程长度。游程个数反映了0和1交替轮换的频繁程度，通常用R表示。

在3维编织复合材料弹道侵彻的数值模拟结果与试验数据的一致性研究中，若检验问题(a)的原假设成立，将数值模拟结果与试验数据按升序排列后，2种结果出现顺序是随机的，检验问题(a)转化成检验问题(d)：

H0，2种结果出现顺序随机；

H1，2种结果出现顺序不随机。

若数值模拟结果和试验数据个数分别为m和n，给定水平α后，可以得到拒绝域为R≤r1或R≥r2, 临界值为

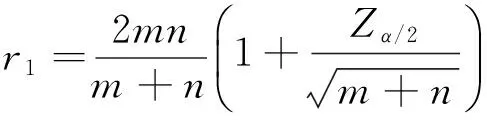
(3)

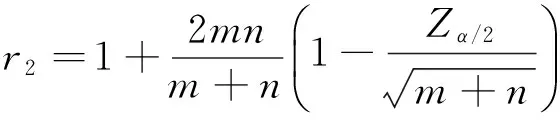
(4)

随机游程检验的步骤如下：

1)将2组样本混合后按升序排列；

2)计算游程；

3)计算统计量R；

4)根据拒绝域得出结论。

3　数值模拟结果的可靠性分析

3.1数值模拟与试验结果

试验[9-10]中采用荷兰Tarpon®1000型纤维材料、对位芳族聚酞胺纤维长丝束合股作为3维编织复合材料；采用热固性环氧树脂作为基体，纵横阵列编织机织造。采用56式弹道发射枪，7.62 mm步枪标准弹，共测试15组子弹的入射速度与剩余速度，结果如表2所示[7]。

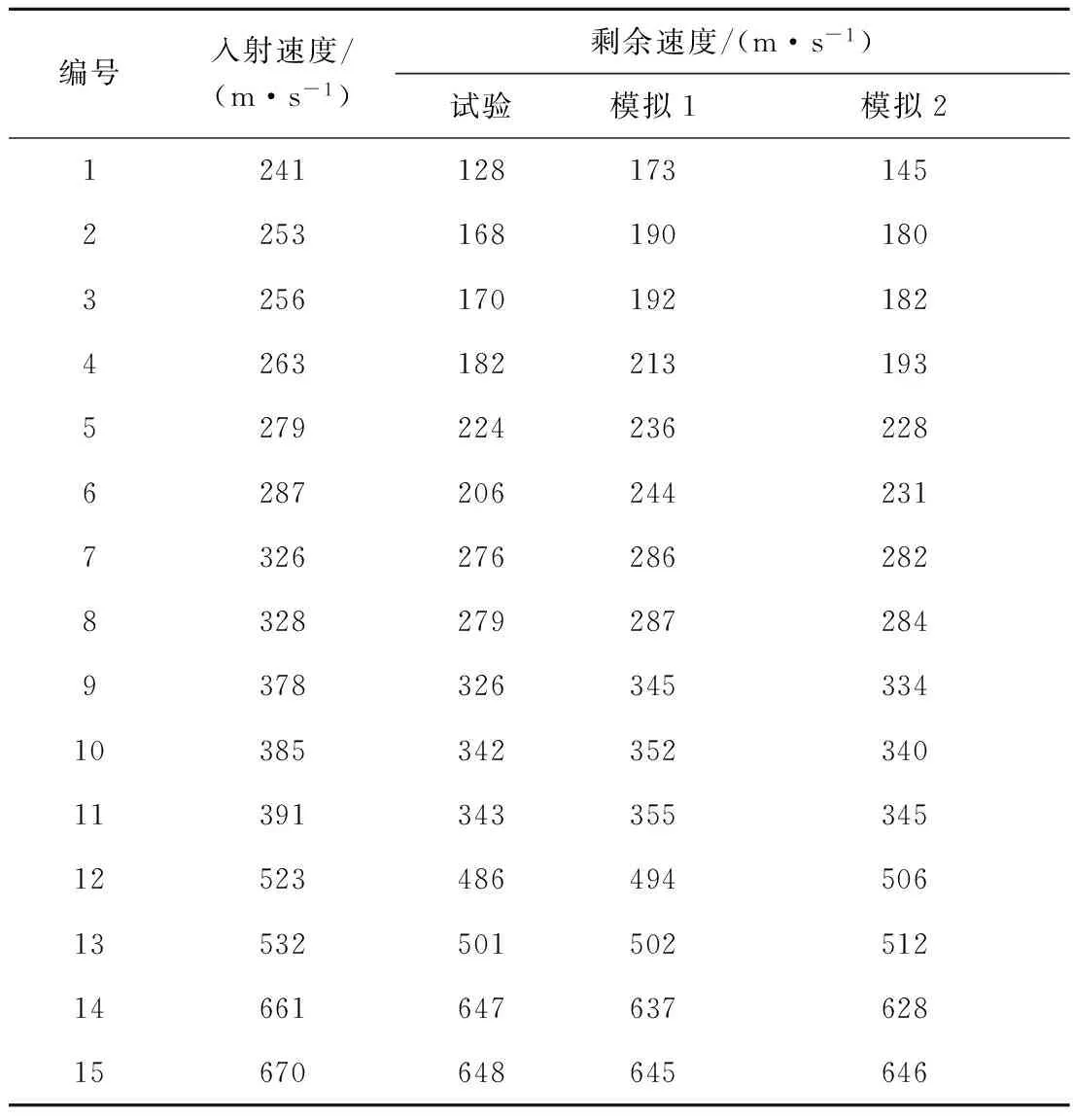
表2　3维编织复合材料弹道侵彻试验与数值模拟结果

3.2可靠性分析

为分析数值模拟结果的可靠性，首先将数值模拟结果与试验数据进行对比，如图2所示。

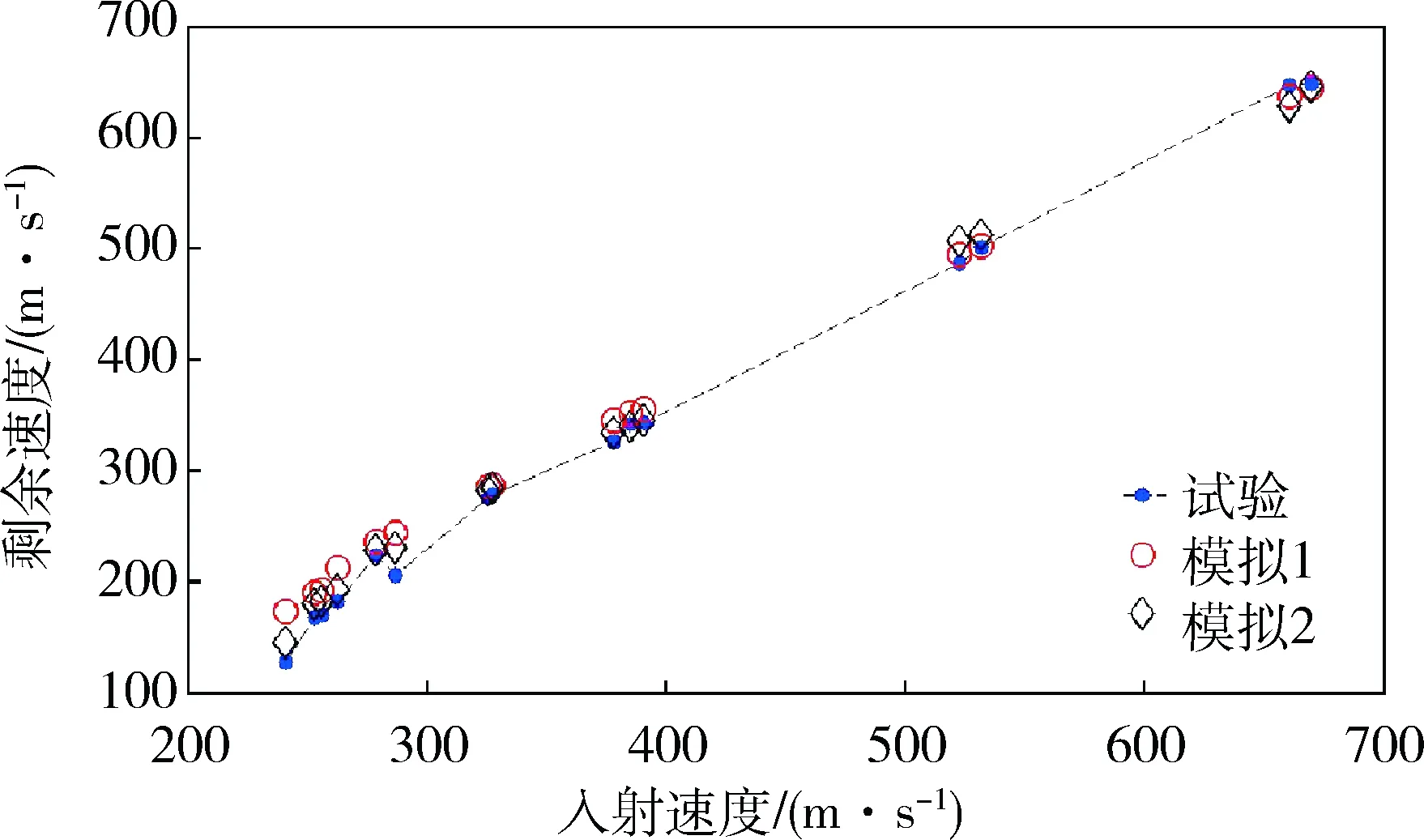
图2　数值模拟结果与试验数据对比

从图2可以看出：数值模拟1的剩余速度与试验数据存在一定差别，数值模拟2的剩余速度与试验数据基本一致。可进一步研究数值模拟结果与试验数据分布的异同，以判断数值模拟结果的可靠性。

3.2.1参数检验

对于检验问题(b)，在显著性水平α=0.05下，由于n=15，tα/2(14)=2.144 8，因此拒绝域为

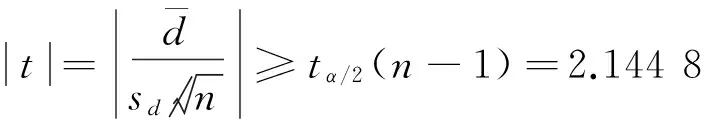
3.2.2非参数检验

影响剩余速度的主要因素为入射速度和数值模拟/试验方法的选取，由于实践中入射速度不同且差异巨大，因此其成为影响剩余速度的最主要因素。而本文主要目的是检验数值模拟结果的可靠性，即数值模拟结果与试验数据的对比分析，因此需先对试验中入射速度与剩余速度进行回归分析，得到剩余速度的残差，从而消除入射速度的影响，然后采用非参数检验方法进行可靠性分析。

通过试验结果分析可知：入射速度x与剩余速度y1具有明显线性关系[5]，可近似表示为

y1=1.153x-113.369。

(5)

由式(5)可得数值模拟和试验剩余速度的残差，如表3所示。

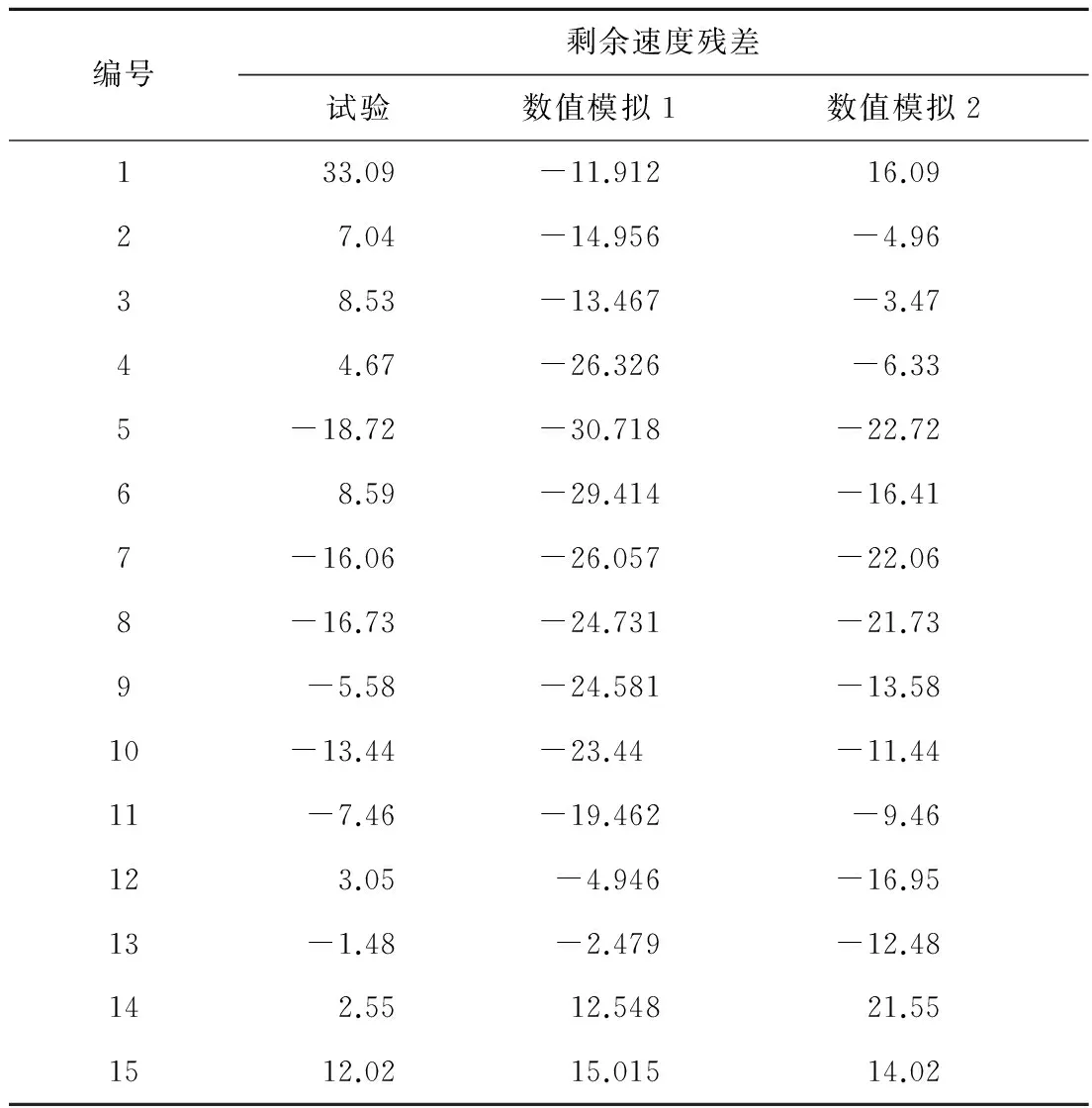
表3　数值模拟和试验剩余速度残差

令ε0(i)、ε1(j)、ε2(j)分别表示试验数据、数值模拟1结果、数值模拟2结果残差的顺序统计量， 0和1分别表示游程中的样本来自于试验数据和数值模拟结果，根据表2可得非参数检验结果，如表4所示。

1) Smirnov检验

试验数据与2次数值模拟结果的个数均为15，由表4可知：D1N=8/15，D2N=6/15。经查表[7]可知：

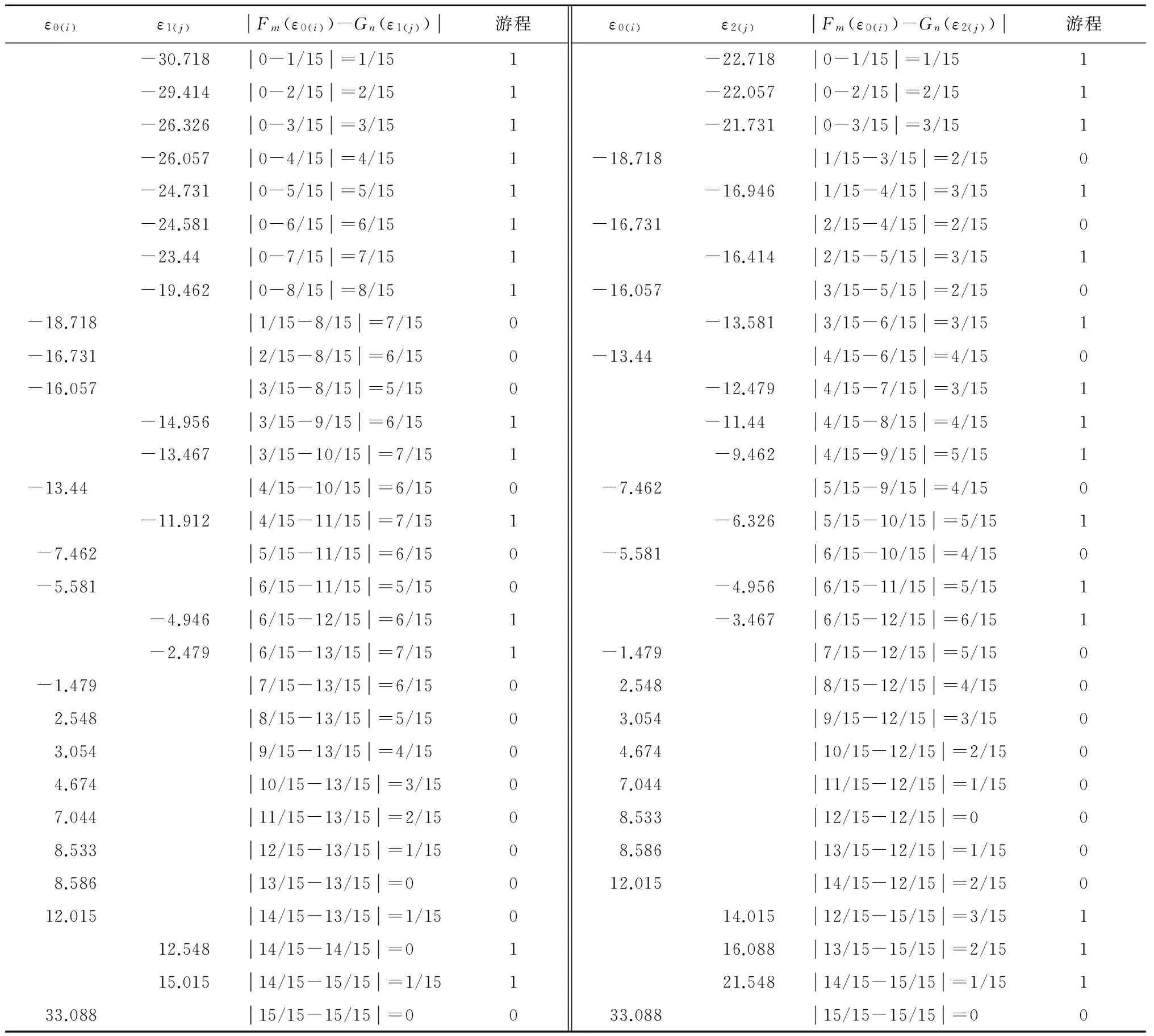
表4　非参数检验结果

在显著性水平α=0.05下，

PH0(D1N≤8/15)=0.98>1-α=0.95，

PH0(D2N≤6/15)=0.90<1-α=0.95。

可见：D1N在拒绝域内，D2N不在拒绝域内。

2) 随机游程检验

由表4可知：2次数值模拟结果与试验数据的游程个数分别为R1=10，R2=16。经查表[8]可知：在显著性水平α=0.05下，拒绝域的临界值r1=10，r2=22。可见：R1=r1，在拒绝域内；r1

由以上分析可知：采用 Smirnov检验和随机游程检验2种非参数检验方法进行数值模拟可靠性分析，得出数值模拟1结果与试验数据分布不同，具有显著差异，而数值模拟2结果与试验数据分布相同，不具有显著差异；采用参数检验方法进行数值模拟可靠性分析，得出2次数值模拟检验统计量均在拒绝域内，表明2次数值模拟结果与试验数据均具有差异，但数值模拟2结果的差异更小。

综合考虑参数检验和非参数检验结果，可认为：3维编织复合材料弹道侵彻数值模拟2结果与试验数据不存在较大差异，其分布相同；采用第2种数值模拟过程对3维编织复合材料的动态侵彻过程进行数值模拟可靠性较高。

4　结论

笔者将非参数检验方法引入到3维编织复合材料弹道侵彻数值模拟结果的可靠性分析中，通过分析数值模拟结果与试验数据的差异(即分布的异同)来检验可靠性。非参数检验需要的实测数据较少，检验成本较小，充分利用了数值模拟与试验数据信息，检验结论可信度较高，在方法上更具有先进性。本文的研究结果对定制新材料的科学分析，研究数值模拟方法的合理性，以及改进模型、调整试验内容和方法具有重要的理论意义和应用价值。

[1]Na W J, Ahn H C, Jean S Y. Prediction of the Braid Pattern on Arbitrary-shaped Mandrels Using the Minimum Path Condition[J]. Composites Science and Technology， 2014,91(4):30-37．

[2]徐静怡,顾伯洪. 三维编织复合材料弹道冲击破坏形态及破坏模式[J].弹道学报,2002,14(2):39-43.

[3]顾伯洪,徐静怡.三维编织复合材料弹道侵彻准细观层次有限元计算[J].复合材料学报，2004,21(3): 84-90.

[4]Gu B H, Xu J Y. Finite Element Calculation of 4-Step 3-Dimensional Braided Composite under Ballistic Perforation [J].Composites Part B, 2012,35 (4): 291-297.

[5]练军.三维编织复合材料弹道侵彻的数值模拟[D].上海：东华大学, 2006.

[6]王勤,刘晓莉,刘小娟.t检验在条干仪纱疵数据对比中的应用[J].上海纺织科技, 2013,41(10):30-31.

[7]吴喜之.非参数统计方法[M].北京：高等教育出版社, 2008:146-149.

[8]王星.非参数统计[M].北京：清华大学出版社, 2008:68-71.

[9]宫雷,许世蒙,杜建华,等. 3维编织复合材料弹道测试数据的异常点分析[J]. 装甲兵工程学院学报,2014,28(5):94-97.

[10]宫雷,许世蒙,杜建华,等. 基于双层Bayes分析的3维编织复合材料弹道侵彻异常点检验[J]. 装甲兵工程学院学报,2015,29(4):107-110.

(责任编辑: 尚彩娟)

Reliability Analysis of Numerical Simulation Results of 3D Braided Composite’s Ballistic Penetration

GONG Lei1, XU Shi-meng1, DU Jian-hua2

(1. Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China;2. Department of Science Research, Academy of Armored Force Engineering, Beijing 100072, China)

In order to analyze the reliability of numerical simulation results of the 3D braided composite’s ballistic penetration, this paper uses two statistical test methods such as parametric test and nonparametric test to take the homogeneity test for the residual velocity distributions of the two numerical simulation results and the real testing result. The analysis conclusions show that: the nonparametric method is effective to test the reliability of the simulation result; the second simulation result has the same residual velocity distribution with the real testing result, which is more reliable than the first.

reliability analysis; pared-samplesttest; Smirnov test; random run-length test

1672-1497(2016)04-0105-06

2016-05-23

国家自然科学基金资助项目(51001117)；北京市自然科学基金资助项目(3132024)

宫雷(1980-)，男，讲师，硕士。

TB114.3

A

10.3969/j.issn.1672-1497.2016.04.021