音圈电机驱动小角度转台控制方法研究
邵琳达,赵英伟
(1.中南大学 信息科学与工程学院,长沙 410012;2.国防科学技术大学 光电科学与工程学院,长沙 410073)
音圈电机驱动小角度转台控制方法研究
邵琳达1,赵英伟2
(1.中南大学 信息科学与工程学院,长沙410012;2.国防科学技术大学 光电科学与工程学院,长沙410073)
设计了基于相关辨识原理的频率特性测试仪,确定了音圈电机驱动小角度转台的传递函数,辨识出转台中存在的机械谐振环节,设计了相关的补偿环节,改善了转台的相位裕度,消除了中低频段机械谐振的影响。实验结果表明,实验采用的系统辨识方法在中低频段有较高的辨识拟合精度,辨识精度优于0.5 dB;根据辨识传递函数设计的补偿环节,可以使转台的控制角度定位精度达到2″,能够满足高精度的定位需求并具有较强的抗干扰能力。
小角度转台;音圈电机;系统辨识;频率补偿
本文引用格式:邵琳达,赵英伟.音圈电机驱动小角度转台控制方法研究[J].兵器装备工程学报,2016(8):142-145.
音圈电机是一种基于安培力原理制造的电磁力驱动直线运动电机[1-2]。它与其他直线驱动方式相比,具有行程大、体积小、驱动电压低、运动精度高的优点[3]。音圈电机已经广泛应用于各种系统:文献[4]中将音圈电机用于X-Y精密定位平台,其定位精度可以达到1 μm。文献[5]中将音圈电机用于航空相机相面扫描系统,采用音圈电机持续力控制和滞后超前控制相结合的控制策略满足工程应用需求。文献[6]中把音圈电机用于双层主动隔振系统,其隔振效果与被动隔振相比有了较大的提升。音圈电机在调焦系统中也有广泛应用[2]。
音圈电机在响应下具有复杂迟滞特性[7],增加了控制的难度,其主要的控制方法主要包括PID控制方法和经典的频域补偿方法。但是,传统的PID控制方法,参数整定难,抗干扰能力差,不能实时控制。因此,一些改进的PID控制方法在音圈电机控制系统中得到了较大的发展:文献[8]提出了模糊PID控制策略,提高了系统的鲁棒性及自适应性。文献[9]设计的神经网络PID控制策略利用神经网络的在线学习功能,提高了音圈电机直驱阀的自适应能力。文献[10]设计了模糊非线性PID控制,使系统具有很强的抗干扰能力。文献[11]用不完全微分PID控制方法对用旋转音圈电机驱动的二位快速水冷反射镜装置进行控制,在高精度光栅编码器反馈下,其稳定精度可以达到1″。这些方法在一定程度上对传统PID控制方法进行了改进,但是普遍存在计算量大,控制策略难以实现,无法满足实际应用要求。因此,经典的频域补偿方法在音圈电机系统中仍发挥着巨大的作用。而当被辨识对象传递函数不容易获得时,经典频域补偿方法就退化为PID控制[12]。
本文设计了一种音圈电机驱动、测角装置反馈的小角度转台;根据相关辨识原理,利用LabVIEW编程实现虚拟频率特性测试仪,并用该测试仪对转台的频率特性进行测试;采用MATLAB的curve fit工具箱对测得数据进行拟合,得到了系统的传递函数,设计了相关的补偿环节并给出了测试结果。实验证明,该方法角度定位精度较高,抗干扰能力较强。使用的系统辨识方法设计简单、方便快捷,辨识效果明显。
1 音圈电机驱动小角度转台结构设计
小角度转台结构示意图如图1,转台台面通过弹性支撑与基座相连,两个音圈电机分别安装在弹性支撑两端等距离位置。当电机中有电流流过时,两个电机向相反方向运动,从而驱动转台产生一定程度的倾角[13]。
图1中测角装置的测角精度优于2″,用于反馈转台的偏转角度。从转台的结构可以看出,该小角度转台为一个单自由度的扭振系统,音圈电机的电气部分相当于一个L-R网络。根据机械平衡方程和电势平衡方程,可以推导出转台的传递函数如下式
(1)
其中
DEN = (mL2s2/2 + 2mcL2s2+ 2CL2s + 2KL2)·
式(1)中:K为电机与弹性支撑的合成刚度;C为等效阻尼系数;L为驱动器作用点到转轴的距离;mc为音圈质量;m为台面质量;Lm和R是音圈电机的电感和电阻;Bgl是音圈电机的力常数。
由于三阶多项式总存在一个实数根,因此转台的传递函数可以分解为一个惯性环节和一个二阶振荡环节的串联,即
(2)
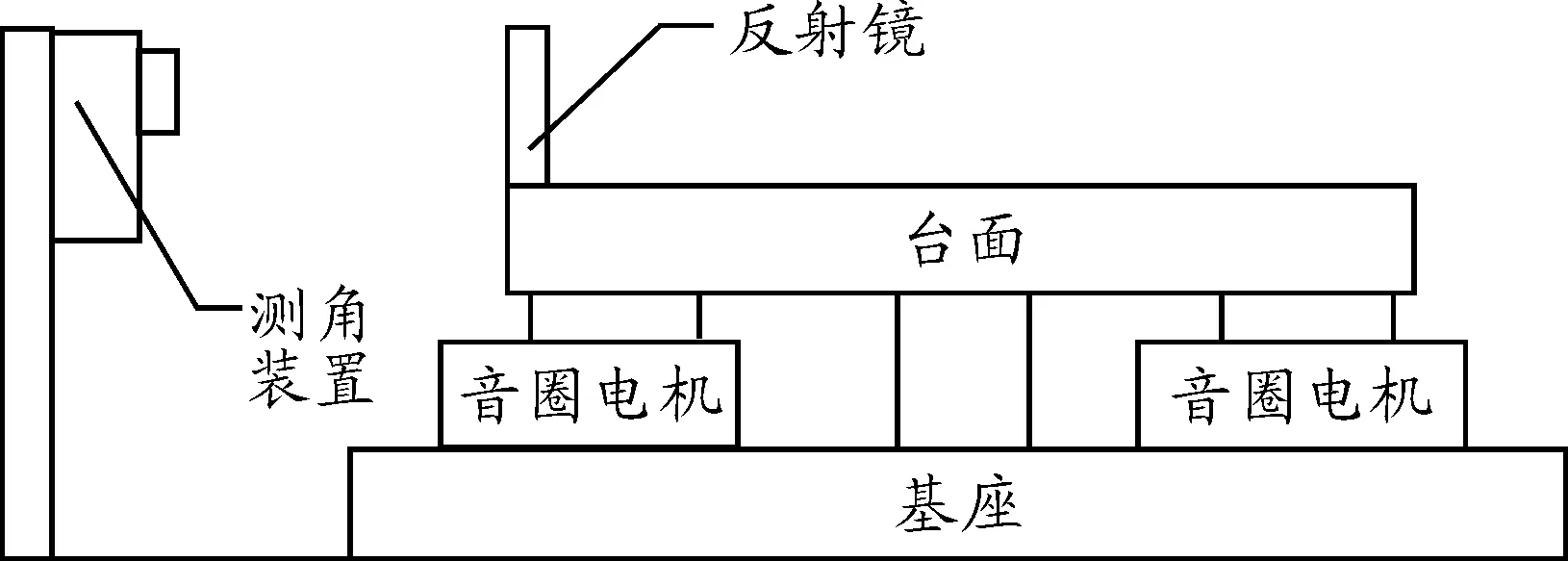
图1 音圈电机驱动小角度转台结构示意图
2 转台传递函数辨识
确定转台准确的传递函数是从频域角度对系统进行设计补偿的基础。文献[14]采用自适应卡尔曼滤波的方法辨识伺服系统的传递函数。相关辨识法、时域辨识法、扫频法等方法也广泛用于确定系统的传递函数。扫频法是通过向被测系统输入一系列频率可变的正弦信号,通过记录输入输出正弦波信号的幅度和相位的差异确定系统的传递函数特性。扫频法耗时较长且在扫频过程中要根据系统的特性实时调整输入信号的幅度大小,以防出现输入信号幅值过小响应信号被噪声淹没或者幅度过大使系统饱和的现象。这使得扫频法的辨识过程变得较为复杂。时域辨识法是通过向被测系统输入一个阶跃信号或者伪随机信号并记录系统的输出信号,通过最小二乘拟合系统的传递函数。由于在辨识前无法充分估计系统传递函数的特性及其中所包含的各个环节,在系统频率特性未知的情况下,时域辨识法只能获得系统的主传递函数而无法对系统中包含的双二阶机械谐振环节等做出准确的估计,这是时域法的最大缺陷。本文所用的相关辨识法采用通过向系统中输入高斯白噪声,计算系统输入信号x[n]的能量密度谱Sxx(ejω),以及输入信号x[n]和输出信号y[n]的互能量密度谱Syx(ejω),并采用将得到的Syx(ejω)、Sxx(ejω)进行相除的相关辨识法确定系统的传递函数。相关辨识法耗时短,对系统噪声有较强的抑制能力;该方法获得的频率数据点数和频率范围可通过采样频率和采样点数确定。辨识过程更加灵活,获取的信息量也更大,可以用测得的数据充分估计系统中存在的各个环节的特性。相关辨识法的测量原理如下:
转台可以视为线性时不变系统,其输入输出关系满足:

(3)
设输入信号的自相关序列为rxx[l],互相关序列为ryx[l],则上式可化为:
(4)
在z域中,上式等价于Syx(z)=H(z)Sxx(z),其中Sxx(z)和Syx(z)分别是rxx[l]和ryx[l]的z变换,H(z)是转台的传递函数。在单位圆上,有
(5)
转台系统的频率响应函数为
(6)
基于上述原理,利用LabVIEW设计一个虚拟频率特性测试仪,其主要实现向转台输入高斯白噪声,采集测角装置的输出信号,以及进行相关运算。实验测得的系统幅频特性曲线如图2所示。

图2 小角度转台幅频特性
从图2中可以看出,系统在1 897.522 rad/s和2 680.28 rad/s处有两个机械谐振环节,系统的传递函数可以写为
(7)
其中,G1(s)、G2(s)的形式如式所示
(8)
利用Matlab的Curve Fit功能,对机械谐振环节和系统低频段的特性分别进行辨识[15],得到系统的传递函数如式(9)所示
(9)
辨识出的传递函数波特图如图3所示。从图3中可以看出,系统的传递函数在中低频段拟合效果较好,反映了系统的特性,拟合精度小于0.5 dB。在高频段拟合效果较差,其原因是在高频段,系统的非线性非常显著,频率特性中含有多个小的谐振环节,而传递函数并未对其进行处理。另外,由于测角装置噪声的影响,测得的幅频特性曲线有一定程度的“毛刺”。而“毛刺”的幅值较小,辨识过程中可以将其忽略。

图3 小角度转台幅频特性辨识结果
3 补偿环节设计
根据辨识得到的系统传递函数的特性,将其分为两大部分:主传递函数G0(s)和机械谐振环节G1(s)、G2(s)。两个机械谐振环节的存在会降低主传递函数的相位裕度,增加补偿环节的设计难度,因此从频率角度设计传递函数的串联补偿环节时,除了需要考虑如何提高主传递函数的相位裕度,还应对两个机械谐振环节进行处理。
通过串联滞后补偿环节,降低系统的截止频率来提高主传递函数的相位裕度,具体的参数可以根据系统的具体要求来设置。机械谐振环节可以通过串联双T网络消除,但是,双T网络在谐振点的大幅度衰减造成了系统幅频特性在谐振点附近的严重非线性,影响系统的动态性能。本文采用的辨识方法可以对机械谐振环节进行较为精确的辨识,因此,可以采用直接串联机械谐振倒数的方式抵消谐振环节对系统频率特性的影响来消除机械谐振环节的影响。直接对消的方法可以保证系统的闭环带宽和稳定裕度不至于受到太大的影响。综上所述设计如下所示的补偿环节
(10)
式(10)中,第一项为滞后补偿环节用以提高系统的相位裕度,第二项、第三项用来抵消系统中的机械谐振环节,最后一项用来改善系统主传递函数在谐振峰位置的幅频特性。加入补偿环节后,系统开环传递函数的波特图如图4所示。
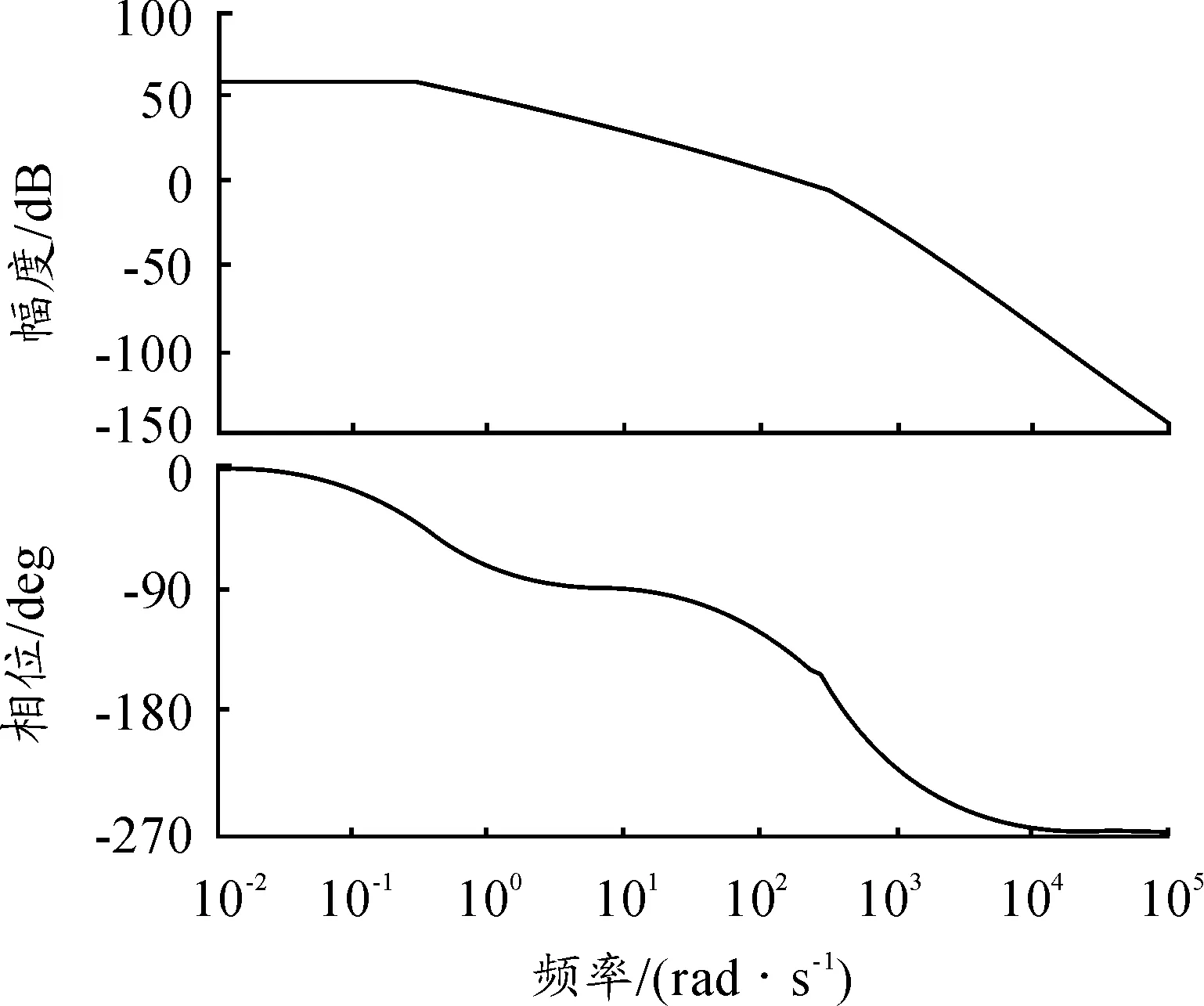
图4 补偿后的波特图
从图4可以看出,加入补偿环节后,系统的相位裕度有了显著提高,双二阶机械谐振环节已经被消除,系统的相位裕度提高到45°。
4 实验结果
为进一步验证系统传递函数辨识方法以及设计补偿环节的有效性,设计了如图5所示实验装置。由于小角度转台传递函数中机械谐振环节的存在,PID控制方法的参数调节比较复杂,难以找到理想的控制参数。因此,实验中并未用PID方法与频率设计法进行比较。
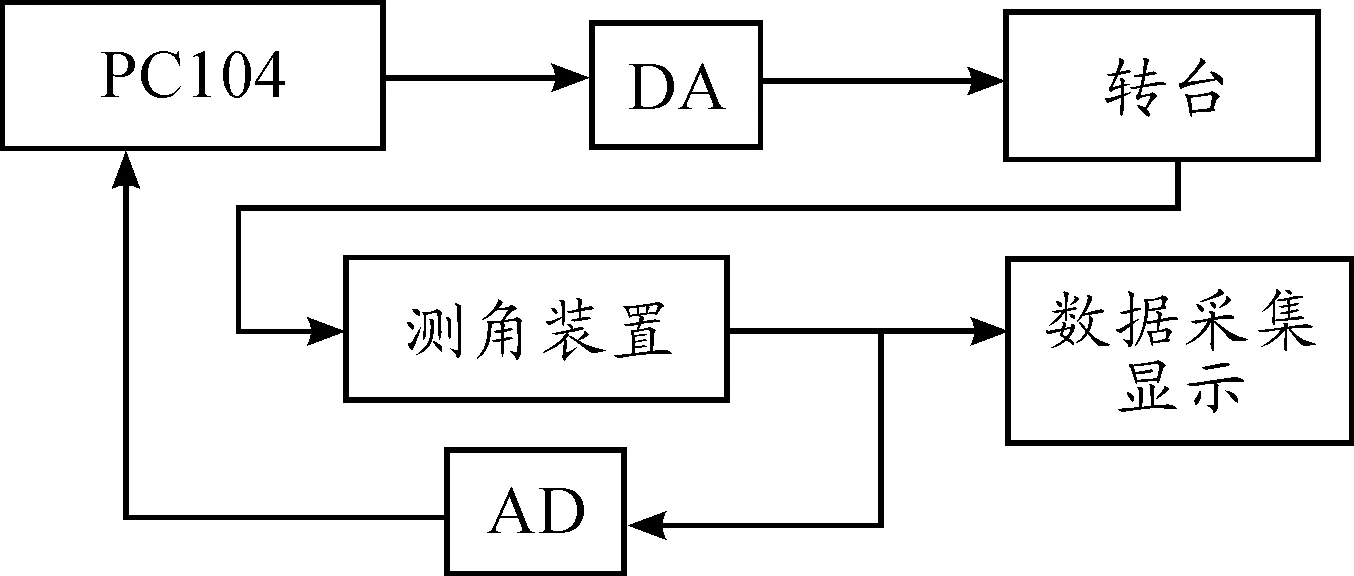
图5 实验装置示意图
图5中,AD、DA的位数分别为16位和12位。数据采集显示工具为LabVIEW以及DAQ数据采集卡编程实现的虚拟示波器,便于图形的截取以及数据保存。
通过PC104向转台输入一个180″的阶跃信号,转台转过的角度变化曲线如图6所示。从图6可以看出,输入阶跃信号后,转台在初始阶段有一个40″超调量,然后迅速稳定到180″的位置。不考虑测角装置噪声的影响,转台稳定精度可达2″。系统的输出结果证明了文中用到的系统辨识方法以及所设计控制环节的准确性。
为检验转台的抗干扰能力,在某些时刻向转台施加一系列的干扰信号,转台的转过角度如图7所示。从图7可以看出,加入干扰力后,转台会偏离稳定状态时的角度位置。当干扰力撤销后,转台会迅速恢复稳定状态。这说明转台的抗干扰能力较强,可以抵抗一般的外界干扰。
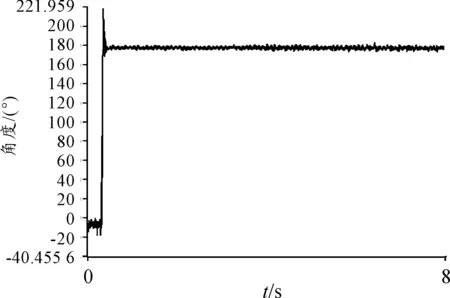
图6 实验结果

图7 转台加干扰后的定位效果
5 结论
本文给出了音圈电机驱动的小角度转台的结构形式,采用白噪声信号作为音圈电机驱动小角度转台的系统辨识输入信号,用相关辨识法准确地辨识转台的传递函数,在中低频段的辨识拟合精度小于0.5 dB。结合转台传递函数的特点设计了相关的频率补偿环节,解决了机械谐振环节对转台性能的影响,提高了转台的相位裕度。仿真以及实验结果表明,该转台的角度控制定位精度达到2″,并且有较强的抗干扰能力,基于LabVIEW的系统辨识方法结构简单,操作方便,对系统补偿具有较高的指导意义。
[1]曹水亮,杨志军,陈新度.基于电磁场仿真的音圈电机建模与设计研究[J].微电机,2013,46(10):13-19.
[2]马建设,张莹.调焦用微型音圈电机磁场仿真及关键参数分析[J].微电机,2014,47(3):1-4.
[3]冯晓梅,李立顺,李红勋,等.直线音圈电机特性研究[J].微特电机,2014,42(12):38-48.
[4]冷同同,靳东,刘博峰.基于音圈电机X-Y精密定位平台的控制系统设计[J].组合机床与自动化加工技术,2013(9):73-76.
[5]杨守旺,万秋华,孙莹,等.音圈电机驱动的航空相机像面扫描系统[J].红外与激光工程,2014,43(5):1540-1544.
[6]陈照波,吕俊超,焦映厚.音圈电机驱动的双层主动隔振系统设计与仿真[J].噪声与振动控制,2012 (5):26-30.
[7]党选举,王占军,杨大磊.高频响应下音圈电机复杂迟滞特性建模与验证[J].振动与冲击,2012,31(9):107-112.
[8]刘日龙,殷德奎.音圈电机伺服系统模糊PID控制[J].微特电机,2010(7):63-68.
[9]张立强,陈强,柳志姣,等.音圈电机直驱阀的神经网络PID控制[J].液压与气动,2015(6):80-83.
[10]王大彧,郭宏,刘治,等.直驱阀用音圈电机的模糊非线性PID控制[J].电工技术学报,2011,26(3):52-56.
[11]邵帅,高云国,郭劲,等.二维快速控制水冷反射镜装置设计[J].光学精密工程,2009,17(3):493-498.
[12]钱富才,黄姣茹,秦新强.基于鲁棒优化的系统辨识算法研究[J].自动化学报,2014,40(5):988-993.
[13]徐新行,王兵,庄昕宇,等.音圈电机驱动型快速控制反射镜机械结构研究[J].长春理工大学学报:自然科学版,2011,34(1):49-52.
[14]魏彤,郭蕊.自适应卡尔曼滤波在无刷直流电机系统辨识中的应用[J].光学精密工程,2012,20(10):2308-2314.
[15]陈岚峰,张亚琴,程立英,等.基于数据的MATLAB系统辨识工具箱模型识别[J].沈阳师范大学学报:自然科学版,2013,31(4):527-530.
(责任编辑杨继森)
Research on Control Strategy of Voice Coil Motor Actuating Small-Angle Turntable
SHAO Lin-da1, ZHAO Ying-wei2
(1.School of Information Science and Engineering, Central South University,Changsha 410012, China; 2.College of OptoElectronic Science and Engineering,National University of Defense Technology, Changsha 410073, China)
A frequency characteristic analyzer of the small-angle turntable actuated by the voice coil motor (VCM) was designed based on the correlation system identification principle. Then, the table transfer function was identified, while the mechanical resonance parts were estimated. At last, the relevant compensator was designed, which was used to improve the phase margin of the table and eliminate the effects of the mechanical resonance parts. It is found from the experiment that this system identification method can reach a relatively high identification precision, which is 0.5dB in the lower and middle frequency domain. The frequency domain compensation method is with an accuracy of 2”, which can meet the requirement of high-accuracy angle positioning and stronger disturbance immunity.
small-angle turntable; voice coil motor; system identification; frequency domain compensator
2016-03-20;
2016-04-09
重力异常补偿机理及重力辅助导航技术研究(61275002)
邵琳达,女,主要从事信号与信息处理、电气工程及其自动化研究;赵英伟(1985—),男,讲师,博士,主要从事信号与信息处理、光电仪器与测控技术研究。
10.11809/scbgxb2016.08.032
format:SHAO Lin-da, ZHAO Ying-wei.Research on Control Strategy of Voice Coil Motor Actuating Small-Angle Turntable[J].Journal of Ordnance Equipment Engineering,2016(8):142-145.
TN302
A
2096-2304(2016)08-0142-05
【信息科学与控制工程】

