一种基于喷泉码的本地数据存储备份的方案

詹首道，龚洪波（广东工业大学计算机学院，广州　510006）

一种基于喷泉码的本地数据存储备份的方案

詹首道，龚洪波
（广东工业大学计算机学院，广州510006）

提出一种基于喷泉码、网络编码思想的数据备份方案。该方案基于喷泉码、网络编码的思想，并且具有纠删码的特性。在文件存储时，将文件块进行编码，产生很多编码块，对原始文件块和编码块进行挑选存储，最后进行存储的是原始块与编码块的混合，这样文件存储空间会变大。数据读取时，只需经过简单编码计算即可，一般都是线性运算。该方案利用空间和计算资源来换取数据的可靠性，在某种应用场景下有更好的鲁棒性。

喷泉码；网络编码；备份；鲁棒性

国家自然科学基金项目（No.61272013）、广东省现代信息服务业发展专项资金项目（No.GDEID2011IS022）、广东省省部产学研合作专项资金项目（No.2013B090500007）

0　引言

随着信息技术，尤其是人工智能、云计算的进一步发展，人们需要捕捉、管理和处理的数据正在以GB、TB甚至是PB为单位进行更新。越是庞大的数据计算，就需要越庞大的数据量。同时，存储设备的发展同样日新月异，大数据的爆发性增长也有了合适的存储环境，高可靠性成为人们存储技术的研究重点。数据的高可靠性变得更加重要，数据备份与恢复则是数据高可靠性的重要保证。

因为操作失误、软件故障、病毒、自然灾害等［1］造成的数据丢失、损坏，每天都在发生。不同的用户，会选择的备份还原方案各不相同。而不同的备份方案会有不同的备份效率。数据备份与恢复是相辅相成的，数据备份的方案决定了数据恢复操作的效率与执行。

现在的技术，采用最多的备份还原技术是数据复制［2］和镜像技术。数据复制最简单，将文件直接在另一个存储设备上复制一份，需要恢复时，直接读取，操作便利。事实上，会存在一种情况就是备份是文件已经出现损坏，这样同一数据块就同时出错，特别对于用于归档数据或用于容错容灾的目的情形［3］，更为突出。

考虑以下情景，存储一个文件，这个文件很重要，但是并不是马上使用，可能在几年内都不会使用。但是，在需要使用时，发现文件出现了损坏。在恢复还原时，发现备份的文件的也同样出现损坏。为了保证文件可以正常读取，最简单的方法就是在更多的设备上进行备份，而这种方法需要耗费更多的空间资源，问题却依然存在。本文提出了一种基于喷泉码与网络编码思想的数据备份技术，通过增加读取计算和空间存储，可以允许丢失部分数据，也能有效地读取原文件。

1　理论基础

时间复杂度、空间复杂度一直是算法和解决方案的优劣指标。然而，在某些情况下，空间比运算重要，有时却相反。这样就出现了以牺牲计算资源换取空间资源、提高效率的技术，如分布式存储系统通过计算编码提高了系统的性能；网络编码利用了中间结点的计算编码提高了网络的吞吐量等。下面简要介绍与本文相关的技术理论。

1.1分布式存储系统

分布式存储系统将数据分散存储在多台独立的设备上，利用分散在网络上大量节点的协作实现可靠的数据存储［5］。分布式存储技术的主要目的是通过使用一些分布式的存储节点（例如硬盘、无线传感器节点和P2P网络中的节点等）来长期地可靠地保存数据对象［6］。分布式存储的特点有：1）高可靠性；2）高性能；3）访问灵活；4）低成本。但同时主要有下面几方面不足：1）还不完善的软件体系；2）读取的稳定性不够；3）安全问题［5-6］。

1.2网络编码

在2000年由Yeung等发表的网络编码（Network Coding）［4］脱离了传统网络只能在中间节点存储转发的模式，提出了中间节点编码计算的新模式。通过网络编码技术，提高带宽的利用率，实现网络吞吐的最大化。到了2003年，线性网络中的网络编码的可行性［7］也被Yeung等人证明可行性。进一步研究发现，网络编码不单单能提高带宽的利用率、吞吐量，均衡流量，还可以提高网络的可靠性和安全性等［4，7］。

1.3喷泉码

数字喷泉技术［8］最早是由Luby等于1998年提出。目前的喷泉码有Reed Solomon编码［9］、Luby Transform编码［10］和Raptor编码［11］等。

喷泉码利用编码计算，提高用户接收文件的效率。目前的应用环境都与网络相关，与本地文件的读取无关。受到喷泉码的启发，本文结合网络编码将这种编码思想应用在存储备份中，将需要存储的数据进行编码，并增加的额外存储空间，提高文件的可靠性。

1.4纠删码

目前针对数据恢复使用比较多的技术是纠删码。这个技术是利用原有数据，通过简单编码，增加少量数据冗余来实现数据恢复。当前的纠删码，有不同的冗余生成方案，其容错能力、效率不一样，如容1错（RAID-5码），容 2错（EVENODD码［12］，X码［13］等），容多错（STAR码［14］，WEAVER码［15］以及Cauchy Reed Solomon码［16］等）。最近，文献［17］提出了4种关于纠删码的新方案。这些方案的核心是通过编码，增加数据冗余，提高数据的稳定性。

下文简单介绍容2错的EVENODD码和容多错的STAR码。

EVENODD码，是第一种提出的容二错阵列码，也是一种常见的阵列码，其编码是基于一个大小为（p-1）×（p+2）的阵列（P为素数）。阵列中存放原始数据的是前P列；增加了两列存放冗余校验数据做为校验列。（0≤i≤p-2，0≤j≤p+1）用于表示磁盘j中的第i块数据。将第p列，也就是两列校验列中的第一列称为行校验列，由第i行所有原始数据块进行异或得到对应的作为该列的校验块；最后一列称为对角线校验列，将调节因子s于对应对角线上所有原始数据块进行异或得到对应的，作为对角线校验列的校验块。

因为EVENODD码在编码、解码操作时使用简单的异或操作，所以计算复杂度比较低。

STAR可以说是EVENODD码的扩展，从容二错扩展到容三错，在EVENODD码的水平校验，对角线校验的基础上，增加了一个辅助对角线校验，增加了一个校验位，使得容错能力提高了一位。其编码是基于一个（p-1）×（p+2）阵列，符号（0≤i≤p-2，0≤j≤p+1）用于表示磁盘j中的第i块数据。前P块盘存放数据信息，第p、p+1个盘存放的与EVENODD码存放的一样，都是行校验与对角线校验，区别在于第p+2个盘存放的是辅助对角线校验位。

STAR码是在EVENODD码的基础上增加了第三个校验位辅助对角线校验，EVENODD码的特点STAR码也有，由于多了一个校验位，容错能力从容二错增强到了容三错。

目前，除了纠删码技术是处理本地数据的，其他技术针对的都是网络在线数据，基本没有涉及到本地数据，本文主要利用编码技术提高本地备份数据的可靠性。

2　优化编码存储规则

2.1编码规则

本文方案中，存储的文件块并不是所有原始块与编码规则相同的编码块，而是存储部分原始块与部分编码块，其中关于编码块的规则是任意k个原始块组合成一个编码块，这里的k＜=n（n为原始块数目）。在这个方案中，本文存储的文件大小会比原始文件稍大，但是相对一个方案来讲，存储的大小会大幅减少。

关于存储多少个原始块，多少个编码块，本文会在下面进行研究。为了方便研究，本文将对文件进行分4块，分别以a、b、c、d表示，其中，可以组成的编码块有ab、ac、ad、bc、bd、cd、abc、abc、acd、bcd、abcd，实际存储的块将在这15个块中选取。

这种方案的主要过程是∶文件存储前，先把文件分块，之后把所有可能的组合列出来，总共有s=种组合（k为分块数），然后从s个组合中随机挑选m（k＜m＜s）个，进行存储，这m个文件块不要求一定要有原始块或者要编码块，只需要数目达到要求。文件读取时，先判断原始块是否足够，若足够，则直接读取，若不足够，则利用已有的编码块与原始块进行解码，还原出原文件。

本文做了个简单程序去验证这分块编码存储的可靠性。

在这个程序的算法中，利用二进制运算的特性，可以模拟编码解码过程，具体过程如下：

（1）创建4个数组分别代表A、B、C、D，其中A［0 0 0 1］，B［0 0 1 0］，C［0 1 0 0］，D［1 0 0 0］；

（2）根据选取的文件块所包含的原始块信息，生成对应的数组，如有”AB”这个文件块，则用str1［1 0 0 1］表示，总共可以得到7个数组str1～str7；

（3）从得到的7个数组中挑选4，组合成一个4×4的矩阵，通过判定该矩阵是否有解，就可以知道该文件块组合能否还原文件；

（4）重复步骤（3），直到文件得到还原后或者所有文件块组合都尝试了，但文件无法还原才结束。

通过模拟程序的运行结果可以发现，将文件分成4块，通过编码增加了11块，再从15块中取7块文件进行文件还原是存在问题的，虽然绝大部分都可以还原，但是仍然有少部分组合是无法还原的。

这种编码方法，每个原始文件块分别存储在8个不同的块中，也就是说有7个块不包含这个原始文件块的信息，这种情况下，若取的块都是这7个块，如a，b，c，ab，bc，ac，abc，则说明这个原始文件块“d”的信息丢失了，无法还原出原始文件。

针对这种情况本文的方法是从15个块中取8个，就可以完全避免这个情况了。

在存储了8个块之后，本文进一步尝试，允许丢失块，在存储的过程中需要进行挑选编码块，而不是任意的8个块。挑选的规则主要是存储的块必须包含有所有原始文件块信息，而且不是单纯的任意块，而是每个原始文件块的信息都必须存在于若干个文件块中，如存储的块有b，ac，ad，bc，abc，abd，acd，bcd，在这种情况下包含“a”的信息块有5个，包含“b”的信息块有5个，包含“c”的信息块有4个，包含“d”的信息块有4个，每个原始信息的存在数目基本一致，且不小于文件分份数。完成存储后，根据包含的文件块信息最少的块的数目，决定允许丢失的数目。

2.2数据分析

本文中，将文件分成n块，可以组成2n-1个块，每个原始信息块存在的数目是（2n-1）-（2n-1-1）=2n-1个，所以每次存储的数目为2n-1+1个块，可以保证每个原始信息都被保存。但是如下图所示，如果n的值超过4，存储文件的大小将远远大于原文件，这样效率会变得十分低。

图1　文件分块数与编码数增长关系图

根据本文方案，确保了原始文件信息的可靠性，使得需要存储的块数明显降低。还有一点是容错能力变成可控的，不是固定的容x错（x为常数）。容错能力根据存储的文件块中的原始信息数而变。

容错分析：通过编码理论可以知道，最大距离可分码，也就是MDS码，存储效率是最高的，本文的方案不是MDS码，考虑的第一优先的不是效率，而是可靠性，但是就效率而言，并不比简单的容一错、容二错的编码低，而且可靠性更强。根据本文的编码存储规则，我们很容易就可以得到整个方案的存储效率E。

其中n为文件分块数，m为实际存储的文件块数，m随着n的不同而不同，且m≥n，容错能力为V=mn。

下图为编码过程中所有文件块的组合生成示意图，每一个节点向上遍历（只能向上）到第二层结束，这样就得到了一个编码块。如从第三层第四个元素“c”开始，往上读取“a”，到这里结束，就得到一个编码块”ac“，如从第五层第一个元素“d”开始，往上读取“c”、”b”、”a”，到这里结束，就得到一个编码块”abcd“，如从第三层第六个元素“d”开始，往上读取“c”，到这里结束，就得到一个编码块”cd“。当所有节点都读取过后，原始文件块所组成的编码块就全部组合完成。可以清楚地知道，生成编码块的复杂度为O（2n），随着文件分块的增多，复杂度会呈现指数型增长，因此，本文方案不适合文件块过多的文件存储。

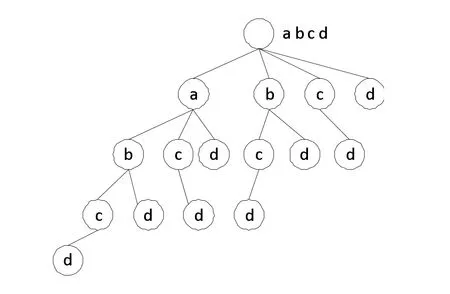
图2　文件块组合示意图

解码过程中，由于存储块类型不是固定的，所以只能计算最糟情况下还原的复杂度。存储文件块的数目也不是固定的，所以在这里将文件分n块，存储的块数为m。在最糟情况下，所有原始文件块都没有被存储，而且两两编码块之间编码过后不能还原出原始文件块，每个原始文件块的还原复杂度为O（nlog2m），还原出原始文件的需要还原n次，所以总的复杂度为O （nlog2m）。

与纠删码相比，使用这个方案，文件大小会增大，但是可靠性会明显增加，而且不需要文件的总块数是素数；缺点是增加了大量线性运算，不过增加的运算与增加的可靠性相比是值得的，特别是在某些特殊的情景下，需要保证文件可读的时候，存储空间的价值会降低。因此，在重要文件的存储上使用本文方案是有应用价值的。

3　结语

本文方案最大的优化是容错能力。容错能力不再是简单的容一错、容二错，而是根据文件分块和编码情况来决定，只要文件分块超过5以上，容错能力就会提高很多倍。缺点是编码运算比之前多。不过都是线性运算，相对于容错能力的提高，线性运算的增加是可以接受的；而对于一些重要而又不是常用的文件来说，可靠性的需求比空间需求更重要，所以，在针对这些文件，牺牲存储空间来保证文件的可靠性是必须的。在存储设备越来越大的大数据时代，普通用户可以通过本文方案，牺牲平时用不上的空间，实现对一些重要文件的的保护。特别是一些忘了备份或者没时间备份的文件。

［1］NAGAVARAPU S.A Review of Disaster Recovery Techniques and Online Data Backup in Cloud Computing［J］.2015.

［2］Geer D.Reducing the Storage Burden Via Data Deduplication［J］.Computer，2008（12）∶15-17.

［3］Xu W，Luo J.The Research on Electronic Data Backup and Recovery System Based on Network［C］//2015 International Conference on Intelligent Systems Research and Mechatronics Engineering.Atlantis Press，2015.

［4］Ahlswede R，Cai N，Li S Y R，et al.Network Information flow［J］.Information Theory，IEEE Transactions on，2000，46（4）∶1204-1216.

［5］王禹.分布式存储系统中的数据冗余与维护技术研究［D］.华南理工大学，2011.

［6］Dimakis A G，Ramchandran K，Wu Y，et al.A Survey on Network Codes for Distributed Storage［J］.Proceedings of the IEEE，2011，99 （3）∶476-489.

［7］Li S Y R，Yeung R W，Cai N.Linear Network Coding［J］.Information Theory，IEEE Transactions on，2003，49（2）∶371-381.

［8］Byers J W，Luby M，Mitzenmacher M，et al.A Digital Fountain Approach to Reliable Distribution of Bulk Data［C］.Probabilistic Methods Applied to Power Systems，2006.PMAPS 2006.International Conference on.IEEE，2006∶1-6.

［9］Reed I S，Solomon G.Polynomial Codes Over Certain Finite Fields［J］.Journal of the Society for Industrial and Applied Mathematics，1960，8（2）∶300-304.

［10］Luby M.LT codes［C］//null.IEEE，2002∶271.

［11］Shokrollahi A.Raptor codes［J］.Information Theory，IEEE Transactions on，2006，52（6）∶2551-2567.

［12］Blaum M，Brady J，Bruck J，et al.EVENODD∶An Efficient Scheme for Tolerating Double Disk Failures in RAID Architectures［J］. Computers，IEEE Transactions on，1995，44（2）∶192-202.

［13］Xu L，Bruck J.X-code∶MDS Array Codes with Optimal Encoding［J］.Information Theory，IEEE Transactions on，1999，45（1）∶272-276.

［14］Huang C，Xu L.STAR∶An Efficient Coding Scheme for Correcting Triple Storage Node Failures［J］.Computers，IEEE Transactions on，2008，57（7）∶889-901.

［15］Hafner J L.WEAVER Codes∶Highly Fault Tolerant Erasure Codes for Storage Systems［C］.FAST.2005，5∶16-16.

［16］Blomer J，Kalfane M，Karp R，et al.An XOR-Based Erasure-Resilient Coding Scheme［J］.1999.

［17］朱云锋.分布式存储系统中基于纠删码的容错技术研究［D］.中国科学技术大学，2014.

詹首道，在读研究生，研究方向为网络编码

龚洪波，在读研究生，研究方向为量子计算与量子信息

Fountain Code；Encoding；Backup；Robustness

A Scheme of Local Data Storage and Backup Based on Fountain Codes

ZHAN shou-dao，GONG hong-bo
（Department of Computer Science of Technology，Guangdong University of Technology，Guangdong 510006）

Proposes a data backup scheme which is based on fountain coding and network coding.This scheme is based on the idea of fountain coding and network coding，and it has the characteristics of erasure codes.When data are stored，the file blocks will be encoded then produce a lot of encoding blocks，after that the original block and file encoding block will be selected to storage and the store data is mixed with the original block and the encoding block so the file storage space becomes larger.When data are read，the original data can be recovered by a simple calculation which is generally linear operations.This scheme obtains the reliability of data by exploiting the space and calculation，it has a better robustness in some application scenes.

1007-1423（2016）20-0045-05

10.3969/j.issn.1007-1423.2016.20.009

2016-04-25

2016-07-05