汽车挡风玻璃除霜性能数值模拟及优化

汤柱良，袁侠义，彭丽娟，陈　林（广州汽车集团股份有限公司 汽车工程研究院，广州　511434）

汽车挡风玻璃除霜性能数值模拟及优化

汤柱良，袁侠义，彭丽娟，陈林
（广州汽车集团股份有限公司 汽车工程研究院，广州511434）

利用CFD方法对某汽车挡风玻璃的除霜过程进行数值模拟，针对单送风口结构除霜气流过于集中，导致挡风玻璃A区除霜过慢的问题，采用双送风口结构并建立其三阶响应面模型，利用遗传算法，以传热系数为优化目标，对吹风角度进行优化，消除了除霜死角，提高了除霜效率。

计算流体动力学；除霜性能；挡风玻璃

1　问题的提出

汽车挡风玻璃结霜起雾是汽车行驶过程中经常遇到且需要解决的问题。它在很大程度上会影响到驾驶员的视野，造成严重的安全隐患，良好的挡风玻璃除霜性能，是汽车设计阶段一项重要工作。为满足驾驶员前方180°视野范围，国标GB 11555-2009中明确规定了除霜时间限制：20 min时A区域有80%已完成除霜，25 min 时A'区域有80%已完成除霜，40 min时B区域有95%已完成除霜［1］。

由于传统实验或经验设计方法周期长，花费成本高，因此，CFD方法受到国内外学者的重视。文献［2］使用STAR-CD实现了对前挡风玻璃除霜除雾效果的数值模拟。文献［3-6］将数值仿真结果与试验进行对比分析，验证了CFD方法的准确性，文献［7］分析了气流从矩形出风口冲击固定倾斜壁面的流体热参数，将仿真结果与试验进行对比。文献［8］对除霜风道流动情况进行数值模拟，针对除霜风道压力损失较大、出风速度不均等问题，对风道结构进行改进。前人研究成果对除霜效果具有一定的提高，并部分成功用于实车，但针对提高影响驾驶员视野区域除霜效率的研究较少。基于此，本文对某轿车驾驶室乘员舱离散化，利用CFD软件模拟汽车挡风玻璃的除霜性能。针对单吹风口除霜气流过于集中、除霜效率不高的问题，提出优化改进措施，采用双吹风口型式，以A、B区的传热系数为优化目标。通过DOE方法选取20组样本点，建立响应面模型，采用遗传算法对该模型进行优化设计，寻找最适合的吹风角度，将优化后的模型与仿真结果对比，得出最终除霜效果。

2　计算方法与CFD模型

2.1数学模型

除霜是指除霜送风口射出温度较高的气流，通过对流换热与玻璃的导热使玻璃外表面的霜层融化的过程。乘员舱内的流动为不可压缩流，RNGk-ε湍流模型通过修正湍流黏度考虑了平均流动中的旋转流动情况，能够较好地模拟乘员舱内的流动。文中即采用该湍流模型，在壁面附近的粘性层中采用壁面函数法［9］。

针对霜层的融化过程，本文采用瞬态计算方式，瞬态计算时车内流场的能量方程［10］如下：

把冰水混合层看作一种流体，根据固态温度和液态温度定义液相分数来判定每个单元的相变状况，玻璃外侧的冰霜层采用如下能量方程：

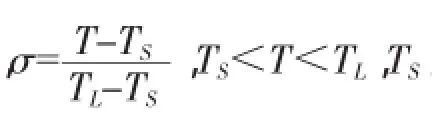
2.2物理模型

本文采用的模型为某款轿车的乘员舱，考虑了座椅、内饰等细节，并对网格质量影响较大的区域如仪表盘、方向盘做了适当简化。根据国标规定，将挡风玻璃分为A、A'、B三块区域，简化后的物理模型如图1所示。

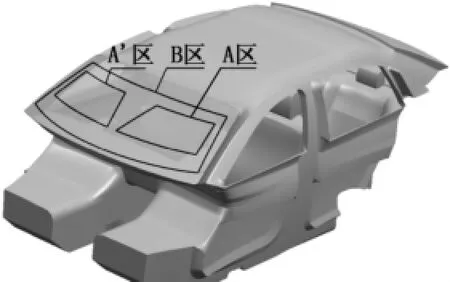
图1　乘员舱物理模型

2.3网格划分及边界条件设置

运用ICEM对乘员舱内空气采用四面体网格进行离散，对A区和B区采用分区域划分的方法，玻璃和霜层采用棱柱体网格划分，总的网格单元数为129万个，其中乘员舱内流体网格119万个，玻璃为四层棱柱体网格共1.08万个，霜层为五层棱柱体网格共1.36万个。划分好的网格如图2所示。

图2　全局网格和玻璃网格划分

边界条件设置：除霜送风口设为速度入口边界，速度大小为3.2 m/s；瞬态计算过程中送风温度为308 K；出风口设为压力出口，大小为0.1 MPa；其余边界设为静止壁面；空气与玻璃、玻璃与霜层之间均为热耦合边界；将霜层视为一种流体［11］；定义了两种流体材料和一种固体材料，分别为车内空气、冰霜层、玻璃，玻璃厚度4 mm，霜层厚度0.5 mm，其物性参数见表1。

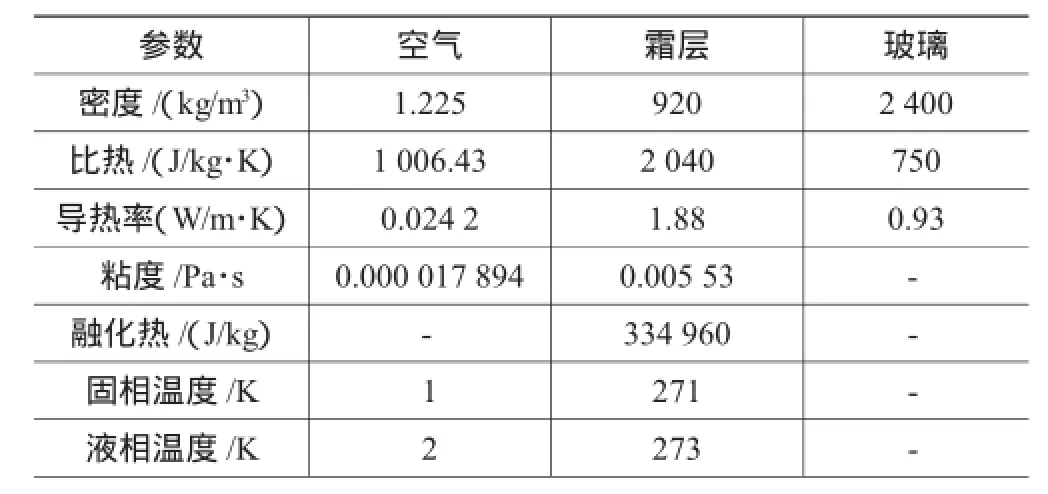
表1　空气、冰霜层和玻璃的物理参数

3　计算结果分析及优化改进

3.1计算结果分析

通过CFD模拟分析，得到挡风玻璃内侧的流场迹线如图3所示。由于吹风口位于玻璃中间区域，气流相对集中，而流经对驾驶员视野影响较大的区域气流较少，A区除霜缓慢，两边的霜层难以除尽，有必要对其进行改进。

研究对象为2011—2016年期间的郑州市创新型城市建设情况，投入类指标从人、财、物方面反映了规模以上工业企业的核心资源投入，产出类指标从创新效果方面反映了规模以上工业企业的核心能力发展结果，所有指标均为正向指标。为了剔除物价变化影响，有关名义变量数值使用定基2010年的工业生产者出厂价格指数进行平减以转化为实际变量数值。在DEAP软件中，选择投入主导、规模报酬可变与多阶段算法的DEA结果(见表2)。

图3　挡风玻璃内侧的流场迹线图

对单吹风口型式挡风玻璃的CFD结果分析后认为，要实现A、B区的快速除霜，减少死角，可改用双吹风口型式。双吹风口的CFD流场迹线如图4所示，流场与之前相比更加合理。

图4　挡风玻璃内侧的流场迹线图

3.2优化目标与设计变量

与单一吹风口不同，双吹风口型式的吹风角度分为碰撞角和平面角。它们决定了气流方向和冲击点位置，碰撞角和平面角过大或过小都会导致除霜气流与玻璃内表面发生分离，存在最佳角度。因此，有必要对其进行优化。图5为碰撞角φ与平面角β的示意图。

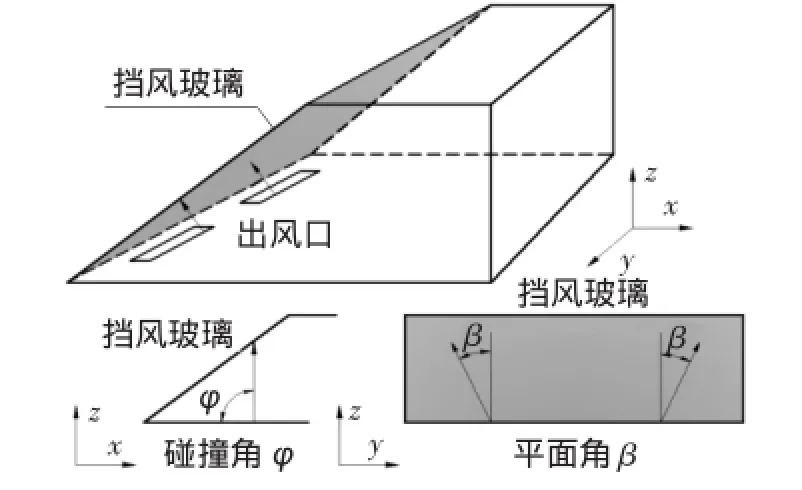
图5　气流碰撞角和平面角示意图

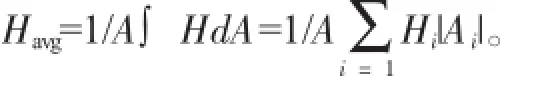
由于汽车前挡风玻璃A区和B区为重点关注区域，因此，以A、B区的平均传热系数Ha、Hb为目标函数，以碰撞角φ与平面角β为优化目标，优化问题描述如下：

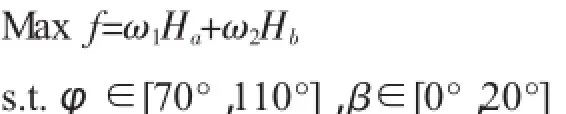
式中：ω1、ω2为权重系数，由国标GB11555-2009规定，A区应优先完成除霜，取权重系数分别为0.6、0.4。

对平面角和碰撞角采用DOE方法中的正交试验法确定20组设计样本点，导入CFD软件求解器计算得出20组样本值，将样本值运用最小二乘原理建立三阶响应面模型，即H关于φ和β的三次多项式。

建立响应面模型后，对其拟合程度进行验证，通过方差分析中的决定参数R2检验，用来评价构建的近似模型与真实模型之间的误差，定义如下：

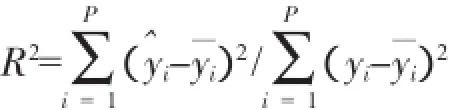
P是设计点的个数；i是自由度，其值为调整参数的个数减1；y、y 、y分别是响应量的实测值、预测值以及响应量实测值的平均值。如R2=1说明近似模型与真实模型在每一个样本点上均完全吻合，此处的R2=98.8% 和96.1%，均在90%以上。可见三阶响应面模型可以精确地描述设计变量和响应之间的关系。

3.4优化分析

本文选用遗传算法对建立的近似模型进行寻优，获取近似模型的最优解，将最优解进行CFD仿真分析，在获得最优解的同时提高优化效率［12］。

设置初始种群个体数为30，进化繁殖100代，最终得出模型最优点φ=100.2°，β=14.9°。对最优点进行CFD仿真计算，得出的数值与近似模型得出的结果误差在3%以内，如表2所示。由于优化权重不同，Ha、Hb优化量不一致，优化后A区的平均传热系数为13.46 W/m2·K，B区的平均传热系数为13.27 W/m2·K，与优化前相比分别提高18.9%和5.1%，具体见表3。

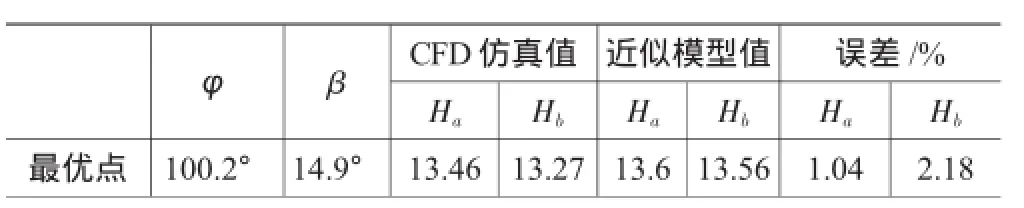
表2　最优点仿真值与近似模型响应值对比

表3　优化前后传热系数（W/m2·K）对比

霜层的平均液相率σavg=1/A∫ σdA，表示了全部霜层融化的比例。平均液相率等于1，说明霜全部融化为液态水。图6为优化前后除霜过程中A、B区霜层的平均液相率随时间的变化情况。由图6可知，优化前A、B区域霜层平均液相率达到0.9，即融化90%所需时间分别为1 200 s、1 350 s，优化后分别为750 s、880 s，减少了450 s、470 s，除霜时间大大缩短。

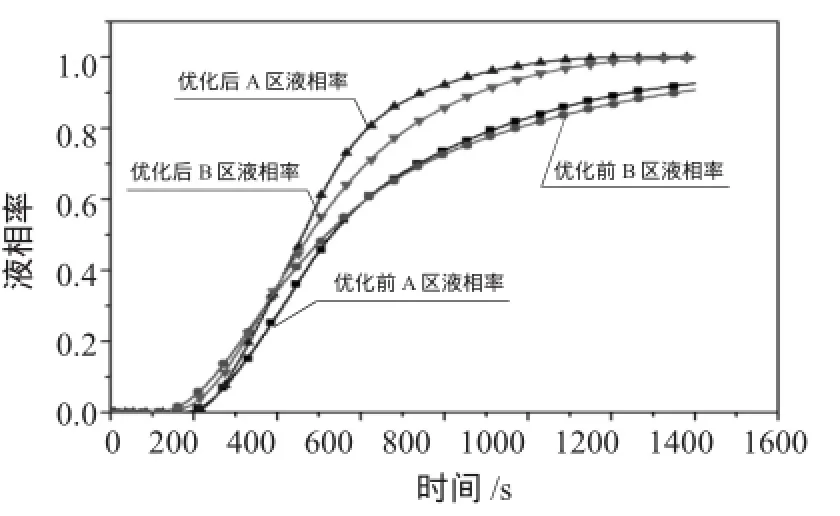
图6　优化前后平均液相率随时间的变化

图7和图8为优化前后玻璃近壁面速度云图和霜层的液态分布图。从图中可以看出，初始吹风角度下气流存在重叠区域，而玻璃两侧气流较少，导致两侧除霜缓慢，A、B区除霜缓慢；优化后气流重点吹向A区和B区，减少了气流重叠区域。除霜初始阶段存在较大V型区域。随着时间推移，逐渐消失，到 1 200 s时B区霜层基本融化，符合国标规定。

图7　优化前后玻璃近壁面速度云图

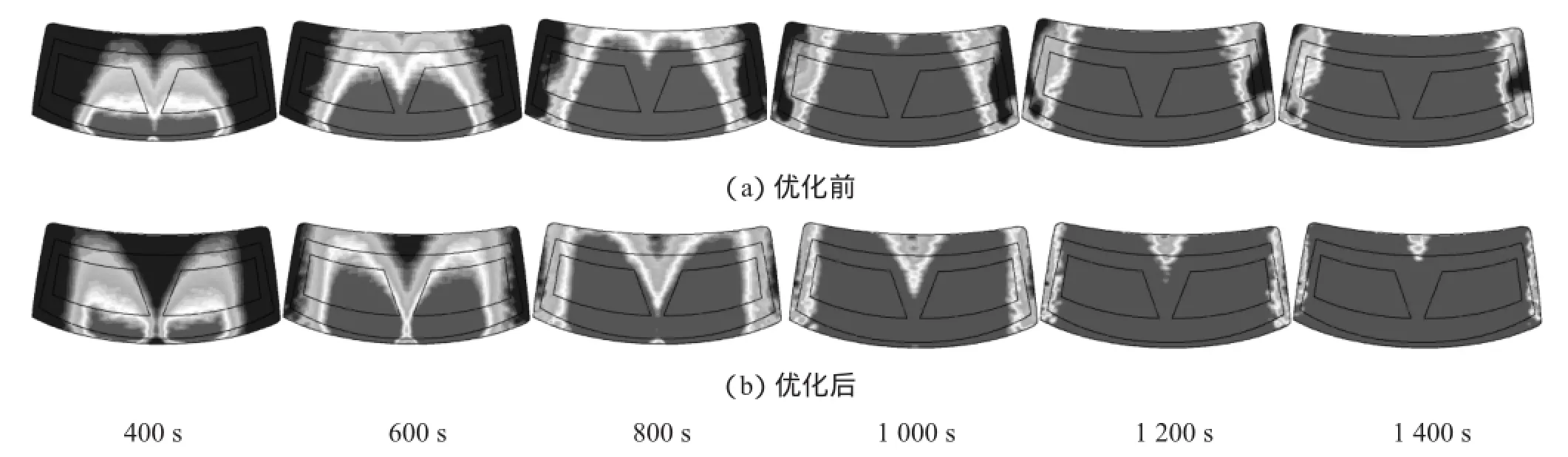
图8　优化前后不同时刻霜层的液态分布图

4　结论

本文在分析了原有除霜系统的基础上，对除霜吹风口进行改进，以吹风角度为设计变量，建立近似模型进行优化，使挡风玻璃的除霜性能得到明显改善。具体结论如下：

1）双吹风口比单吹风口的气流分布合理，能提高A、B区的除霜效率，同时解决了除霜死角的问题。

2）建立三阶响应面模型，采用遗传算法对吹风角度进行优化，在保证精度的同时节省了计算资源。通过优化前后对比分析，A区和B区的传热系数分别提高了18.9%和5.1%。

3）将最优角度应用到除霜分析，A区和B区除霜90%所需时间分别减少了450 s、470 s，效果明显。

［1］全国汽车标准化技术委员会.汽车风窗玻璃除霜和除雾系统的性能和试验方法：GB 11555－2009［S］.北京：中国标准出版社，2009：9.

［2］邓峰，谷正气，杨易，等.汽车前风窗玻璃除霜除雾数值模拟分析和研究［J］.汽车工程，2009，31（2）：175-179.

［3］张晓兰，施俊业，陈江平.汽车挡风玻璃除霜性能数值模拟［J］.汽车工程，2007，29（11）：1009-1013.

［4］董素艳.客车挡风玻璃除霜性能试验与数值模拟［J］.系统仿真技术［J］.2011，7（3）：190-195.

［5］王俊，陈如意.汽车除霜系统性能CFD分析与试验［J］.汽车技术，2011，（4）：4-7.

［6］Robert A.Brewster，Steffen Frik and Frank Werner.ComputationalAnalysisof AutomotiveWindshieldDe-Icing with Comparison toTest Data［J］.SAE Paper 971833：469-483.

［7］Subrata Roy，Paresh Patel.Study of Heat Transfer for a Pair of RectangularJetsImpingingonanInclinedSurface［J］.International Journal ofHeat and Mass Transfer，2003，46：411-425.

［8］朱娟娟，苏秀平，陈江平.汽车空调除霜风道结构优化研究［J］.汽车工程，2004，26（6）：747-749.

［9］孟庆超，谷正气，何忆斌.轿车室内流场的数值模拟研究［J］.系统仿真学报，2008，20（7）：1700-1702.

［10］Haribalan Kumar，Subrata Roy.Improved De-icing of an Inclined Windshield Surface［J］，American Institute of Aeronautics and Astronautics Paper No.2005-0187.

［11］S.J.Kang，M.F.Kader，Y.D.Jun，et al.Automobile DefrostingSystem Analysis Through a Full-scale Model［J］.International Journal ofAutomotive Technology，2011，12（1）：39-44.

［12］韩瑞锋.遗传算法原理及应用［M］.北京：兵器工业出版社，2010.

修改稿日期：2016-02-11

Numerical Simulation and Optimization of a Vehicle Windshield Defrosting Performance

TangZhuliang，Yuan Xiayi，PengLijuan，Chen Lin
（GACAutomotive EngineeringInstitute，Guangzhou 511434，China）

The authors use CFD method to simulate a vehicle windshield defrosting processes.Aiming at the problemwhich area Aofwindshield defrosts tooslowlybecause ofthe defrostingairflowofthe single outlet structure beingtooconcentrated，theyadopt the double outlet structure and establish its cubic surface response model.Then they take the jet impingement angles as design variables，take the heat transfer coefficient as objective function tooptimize the defrost system by use ofthe genetic algorithm.The results showthat the defrosting blind area is eliminated，and the defrostingefficiencyis improved.

computational fluid dynamics（CFD）；defrostingperformance；vehicle windshield

U461.1

B

1006-3331（2016）04-0049-04

汤柱良（1988-），男，研究方向：汽车空气动力学。