天然气体系三相平衡计算交互作用因子Kij的取值
李浩勇 王登海 耿树博 郑 欣 赵 丹 王文珍
1.西安石油大学 2.长庆科技工程有限公司
天然气体系三相平衡计算交互作用因子Kij的取值
李浩勇1王登海2耿树博1郑 欣2赵 丹1王文珍1
1.西安石油大学2.长庆科技工程有限公司
为解决LNG产业链中的重烃析出问题,研究建立了天然气体系三相相平衡理论模型并自主研发了热力学计算软件。计算模型中的Kij代表纯物质变成混合物时所有的物理性质变化,是温度、组成以及组分性质的函数。目前对于物质混合过程的物理化学变化没有全面的认识,所以Kij没有具体的表达式。计算了天然气混合体系中不同Kij的相平衡计算,以选取合适的Kij值来提高模型计算结果的准确性。
液化天然气交互作用因子相平衡逸度计算
我国天然气消费量大,东西部天然气分布与消费极不平衡,液化天然气技术成为我国中短距离运输天然气的主要方法[1-3]。在液化流程中,天然气在许多设备中处于低温状态,其重烃等组分在低温下会形成固相,堵塞管道、阀门,给生产造成事故和危害。所以,有效地脱除天然气中的重烃是天然气液化流程中非常重要的技术环节[4-11]。本文通过自主研发的热力学计算软件,研究建立了天然气体系三相相平衡理论模型并进行了计算,为天然气的液化工艺设计提供了可靠的数据支持和基础理论依据。
建立完善的相平衡计算体系,首先要保证计算结果的准确性和精度。在本模型中有很多影响计算精度的因素,如状态方程、混合规则以及交互作用因子[12-15]。状态方程和混合规则都可以根据计算目标体系的性质来选取,以便将误差减至最小,而交互作用因子Kij代表了多种纯物质变成混合体系时所有的物理性质的变化。由于目前对混合过程的物理化学机理认识还不够充分,没有一个普遍通用的Kij函数具体表达形式[16-17]。本文根据计算来确定最适合的Kij参数值,通过计算不同Kij的液相逸度并与Aspen计算结果进行分析比较,最终确定本模型Kij的最优值。
1 本模型计算的原理
本模型气液两相平衡用PR方程计算:
(1)
b=(1-Kij)(αiαjβiβj)0.5
βi=[1+(0.374 64+1.542 26ωi-
bI=0.077 8RTci/pci
Kij为交互作用因子,将在第2节讨论。

(2)

(3)

2 交互作用因子Kij的取值
2.1不同条件下Kij的取值
文献资料显示[17-18],多组分混合体系中Kij的取值一般在0到0.1之间。本文在0到0.1之间对Kij取值,计算了混合体系的液相逸度系数。计算体系组成及性质如表1所示[19]。

表1 计算体系组成及性质Table1 Compositionandpropertyofcalculationsystem组分摩尔分数组分摩尔分数氮气0.0077异戊烷0.00126甲烷0.9314正戊烷0.00113乙烷0.0273环己烷0.000486丙烷0.0148苯0.000253异丁烷0.0068庚烷0.00283正丁烷0.0054甲苯0.000641
由计算数据分析得出,Kij的取值和烃类中碳原子的数量有关系。以碳四和碳五为分界线,碳四及以下轻烃和碳五及以上重烃的Kij取值规律不同。
2.1.1碳四及碳四以下轻烃的Kij取值
碳四及碳四以下轻烃在Kij=0时的计算结果非常接近Aspen数据,误差很小:当Kij值越大时,误差越大。图1~图5为碳四以下的轻烃在Kij=0时的液相逸度系数φ和Aspen数值对比。由图1~图5中可以看出,Kij=0时,除了甲烷的误差在温度大于200 K后略微明显,其余组分液相逸度系数计算值和Aspen计算值均比较接近。

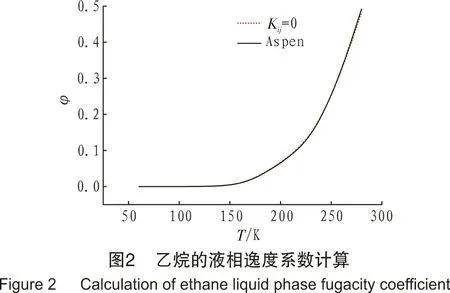



2.1.2碳五及碳五以上重烃的Kij取值
碳五及碳五以上重烃的Kij取值规律与温度有关。本文选取重烃里比较重要的两个组分环己烷和苯为例来说明重烃的Kij取值与温度的关系。表2为本模型计算的两种重烃的液相逸度系数与Aspen结果对比误差较小时的Kij取值情况。

表2 环己烷和苯的液相逸度系数Table2 Liquidphasefugacitycoefficientofcyclohexaneandbenzene温度/K对应Kij值环己烷苯模型Aspen模型Aspen800.054.20×10-194.16×10-191.01×10-189.28×10-191000.04752.97×10-143.01×10-146.39×10-146.17×10-141200.0454.67×10-114.73×10-119.30×10-119.16×10-111400.04258.96×10-098.90×10-091.68×10-081.65×10-081600.045.01×10-074.77×10-078.95×10-078.51×10-071800.031.24×10-051.26×10-052.11×10-052.17×10-052200.0156.84×10-056.39×10-059.29×10-059.65×10-052400.00752.22×10-042.10×10-042.83×10-042.91×10-042600.00256.56×10-046.29×10-048.02×10-048.14×10-0428001.74×10-031.69×10-032.07×10-032.10×10-03
根据表2的数据绘制了重烃的Kij取值和温度的关系曲线,见图6。重烃的Kij随温度的变化规律可以分为两部分:当温度小于160 K时,Kij随温度的变化为线性关系;当温度大于160 K时,Kij随温度的变化为高次多项式,关系式如式(4)所示。
本模型重点解决天然气中的重烃析出问题,所以对重烃的计算尤为重要。利用式(4)作为Kij的取值,计算了苯和环己烷的液相逸度系数,见图7和图8。由图可以看出,当Kij按式(4)计算时,重烃的相平衡计算结果和Aspen的计算结果很接近,误差很小。
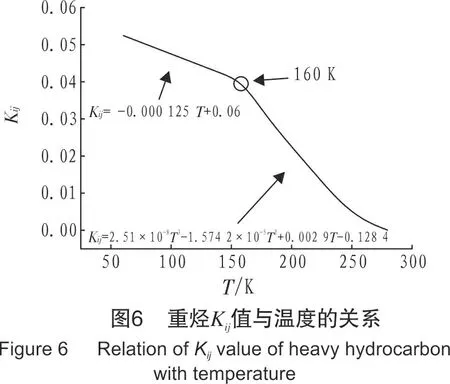
(4)


2.2压力对Kij值的影响
本研究利用5.0 MPa下的Kij公式计算了3.0 MPa和7.0 MPa下的相平衡数据。表3和表4列出了丙烷和苯的相平衡数据,丙烷代表碳四及以下的轻烃,苯代表碳五及以上的重烃。
由表3和表4可以看出,两个压力下的计算结果随Kij的变化规律和5.0 MPa下的变化规律相同。代表碳四及以下轻烃的丙烷在Kij=0时计算误差小,代表碳五及以上重烃苯的Kij取值和5.0 MPa下的取值一样。在此计算模型中,压力对交互作用因子的取值几乎没有影响。
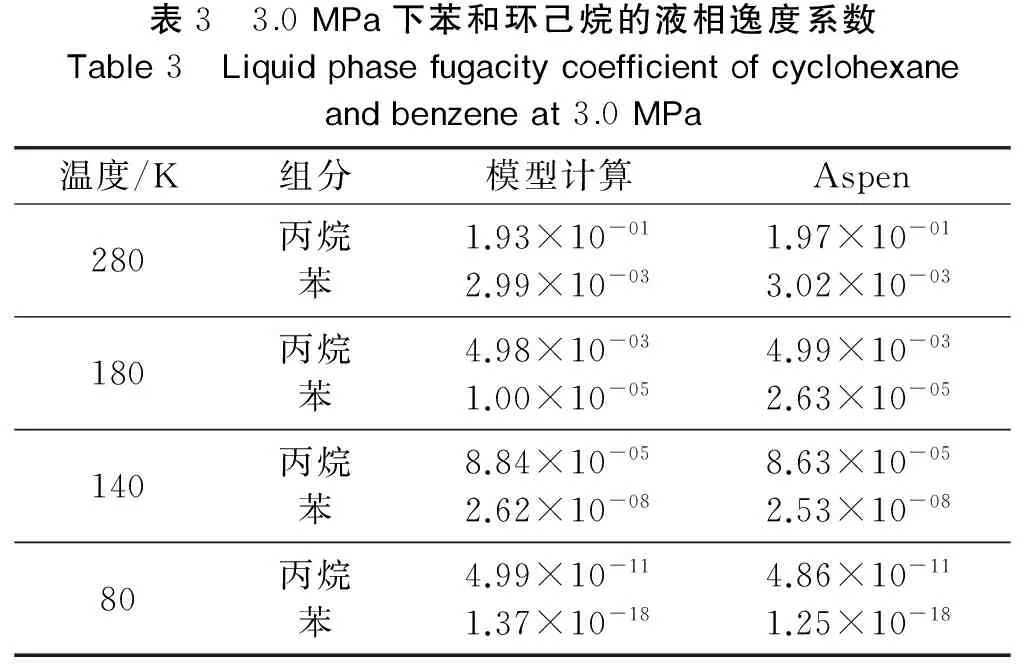
表3 3.0MPa下苯和环己烷的液相逸度系数Table3 Liquidphasefugacitycoefficientofcyclohexaneandbenzeneat3.0MPa温度/K组分模型计算Aspen280丙烷苯1.93×10-012.99×10-031.97×10-013.02×10-03180丙烷苯4.98×10-031.00×10-054.99×10-032.63×10-05140丙烷苯8.84×10-052.62×10-088.63×10-052.53×10-0880丙烷苯4.99×10-111.37×10-184.86×10-111.25×10-18

表4 7.0MPa下苯和环己烷的液相逸度系数Table4 Liquidphasefugacitycoefficientofcyclohexaneandbenzeneat7.0MPa温度/K组分模型计算Aspen280丙烷苯9.23×10-021.72×10-039.30×10-021.72×10-03180丙烷苯3.10×10-031.36×10-052.64×10-031.46×10-05140丙烷苯4.52×10-051.29×10-084.43×10-051.28×10-0880丙烷苯3.10×10-118.04×10-192.94×10-118.20×10-19
3 结 论
本文利用自主研发的热力学软件对天然气体系进行了相平衡计算,为了找到适合模型的Kij值,分别取不同的Kij值计算了不同温度压力下的液相逸度系数,并与Aspen的计算结果进行对比。结果显示,对于碳四及以下的轻烃,当Kij=0时,其计算结果准确度较高;对于碳五及以上的重烃,Kij值为温度的函数,当Kij按式(4)取值时,计算结果准确度较高。
[1] 黄志光, 汪荣顺, 石玉美, 等. 小型天然气液化装置的研制现状与前景[J]. 低温工程, 2002, 130 (6): 59-62.
[2] 邢云, 刘淼儿. 中国液化天然气产业现状及前景分析[J]. 天然气工业, 2009, 29(1): 120-123.
[3]徐文渊. 小型液化天然气生产装置[J]. 石油与天然气化工, 2005, 34(3): 161-164.
[4] HOSSEIN BEIGI H R, EDALAT M. A two parameters equation of state for phase equilibrium behaviour reservoir and liquified natural gas[J]. Society of Petroleum Engineers, 2005(6): 1-22.
[5] 赵敏, 厉彦忠. C3/ MRC液化流程中原料气成分及制冷剂组分匹配[J]. 化工学报, 2009, 60(增刊1): 50-57.
[6] SERDYUKOV, LENTRANSGAZ, KHODORKOV. Mini plants at pressure reduction stations in Russia[J]. LNG Journal, 2002 (4): 6-9.
[7] 李廷勋, 郭开华. LNG安全规范现状[J]. 天然气工业, 2008, 27(6): 1-3.
[8] 皮艳慧, 廖柯熹, 孙欧阳. 天然气水合物生成物条件预测模型及适用性评价[J]. 天然气与石油, 2012, 30(6): 16-18.
[9] 陈坚, 黄志明, 包永忠. 烷烃混合物二元相互作用参数的新型关联式[J]. 化工学报, 2006, 57(7): 1508-1512.
[10] 姚军辉,石勇. 多孔介质中天然气水合物分解热力学模型研究[J]. 石油与天然气化工, 2009, 38(1): 11-14.
[11] 曾凡平, 田广新. 液化天然气工厂重烃脱除工艺方案比选[J]. 石油与天然气化工, 2015, 44(1): 35-38.
[12] 陈振华, 曹堃, 姚臻. 基于PR状态方程的二元体系临界性质计算中不同混合规则对比[J]. 高校化学工程学报, 2008, 22(3): 365-370.
[13] JAMES M P, FRENKEL D. Numerical prediction of the melting curve of n-octane[J]. Journal of Chemical Physics, 1999, 111(4): 1500-1510.
[14] 杨帆, 陈保东, 姜文全, 等. PR方程在天然气热物性计算中的应用研究[J]. 当代化工, 2013, 42(5): 649-656.
[15] 于志家, 杨筱恬. 用SRK方程与PR方程求算双组份混合气体热力学性质[J]. 化工高等教育, 2013, 30(1): 59-62.
[16] SQUILLACOTE M, SHERIDAN R S, CHAPMAN O L. Spectroscopic detection of the twist-boat conformation of cyclohexane[J]. J Am Chem Soc, 1975, 97(11): 3244-3246.
[17] 许国华, 黄永华, 张鹏. 流体混合物热力学性质计算的混合法则新进展[J]. 制冷技术, 2002, 36(8): 31-36.
[18] 李延勋, 刘志刚. 基于PR方程的气液相平衡计算[J]. 广东工业大学学报, 1999, 16(1): 29-34.
[19] 王文珍, 王登海, 郑欣. 天然气中低碳烷烃的汽-液平衡研究[J]. 广州化工, 2014, 42(16): 13-16.
Calculation of interaction parameter on phase equilibrium in natural gas
Li Haoyong1, Wang Denghai2, Gen Shubo1, Zheng Xin2, Zhao Dan1, Wang Wenzhen1
(1.Xi’anShiyouUniversity,Xi’an710065,China) (2.ChangqingScienceandTechnologyEngineeringCo.,Ltd.,Xi’an710065,China)
To solve the heavy hydrocarbon precipitation problems in LNG industry, the theoretical model of three phase equilibrium is established and the thermodynamic calculation software is developed independently. The interaction parameterKijin calculation model represents all the physical properties changing when the pure substance becomes mixture, and it’s the function ofT,xand component properties. It can’t be calculated by a formula as physical chemistry changes of the mixing process have not been understood comprehensively now. The phase equilibrium in differentKijis calculated in order to select the appropriateKijto improve the accuracy of the model calculation results.
liquefied natural gas, interaction parameter, phase equilibrium, fugacity calculation
李浩勇(1992-),男,硕士研究生。现就读于西安石油大学,研究方向为天然气体系热力学计算及LNG热力学条件与天然气体系脱硫脱碳的研究。 E-mail:lihaoyong10@163.com
TE642
A
10.3969/j.issn.1007-3426.2016.04.008
2016-01-25;编辑:康莉
——以延长探区延长组页岩为例

