基于逸度与压力计算页岩吸附甲烷的等量吸附热差异分析——以延长探区延长组页岩为例

薛 培，张丽霞，梁全胜，师 毅

（1.西北政法大学，西安 710063；2.陕西延长石油（集团）有限责任公司研究院，西安 710075；3.延长石油集团油气勘探公司，陕西延安 716000）

0 引言

页岩气的主要赋存空间为页岩中发育的微纳米级孔隙，其赋存状态具有吸附态、游离态和溶解态等3 种形式，以吸附态和游离态为主，其中吸附气占比可达20%～85%［1］。由于吸附过程中，存在着气体分子动能及势能的变化，因此页岩气的吸附过程为放热。分析吸附过程的热力学特征有助于深入认识页岩气的吸附机理。

现有的页岩气及煤层气吸附热力学特征分析普遍采用基于Clasius-Clayperon 方程的吸附等量线标绘法来计算等量吸附热［2］，区别在于等量吸附热计算所用的等温吸附数据类型存在差异。文献［3-10］采用基于压力的等温吸附数据作为等量吸附热计算的基础数据，而文献［11-15］采用基于逸度的等温吸附数据计算等量吸附热。由于经典的Clasius-Clayperon 方程是在假设吸附气为理想气体并忽略吸附相体积的基础上推导而来［16］，然而页岩和煤等温吸附CH4过程的温度和压力范围均已超过CH4的临界点（CH4的临界温度为-82.6 ℃，临界压力为4.64 MPa），等温吸附过程属于超临界吸附的范畴［17］，因此经典的Clasius-Clayperon 方程并不适用于页岩与煤的吸附热力学特征分析，对于非理想气体的吸附热力学分析，需将Clasius-Clayperon 方程中的压力替换为逸度［18］。目前尚未见到关于逸度与压力的选择对等量吸附热计算结果影响的量化评价。

笔者以延长探区甘泉地区延长组页岩为研究对象，开展不同温度下（30～70 ℃）页岩吸附CH4的等温吸附实验及绝对吸附量的校正，对比分析逸度与压力之间的差异，以及基于逸度-绝对吸附量和压力-绝对吸附量获得的等量吸附热的差异，以期完善页岩等量吸附热的计算方法，进而明确陆相页岩吸附热力学特征。

1 页岩等温吸附实验

1.1 实验样品与方法

等温吸附实验样品来自延长探区甘泉地区延长组长7 段黑色页岩。实验样品地球化学分析表明，该样品总有机碳（TOC）质量分数为5.32%，有机质类型为Ⅱ1型，有机质成熟度（Ro）为0.97%。矿物组成分析表明，该样品黏土矿物含量较高，质量分数为52.4%，石英质量分数为24.5%，长石质量分数为14.1%，并含有少量的黄铁矿和菱铁矿［19］。

等温吸附实验共设定30 ℃，40 ℃，50 ℃，60 ℃，70℃等5 个温度点，实验压力为0.4～11.0 MPa，单个压力点下的吸附平衡时间不少于12 h，采用纯度99.99%的甲烷为吸附气。样品预处理及实验操作规范参照了GB/T 19560—2008的相关规定［20］。

1.2 过剩吸附量与绝对吸附量

延长组页岩样品等温吸附曲线如图1 所示。由于过剩吸附量表征了实际吸附相密度减去气相密度所剩部分的吸附量，过剩吸附量小于绝对吸附量。同时采用过剩吸附量计算获得的等量吸附热及初始等量吸附热小于采用绝对吸附量获得的等量及初始等量吸附热。因此需要将过剩吸附量校正为绝对吸附量，采用绝对吸附量计算等量吸附热。

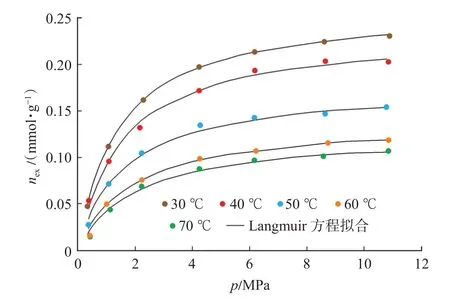
图1 延长组页岩等温吸附曲线Fig.1 Adsorption isotherm of shale of Yanchang Formation

根据Gibbs 吸附量的定义，过剩吸附量与绝对吸附量间的关系［21］为

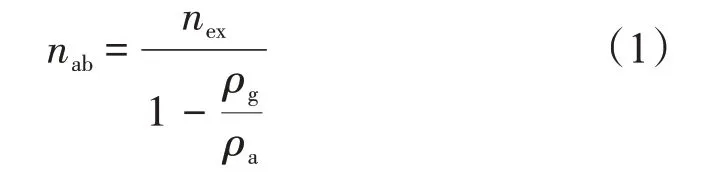
式中：nab为绝对吸附量，mmol/g；nex为过剩吸附量，mmol/g；ρg为气相密度，g/cm3；ρa为吸附相密度，g/cm3。

采用真实气体状态方程计算气相密度，气相密度可表示为

式中：M为摩尔质量，g/mol；R 为通用气体常数，8.314 J/（K·mol）；Z为真实气体压缩因子；T为绝对温度，K；P为气体压力，MPa。

本文采用Peng-Robinson 方程［22］计算压缩因子。P-R（Peng-Robinson）方程表示为压缩因子Z的形式为

参数A和B的计算方法为

式（4）、式（5）中a(T)为内聚力参数，可表示为

式中：Tc为临界温度，K；p为压力，Pa；pc为临界压力，Pa；α()T为与对比温度Tr和偏心因子ω有关的函数；b为协体积项；Tr为对比温度，Tr=T/Tc；k为与偏心因子ω有关的函数。

不同的ω取值范围内，k表达式不同，当偏心因子取值为0 ＜ω＜0.5 时，k可表示为

式中：ω为偏心因子，CH4的偏心因子取值0.008。

经计算，得出在温度为30～70 ℃、压力为0～15 MPa 时甲烷的气相密度（图2）。

图2 甲烷的密度曲线Fig.2 Density curve of CH4

由于Ozawa 等［23］经验公式法适用于较宽温压范围内的吸附相密度计算［19］，因此本文采用Ozawa经验公式法计算吸附相密度，其计算公式为

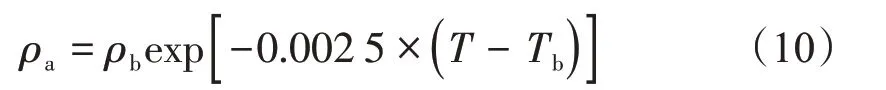
式中：ρb表示沸点密度，g/cm3（CH4的沸点密度为0.424 g/cm3）；Tb表示沸点，K（CH4的沸点为111.65 K，即-161.5℃）。

经计算，得出在温度为30～70 ℃时CH4的吸附相密度（图3）。

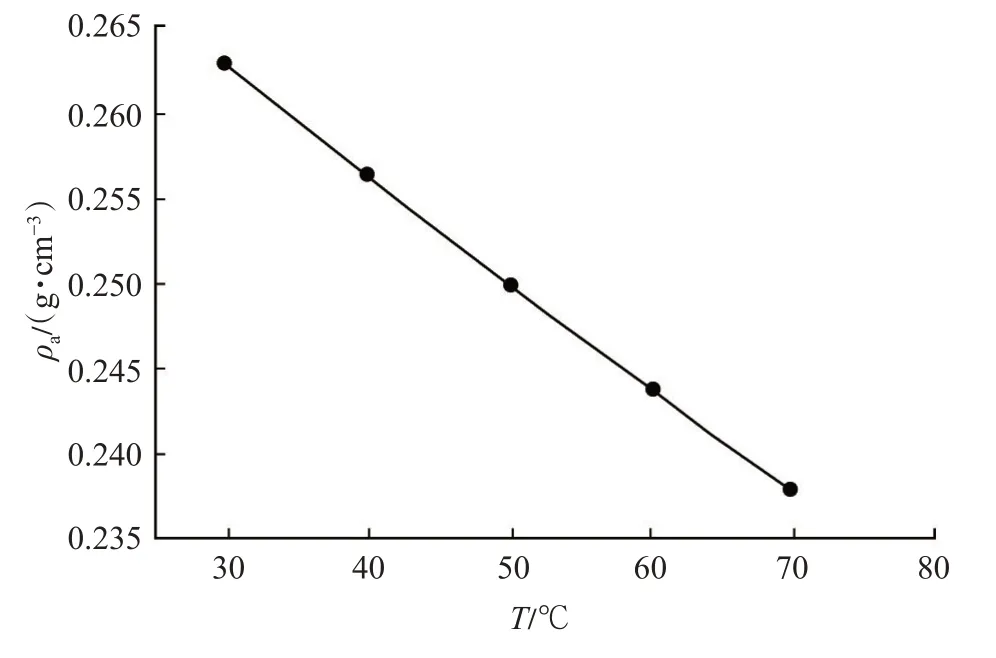
图3 甲烷的吸附相密度曲线Fig.3 Adsorbed phase density curve of CH4

基于式（1），结合CH4的气相密度（图2）和吸附相密度（图3），即可实现由过剩吸附量（图1）向绝对吸附量的校正，校正后的绝对吸附量曲线如图4所示。采用Langmuir 方程对绝对吸附量曲线进行了拟合，拟合相关系数在0.98 以上，Langmuir 方程拟合参数如表1 所列。表1 中VL-p，PL-p分别表示压力-绝对吸附量数据的Langmuir 方程拟合参数。

图4 绝对吸附量曲线Fig.4 Absolute adsorption isotherm curves

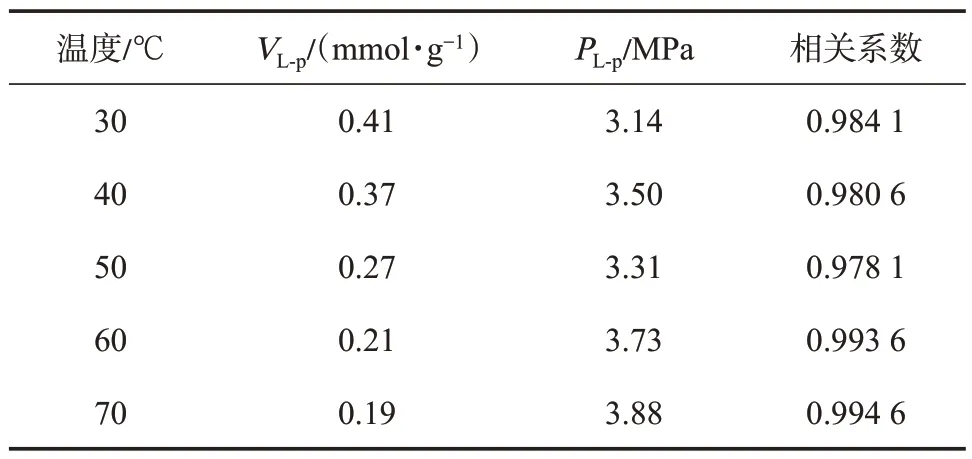
表1 压力-绝对吸附量曲线的Langmuir 方程拟合参数Table 1 Fitting parameters of Langmuir equations for the pressure-absolute adsorption isotherm

2 逸度

2.1 逸度的定义及计算方法

逸度及逸度系数是变组成体系热力学计算中的重要基本概念，也是相平衡和化学反应平衡研究的重要工具［24］。逸度是在处理非理想气体化学势时引入的概念。对于1 mol 的纯物质的热力学关系式［25］为

式中：μ为化学势，J/mol；Vm为摩尔体积，m3/mol。

对于理想气体，其状态方程为pVm=RT，则

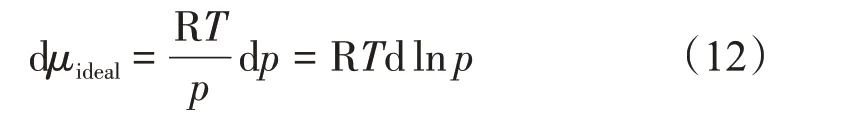
对于真实气体，其状态方程为pVm=ZRT，则

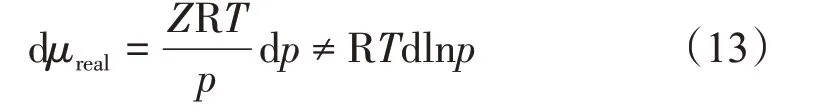
据文献［25］报道，1901 年，Lewis 提出将理想气体与真实气体的偏差放到压力项做一次性修正，并定义新函数，使得

式中：f为逸度，Pa。对于理想气体，其逸度等于压力；对于真实气体，可把逸度看作校正的压力，也表征体系的逃逸趋势。

同时定义逸度系数为

逸度系数可用来衡量真实气体偏离理想状态的程度，φ越接近1，则气体越接近理想气体。纯组分的逸度和逸度系数可采用状态方程法、图解法、对比状态法和近似法计算［26］。本文采用P-R 状态方程计算CH4的逸度，其逸度系数［18］可表示为

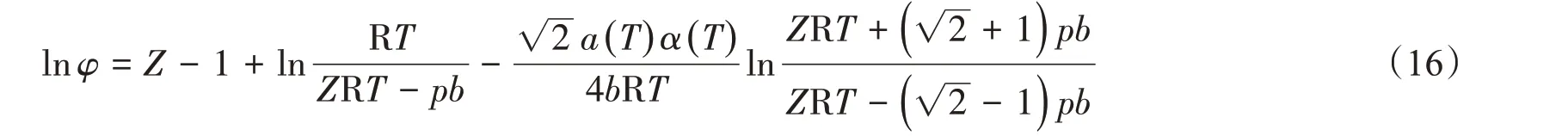
2.2 逸度与逸度系数

利用式（16）及P-R 方程即可得出逸度及逸度系数。当实验温度为30 ℃，40 ℃，50 ℃，60 ℃，70 ℃，压力为0.36～11.00 MPa 时的逸度及逸度系数曲线如图5 所示。

从图5（a）可看出，在低压力区间（0.36～2.21 MPa）内，逸度与压力基本相等，随着压力的增加，逸度与压力的差距逐渐增大。为了清晰地呈现二者的差异与温度和压力的关系，绘制了不同温度下压力与逸度差值随压力的变化曲线［图5（b）］。从图5（b）可看出，当压力大于逸度，特别是在低温高压条件下，压力与逸度的差值越发明显。具体而言，低压力阶段（0.36～2.21 MPa），压力与逸度的差值较小；处于0.002～0.010 MPa 时，温度对二者差值的影响较小；随着压力的升高，二者的差值逐渐增加，以30℃为例，压力为0.36 MPa 时，差值为0.002 MPa，当压力升高至11 MPa 时，差值增加至2.10 MPa；同时随着压力的升高，温度对差值的影响越发明显，温度越低，二者的差值越大，例如当压力为11 MPa，温度为30 ℃，40 ℃，50 ℃，60 ℃，70 ℃时，二者的差值分别为2.01 MPa，1.78 MPa，1.59 MPa，1.43 MPa，1.28 MPa。

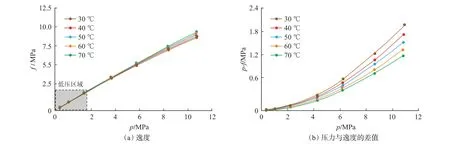
图5 逸度及压力与逸度的差值曲线Fig.5 Fugacity and difference curve of pressure and fugacity

此外，逸度系数也反映了压力与逸度的差别。由于逸度系数定义为φ=f/p，且受限于不同温压条件下逸度与压力的关系，逸度系数小于1。随着压力的升高，逸度系数逐渐降低，同时，低温条件下的逸度系数随压力增加所表现出的下降速率要大于高温条件下的下降速率（图6）。

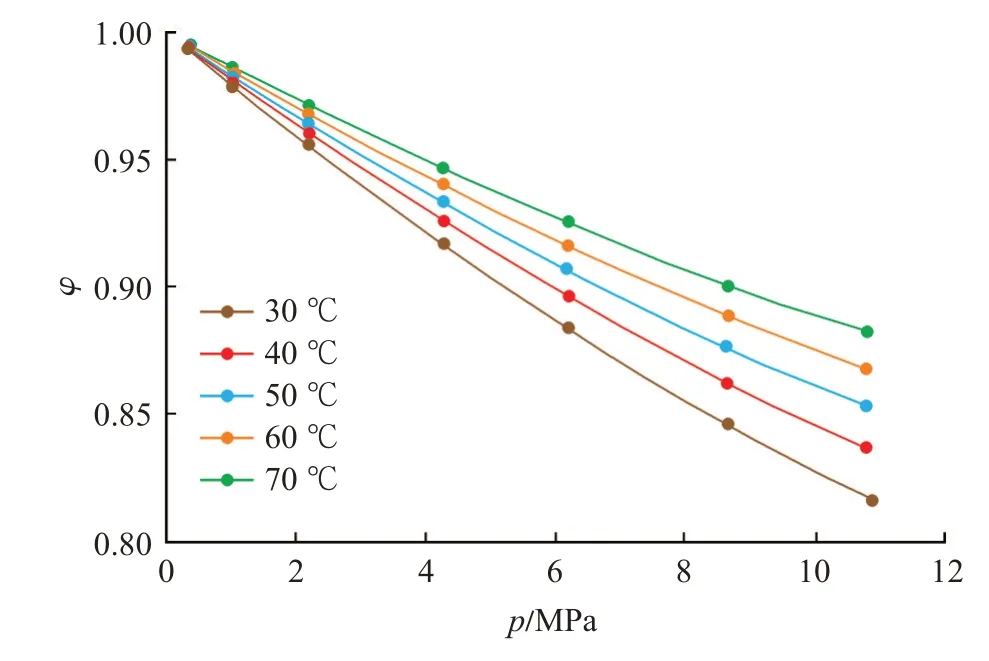
图6 逸度系数曲线Fig.6 Fugacity coefficient curve

文中采用逸度-绝对吸附量数据作为等量吸附热计算的基础数据，因此需要将图4 中以压力作为横坐标的等温吸附曲线转换为以逸度作为横坐标的等温吸附曲线，以此作为热力学分析的基础数据（图7）。由于低压力阶段，压力与逸度差值较小，而随着压力的增加，二者差值增大。因此，图7 所示的逸度-绝对吸附量曲线在高压部分数据点相对于压力-绝对吸附量曲线会向左平移，横坐标平移距离即为压力与逸度的差值，曲线形态相较于图4 所示的压力-绝对吸附量曲线发生改变。若将Langmuir方程中的参数p用逸度f替换，方程形式保持不变，对逸度-绝对吸附量数据进行了拟合。拟合结果表明，方程拟合相关系数均在0.98 以上。由于在相同的温度和压力条件下，逸度小于压力，且随着压力的升高，二者差值增大，因此相对于图4 而言，逸度-绝对吸附量的Langmuir 方程的拟合参数Langmuir体积（VL-f）及Langmuir 压力（PL-f）均略大于压力-绝对吸附量的拟合结果（表1、表2）。

图7 基于逸度的绝对吸附量曲线Fig.7 Absolute adsorption curve based on fugacity

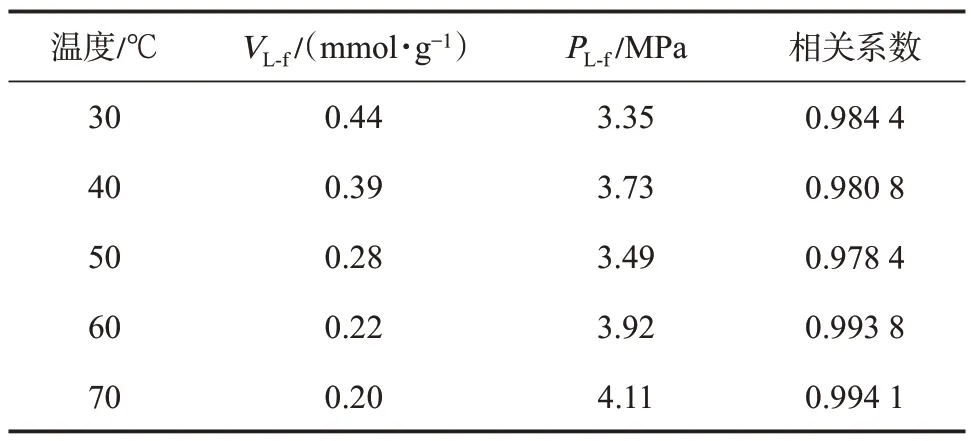
表2 逸度-绝对吸附量曲线的Langmuir 方程拟合参数Table 2 Fitting parameters of Langmuir equations for fugacity-absolute adsorption isotherm

3 等量吸附热

3.1 等量吸附热的计算方法

等量吸附热（qst）是指当压力（p）、温度（T）及吸附剂表面积（A）恒定时，吸附剂表面吸附无限小量的吸附质，吸附体系所释放的热量，其数学表达式［27］为

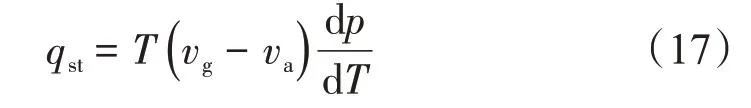
式中：qst为等量吸附热，kJ/mol；vg为体相气体的摩尔体积，m3/mol；va为吸附相气体的摩尔体积，m3/mol。

若忽略吸附相体积，且视体相气体为理想气体，则式（17）可写作经典的Clasius-Clayperon 方程［10］，即

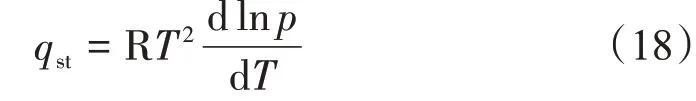
由于页岩及煤岩等温吸附CH4实验的温度和压力范围大多分别集中在20～80 ℃及0～20 MPa［28-29］，同时CH4的临界温度为-82.6 ℃，临界压力为4.64 MPa，在此温度和压力范围内的等温吸附过程存在着由气相吸附向超临界流体吸附的转变，气体分子行为已不再满足理想气体假设。以CH4压缩因子为例（图8），不同温度下CH4的压缩因子随压力的增加，先减小后增加，偏离了理想气体状态。因此针对非理想气体的热力学分析，若采用Clasius-Clayperon 方程计算等量吸附热，则需要将压力p替换为逸度f［18，30-31］，即将式（18）转变为

进而采用吸附等量线标绘法计算固-气吸附体系的等量吸附热。

基于Clasius-Clayperon 方程的吸附等量线标绘法在等量吸附热计算中应用较为广泛［2］。该方法首先需要对式（19）两端变形并积分可得

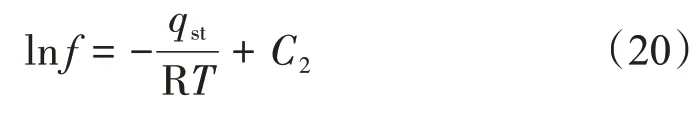
由式（20）可知，逸度的自然对数lnf与绝对温度的倒数1/T呈线性关系，由斜率得到吸附量n对应的qst。假设斜率为A，则等量吸附热计算式为

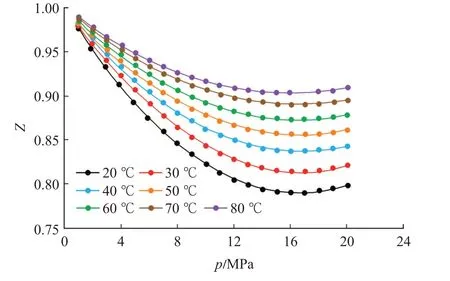
图8 CH4的压缩因子（采用P-R 方程计算）Fig.8 Compression factor of CH4by P-R equation

3.2 基于逸度与压力的等量吸附热特征对比

笔者分别采用逸度-绝对吸附量和压力-绝对吸附量数据对页岩吸附CH4的等量吸附热进行计算。同时，在后续行文过程中将基于逸度-绝对吸附量数据获得的等量吸附热标记为qst-f，相对应地将基于压力-绝对吸附量数据获得的等量吸附热标记为qst-p，以便区分。

首先，依据lnp-nab及lnf-nab的数据特征分别选用线性函数和幂函数对lnp-nab及lnf-nab进行了拟合（图9）。拟合结果表明，lnp与nab呈明显的线性关系，lnf与nab呈明显的幂函数关系，函数拟合相关系数均超过0.99。

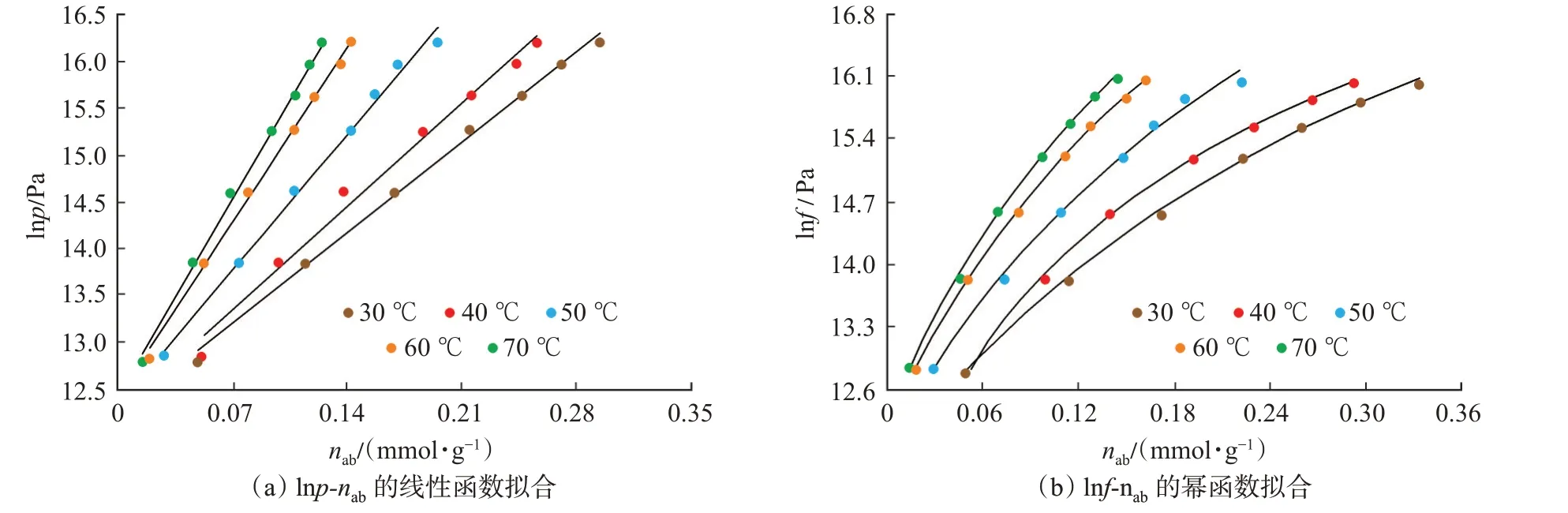
图9 lnp-nab及lnf-nab数据的函数拟合Fig.9 Fitting curve of lnp-naband lnf-nab

利用拟合得到的lnp-nab与lnf-nab的线性函数、幂函数分别计算不同绝对吸附量下的lnp及lnf，进而绘制不同绝对吸附量下的lnp-1/T 及lnf-1/T曲线，并分别对曲线进行线性函数拟合（图10），lnp-1/T及lnf-1/T曲线均符合线性相关性，且相关系数均超过0.95。

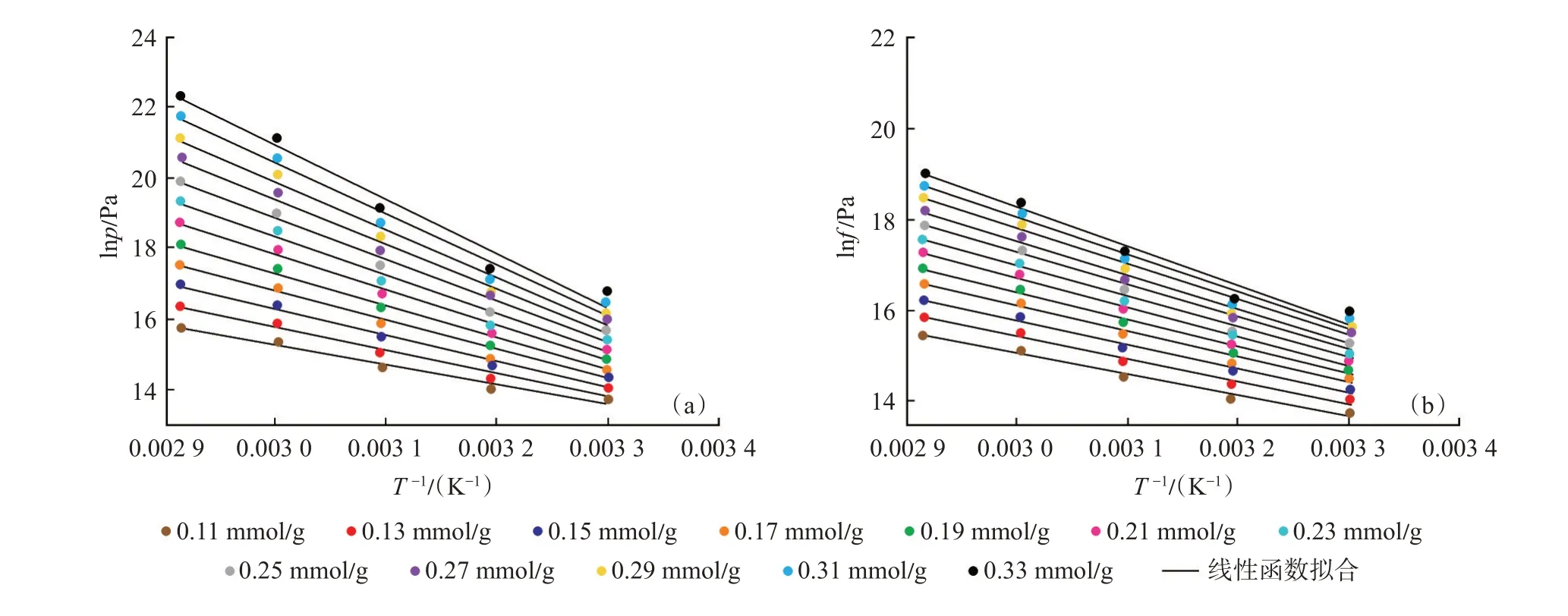
图10 lnp-1/T（a）及lnf-1/T（b）数据的线性函数拟合Fig.10 Linear fitting curves of lnp-1/T（a）and lnf-1/T（b）

分别利用lnp-1/T［图10（a）］及lnf-1/T［图10（b）］曲线线性拟合函数的斜率结合式［式（21）］计算基于压力-绝对吸附量及逸度-绝对吸附量的等量吸附热，计算结果如图11 所示。

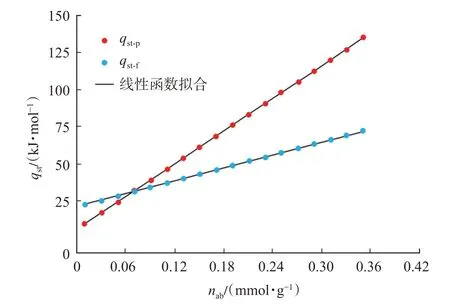
图11 基于逸度-绝对吸附量及压力-绝对吸附量获得的等量吸附热Fig.11 Isosteric heat of adsorption based on fugacity-ab‐solute adsorption isotherm and pressure-absolute adsorption isotherm

基于逸度的等量吸附热及基于压力的等量吸附热均与绝对吸附量满足良好的线性关系，相关系数均在0.99 以上（表3），且随着绝对吸附量的增加，等量吸附热均逐渐升高（图11）。绝对吸附量由0.01 mmol/g 上升至0.35 mmol/g 时，基于逸度的等量吸附热为22.31～72.35 kJ/mol，基于压力的等量吸附热为9.59～134.97 kJ/mol。

等量吸附热的大小与固体表面的强/弱吸附位点分布的均一性及吸附气分子间作用力有关［32］。吸附过程中，气体分子会优先在固体表面的强吸附位点吸附，随着吸附的进行，当强吸附位点吸附逐渐饱和后，气体分子逐步在弱吸附位点吸附，这造成了等量吸附热随着吸附量的增加而降低；同时，随着吸附量的增加，固体表面的吸附态分子密度增加，吸附气分子间的作用力增加，这造成了等量吸附热随吸附量增加而升高。由此可见，CH4在甘泉地区长7 段泥岩孔隙表面的吸附过程中，吸附质分子间的作用力是存在的，且相对于吸附剂表面的非均一性，前者吸附质分子间的作用力对等量吸附热的影响是主要的。

表3 等量吸附热曲线的线性函数拟合参数Table 3 Linear function fitting parameters of isosteric heat of adsorption

在采用等量吸附线标绘法计算等量吸附时，压力或逸度的选择并不会改变等量吸附热曲线的线性单调性特征，二者均反映了等量吸附热具有明显的单调递增的线性特征。区别在于，基于逸度的等量吸附热（qst-f）曲线的斜率小于基于压力的等量吸附热（qst-p）曲线。由于等量吸附热随吸附量增加而上升是受吸附质分子间相互作用的影响，随着吸附的进行，吸附剂表面吸附位点对吸附质分子的作用力逐渐减弱，等量吸附热曲线将更多地反映出吸附质分子间作用力的影响。因此可以认为，若采用压力-绝对吸附量计算等量吸附热，则会造成等量吸附热计算结果中吸附质分子间作用力的影响过大。

此外，在绝对吸附量小于0.065 mmol/g时，基于逸度的等量吸附热（qst-f）大于基于压力的等量吸附热（qst-p）；绝对吸附量大于0.065 mmol/g 时，前者（qst-f）小于后者（qst-p）；二者在绝对吸附量为0.065 mmol/g处曲线相交。为定量评价逸度与压力在等量吸附热计算结果中的误差，引入相对误差（δ）的概念，即

经计算，绝对吸附量为0.01～0.35 mmol/g 时，相对误差为-86.54%～57.01%（图12），若以±5%作为合理的相对偏差范围，那么仅在绝对吸附量为0.060～0.074 mmol/g 时，相对偏差处于合理范围。特别在低吸附量，即低压力阶段，基于逸度与压力的等量吸附热仍然具有较高的误差。例如，当低吸附量为nab=0.01 mmol/g 时，相对偏差高达52%。其原因在于，虽然在低压力条件下，压力与逸度的差值较小，但在高压力阶段，逸度与压力的差值较大，致使高压阶段中逸度-绝对吸附量曲线的形态与压力-绝地吸附量曲线存在较大的差异，进而影响到吸附等量线标绘法计算过程中lnp-nab与lnf-nab曲线的拟合函数发生改变，因此在低压阶段，基于压力与逸度的等量吸附热曲线出现了较高的相对偏差。由此可见，采用压力-绝对吸附量作为计算等量吸附热的基础数据，会造成较大的误差。

图12 等量吸附热的相对偏差Fig.12 Relative deviation of isosteric heat of adsorption

4 结论

（1）在低压力区（0.36～2.21 MPa）内，逸度与压力基本相等，随着压力的升高，逸度逐渐小于压力，且温度越低，压力越高，压力与逸度的差值越大。

（2）采用吸附等量线标绘法计算等量吸附热时，压力与逸度的选择并不会改变等量吸附热曲线的线性单调性特征，二者均反映了等量吸附热具有明显的单调递增的线性特征，但若采用压力-绝对吸附量计算等量吸附热，则会造成等量吸附热计算结果中吸附质分子间作用力的影响过大。

（3）基于逸度的等量吸附热与基于压力的等量吸附热的相对偏差为-86.54%～57.01%，仅在绝对吸附量为0.060～0.074 mmol/g时，二者的相对偏差处于±5%的合理范围内。页岩气吸附体系的热力学评价应当采用逸度-绝对吸附量数据作为等量吸附热计算的基础数据。