基于加权组合的海杂波多重分形建模方法

鲍星星

（河海大学 江苏 南京 210000）

基于加权组合的海杂波多重分形建模方法

鲍星星

（河海大学 江苏 南京 210000）

文中研究了一种海杂波多重分形建模方法，其主要是对以往加权组合的海杂波多重分形模型在复杂度方面提出了改进。以往加权组合的海杂波多重分形模型是大量单一的分数布朗运动在概率意义上的线性组合，模型的复杂度主要取决于两个方面：一是模型在建模过程中需要多次判别寻优以得到与建模输入海杂波特性相似的仿真数据，二是为了保证建模输出的仿真数据具有与输入海杂波较为相似的多重分形特性，需要有足够多的单一分形序列参与加权组合。本文的模型依然是采用加权组合的方法进行建模，但运用复合分数布朗运动替代单一分形序列进行加权组合建模，模型主要利用了复合分式布朗运动具有多重分形特性这一优势，大大减少了参与加权组合的分形信号的数量，在达到以往加权组合模型在多重分形特性的仿真效果基础上，降低了模型的复杂度。

加权组合；多重分形；复合分式布朗运动；单一分形序列；海杂波

研究表明：散射信号中携带了散射表面的分形特性。雷达目标回波是雷达照射到海面上目标物体所形成的散射回波，与此同时，该目标回波中也携带了雷达照射到海面形成的散射回波；即目标回波中包含了干扰目标检测的海杂波。因此，在雷达目标检测领域，海杂波能否被有效地抑制或消除就显得尤为重要，而对海杂波进行合理建模就是解决该问题的一个有效手段。

目前主流的海杂波建模方法主要有3类：第一类是散射机理的海杂波建模方法［1］，其依据形成海杂波的电磁散射原理来分析海杂波单元产生后向散射的原因，并在此基础上，运用海杂波雷达截面的相关理论，分析海杂波单元在不同海情下雷达散射截面所表现的特性。该杂波机理模型极其复杂且计算量巨大。第二类是统计分布的海杂波建模方法，其采用常用的统计模型（如对数正态分布模型、威布尔分布模型、瑞利分布模型）来模拟海杂波的统计特性，即把海杂波看作一个稳定的、无任何特性的随机过程，这种基于经验统计的研究手段大多数是出于数据的拟合和数学计算上的方便，忽视了海杂波形成的机理过程，很难表征出海杂波的内在动态特性。分形建模描述了海杂波的起伏程度，解释了海杂波的形成机理，弥补了统计模型建模的缺陷；其主要是通过提取出海杂波有效的分形参数，然后将参数输入到一个比较简单的迭代函数系统来仿真出一个雷达杂波信号，其模型的复杂度相对于散射机理模型大大降低了。

本文的建模方法在以往的加权组合多重分形模型上进行改进，将大量单一的分数布朗运动在概率意义上的线性组合改进为适量的复合布朗运动在概率意义上的线性组合，通过这种改进策略使得参与加权组合的分形信号的数量大大减少了，从而在确保达到以往加权组合模型仿真效果的基础上，减弱了模型的复杂度。

1 复合分式布朗运动

已有研究表明，复合的分式布朗运动是一个具有多重分型特性的随机过程。其主要是通过对一个单一分形的分式布朗运动随机采样得到的，在采样过程中为保证其仍具有长相关性，要求采样间隔不要过大。具体实现方法如下：

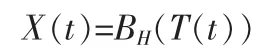
式中：BH（t）是一个经典的分式运动［2-5］。

2 相关分形维数

分形维数可以用来度量一个分形体的分形特性，是最重要的分形参数之一。分形维数的定义有很多种，就海杂波而言，不同海杂波的相关分形维数区别最大，即采用相关分形维数最能表征出海杂波的分形特性。因此，本文采用相关分形维数作为海杂波建模的输入参数。相关分形维数的估算方法很多，从计算的复杂度和精确度来考虑，采用基于算法的相关分形维数。下面对其进行简要介绍：

已知：时间序列X=｛x1，x2，…，xN｝

1）对X进行相空间重构，得到m维相空间Y=｛Y1，Y2，…，Ym｝

3）Cn（r）为各个相邻距离的对应点在所有的点中所占比，即：

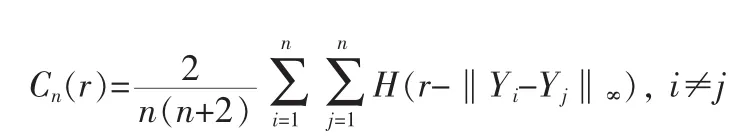
式中：H（·）为Heaviside单位函数，即：

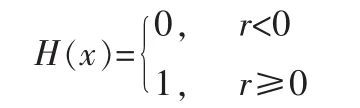
4）相关分维数D可以表示为

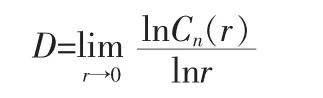
5）由相关分维数D可以计算出长程相关Hurst指数［6］

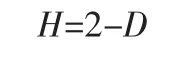
3 海杂波加权组合多重分形模型及仿真计算

3.1 海杂波加权组合多重分形模型

基于以上分析，可以将海杂波看作适量的复合布朗运动在概率意义上的线性组合，以下是加权组合模型的具体实现：

式中：

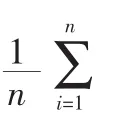
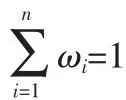
3.2 海杂波加权组合多重分形模型的仿真计算

仿真数据来自于加拿大McMaster大学对海进行探测实验所建立的Osborn Head Database［7］。具体采用典型的高海情海杂波数据hi.zip，其来自于第#269组纯海杂波数据，距离单元为3，HH极化。其数据已预经过处理，存储在纯ASCII文件中，数据中包含两列数据，其分别为I，Q两路数据，两路数据的长度均为2^17。根据I，Q两路数据求出其复接收量 hi，对hi求出幅度分量hiamp，取hiamp的前N=2^12个数据作为实验的数据X。

对实验数据进行初始化后，采用GP算法计算出X的关联分形维数，将关联分形维数作为建模的输入参数进行建模，具体的仿真流程如图1所示。

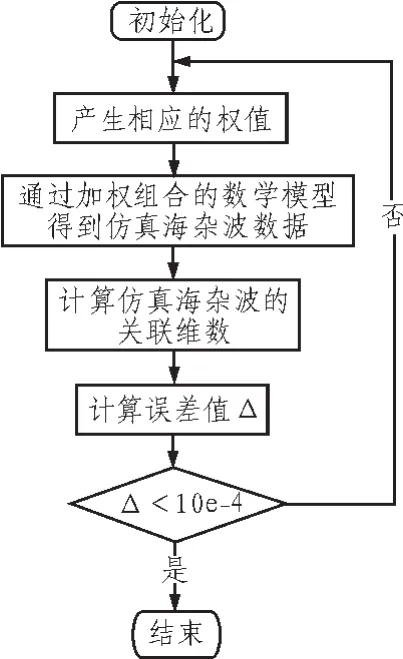
图1 仿真设计流程图Fig.1 Flow chart of the simulation design

3.2.1 高海清实测海杂波的建模多重分形特性仿真分析

图2给出了实测海杂波数据与本文多重分形模型仿真数据的质量指数τ（q）～q比较图，图中我们可以清晰地看出实测海杂波数据和本文多重分形模型的仿真数据的质量指数τ （q）与q均不呈线性关系，即τ（q）与q是相关的，基于多重分形的理论知识可以得出这样的结论：本文多重分形模型建模仿真出的海杂波数据具有多重分形特性，同时也说明了本文模型在多重分形特性的建模上的合理性。另外，由该图还可以看出τ（q）～q图形的形状吻合度较好，因此我们又能得到以下结论：实测海杂波数据与仿真海杂波数据的多重分形特性相似，即该模型在多重分形特性的建模上的精确度较高。

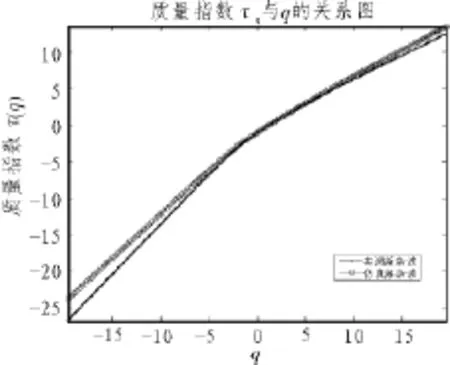
图2 质量指数τ（q）～q比较图Fig.2 Comparison chart the quality parameters τ（q）

3.2.2 高海清实测海杂波的建模复杂度分析

算法复杂度分为时间复杂度和空间复杂度。时间复杂度是执行算法所需要的计算工作量；空间复杂度是执行算法所需要的内存空间。由于海杂波建模所占用内存空间均较小，没有比较的意义，本文主要采用时间复杂度来度量模型的复杂度。

以往加权组合的海杂波多重分形模型与本文模型的算法时间复杂度的区别主要在于参与加权组合的分形信号的数量。由图3可见：在保证仿真数据的多重分形特性与实测海杂波数据的多重分形特性较为吻合的前提下，经过多次仿真实验可以发现，以往加权组合的海杂波多重分形模型大概需要参与加权组合的单一分形特性的粉丝布朗运动的数目为10 000左右，本文模型中参与加权组合的复合分式布朗运动数目为5 000左右。

4 结束语

本章讨论一种加权组合的海杂波多重分形建模方法，并采用公认的IPLX雷达典型的高海情实测海杂波进行建模与仿真。该模型仿真出的海杂波数据与模型输入源实测海杂波数据在多重分形特性较相似；并且在以往的加权组合多重分形模型上进行改进，大大减少了参与加权组合的分形信号的数量，在达到以往加权组合模型仿真效果的基础上，降低了模型的复杂度。另外，海杂波多重分形模型复杂度的降低使其更适用于目标检测领域［8-10］。

［1］Du G.Detection of sea-surface radar targets based on fractal mode［J］.Electronics Letters，2004，40（14）:906-907.

［2］Mandelbrot B B.The Fraetal Geometry of nature［M］.San Francisco:W.H Freeman，1982.

［3］Decreusefond L，stünel A S.Stochastic analysis of the fractional Brownian motion［R］.American Mathematical Society 1991 Subject Classifications，Primary 60H07；Secondary 60G18，2007:1-39.

［4］Kim T S，Kim S.Singularity spectra of fractional Brownian motions as a multi-fractal［J］.Chaos，Solitons and Fractals，2004，19（3）:613-619.

［5］Gao J B，Cao Y，Lee J M.Principal component analysis of 1/ fanoise［J］.Physics Letters A，2003，314（5/6）:392-400.

［6］Chang Yen-ching and Chang Shyang.A fast estimation algorithm on the Hurst parameter of discrete-time fractional Brownian motion［J］.IEEE Transactions on Signal Processing，2002，50（3）:554-559.

［7］Drosopoulos A.Description of the OHGR database［R］.Tech.Note No.94-14，Defence Research Establishment Ottawa，1994:1-30.

［8］陈小龙，刘宁波，宋杰，等.海杂波FRFT域分形特征判别及动目标检测方法［J］.电子与信息学报，2011，33（4）:823-830.［9］刘宁波，李晓俊，李秀友，等.基于分形自仿射预测的海杂波中目标检测［J］.现代雷达，2009，31（4）:43-50.

［10］HU Jing，TUNG Wen-wen，GAO Jian-bo.Detection of low observable targets within sea clutterby structure function based multifractal analysis［J］.IEEE Transactions on Antenna and Propagation，2006，54（1）:136-143.

Based on a weighted combination of sea clutter multi-fractal model

BAO Xing-xing
（Hohai University，Nanjing 210000，China）

A sea clutter multi-fractal modeling methods is designed in this paper，which is in order to improve the complexity of a weighted combination of past sea clutter multi-fractal model.The past sea clutter multi-fractal model is a linear combination of many fractional Brownian motions in the probabilistic sense.The complexity of the pat model depends primarily on two aspects:First，the model requires comparing the multi-fractal characteristics of input sea clutter and simulation sea clutter enough times to obtain the most similar simulation data in the modeling process；the second is to require a sufficient number of single fractal sequences to involve in a weighted combination，which is ensure the simulation output data has the similar multi-fractal characteristics of the input sea clutter.the model that is designed in this paper is still adopt the same method of the pat one，but it replace fractional Brownian motions with complex fractional Brownian motions to involve in weighted combination.The model that is designed in this paper make the best use of the advantage that complex fractional Brownian motions has the multi-fractal characteristics，which greatly reduces the number of participating weighted combination motions.so under the premise of reaching the best simulate sea clutter，the model that is designed in this paper greatly reduces the complexity of the past one.

weighted combination；multi-fractal；complex fractional Brownian motion；single fractal sequence；sea clutter

TN955

A

1674－6236（2016）04-0032-03

2015-03-28 稿件编号：201503407

鲍星星（1990—），女，江苏南通人，硕士研究生。研究方向：信号与信息处理。