带有非线性扰动的不确定时滞系统鲁棒预测控制

俞华军

（中海油气（泰州）石化有限公司 江苏 泰州 225321）

带有非线性扰动的不确定时滞系统鲁棒预测控制

俞华军

（中海油气（泰州）石化有限公司 江苏 泰州 225321）

针对一类具有非线性扰动不确定时滞系统，研究了使闭环系统渐近稳定且滚动时域性能指标在线最小化的鲁棒预测控制器设计问题。基于预测控制滚动优化原理，运用Lyapunov稳定性理论和线性不等式方法，将无穷时域“min-max”优化问题转化为凸优化问题，给出了系统稳定的充分条件。优化问题的可行性保证了算法的鲁棒稳定性。最后通过仿真验证所提方法的有效性。

鲁棒预测控制；非线性；不确定性；线性矩阵不等式（LMIs）；时滞

为了控制系统达到良好的跟踪性能，在每一采样时刻，通过滚动优化的方式实时处理控制量和状态量的约束问题，这就是预测控制的原理。工业过程控制中的模型、内部和外部扰动且不可避免。然而，MPC是一种基于对目标函数在有限时域内进行在线优化的算法，因此当控制系统存在模型不确定性，出现内部和外部扰动时，MPC的控制系统的温度性难得到保证［1］。

鲁棒预测控制是采用预测控制滚动优化思想处理模型的，使受控系统在满足可行性条件下达到渐近稳定的方法［2］。它能够有效处理模型不确定和扰动问题，弥补了经典预测控制设计没有考虑模型不确定性和扰动的不足［3］。目前，关于不确定时滞系统的鲁棒预测控制进行了大量的研究工作并取得了许多研究成果。文献［4］和文献［5］对时滞系统鲁棒预测控制进一步研究，该文献具有一定的保守性，主要由于是鲁棒预测控制在整个预测时域采用相同的状态反馈律，在考虑问题是不够全面，有一定局限性。在文献［5］的基础上，文献［6］是在状态和输入不确定时滞系统中用鲁棒预测控制滚动优化思想，将无穷时域优化问题通过近似求解，从而得到一种设计鲁棒预测控制器的可行方法。在实际工业过程控制中，各种时滞和扰动问题是普遍存在的，它们往往是导致系统不稳定。在上述文献中，都没有考虑非线性干扰对系统的影响。为此，本文在前人研究工作基础上，提出了一种适合于带有非线性扰动的不确定时滞系统的鲁棒预测控制方法，通过在每个采样周期在线求解无穷时域 “min-max”优化问题，运用Lyapunov稳定性理论和线性不等式方法，给出了状态反馈控制器存在的充分条件。在此基础上，分析闭环时滞系统的 渐近稳定性。最后通过仿真验证了所提出方法的可行性。

1　问题描述

考虑以下一类具有状态时滞及非线性干扰的不确定时滞系统

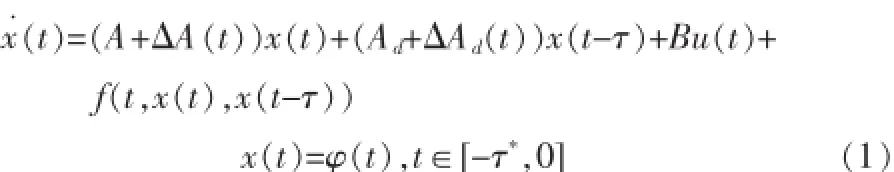
其中x（t）∈Rn，u（t）∈Rm分别表示系统的状态向量和输入向量，τ∈R+为未知有界时滞，满足 τ≤τ*，τ*为已知常数，φ（t）为可微的初值函数向量，A，Ad，B是适当维度的常矩阵，Δ（A），ΔAd（t）表示参数不确定性矩阵，并具有以下形式：

其中M，Ea，Ed为适当维度的常矩阵，F（t）∈Ri×j为未知的实值有界函数，且满足F（t）TF（t）≤I，f（x，x（t），x（t-τ））为有界非线性扰动，且满足有界条件：

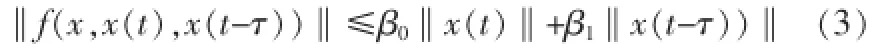
其中β0≥0，β1≥0为常数。对任意常数，。

对于系统（1），采用与文献［7］相类似的指标：

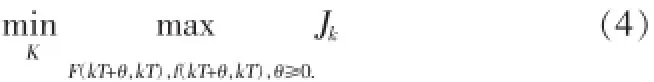
鲁棒预测控制融合对不确定性的处理方法和鲁棒控制滚动优化思想，在每一采样时刻实施控制作用。采用状态反馈控制结构如下：

在t∈［kT，（k+1）T］周期内实施状态反馈控制，通过以下闭环系统得到（k+1）T时刻的可测状态：

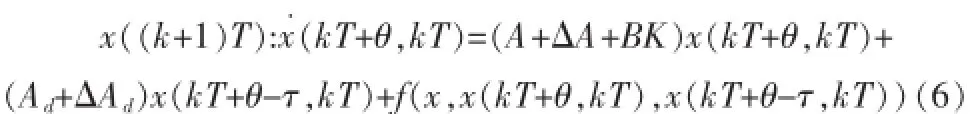
文中的主要是针对带有扰动不确定时滞系统（1），设计状态反馈鲁棒预测控制器，通过在每一采样时刻，求解优化问题（4），确定出一个状态反馈控制律，使得闭环系统在满足可行性条件下达到渐近稳定。

引理1设D、F、E为具有适当维数的实矩阵，且有F（x）F（t）T≤I，则对任意标量ε＞0，以下不等式成立：DFE+ETFTDT≤εDDT+ε-1EET。

引理2假设矩阵Y，D，E具有适当的维数，且Y是对称矩阵，则Y+DFE+ETFTDT＜0，对所有满足F（t）F（t）T≤I的矩阵F（t），当且仅当存在一个常数ε＞0，使得Y+εDDT+ε-1EET＜0。

2　鲁棒预测控制器设计

针对一个带有扰动不确定时滞系统（1），为了求解优化问题（4），选取以下Lyapunov函数：

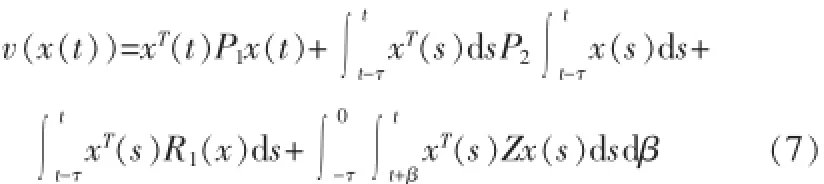
其中P1＞0，P2＞0，R1＞0，Z＞0在每一采样时刻kT，假设V（x （t））满足以下条件：

为保证性能指标（4）为有限值，假设 x（∞，kT）=0，那么V（x（∞，kT））=0。将式（8）从0到T积分，得：

并当T→∞时，由假设条件知xT（kT+T，kT）P1x（kT+T，kT）→0

由此可得：

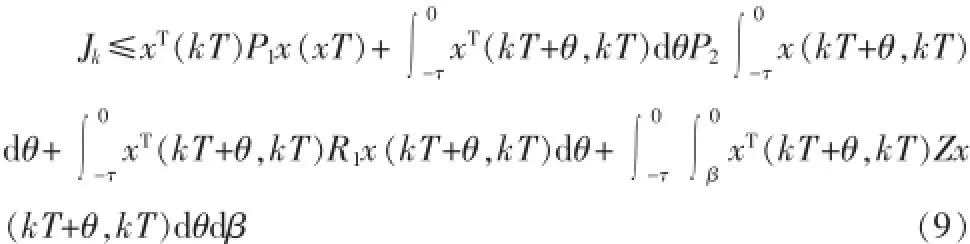
显然，V（x（kT））就是Jk的上确界。

定理 1对于具有扰动的不确定时滞系统（1）和性能指标（4），采用状态反馈控制律K=YX-1，使系统渐近稳定的充分条件是存在变量W0＞0，ε1、ε2＞0，及γ，X，X1，W0，W1，W2，W3，M1，M2，M3，Y满足以下形式的LMI优化问题：

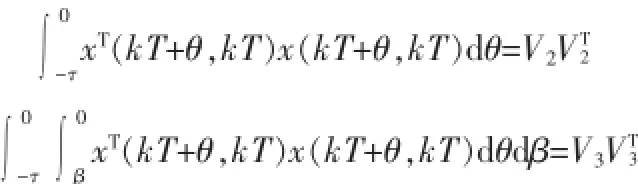
*代表相应的对称块矩阵

证明为了简化作如下定义：

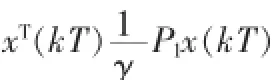
而二次型函数积分项式（9）的第一部分可转化为：

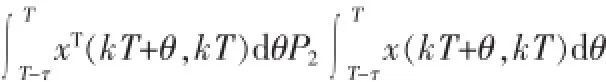
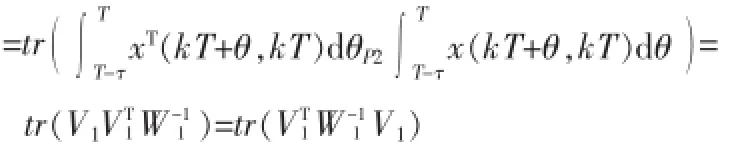
假设存在矩阵变量M1，满足tr（VT1W1-1V1）＜tr（M1），则根据Schur补定理得式（12）成立，其中P2=W1-1。同理可得二次型函数积分项式（9）的第二部分可转化为

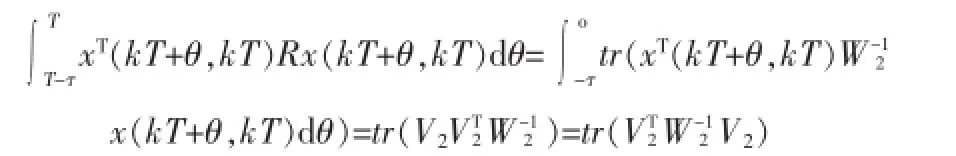
假设存在矩阵变量M2，满足tr（VT2W2-1V2）＜tr（M2）由Schu补定理得式（13）成立，其中R1=W2-1。同理假设存在M3，满足t （VT3W3-1V3）＜tr（M3）由Schur补定理得式（14）成立，其中z=W-13。从而可通过最小化γ+tr（M1）+tr（M2）+tr（M3）来保证式（9）给出的性能指标上界最小化。对式（7）求导并代入式（4），

并由式（3）和引理1，可将性能指标转化为：

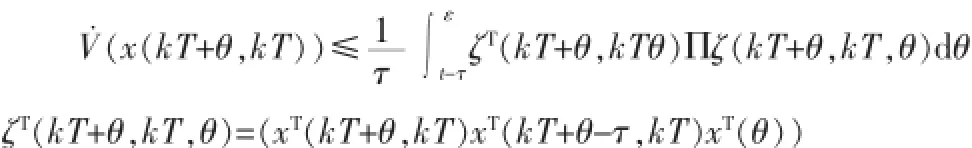
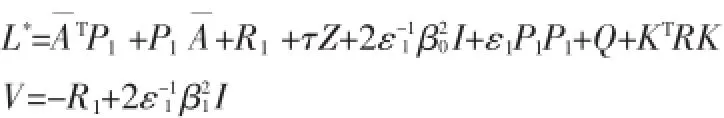
当时Π＜0，保证了V（x（kT））的单调递减性。由引理2知上式成立等价于存在一个常数ε2＞0，使得

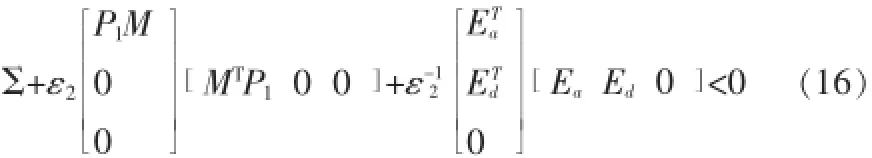
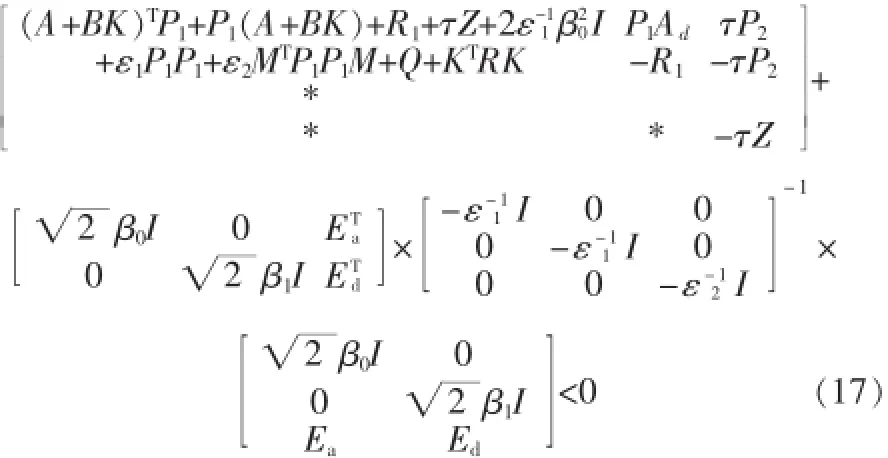
根据补定理，式 （17）可等价于线性矩阵不等式（18）：

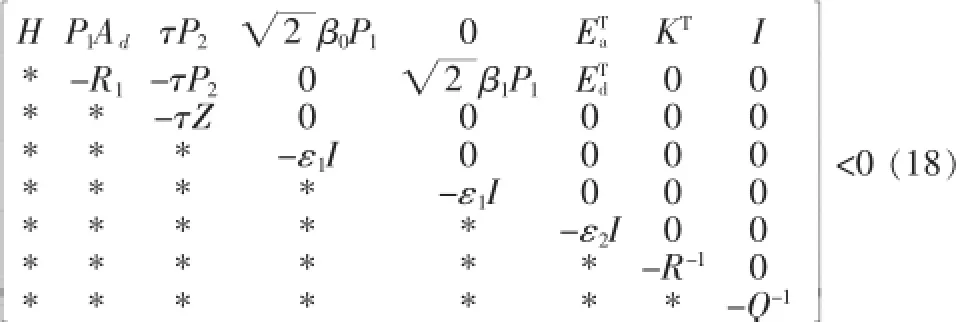
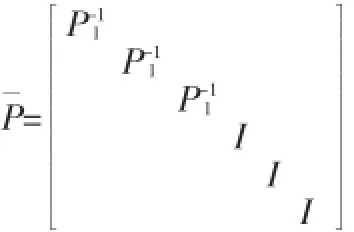
3　仿真实例

考虑不确定时滞系统（1），采用如下参数形式：

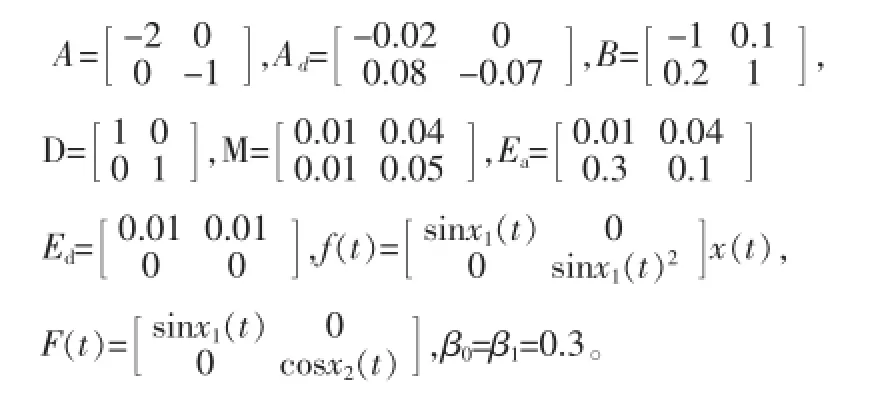
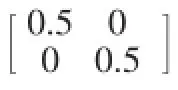
图1和图2分别为时滞无关鲁棒控制算法的状态响应曲线和控制作用曲线，图3和图4分别为基于状态反馈算法的状态响应曲线和控制作用曲线。从仿真结果可以看到，鲁棒控制算法处理非线性扰动时状态和控制作用都具有震荡和超调，而算法对非线性干扰有较好的抑制作用，明显优越于鲁棒控制算法，由图3和图4知，当时滞参数变化时，仍然具有较快的收敛速度。

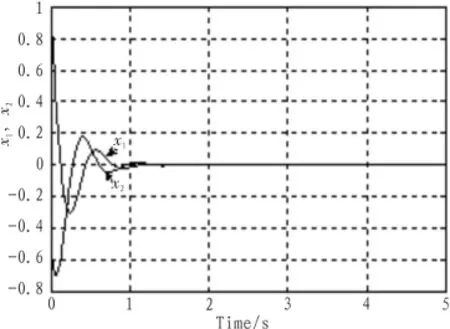
图1　系统状态响应曲线图

4　结　论

文中采用线性矩阵不等式方法，提出了具有非线性扰动不确定时滞系统算法。基于预测控制的滚动优化原理，通过在每个采样时刻在线求解相应的具有线性矩阵不等式约束的非线性规划问题，保证性能指标在线最小化。利用Lyapunov稳定性理论，证明了闭环系统是渐近稳定的。仿真实例验证了此方法的有效性。

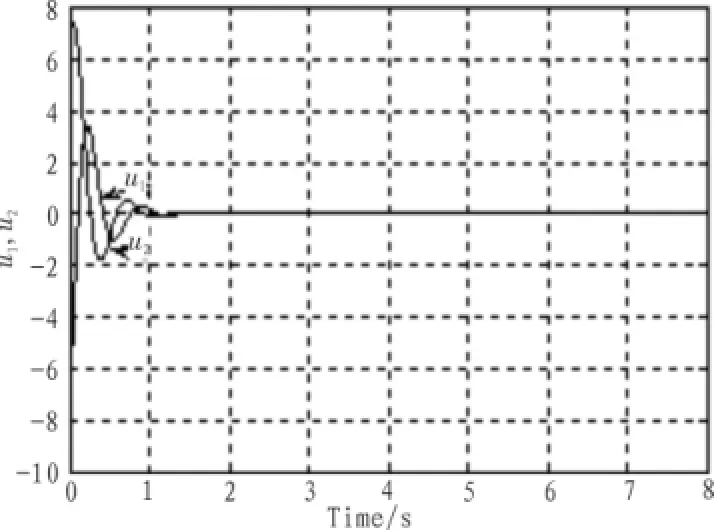
图2　控制输入曲线图

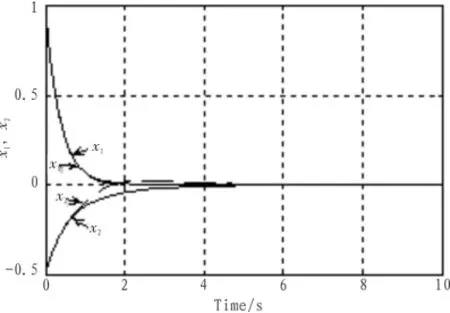
图3　系统状态响应曲线

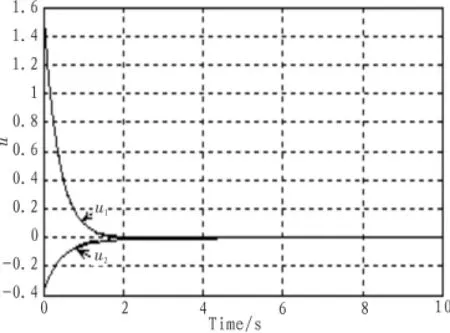
图4　控制输入曲线

［1］Chisci L，Rossiter J A，Zappa G.Systems with persistent disturbances：predictive control with restricted constraints［J］. Automatica，2001，37（7）：1019-1028.

［2］Ding B C，Xi Y G，Li S Y.A synthesis approach of on-line constrained robust model predictive control［J］.Automatica，2004，40（1）：163-167.

［3］Ding B，Huang B.Constrained robust model predictive control for time-delay systems with poly topic description［J］. International Journal of Control，2007，80（4）：509-22.

［4］陈秋霞，俞立.不确定离散时滞系统的输出反馈鲁棒预测控制［J］.控制理论与应用，2007，3（24）：401-406.

［5］Han C Y，Liu X H，Zang H S.Robust model predictive control for continuous uncertain systems with state delays［J］. Control Theory&Applications，2008，6（2）：189-194.

［6］刘晓华，王利杰.带有状态和输入时滞的不确定广义系统的鲁棒预测控制［J］.控制理论与应用，2010，4（27）：527-532.

［7］Wang Z D，Huang B，Unbehauen H.Robust reliable control for a class of uncertain nonlinear state-delayed systems［J］. Automatica，1999，35（12）：955-963.

Robust predictive control of uncertain time-delay systems with nonlinear disturbance

YU Hua-jun
（CNOOC（Taizhou）Petrochemical Co.，LTD，Taizhou 225321，China）

The design problem of robust state feedback model predictive controllers is considered which guarantees that the closed-loop system is asymptotically stable and an on-line receding horizon guaranteed cost is minimized for a class of uncertain time-delay systems with nonlinear disturbance.Based on predictive control principle of receding optimization，the infinite time domain"min-max"optimization problems are converted into convex programming problems by means of Lyapunov stable theory and linear matrix inequalities（LMIs）technique；and the sufficient conditions for the robust stability of the system are given.The feasibility of the above optimization problem guarantees the robust stability of the system.Finally，the simulation results illustrate the effectiveness of the proposed methods.

robust predictive control；nonlinear；uncertainty；Linear matrix inequalities（LMIs）；time-delay

TN495

A

1674－6236（2016）06-0190-04

2015-03-30稿件编号：201503447

俞华军（1983—），男，浙江绍兴人，硕士，助理工程师。研究方向：预测控制、非线性控制、汽轮机控制。