高中数学解题策略的思考*

☉江苏省盐城市第一中学 卢 敏

高中数学解题策略的思考*

☉江苏省盐城市第一中学 卢 敏

问题是数学的心脏，数学家存在的理由就是解题.因此，数学的真正组成总分就是问题和解；掌握数学就意味着善于解题.

什么是解题？解题就是一个人对问题所持有的看法.波利亚说过：所谓解题就是将我们要解决的问题转化为以往解决过的问题.他把解题分为四个步骤：（1）理清弄清题意；（2）拟定计划；（3）实施计划；（4）回顾问题.其中拟定计划就是解题的决策，也就是解题行动的总方针.下面我就通过几个问题谈一下解题行动的策略.

一、以退为进策略

华罗庚先生曾经指出：善于“退”，足够的“退”，退到最原始而又不失去重要性的地方，是学好数学的一个诀窍.从简单情况考虑，就是一种以退为进的一种解题策略.

例1 任给平面上5个点，记λ为5个点中任意两点间的距离的最大值与最小值之比.求证：λ≥2sin54°.

分析：1.λ实质是5个点中任意两点间的距离之比的最大值，即λ=

2 “.λ≥2sin54°”，只要存在一对距离之比≥2sin54°就足矣.关键是5点的任意性使我们连图都无法画出.

步骤1：退——退到简单的地方——5点共线，如图1所示.

图1

设A、B、C、D、E五个点共线，则任意两点间的最长距离=|AE|，最短距离=min｛|AB|，|BC|，|CD|，|DE|｝≤因此λ≥

=4＞2sin54°.此结论并非题目要求.题中要求λ≥2sin54°，而2sin54°＜2，因此，5点中只要有三点A、B、C共线，就可得证λ≥=2＞2sin54°.

步骤2：任意三点都不共线.此时，又是一个难点.5点位置应该怎样？找最简单的基本图形——正五边形的五个顶点，如图2，

图2

思考：上述问题的特征是“边”不定，唯一定的是“角”.结论是“=”，而问题是要“≥”，怎样放大？

步骤3：放大一个比值λ，可以放大分子，亦可以缩小分母.我们可以保持AB不动，拉长BE，如图3，

图3

步骤4：对任意三点都不共线的5点的分类：①若5点构成一个三角形ABC及其内部的两点D、E.如图4，此时∠ADB，∠BDC，∠CDA中最大角≥120°＞108°，问题得证.

图4

图5

②若5点构成一个凸四边形ABCD及内部一个点E，如图5，连接AC，则E必位于△ABC或△ACD内，由①知，必存在一个＞108°的角，问题得证

③若5点构成一个凸五边形，则其最大内角≥108°，问题得证.

以退为进策略，从最简单情形或者最特殊的情形开始思考，发现递推规律.对于一般情形成立的命题，考虑其特殊情形，一方面等于增加了一个条件，另一方面把复杂问题更加简单，从而易于问题的解决.

二、回归定义、概念的策略

解题贯彻于整个学科的学习和教学过程，要想解好数学题还必须学会程序化设计，要想更好地进行程序化设计，知道第一步该干什么，第二步该干什么，…，必须把那些陈述性知识的结构，以及蕴含在其中的一些运算规律，即算律也都弄清楚才行.越是一些平时不多见的、较难的题目，越应该回归原有的定义、公式，包括定义和公式的一些推导过程，即它们的来龙去脉都要回顾一番，看能否找到解题的蛛丝马迹，寻找突破口.

12P为椭圆在x轴的上方的定点，且满足kPF2=-4，试求S△PF1F2.

0繁，几乎到了你忍耐不了的地步.

图6

若用椭圆的焦半径公式：

|PF1|=a+ex0，|PF2|=a-ex0及构造直角三角形求出x0，进而很易得出y0：

评注：这道课本题目，如果用参考答案提示的方法，笔者曾经作过比对，所需时间是以上介绍方法所用时间的十多倍，这足以显现此法的优越性.

乔治·波利亚（George Polya）指出：“掌握数学意味着什么呢？这就是说善于解题，不仅善于解一些标准的题，而且要善于解一些独立思考、思路合理，见解独到和有发明创造的题.”能对陈题新解，难题妙解，繁题简解，大题小解.这种回归定义顺势而为的解法才更符合学生思维的最近发展区，学生才乐于接受.

三、等价转化策略

数学思维优秀者之所以能有效的解题，无论是其推理论证方法之美妙，还是其计算方法之灵巧，都在于有意识或无意识地利用了各种转化.这就是说：“他们往往不是对问题实行正面的攻击，而是不断地将它变形，转化问题的形式，从侧面或反面寻找突破口，直到把它转化成已经能够得到解决的问题.

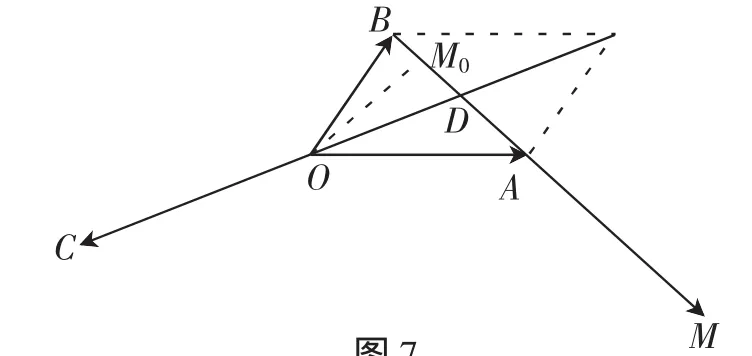
图7

信息“c与a-b所成的角为120°”说明：∠ADC=120°，从而∠ODM0=60°；

将给定的题设条件逐条转化也是解题常用的策略，上述每一个信息都进行转化，构成一个转化链，再借助于图形，最终解决问题.

四、整体思维策略

整体思维是求解数学问题常用的一种思维方法，可以有效地避免在细小的枝叶问题上的纠缠，从而达到简捷求解的目的.

例4 关于x的二次方程x2+z1x+z2+m=0中，z1，z2，m均是复数，且z-4z2=16+20i，设这个方程的两个根α，β满足|α-β|=2.求|m|的最大值和最小值.

所以（α-β）2=（α+β）2-4αβ=z-4z2-4m，

|α-β|2=|4m-（z-4z2）|=28，

这表明复数m在以A（4，5）为圆心、7为半径的圆周上，如图8所示.

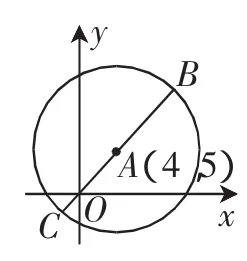
图8

连接OA，延长OA交⊙A于两点B与 C，则|m|的最大值为|OB|max=|OA|+|AB|=的最小值为|OC|min=|CA|-|AO|=7-

本题运用了整体代入的思想，有效地避免求两根的繁杂运算，根据题目条件直接建立等量关系.在求解数学问题时，如果能够找准思维起点，也就找到了解题的佳径，从而可以快速简捷地解题.

五、模型辨别策略

在平时的解题过程中，常常会有一些基本图形或基本题型，经常将一些复杂不熟悉的题目转化为熟悉的题型解决.

例5 已知x，y，z∈R+，且满足求 xy+2yz+3zx的值.

分析：条件是一个三元二次方程组，按常规求解非常困难，甚至无法完成，怎么办？观察形式，方程①，③类似于余弦定理结构，方程②是一个直角三角形的三边关系.

图9

【策略二】S△ABC=S△OAB+S△OBC+S△OAC.

则S△ABC=；而S△AOB=，化简可得：xy+2yz+3zx=24

（限于篇幅，具体解答略）

解决问题是一个亘古常青的课题，数学家在解决问题时考虑的角度各有不同，因此对问题的解决往往会有好多种方法.本文所谈的几种策略仅是冰山一角，只要教师长期坚持以一个研究型教师的标准要求自己，提升自己的专业素养，必能提高学生的解题能力，从而提高学生的学习境界和知识层次.

*本文为江苏省教研室2015年度第十一期课题“基于数学学习理论的高中数学教学设计研究”的研究成果.