室内行人航迹推算/超声波组合定位融合算法

赵延鹏，时伟，艾明曦

（中南大学 航空航天学院，湖南 长沙，410083）

室内行人航迹推算/超声波组合定位融合算法

赵延鹏，时伟，艾明曦

（中南大学 航空航天学院，湖南 长沙，410083）

为提高室内定位系统精度和跟踪性能以及适应复杂环境，将行人航迹推算与超声波定位组合，提出基于平方根无迹卡曼滤波的噪声权因子辅助协方差加权融合算法，并将全局最优融合状态作为反馈量引入算法。针对超声波对行人航向角测量困难，采用一种简单有效的几何方法。仿真结果表明：在模拟的室内动态环境中，包括在多路径效应和惯性累积误差的影响下，融合算法始终比单模型定位精度高，并有很好的收敛性、稳定性与适应性，对室内定位技术研究与应用具有重要意义。

室内定位；平方根无迹卡曼滤波；噪声权因子；协方差加权融合；航向角测量

近年来，人们对室内定位的需求日益增加，例如在城市高楼群、购物商场、火灾现场、医院病人监控等都需要基于个人位置的服务。因此，实现低成本且高精度的室内定位具有非常重要的现实意义。在空旷的室外地区，卫星导航定位系统可为用户提供可靠的位置信息；在复杂的室内环境，卫星信号因无法很好地穿透建筑物，不能提供准确的位置信息。为了弥补这一定位盲区，多种室内定位技术相继被提出，主要包括：行人基于自包含传感器的定位技术（传统惯性导航机制、行人航迹推算）、AGPS（Assistant-GPS）定位技术、无线定位技术（超声波、红外线、WLAN信号、射频无线标签、UWB等）、其他定位技术（麦克风阵列、电力线室内定位、地球磁场、计算机视觉识别等）［1-3］。基于行人航迹推算（pedestrian dead reckon，PDR）的定位技术具有导航定位自主性和连续性优势，但随着时间有累积误差缺陷；超声波定位具有结构简单、适应能力强、定位精度高等优势，但多路径效应较强［3-4］。为实现高精度、可靠的室内定位系统，本文作者把以上2种独立定位系统组合，利用多种信息源，互相补充，构成一种有多余度和精度更高的多功能PDR/超声波组合定位系统。融合算法作为组合导航定位的关键技术，已成为当前研究热点。目前，国内外学者对卫星导航和惯性导航系统的融合算法做了大量研究，而针对室内组合定位系统的融合算法所做的相关研究较少。基于 Kalman滤波的信息融合技术是当前研究的主要方向，本文室内组合定位系统状态方程为非线性，这给滤波器的设计带来了一定的困难。针对该问题，部分学者在工作点处做线性化后，采用扩展卡尔曼滤波（简称KF）进行状态估计，EKF的线性化误差会降低模型的准确性，随着时间延长，估计精度难以保证。另外EKF在滤波前必须计算非线性模型的Jacobian矩阵，这一过程非常繁琐且极容易出错［5］。自无迹卡曼滤波（简称UKF）被提出来后，其应用领域不断扩展，UKF与EKF相比，能更准确地估计状态及其方差，无需对非线性状态函数和观测函数求导，具有收敛速度快、估计精度高和易于实现的优点［6-7］。但是 UKF会由于计算误差和噪声信号等因素引起误差协方差矩阵负定，从而导致滤波发散。平方根UKF（简称SRUKF）算法以估计误差的平方根矩阵进行迭代计算，解决了常规UKF算法中滤波结果发散问题，提高了滤波精度和稳定性［8］。本文作者将SRUKF算法与协方差加权融合相结合应用于PDR/超声波室内组合定位系统，根据2种模型的系统噪声设置噪声权因子辅助协方差加权，有效地解决了针对室内动态环境的实时融合。同时，为了提高系统的跟踪性与稳定性，算法引入反馈机制。通过仿真实验，验证算法的融合效果，并对其进行分析比较。

1 室内定位方案

对于室内行人定位来说，正常情况下，行人是平稳地行走且高度方向上变化较小，因此被认为滚转角和俯仰角接近零，忽略高度通道。本文仅考虑行人航向角φ（本体系X轴与正北方向夹角，逆时针为正）、平面二维位置分量与速度分量。

1.1 行人航迹推算

目前，基于传统惯性导航机制和基于行人航迹推算的定位技术取得了一定成果［4，9-13］。

行人航迹推算在已知当前时刻位置条件下，利用惯性测量单元（简称 IMU）推算出下一时刻的行人位置，具有完全自主性，不受外界影响，数据更新速度快等特点。航迹推算算法的定位精度取决于初始位置和姿态信息的精确性以及推算过程中速度的航向信息求解。初始位置在实际应用中一般通过在室外由GPS等导航卫星定位获得，在本文仿真研究中将初始位置设置为坐标原点。姿态信息仅包括航向角 φ，可由陀螺仪与磁罗盘获得数据，用零角速率更新（简称ZARU）、滤波融合等算法解算获得。速度信息是行人航迹推算中主要研究热点，主要包括步态检测即人体步长估计模型以及步频检测。为了估计步长 L，目前存在的模型主要包括：常数/伪常数步长模型、线性步长模型、非线性步长模型和人工智能步长模型。最新研究表明加速度计或其他IMU固定在人体脚踝部位，步频探测效果最佳，利用零速更新策略（简称 ZUPT）估计误差并进行补偿获得步频f信息，降低位置发散速度，从而得到1个周期T内行人步数C=1/f。得到以上参数后通过航迹推算算法。

航迹长度为

得到当前时刻位置信息为

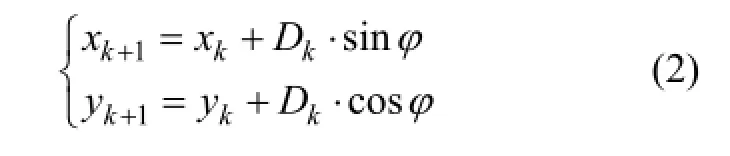
行人航迹推算模型图如图1所示。

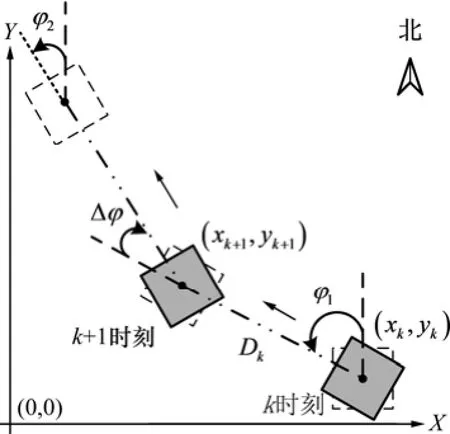
图1 行人航迹推算模型图Fig.1 Model of pedestrian dead reckon

1.2 超声波传感器定位

超声波作为一种非接触的检测方式，与红外、激光及无线电测距相比，不受光线、被测对象颜色等影响，在恶劣环境中具有一定的适应能力，比激光测距更容易获得近距离的信息，并且具有结构简单，成本低廉，精度高等优点。超声波测距原理是利用渡越时间法（time of flight，TOF），即检测超声波往返的时间，所用时间与超声波通过距离成正比获得超声波所经过的距离，常常用于导航定位［3，14］。

室内超声波定位系统中超声波传感器网络布置为：在穿戴于行人后背的定位装置上安装2个超声波发射器Ut1和Ut2，在天花板上按简单行列规律固定安装若干个全向超声波接收器Ur1～Urn。

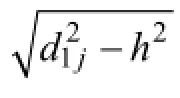
若有n个超声波接收器接收到Ut1所发射的超声波，由极大似然估计可构成如下方程组：

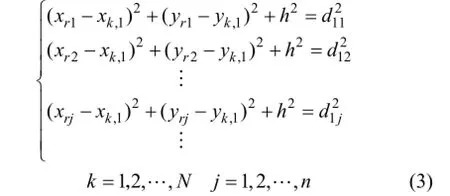
将上式方程组从第一个方程组开始依次与最后一个方程相减得

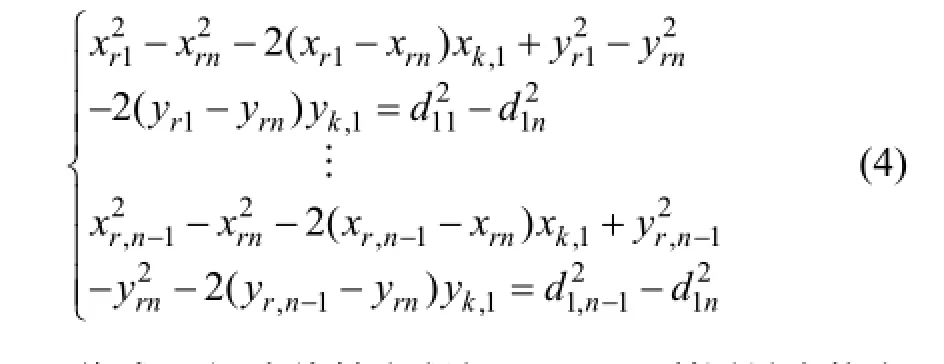
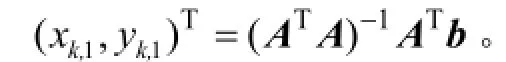
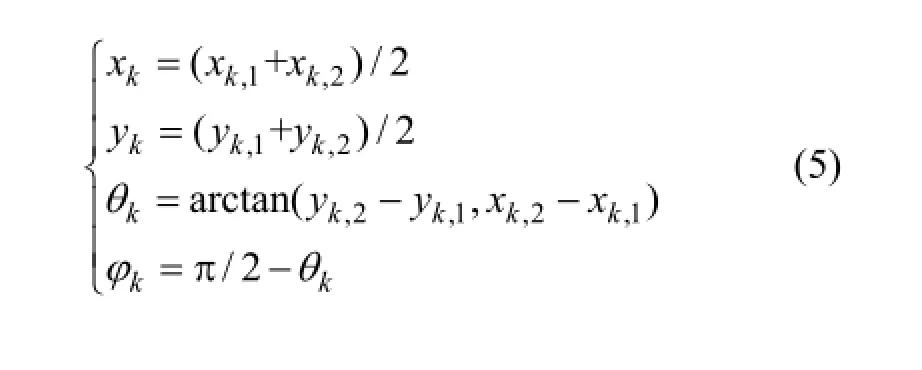
图2 穿戴式设备超声波定位模型图Fig.2 Model of ultrasonic position with wearable device

1.3 建立模型集

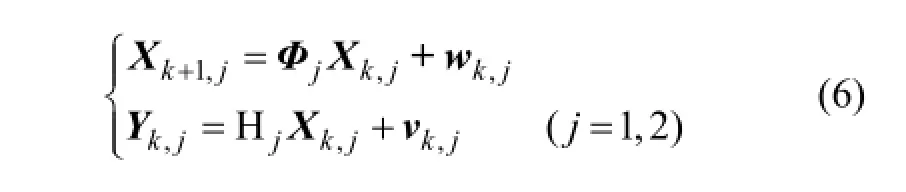
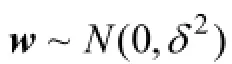
其中Q和R两者不相关。

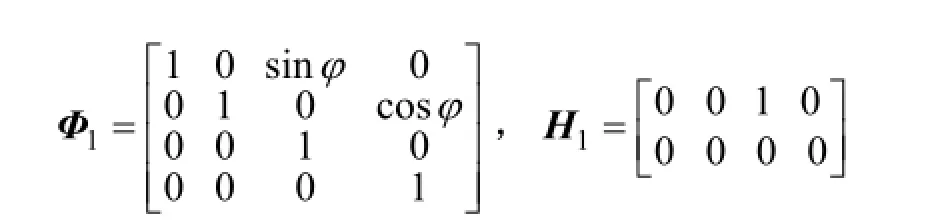
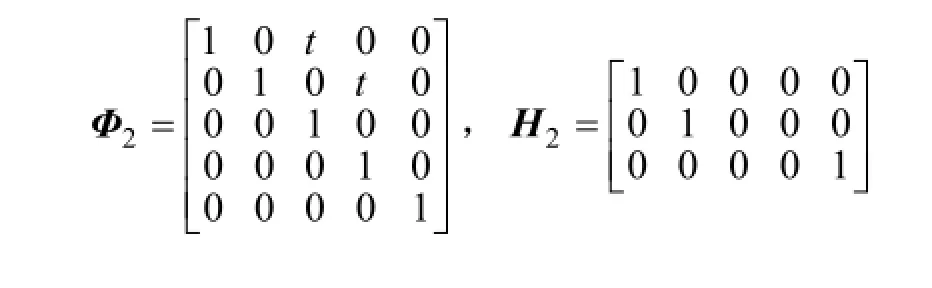
2 数据融合定位

2.1 SRUKF滤波算法

2.1.1 平方根U变换

U变换的主要思想是“近似概率分布要比近似线性函数更容易”，它通过设置 Sigma采样点和相应权值，逼近样本非线性变换参量的一阶矩和二阶矩。考虑1个L维随机变量x经过非线性变换后得到y=g（x），并假设x的均值和方差分别为和Px， x的Sigma样点｛χi｝和权值｛Wi｝可由和 Px得到。利用这些采样点通过非线性变换得到新的Sigma采样点集合［15］。

计算变量y的均值和方差为

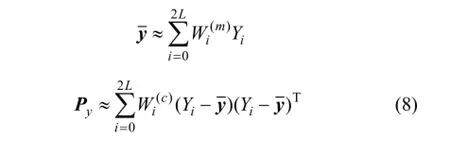
P通常为非负定矩阵，然而在滤波的迭代过程中，由于计算误差等因素的影响，致使滤波协方差不对称或负定，从而导致滤波发散，影响滤波算法的收敛性和稳定性。因此，将Py分解为

可以通过 Cholesky分解来得到Py的平方根矩阵S，而它在滤波更新算法中的导出可通过QR分解来实现。通过设定缩放参数，保证粒子权值为正，可得

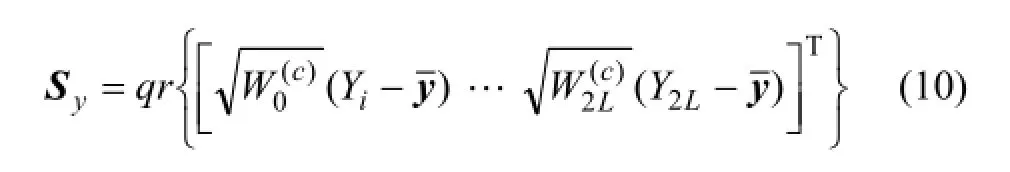
其中：qr表示得到QR分解中的R矩阵的函数。通过使用QR 分解，可以不必先求出样点的加权方差，再进行Cholesky分解，即保证了数值的稳定性，又减小了计算量。

在滤波过程中，用 Sy代替 Py参加递推运算可以保证协方差阵的非负定性，从而实现有效滤波。

2.1.2 算法步骤

UKF会由于计算误差和噪声信号等因素引起误差协方差矩阵负定，导致滤波结果发散。SRUKF算法以估计误差的平方根矩阵进行迭代计算，解决了常规UKF算法中滤波结果发散的问题，提高了滤波的精度和稳定性［5，16-17］。SRUKF滤波算法具体流程如下：

1） 初始化：

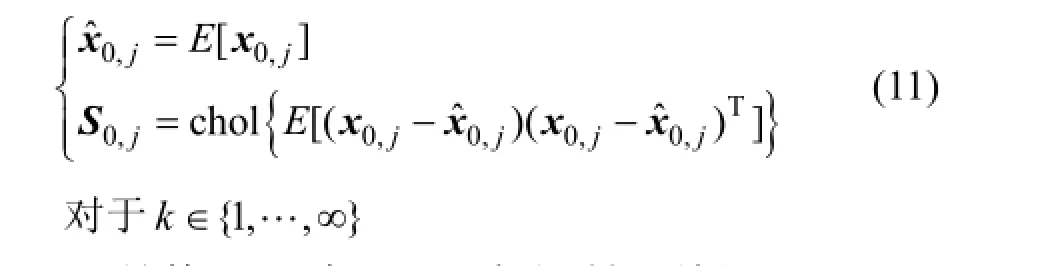
2） 计算2n+1个Sigma点和时间更新：

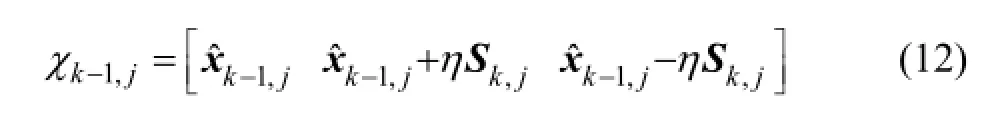
对每个Sigma点进行f（•）非线性变换：

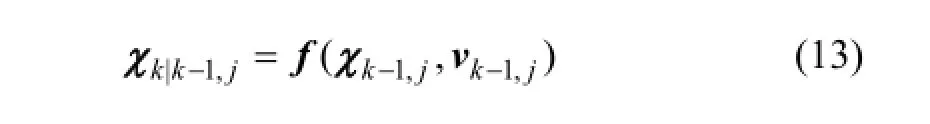
对变换后的Sigma点集进行加权处理，从而得到一步预测状态：

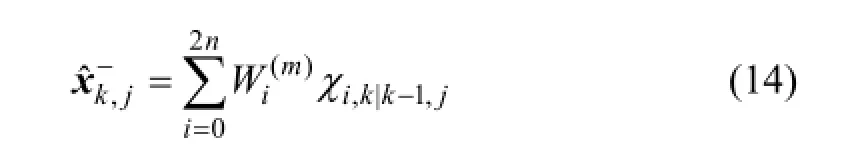
一步预测方差阵为

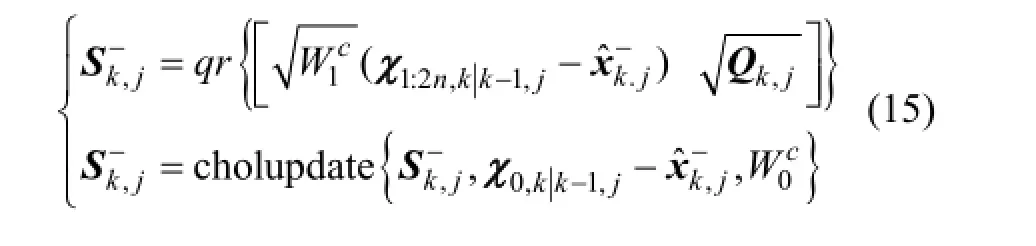
3） 测量更新：

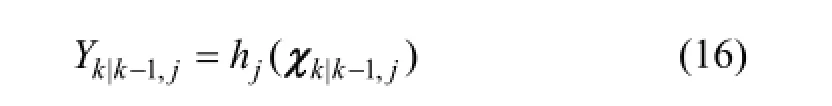
预测观测值为

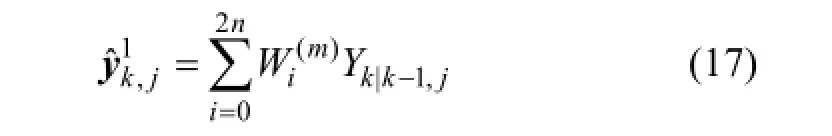
计算协方差为

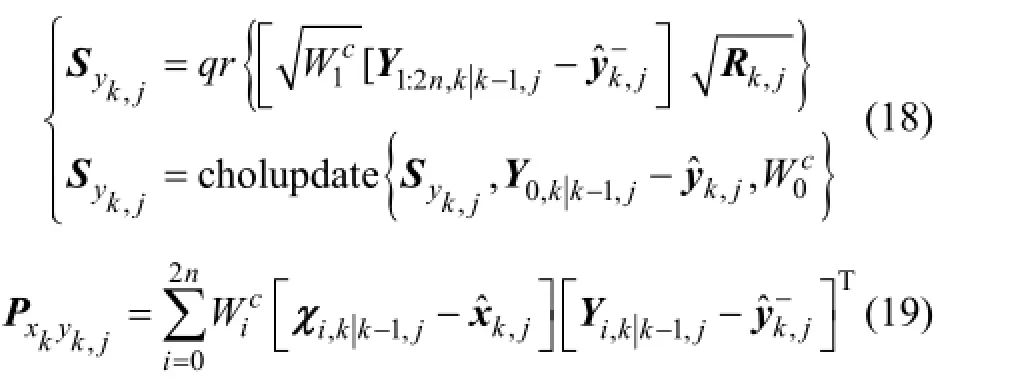
计算滤波增益为

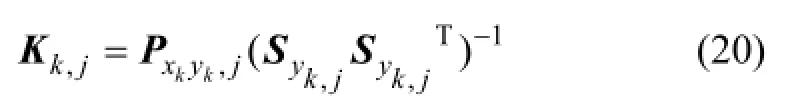
状态更新后的滤波值为

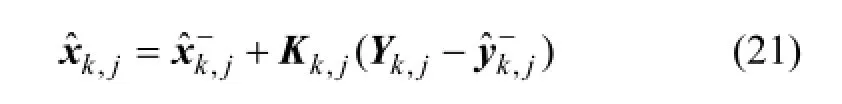
状态后验方差阵为

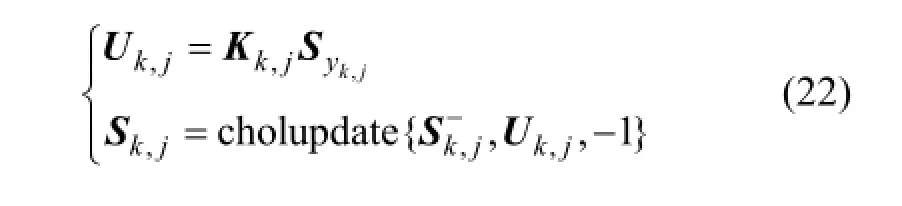
权重Wi为

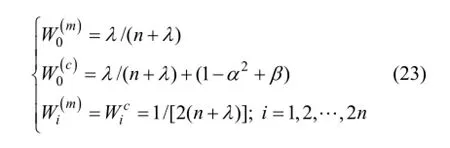
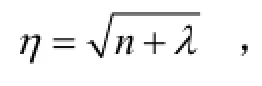
2.2 融合算法

在室内组合导航系统中，考虑到由于室内复杂未知环境的影响，比如室内物品遮挡造成的多路径效应、惯性器件的累积误差，造成个别模型或传感器受到干扰或失去对行人目标的覆盖。然而，本文研究方案中 PDR/超声波组合定位使两模型同时工作，如上文介绍 PDR和超声波定位方案可独立的获得定位信息，系统充分利用各传感器的测量值，通过数据融合进一步提高定位质量，能得到足够的目标信息，从而使系统的可靠性增强，信息置信度提高，时空覆盖区域扩大，减少了测量数据的模糊性，改进了系统的监测性能［18-19］。

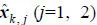
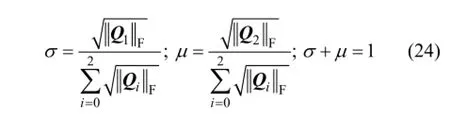
针对室内动态环境，通过噪声权因子σ和μ辅助协方差加权，以满足系统的实时融合效果。同时，为提高系统的跟踪性与稳定性，将上一时刻的全局最优估计融合状态作为反馈量引入算法。

基于以上分析，本文提出了基于SRUKF的噪声权因子辅助协方差加权融合算法，原理如图3所示。

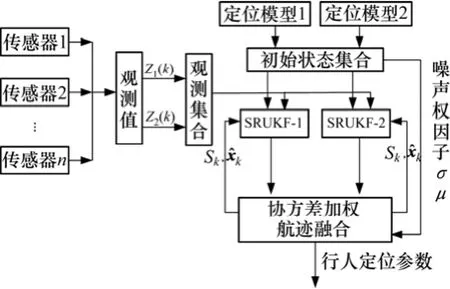
图3 基于SRUKF的噪声权因子辅助协方差加权融合算法框图Fig.3 Diagram of noise power factors assisting covariance weighted based on SRUKF

下面介绍噪声权因子辅助协方差加权融合算法具体步骤与策略：

2组定位模型k时刻最优航迹状态估计值之差为

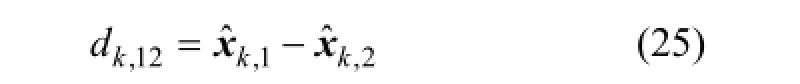
则d12，k的协方差矩阵为

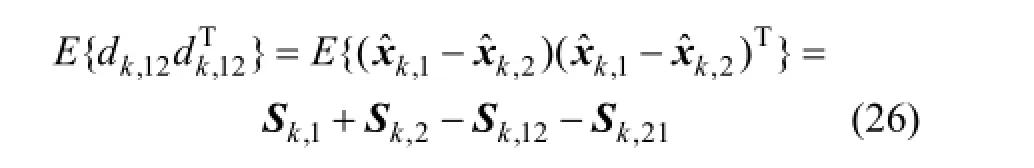
当采用SRUKF滤波器对定位模型进行状态估计时，互协方差S，12k可由下式求出：

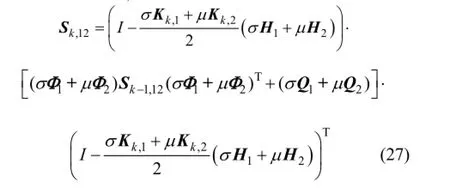
其中：Kjk，（j=1， 2）为SRUKF滤波器增益；Φ为状态转移矩阵；Q为系统过程噪声方差矩阵；H为观测矩阵；σ和μ为噪声权因子。

融合系统最优状态估计为

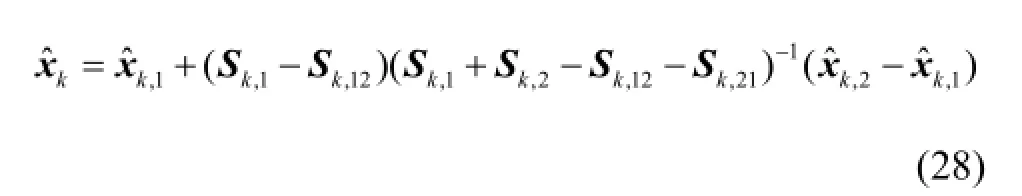
融合系统误差协方差为

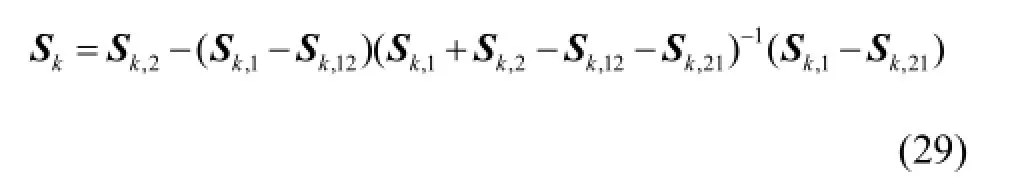
通过上述分析，可得到噪声权因子辅助协方差加权融合算法策略如图4所示。

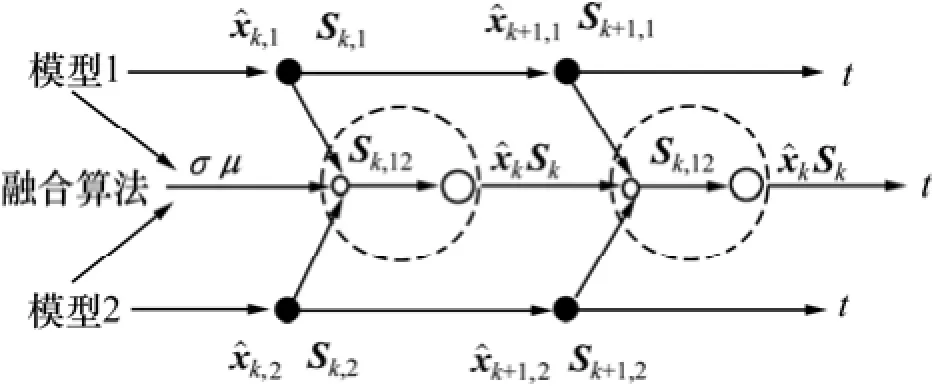
图4 噪声权因子辅助协方差加权融合算法策略Fig.4 strategy of noise power factors assisting covariance weighted

3 仿真实验与分析

为计算方便，本文统一将定位参数的采样周期 T设置为1 s，取α=0.001，κ=0，β=2。为了保证组合定位系统融合精度并控制滤波计算量，仿真时长为 120 s，采用Monte Carlo作M=600次仿真，同时为了验证算法的有效性，使用均方根误差（RMSE）作为行人跟踪性能指标。

仿真环境：行人初始位置为原点（单位： m），初速度为1 m/s，做近似匀速运动，初始航向角为20°。PDR定位系统采用荷兰Xsens公司生产的MTi微惯性航姿系统，其性能指标［22］见表 1。通过在地面上选取若干点，测量其至参考点的实际距离，再从定位系统中提取用超声波测量的距离，两者比较可得超声波定位系统的误差指标见表 1。系统所有误差均视为零均值高斯白噪声。

表1 PDR/超声波组合定位系统仿真参数设置Table 1 Setting simulation parameters of PDR/Ultrasonic

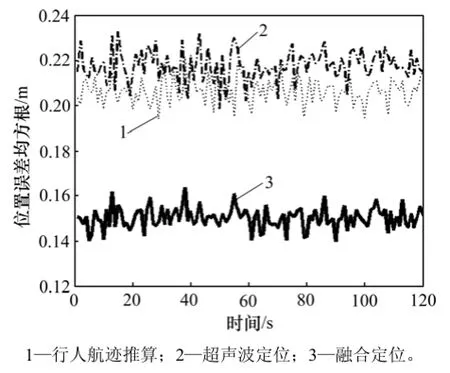
图5 融合算法与单模型的位置误差均方根Fig.5 RMSE of location with fusion algorithm and single model

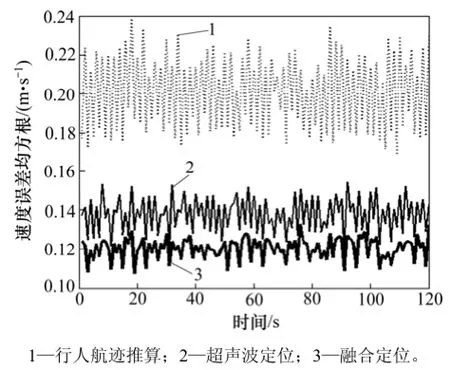
图6 融合算法与单模型的速度误差均方根Fig.6 RMSE of velocity with fusion algorithm and single model

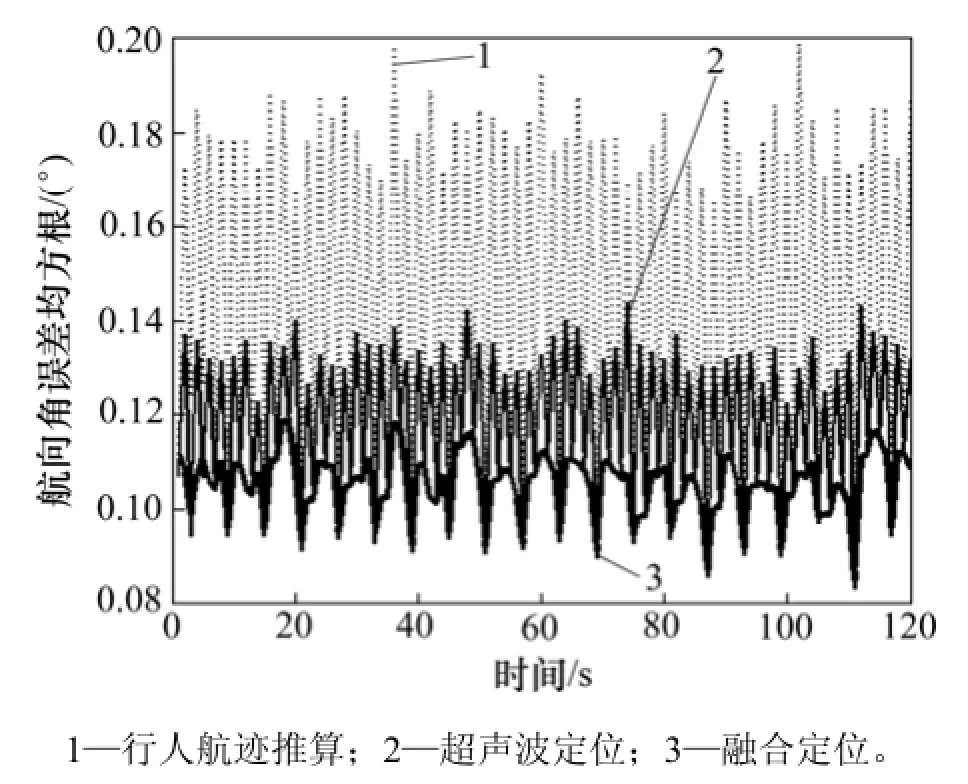
图7 融合算法与单模型的航向角误差均方根Fig.7 RMSE of course angle with fusion algorithm and single model

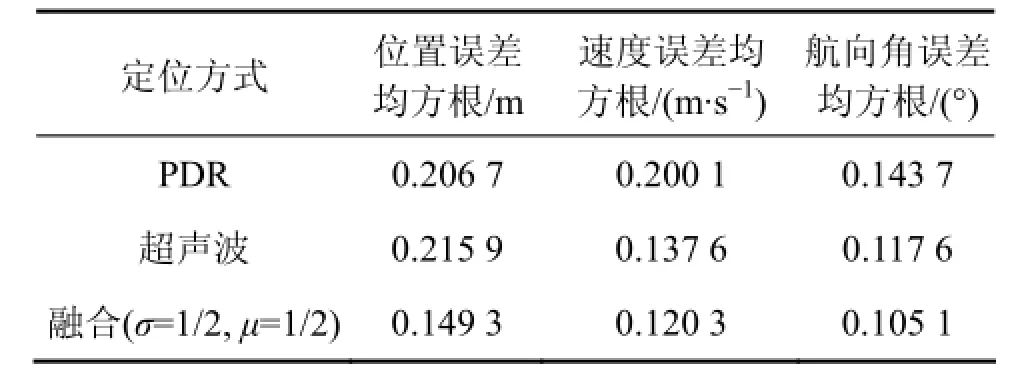
表2 无累积误差以及多路径环境下的误差均方根Table 2 RMSE without cumulative error and multipath effect

在 PDR与超声波定位系统各传感器测量精度一定的情况下，从仿真结果来看，当惯性累积误差以及多路径效应不明显时，PDR与超声波单模型定位方案均具有较高的定位精度且误差收敛在一定范围内，融合算法的定位性能高于单模型，与PDR和超声波定位相比，位置（x，y）定位精度分别提高27.77%和30.85%，精度＜0.15 m；速度v精度分别提高39.88%和12.57%，精度＜0.12 m/s；航向角 φ精度分别提高 26.86%和10.63%，精度＜0.11°。

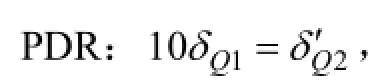
融合效果与实验1中误差均方根相比较，结果见表4。

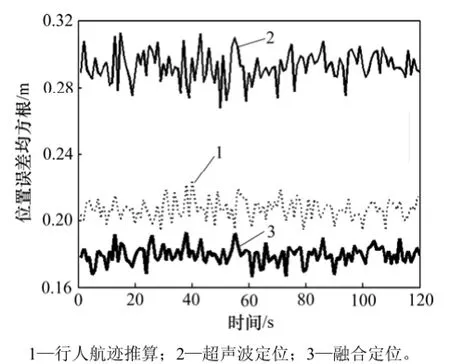
图8 融合算法与单模型的位置误差均方根Fig.8 RMSE of location with fusion algorithm and single model

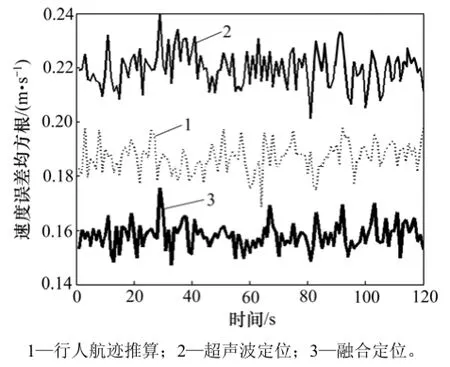
图9 融合算法与单模型的速度误差均方根Fig.9 RMSE of velocity with fusion algorithm and single model

图10 融合算法与单模型的航向角误差均方根Fig.10 RMSE of course angle with fusion algorithm and single model

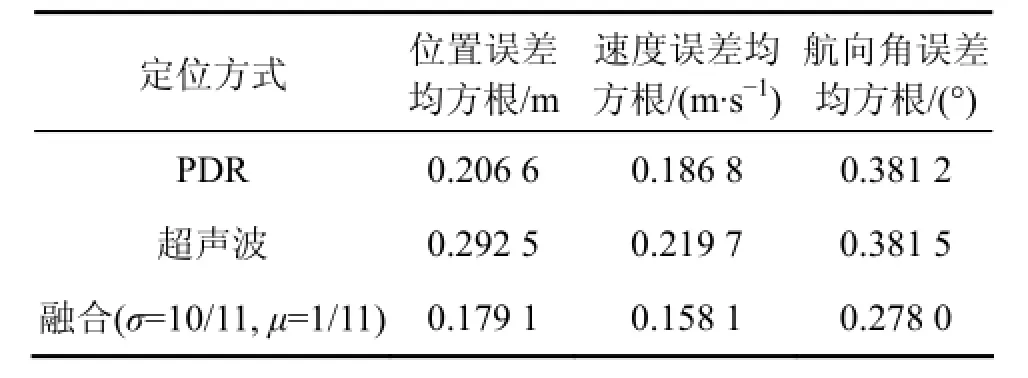
表3 无累积误差以及有多路径环境下的误差均方根Table 3 RMSE without cumulative error but multipath effect

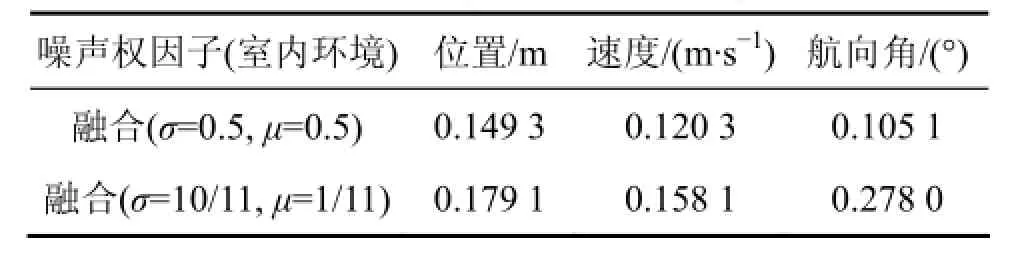
表4 实验1与实验2误差均方根对比Table 4 RMSE of experiment 1 and experiment 2

在 PDR与超声波定位系统各传感器测量精度一定的情况下，从仿真结果来看，PDR、超声波单模型方案定位误差均收敛在一定范围内，由于多路径效应影响了超声波定位，使得PDR定位精度高于超声波定位。融合算法的定位性能明显高于单模型，与PDR、超声波定位相比，位置（x， y）定位精度分别提升13.35%和38.77%；速度v精度分别提升15.36%和28.04%；航向角φ精度分别提升27.07%和27.13%。如表4所示，尽管室内多路径效应明显，整体融合效果相比于实验1略有下降，但定位参数精度仍较高，定位精度＜0.18 m，速度v精度＜0.16 m/s，航向角φ精度＜0.28°。

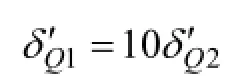
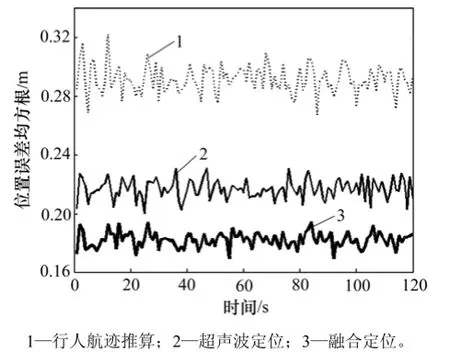
图11 融合算法与单模型的位置误差均方根Fig.11 RMSE of location with fusion algorithm and single model

图12 融合算法与单模型的速度误差均方根Fig.12 RMSE of velocity with fusion algorithm and single model

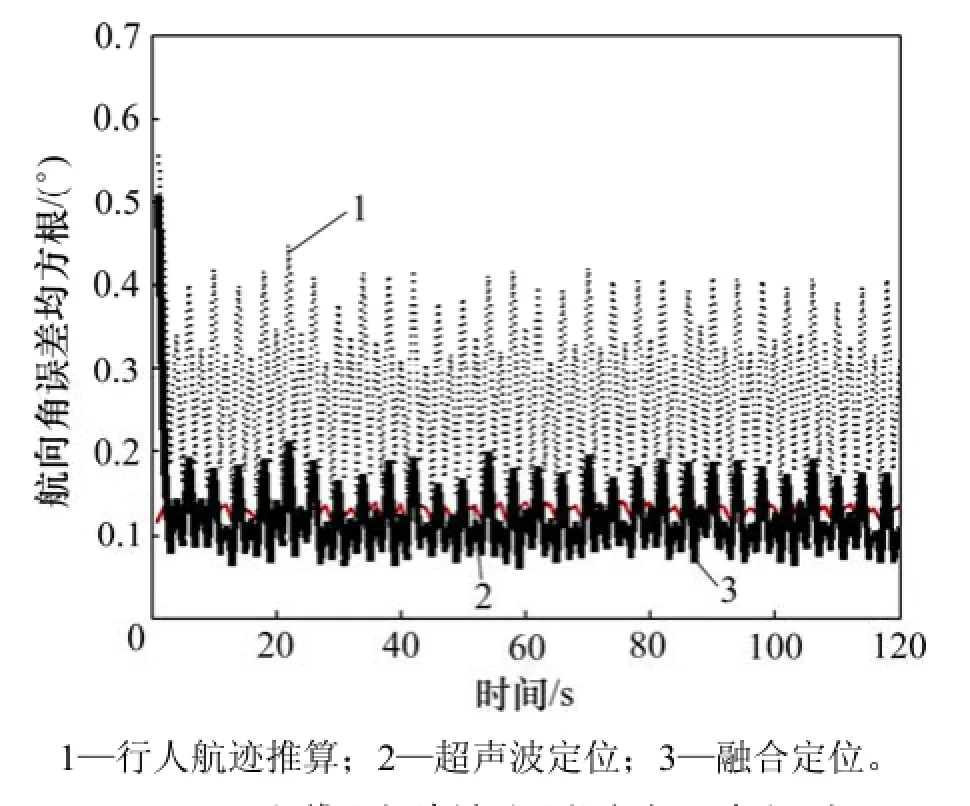
图13 融合算法与单模型的航向角误差均方根Fig.13 RMSE of course angle with fusion algorithm and single model

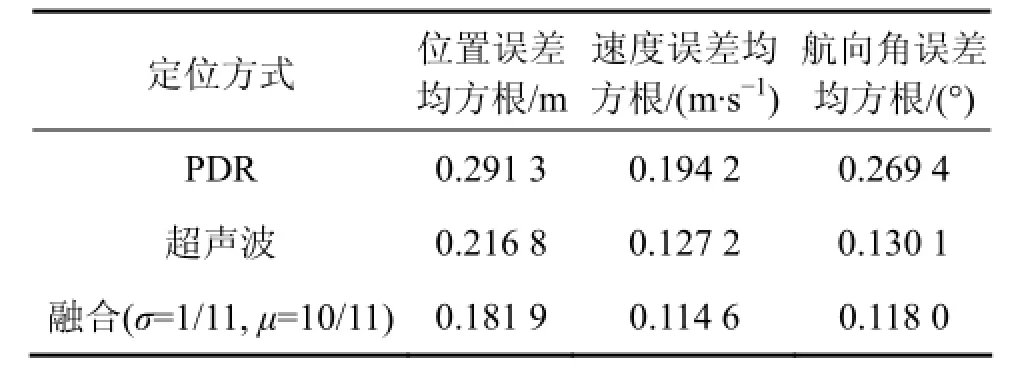
表5 有累积误差以及无多路径环境下的误差均方根Table 5 RMSE with cumulative error but multipath effect

融合效果与实验1中误差均方根相比较，结果见表6。

在 PDR与超声波定位系统各传感器测量精度一定的情况下，从仿真结果来看，PDR与超声波单模型方案定位误差均收敛在一定范围内，由于惯性器件的累积误差影响了PDR定位，使得超声波定位精度高于PDR。融合算法的定位性能明显高于单模型，与PDR、超声波定位相比，位置（x， y）定位精度分别提高37.56%和16.10%；速度v精度分别提高41.00%和9.91%；航向角φ精度分别提高56.20%和9.3%。如表6所示，尽管由于系统长时间运行，造成惯性器件累积误差明显，整体融合效果相比于实验1略有下降，但定位参数精度仍较高，定位精度＜0.19 m，速度v精度＜0.13 m/s，航向角φ精度＜0.12°。

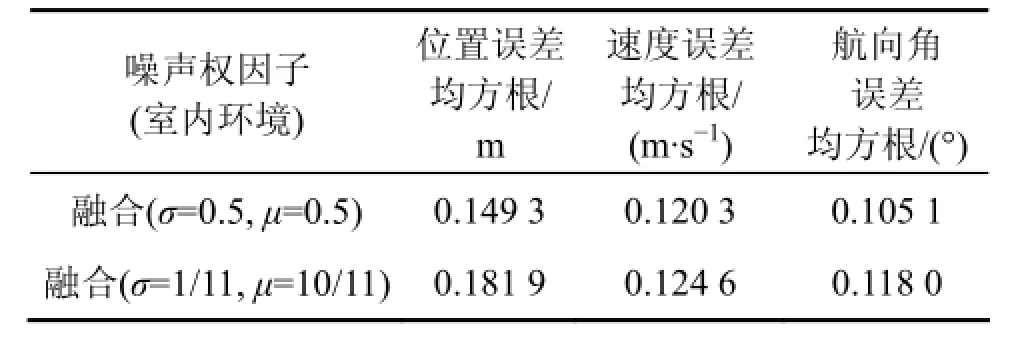
表6 实验1与实验3误差均方根对比Table 6 RMSE of experiment 1 and experiment 3

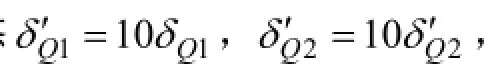
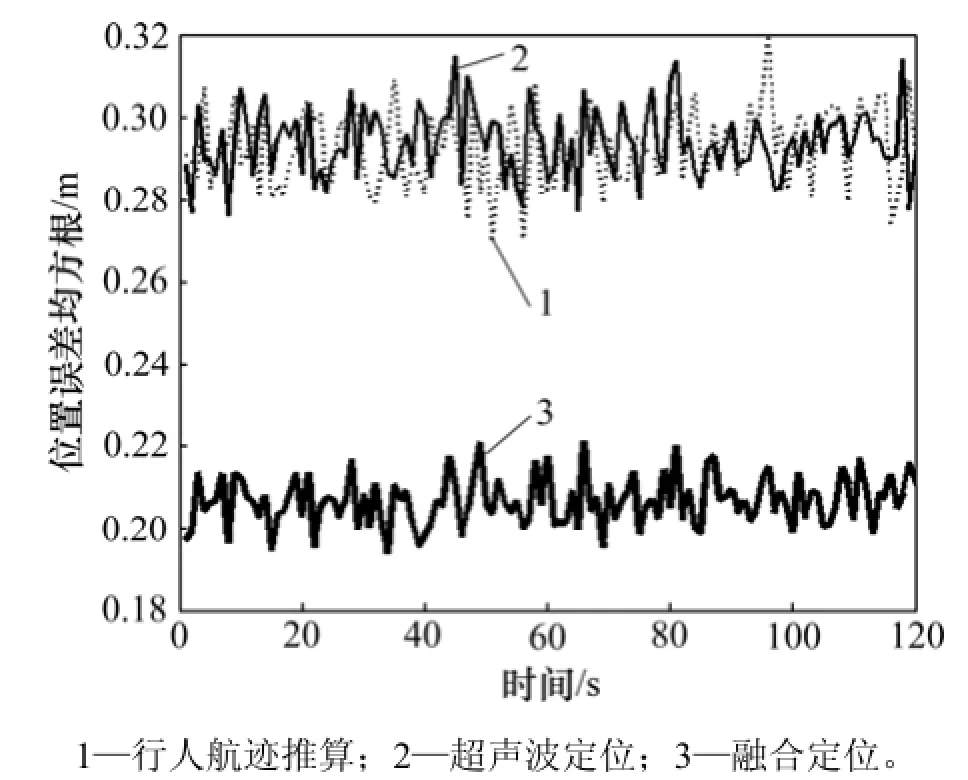
图14 融合算法与单模型的位置误差均方根Fig.14 RMSE of location with fusion algorithm and single model

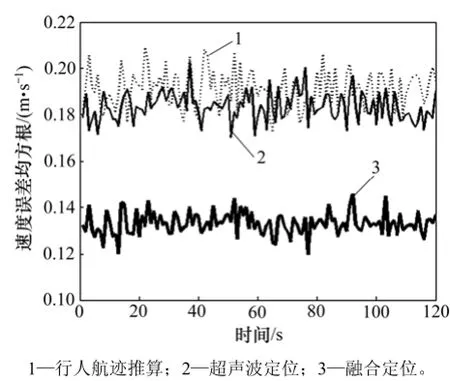
图15 融合算法与单模型的速度误差均方根Fig.15 RMSE of velocity with fusion algorithm and single model

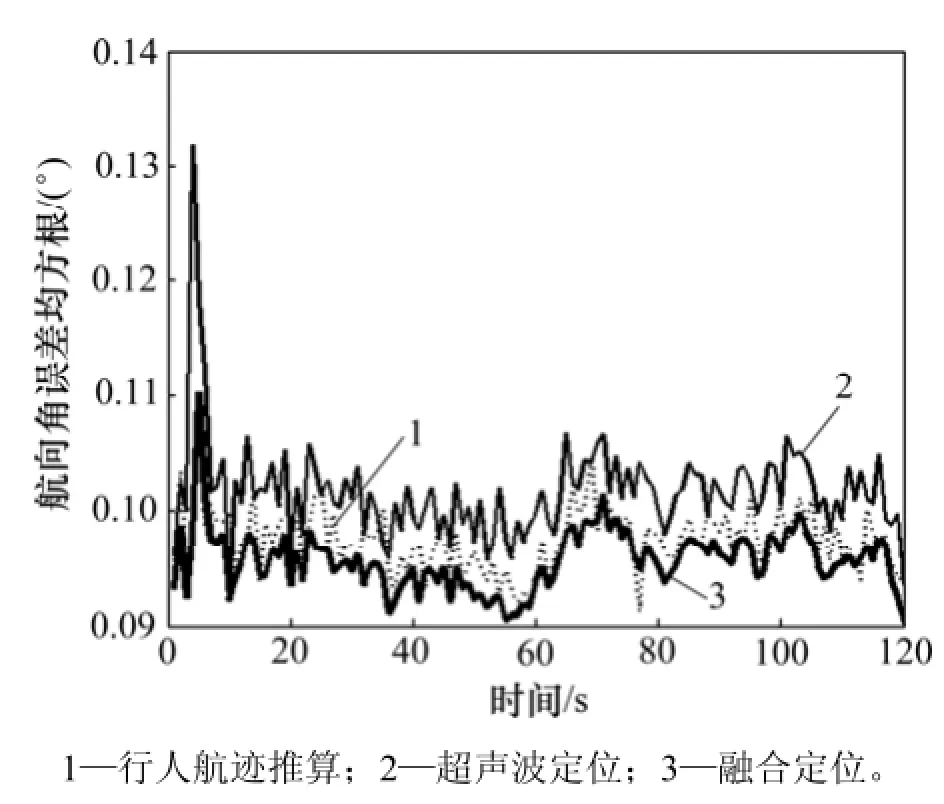
图16 融合算法与单模型的航向角误差均方根Fig.16 RMSE of course angle with fusion algorithm and single model

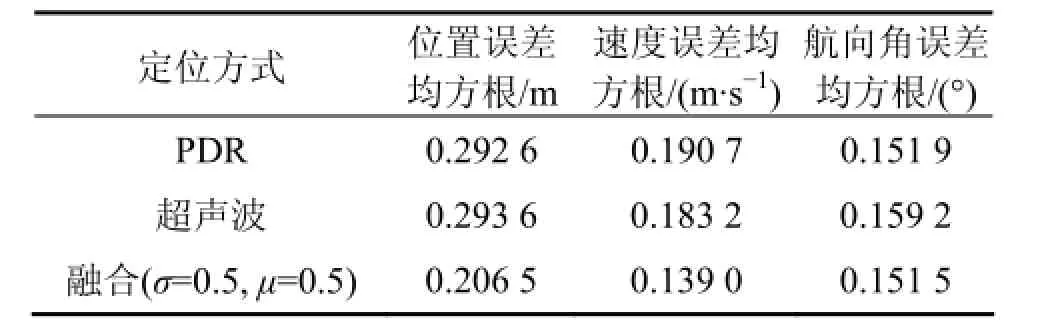
表7 有累积误差及有多路径环境下的误差均方根Table 7 RMSE with cumulative error and multipath effect

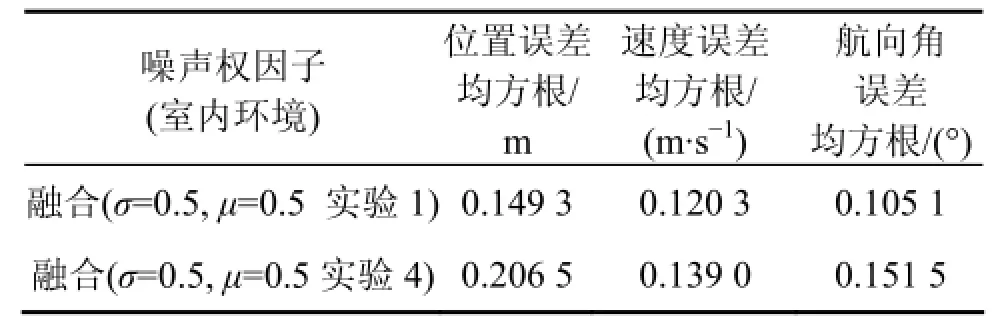
表8 实验1与实验4误差均方根对比Table 8 RMSE of experiment 1 and experiment 4

融合效果与实验1中误差均方根相比较，结果见表8。在PDR与超声波定位方案中各传感器测量精度一定的情况下，从仿真结果来看，PDR与超声波单模型方案定位误差均收敛在一定范围内，由于惯性器件累积误差与多路径效应造成 PDR与超声波定位误差较大，融合算法的定位性能仍然高于单模型，与PDR、超声波定位相比，位置（x， y）定位精度分别提高29.43%和29.67%；速度v精度分别提高27.11%和24.13%；航向角φ精度分别提高0.26%和4.84%。与实验1中室内环境相比，无论是单模型还是融合后的定位参数精度均有一定程度的下降。融合后，定位精度＜0.21 m，速度v精度＜0.14 m/s，航向角φ精度＜0.16°。

4 结论

1） 2组模型的融合定位与单模型相比，精度更高。

2） 室内环境复杂或系统运行较长时间时，与室内无遮挡无累积误差情况相比，融合定位精度略有下降但仍维持较高的精度，在一定程度上克服PDR的惯性器件误差随时间积累的缺陷与超声波定位由多路径效应产生的测距误差，提高系统在复杂环境下定位的适应性。

3） 融合定位参数误差均收敛在一定范围内，具有较强的稳定性与跟踪性能。

4） 引入反馈环节势必会增加融合中心的计算量，但反馈量仅仅是上一时刻的全局最优估计融合状态，不会给系统增加过多的开销，也不会影响系统的实时性。

［1］ 张凡， 陈典铖， 杨杰. 室内定位技术及系统比较研究［J］. 广东通信技术， 2012（11）： 2-5. ZHANG Fan， CHEN Diancheng， YANG Jie. Comparative study on indoor positioning technology and system［J］. Guangdong Communication Technology， 2012（11）： 2-5.

［2］ KUNDRA L， EKLER P. The summary of indoor navigation possibilities considering mobile environment［C］// European Regional Conference on the Engineering of Computer Based Systems. Budapest： IEEE， 2013： 165-166.

［3］ 赵锐， 钟榜， 朱祖礼， 等. 室内定位技术及应用综述［J］. 电子科技.2014， 27（3）： 154-157. ZHAO Rui， ZHONG Bang， ZHU Zuli， et al. Overview of indoor location techniques and application［J］. Electronic Sci， 2014，27（3）： 154-157.

［4］ 陈伟. 基于GPS和自包含传感器的行人室内外无缝定位算法研究［D］. 合肥： 中国科学技术大学信息科学技术学院， 2010：6-10. CHEN Wei. Research on GPS/self-contained sensors based seamless outdoor/indoor pedestrian positioning algorithm［D］. Hefei： University of Science and Technology of China. College of Information Science and Technology， 2010： 6-10.

［5］ 金宏斌， 戴林燕， 徐毓， 等. 基于无味卡尔曼滤波的多雷达方位配准算法［J］. 数据采集与处理， 2006， 21（1）： 29-33. JIN Hongbin， DAI Linyan， XU Yu， et al. Algorithm for multi-radar azimuth registration based on unscented Kalman filter［J］. Journal of Data Acquisition Proceeding， 2006， 21（1）：29-33.

［6］ SHEN Zhong， YU Wenbo， FANG Jiancheng. Nonlinear algorithm based on UKF for low cost SINS/GPS integrated navigation system［J］. System Engineering and Electronica， 2007，29（30）： 408-411.

［7］ 张志鑫， 张峰. 组合滤波器在组合导航中的应用设计［J］. 中国惯性技术学报， 2008， 16（2）： 188-191. ZHANG Zhixin， ZHANG Feng. Design of combined filter for integrated navigation system［J］. Journal of Chinese Inertial Technology， 2008， 16（2）： 188-191.

［8］ 司学慧， 李小兵， 张彦， 等. 基于平方根 UKF的多传感器融合再入段目标跟踪研究［J］. 系统工程与电子技术， 2012， 34（2）：303-306. SI Xuehui， LI Xiaobing， ZHANG Yan， et al. Multi-sensor fusion target tracking of reentry phase based on square-root unscented Kalman filte［J］. Systems Engineering and Electronics， 2012，34（2）： 303-306.

［9］ ASANO S， WAKUDA Y， KOSHIZUKA N， et al. Pedestrian dead-reckoning unit for navigation system using mobile device［C］// Global Conference on Consumer Electronics. Tokyo：IEEE， 2012： 530-534.

［10］ LAN K， SHIH W. Using smart-phones and floor plans for indoor location tracking［C］// IEEE Transactions on Human-Machine Systems. New Jersey： IEEE， 2014： 1-11.

［11］ FUJII M， OGAWARA R， HATANO H， et al. A study on position tracking system for pedestrian navigation using location and sensor information［C］// ITS Telecommunications （ITST）. Tampere：IEEE， 2013： 344-349.

［12］ FELIZ R， ZALAMA E， GARCIA-BERMEJO J G. Pedestrian tracking using inertial sensors［J］. Journal of Agents， 2009， 31（5）：35.

［13］ LEI Fang， ANTSAKLIS P J， MONTESTRUQUE L A. Design of a wireless assisted pedestrian dead reckoning system-the Nav Mote experience［J］. Instrumentation and Measurement， 2005，54（6）： 2342-2358.

［14］ 原新， 王东阳， 严勇杰. 基于推算定位的超声波定位融合的机器人自主定位技术［J］. 海军工程大学学报， 2009， 21（5）：67-72. YUAN Xin， WANG Dongyang， YAN Yongjie. Self-positioning of robot based on dead reckoning and ultrasonic data fusion［J］.Journal of Naval University of Engineering， 2009， 21（5）： 67-72.

［15］ 成兰， 谢恺. 迭代平方根 UKF［J］. 信息与控制， 2008， 37（4）：439-444. CHENG Lan， XIE Kai. Iterated square root unscented Kalman filter［J］. Information and Control， 2008， 37（4）： 439-444.

［16］ 刘铮. UKF算法及其改进算法的研究［D］. 长沙： 中南大学信息科学与工程学院， 2009： 16-19. LIU Zheng. Research of UKF algorithm and improved algorithm［D］. Changsha： Central South University. School of Information Science Engineering， 2009： 16-19.

［17］ MERVE R V D， WAN E. The square-root unscented Kalman filter for state and parameter-estimation［C］// Acoustics， Speech，and Signal Processing. Salt Lake City， UT： IEEE， 2001：3461-3464.

［18］ 张伟， 王泽阳， 张珂. 基于多模型航迹质量的融合算法［J］. 计算机科学， 2013， 40（2）： 65-69. ZHANG We， WANG Zeyang， ZHANG Ke. Track-to-track fusion algorithm based on track quality with mutiple model［J］. Computer Science， 2013， 40（2）： 65-69.

［19］ ZHANG Yu， RAN Jinhe. Dynamic weighted track fusion algorithm based on track comparability degree［C］// Information Theory and Information Security （ICITIS）. Beijing： IEEE， 2010：710-713.

［20］ 崔波. 多传感器目标跟踪数据融合关键技术研究［D］. 成都：西南交通大学信息科学与技术学院， 2012： 48-57. CUI Bo. Key technologies research on multi-sensor data fusion for target tracking［D］. Chengdu： Southwest Jiaotong University. School of Information Science and Technology， 2012： 48-57.

［21］ 田雪怡， 李一兵， 李志刚. 航迹融合算法在多传感器融合中的应用［J］. 计算仿真， 2012， 29（1）： 53-56. TIAN Xueyi， LI Yibing， LI Zhigang. Application of the track fusion in multi-sensor fusion［J］. Computer Simulation. 2012，29（1）： 53-56.

［22］ HAYWARD R， MARCHICK A， POWELL J D. Single baseline GPS based attitude heading reference system （AHRS） for aircraft applications［C］// Proceedings of the American Control Conference 5. San Diego， CA： IEEE， 1999： 3655-3659.

（编辑 陈爱华）

Fusion algorithm in indoor integrated position system for pedestrian dead reckoning/ultrasonic

ZHAO Yanpeng， SHI Wei， AI Mingxi

（School of Aeronautics and Astronautics， Central South University， Changsha 410083， China）

To improve the precision and tracking performance of indoor position system and adapt to the complex indoor environment， the position systems of pedestrian dead reckoning and ultrasonic transducer were integrated. What’s more，the fusion algorithm of noise power factors assisting covariance weighted fusion based on Square Root Unscented Kalman Filter was proposed， and the globally optimal state estimation as feedback was introduced into the algorithm too. To solve the problem of measuring pedestrian’s course angle with ultrasonic， a simple and effective geometry method was proposed. The simulation result shows that in the simulative and dynamic indoor environment including the influence of multipath effect and cumulative error of inertia device， the position accuracy of fusion algorithm is always better than that of single position model’s. Moreover the fusion algorithm has good convergence performance， stability and adaptation performance. So the study has positive effect on indoor position research and application.

indoor position； Square Root Unscented Kalman Filter； noise power factors； covariance weighted fusion；course angle measurement

V249.3

A

1672-7207（2016）05-1588-11

10.11817/j.issn.1672-7207.2016.05.019

2015-06-04；

2015-08-28

国家自然科学基金资助项目（61174002） （Project（61174002） supported by the National Natural Science Foundation of China）

时伟，博士，副教授，从事室内导航与定位、飞行器导航与控制技术研究；E-mail： ahshw@csu.edu.cn