例谈计数器在三年级口算乘、除法中的运用
李晓华 夏瑞雪
【摘 要】计数器的使用范围大多是在教学认识数的时候,借助计数器来体会十进制计数单位,包括数的组成、读数和写数。其实在三年级口算乘、除法时也可以使用计数器,帮助学生理解算理、掌握算法,从而完成从生活世界到数学世界的数学化过程。
【关键词】计数器 抽象概括 口算乘除法
计数器是小学数学教学中常见的教学工具,从认识十以内的数开始,一直到大数的认识,都离不开计数器,教材中将生活中的具体数量引入,然后半抽象到计数器上,最后再抽象成数字,计数器在这个过程中起到了中转的作用。因为计数器有别于生活中的具体数量,既略为抽象,又具有一定的操作性。小学生思维能力的发展是沿着操作水平到表象水平再到分析水平逐步提高的,对应的智力发展阶段是从动作认知到图形认知再到符号认知。因此,计数器是学生从生活世界走向数学世界的桥梁。然而在课堂教学中,计数器的使用还有待于挖掘和提高,目前,计数器的使用范围大多是在教学认识数这一内容时使用,借助计数器来体会十进制计数单位,包括数的组成、读数和写数。有的教师在教学进位加法和退位减法时也会用到计数器。但是很少有教师在三年级上册的口算一个数是整十、整百、整千数……的乘法时使用计数器,更少有教师在三年级下册的口算被除数是整十、整百、整千数……的除法时使用计数器。笔者通过自身的教学实践,来谈如何在三年级口算乘除法时使用计数器,帮助学生理解算理、掌握算法,完成从生活世界到数学世界的数学化过程。
一、计数器在三年级上册口算乘法中的运用
(一)生活引入
人教版三年级上册第56页主题图:坐碰碰车每人20元,3人需要多少钱?
学生根据题意列出算式:20×3。很多学生都知道答案等于60,这时教师提问:你是怎么想的?引出学生的各种想法。
从生活中引入学习内容,唤起学生的已有经验,尤其是大部分学生都知道20×3的积是60,部分学生能表达出自己的思考过程:因为2×3=6,所以20×3=60,在算法上确实如此计算,但是隐藏在这个背后的算理是什么?我们可以借助计数器来帮助学生理解算理。
(二)半抽象:计数器
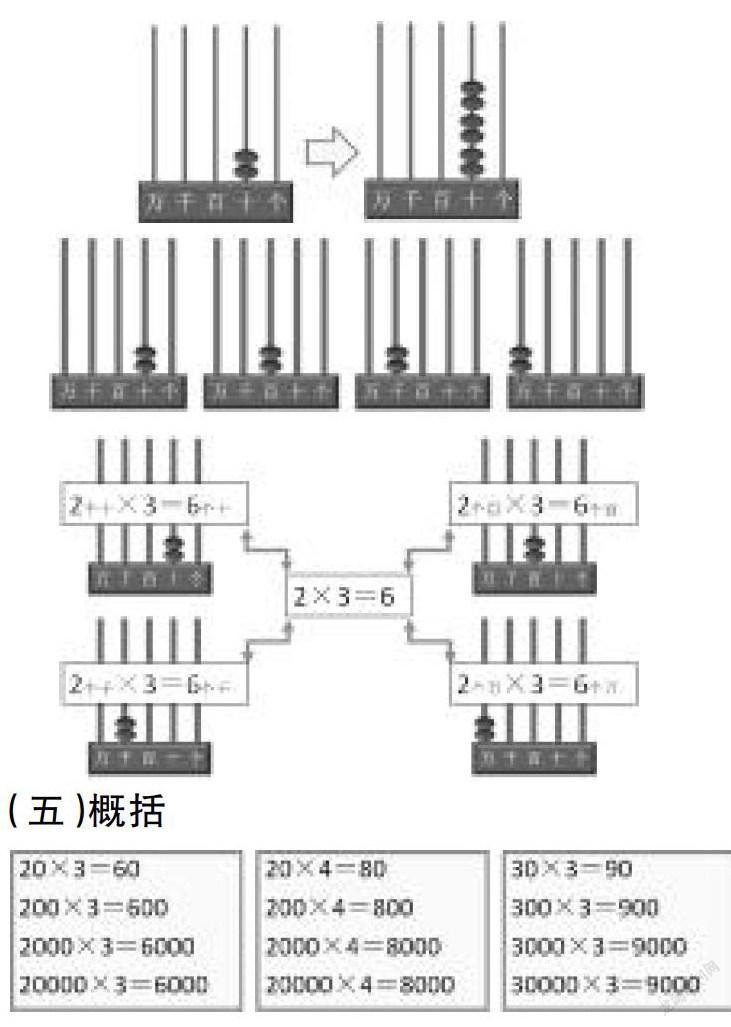
大部分学生都是因为2×3=6,所以20×3=60。提出疑问:2×3=6与20×3=60之间有什么联系呢?借助计数器演示:20在计数器上是表示2个十,2个十乘3是6个十,就是60。
在算式上看到的是20×3,而在计数器上看到的是2×3,因为计数器上有数位,学生很清楚地理解了20表示2个十,2个十乘3是6个十,就是60。计数器将2×3=6和20×3=60串联起来,沟通了算法和算理,不仅知其然,更是知其所以然。
(三)迁移:从整十数迁移到整百、整千、整万数……
计数器上的这些珠子可以用哪道乘法算式来表示呢?出示下图,列式并说算理:200在计数器是表示2个百,2个百乘3是6个百,等等。从20迁移到200、2000、20000,数字变了,算理也随着计数器上珠子的位置变化而变化,从几个十到几个百,再到几个千乘3。
(四)抽象
观察这四个计数器及乘法算式,你发现了什么?引导学生发现算式不同,但是在计数器上珠子的数量是一样,都是2颗珠子,都是可以用2×3=6来思考。如下图。
(五)概括
如果把2×3=6换成2×4=8,那么可以写成哪些一个数是整十、整百、整千数的乘法?
如果换成是3×3=9呢?
观察这三组算式,一个因数是整十、整百、整千数,一个因数是一位数,在计算方法上有什么相同的地方?全都可以转化成表内乘法。为什么可以这么算?因为可以把整十、整百、整千数看成是几个十、几个百或者几个千乘一位数。
至此,从生活中的数学计算,到计数器上的计算,再到纯符号的运算,学生不仅掌握了计算方法,更明白了算理,从操作水平开始,通过计数器这一载体,发展到符号水平,完成了数学化的过程。
二、计数器在三年级下册口算除法中的运用
(一)生活引入
人教版三年级下册第11页例1:把60张彩色手工纸平均分给3人,每人得到多少张?
学生根据题意列出算式是60÷3,问学生是怎么计算的,很多学生都说是因为6÷3=2,所以60÷3=20,再追问为什么可以这么计算呢?就回答不了了。其实这是引导学生发现算法背后的算理。没有算理的支撑,算法是单薄的,必须让学生明白6÷3=2和60÷3=20之间的关系。
(二)半抽象:计数器
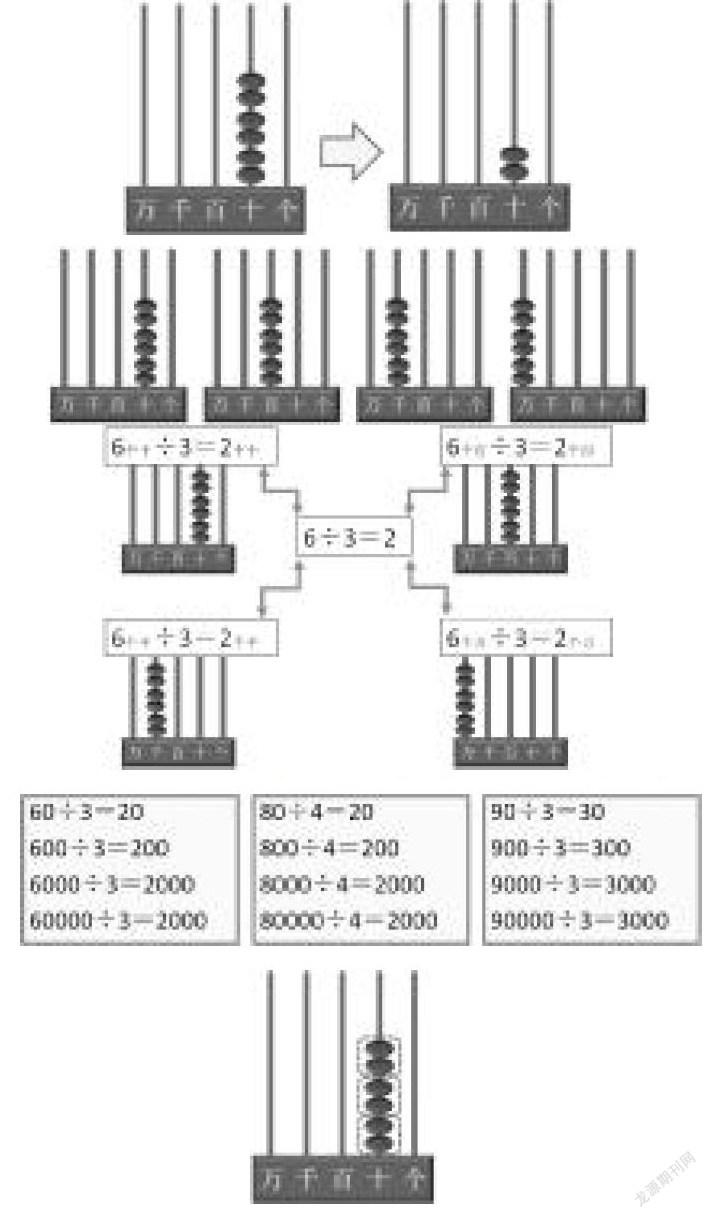
将60÷3=20在计数器上表示出来是怎样的呢?请看下图,计数器将60转化成了6个十,学生发现60÷3=20就是6个十除以3等于2个十,就是20。在计算的过程中深刻领会了算理,再去计算其他题目时,就会调用头脑中计数器这个表象,快速地实现从生活数学到符号数学的转化。
(三)迁移:移动珠子在计数器上的位置
如果将计数器上的珠子从十位移动到百位,你得到的是哪道除法算式?如果移动到千位呢?万位呢?学生根据计数器上珠子在不同的位置列出不同的除法算式。
(四)抽象
根据计数器上的珠子,分别写出下列算式,再进行抽象:这些算式在计算方法上有什么相同点?都是可以转换成6÷3=2来计算。
(五)概括
变换数字,又可以写成哪些算式?然后观察这些算式,进行思考:这些算式有什么相同的地方和不同的地方?被除数是整十、整百、整千的,除以一位数,为什么可以化成表内除法来计算?挖掘计算方法背后的算理,那就是把整十、整百、整千数看成几个十、几个百、几个千来计算。算式从特殊到一般,再从一般到特殊,深刻理解了算理,掌握了算法。
三、利用计数器沟通口算乘除法之间的联系
乘法和除法之间存在天然的亲密关系,而口算乘法和口算除法无论在外在表现形式上还是内在算理上,也有着千丝万缕的联系。在教学三年级下册的口算除法时,可以引导学生回忆三年级上册的口算乘法,再结合口算除法的算理,两者的相同点都是把整十、整百、整千数看成几个十、几个百、几个千来计算。
比如根据上图写一道乘法算式和一道除法算式,学生看到的都是6颗珠子,而表现出来的算式却是20×3=60和60÷3=20,如果追问它们之间的关系,那就是都转化成几个十来计算。一个是表内乘法,一个是表内除法,然后再深挖,那就是全部都出自同一句乘法口诀:二三得六!最终,让三年级的口算乘法和口算除法回归到二年级的表内乘法口诀,实现了由薄到厚,再由厚到薄的知识发展过程,竖成线、横成片。
数学学习的过程是一个螺旋上升的过程,学生在二年级熟练掌握的乘法口诀,在三年级的口算乘法和口算除法中得到了应用,通过计数器这一载体,沟通了三者之间的联系,随着年级的升高,学生的智力发展水平也从动手操作水平发展到了图形表象水平,进而进入符号运算水平,在二年级时需要摆弄小棒的,到了三年级时就用看计数器的图片就能明白算理了,到四年级几乎就可以脱离图形,独立地进行符号运算了。这是一个智力水平发展的过程,也是知识能力不断提升的过程,在这个过程中,我们不应该忽视中间环节——图形表象的作用,计数器在三年级口算乘除法中得到的充分应用,正符合了学生的思维发展水平。
(浙江省瑞安市马鞍山实验小学 325200)

