基于符号动力学的变压器内部故障检测
李 涛 高 晓 陈巍家
(湖南大学信息科学与工程学院,长沙 410082)
基于符号动力学的变压器内部故障检测
李 涛 高 晓 陈巍家
(湖南大学信息科学与工程学院,长沙 410082)
针对变压器状态检修,本文提出了基于符号动力学对变压器内部故障进行在线检测的方法。此方法无需外部传感器,可以快速有效发现变压器潜在内部故障以及严重程度。首先建立起变压器内部故障非线性数学模型并仿真出不同程度的匝间短路故障,获取源边非线性电流信号并符号序列化,对符号化后的序列构建马尔科夫概率转移矩阵并建立起信号异常度测量机制。仿真结果表明随着匝间短路故障程度的加深,符号动力学方法能够有效诊断出对故障电流信号与正常信号之间的差异,此为变压器状态检修提供了坚实的依据。在此基础上,本文结合现场故障数据进行了验证分析,进一步证实了符号动力学在检测变压器内部故障上的有效性。
符号动力学;变压器内部故障;最大熵划分;马尔科夫状态矩阵
变压器作为电网传输电能的主要枢纽,是电力系统中最重要的电气设备之一。本文着重分析电力变压器的内部故障,及时发现变压器内部故障对于电力系统安全可靠运行有着重大意义。
目前对变压器内部故障在线检测的方法主要还是通过复杂的外部传感器,如:利用红外线设备监测变压器的内部温度;直接在变压器内部安装摄像头进行视频监控;利用漏电感法将探测线圈探测变压器内部漏磁通变化等[1-2]。根据变压器设备运行参数来进行检测的有:电压电流比法、油中气体分析法以及功率损耗法等[3-4]。油中气体分析法和电压电流比法并不能诊断故障的程度,而功率损耗法基于损耗功率诊断故障程度,不能准确估测匝间短路发生的具体时刻。近年来,国内外学者对变压器内部故障体系进行了深入研究,引入神经网络、专家理论、灰色理论和模糊理论等多种诊断方法,尝试建立起综合在线评估系统[5-6]。而本文提出一种新的基于符号动力学的变压器内部故障检测方法,可作为该系统的重要参考指标之一。
本文旨在对变压器内部故障进行在线检测,同时对运行中的变压器状态进行有效评估。文章首先给出变压器数学方程来建立其内部故障的非线性的工作理论环境,论证了其非线性系统的本质,说明其可以用符号动力学进行检测和分析。通过仿真获取不同程度的变压器匝间短路故障,运用符号动力学方法将抽象的故障信号符号序列化,并构建相应的马尔科夫概率转移矩阵,根据矩阵向量的欧式距离建立起信号异常度机制,实现对变压器运行状态进行实时监测。此方法能够快速准确诊断出其内部潜伏性故障以及内部故障的严重程度,无需额外的传感器设备。为了较好地证明符号动力学对故障信号检测的有效性,本文利用符号动力学方法对变压器仿真内部故障以及现场故障数据分别作了有效验证,开辟了变压器在线检测的一个研究方向。
1 变压器内部故障非线性本质分析
1.1变压器内部故障
由于变压器的结构非常复杂,故障类型比较多,很难有一个对变压器故障进行划分的标准。本文在基于其他学者对变压器故障划分方法的基础之上,以主体结构划分为主导,结合变压器的故障易发区,将变压器的故障划分为以下几大模块,如图1所示。
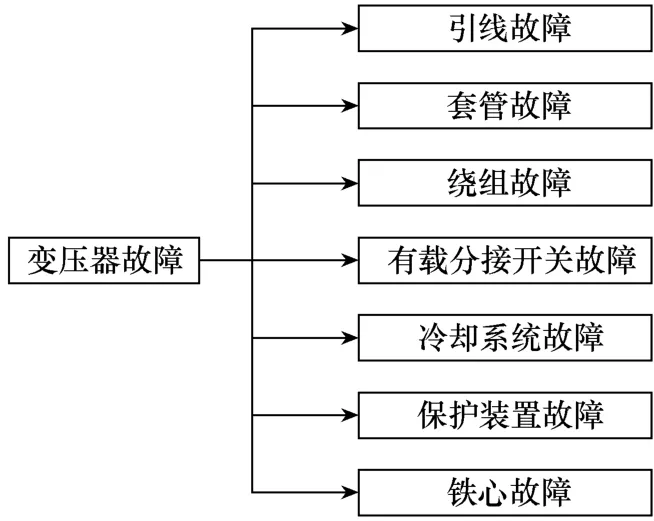
图1 变压器故障分类
变压器内部故障主要发生在其内部绕组上,而常见的内部电气故障主要有:匝间短路、匝地短路、相间短路以及铁心故障。其中匝间短路在变压器内部故障中较为常见,因此本文以匝间短路故障为实验仿真对象,利用符号动力学的方法对其建立起信号差异机制从而诊断变压器内部故障。
1.2变压器的数学模型
本文在分析单相双绕组变压器数学模型的基础上,介绍一种以磁链作为状态变量联系电流和电压的变压的数学模型[7],与以电流作为状态变量的模型相比,此模型物理概念清晰、仿真效率高。
1)磁链方程
考虑变压器绕组漏磁通,则一、二次磁通可以用下式表示:

式中,φm代表主磁通,φl1和φl2代表—、二次绕组的漏磁通。
绕组1的匝数为N1,一次绕组磁链表示为
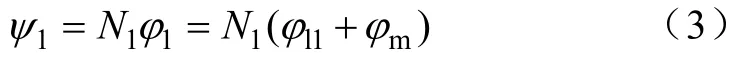
磁通等于磁动势乘磁阻,式(3)改写为
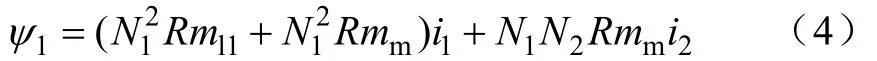
式中,绕组 1的磁动势为N1i1,其漏磁通磁路的磁阻为Rml1,主磁通磁路磁阻为Rmm。
同理,对于绕组2的磁链有
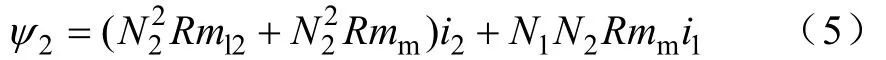
则—、二次绕组关于绕组感应可以表达为

式中,L11、L22分别为—、二次绕组的自感;L12为—、二次绕组互感。 L11表示—次绕组的漏电感和电流i1单独在—次绕组上起作用的电感的和。则有
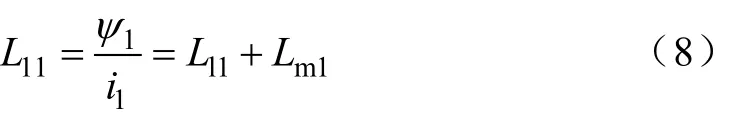
同理:
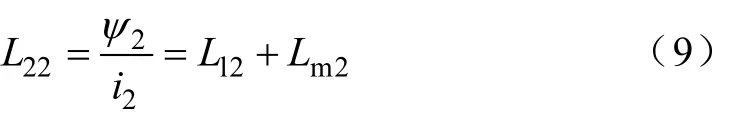
根据匝比有

2)电压方程
一次绕组感应电压可以由式(4)表达为
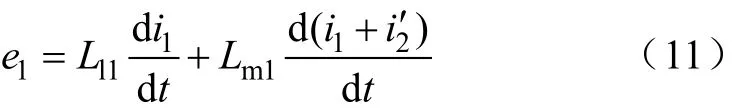
同理:

绕组端电压为感应电压与阻抗压降之和,则绕组端电压的电压表示为

1.3内部故障仿真模型
将—、二次绕组磁链作为状态变量,所以绕组端电压可以用式(13)、式(14)表示为
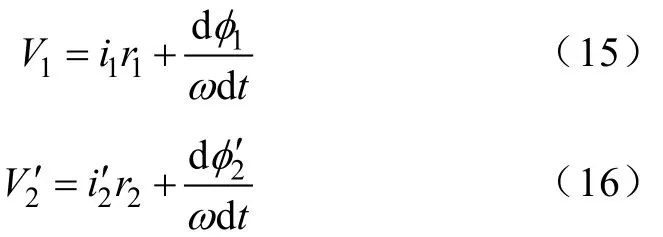
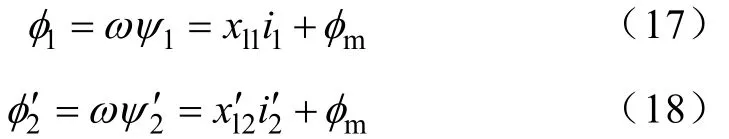
其中

由式(17)、式(18)利用磁链表示绕组电流为
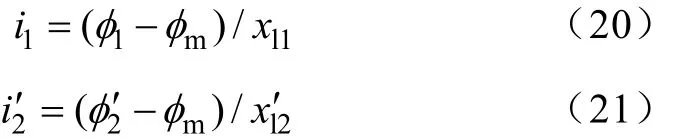
将电流公式代进式(19)得
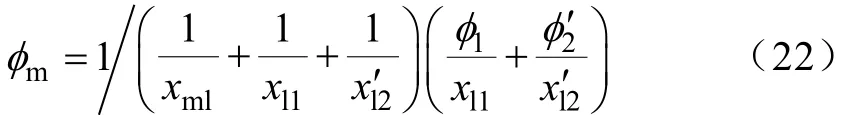
将电流式(20)、式(21)代进电压式(15)、式(16)中,得到状态磁链的积分关系公式为
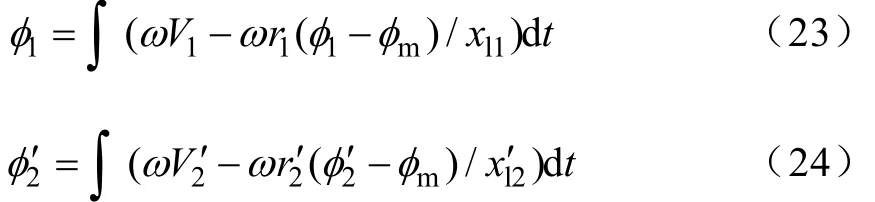
式(20)至式(24)就构成了由电压、磁链、电流描述的变压器工作的基本非线性动态模型。其中,若考虑铁心饱和的情况,可以在式(22)中加表示饱和磁通和当前磁通的差值,这样保证主磁通不会无限地增大,进而模拟出铁心饱和的情况。
变压器的匝间短路故障仿真实际上等效于变压器某一绕组上的匝数减少或者阻抗下降,由于本文只需匝间短路故障数据建立起差异机制,因为仿真忽略外部环境因素。本文将两个绕组代替故障绕组,总阻抗与原绕组阻抗等值,即:因此,只需要修改二者的数值即可模拟出不同严重程度的变压器匝间短路故障。
2 基于符号动力学的信号处理
符号动力学起源于非线性动力系统,为非线性研究提供了一种新型的状态分析方法。近些年其发展研究领域已不再局限于动力系统。研究数据表明,其在金融、物理气象、生物医学等方面都有着较好的应用[8-10]。
符号动力学用有限的状态空间来描述系统状态的思想也被运用到对信号的描述上。这是一个“粗粒化”过程。这一过程能够捕获系统大尺度的特征。作为一种对动力系统粗粒化的描述,它保留了原信号的拓扑结构,并且有效地进行了信噪分离,能够更加快速地发现系统的特征[11]。
首先,适当的相空间划分是符号动力学中的关键步骤。相空间划分的目的是为了得到一个保留原信号特征最佳的符号序列[12],符号动力学算法的快速性、较强的辨识与分类功能,使其适合于提取非线性动力学数据序列大尺度的特征。每一个划分表示系统处于某个状态,相应的符号序列代表系统此时的状态。常用的方法有基于方差的划分、最大熵划分、分层划分等都有其各自的特点[13]。本文采取最大熵划分方法,使符号序列尽可能保留原信号的最大信息量,在很大程度上表征了信号中的特定成分,不仅考虑了全局特征也提取了局部细节信号[14]。
对于非线性的变压器内部故障信号,正常和故障的电流信号符号化后的序列代表着变压器系统的两种不同状态,且两种状态的迁移过程能够被符号动力学所发现,其故障严重程度可以认为是计算相空间中两个信号轨道之间的偏离程度。通过计算就可以发现并预测变压器内部的早期故障。
2.1最大熵划分重构相空间
系统的某一时刻状态称为相,而决定状态的几何空间称为相空间。一般来说,非线性系统相空间维数可能很高,甚至是无穷。在实际工程应用中,一般的数据采集设备只能得到反映该系统特征的一维向量,即符号序列。因此,如何对信号进行相空间重构并提取相应系统特征信息是本文的首要任务。这里本文利用信息熵理论对相空间重构进行定性分析,信息熵是通过一种数学的方式度量信息中所包含的信息量[15]。对于符号动力系统,信息熵的表达式为
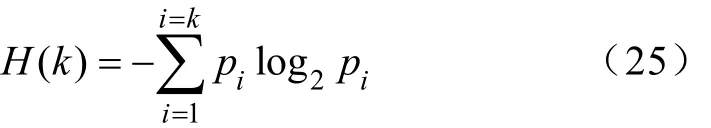
式中,ip代表符号序列第 i个字符出现的频率。根据上式可知每个字符频率出现一致时,H(k)拥有最大值。
通过理性分析,在相空间重构中,信号变化愈是激烈的区域应该予以更多的符号字母表达,这样划分得到的序列才会保留原信号的最大信息量[16]。具体的基于最大熵划分算法流程如图2所示。
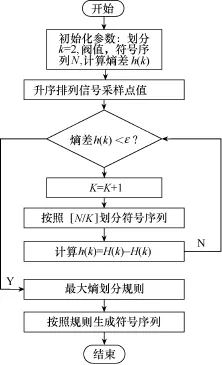
图2 最大熵划分算法流程
在最大熵划分中,一般来说,字母表越大,划分效果越好,但这丧失了符号动力学的基本优势:简洁性以及快速性。最终划分数目 k,即划分的精度跟最大熵中的门限阀值ε有关,具体见3.1节。
2.2马尔科夫状态转移概率矩阵
由于符号序列每个位置出现的符号取值是离散的,并且不同符号出现的概率取决于整个信号符号化之后的结果。因此,此时信号本身就可以作为一个离散时间离散值的随机过程来进行描述和分析。在这个随机过程中,存在一个或多个符号出现多次的现象,这表示系统处于某一特定的状态。这个随机过程就是系统在这些状态之间以特定的概率跳转的过程。而一些固定出现的状态以及它们对应的转移概率构成的几何结构就是该随机过程中存在的模式,这是一个马尔科夫过程。具体来说,对于一个符号序列tS,符号字母表大小为 k,滑动窗口长为D,从逐个符号序列第一个符号字母开始,以每窗口长为D向右平移,每滑过一个符号字母,依次保留前一个状态的后(D-1)个符号字母并添加一个新的符号字母产生一个新的状态。 马尔科夫模型基于以下理论:
1)对于一个符号序列,下一个出现的符号与之前D个时刻符号相关,则称这个过程为D阶马尔科夫过程,即
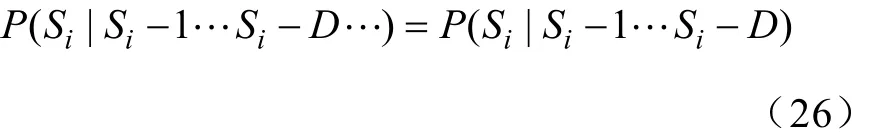
设置字母表为 A,其大小为|A|,则此序列得到的马尔科夫过程所有可能出现的状态数量应该为对系统观察过程中可能出现的符号序列集合若两个原符号序列包含同长度D的短序列则该集合中满足该条件称为等价状态,表达式为
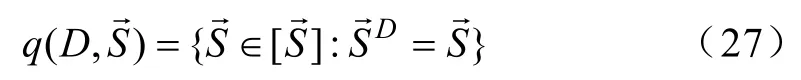
所有等价状态集合为
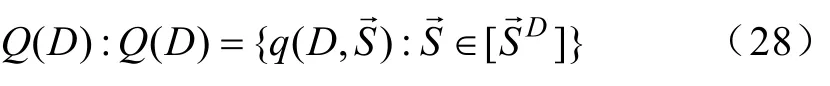
2)定义ip和jp分别为系统中的等价状态,状态集Q中的第i个状态转移到第j个状态的概率为
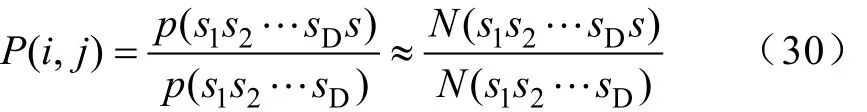
那么,由这个序列得到所有的状态之间转移概率可以用一个矩阵描述,即马尔科夫矩阵[17]。
简单来说,若符号的字母表A只包含两个字母{0,1},马尔科夫过程中下一个状态只和之前的二个符号有关,那么最简单的马尔科夫过程可以表示为
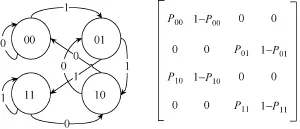
图3 马尔科夫矩阵
且马尔科夫矩阵应该有

2.3信号异常度
在获取相应的马尔科夫状态概率转移矩阵之后,即可用该矩阵描述当前系统的拓扑结构以及状态转移等系统特征。
将正常电流信号所对应的标准符号序列建立的马尔科夫状态转移概率矩阵记为π0,故障电流信号所对应的马尔科夫状态转移概率矩阵记为πi,则整个系统的行为变化可用如下异常度表示:
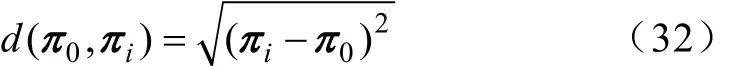
式中,对于参数 d,本文采取的是较为普遍的欧式距离。因此,衡量故障信号与正常信号之间的差异程度只需简单的运算两个转移概率矩阵之间的欧式距离,便可以诊断变压器当前的运行状态。
3 实验及结果分析
为了验证符号动力学诊断故障信号的有效性,本文在仿真故障数据和现场故障数据上分别做了相关实验。首先,我们对最大熵划分算法符号集大小以及马尔科夫状态阶数进行了选取测试。
3.1符号集参数选取
对于信号的相空间划分,本文先采用标准正弦信号进行初步测试,正弦信号是信号处理过程中一种比较常用的信号样式,根据傅里叶变换关系,所有信号都可以看成是多种正弦信号的一种组合,因而研究正弦信号是进行信号特征分析的基本前提。根据 2.1节最大熵算法对信号进行划分,分析得到信号的熵差随符号划分数k的变化如图4所示。
算法中较小阈值ε可以让符号集很大,从而使信号的划分更为精确,但同时需要更大的计算量,导致算法时间过长。

图4 熵差随划分数变化图
为了更好地验证符号集大小对信号的区分效果,本文选取正弦信号幅度的1倍变化到3倍来对符号集A进行有效测试。
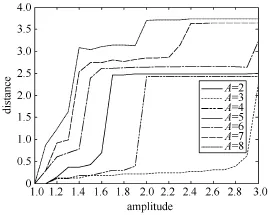
图5 符号集大小对区分影响
由图5知,除了符号集为2其他所有曲线趋势都为增大,初步验证马尔科夫机算法的有效性。符号集的增大导致曲线陡峭点提前到来,在变化区间以及区分度效果上选取4~6较为合适。
因此,本文根据图 4、图 5以及实际经验综合考虑算法的准确度和系统的实时性等因素,选取划分的符号集大小为6,最大熵算法阈值ε=0.2。
3.2马尔科夫机状态阶数D
状态阶数D是马尔科夫状态机中独有的参数,D的变化意味着马尔科夫过程中下一个状态和过去更多的状态相关。对此,选取正弦信号从幅度和相位两个方面对从参数D进行有效测试。
增加D的大小,可以从宏观的角度观察同一个系统状态下两个信号的变化趋势,从图6可以看到:随着D取值变化,信号差异的整体趋势变大,马尔科夫法对信号故障状态的区分能力越强。
为探究其随信号相位的影响,将测试信号相位从 0°变化到 90°进行比较生成实验效果图如图 7所示。
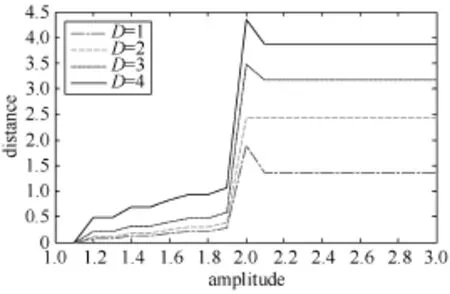
图6 状态阶数D随信号幅度大小效果图
图7是信号轨道间的矩阵欧式距离与相位变化的关系图,相位的波动并未明显改变系统状态的变化规律,但随着D的增大,根据状态数为|A|D知算法的计算量将成指数增加从而导致算法执行时间过长。在幅度效果图6中,只有D取2时没有产生瑕疵尖波,因此,综合考虑选取区分度较好的D=2。
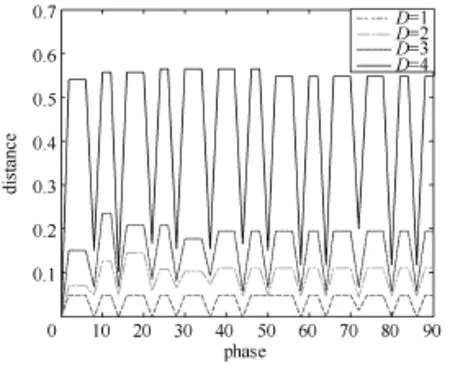
图7 状态阶数D随信号相位效果图
综上所述,马尔科夫机状态法能够有效针对信号差异进行识别,将采取符号集大小为 6,状态阶数D=2测试仿真故障数据。
3.3仿真故障数据实验
结合第 1节介绍的变压器数学模型,本文在Matlab/Simulink环境下模拟对变压器匝间故障的仿真,仿真变压器的参数见表1。
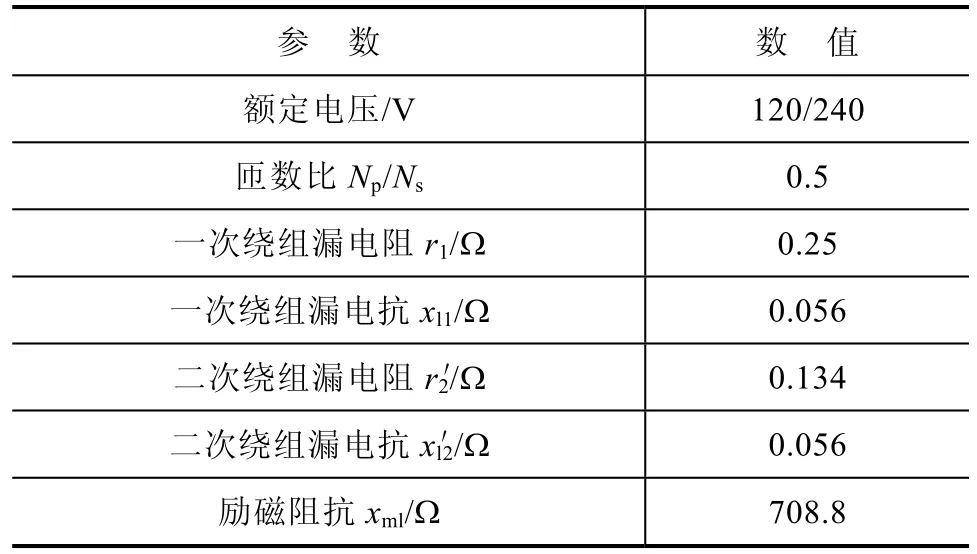
表1 仿真变压器参数
利用仿真模型得到的数据,在负载一定的情况下,本文将绕组阻抗依次减少至30%,模拟仿真了变压器内部匝间短路故障的8种情况,并运用符号动力学方法对故障信号数据与标准正常信号进行对比,得到表2中的结果。
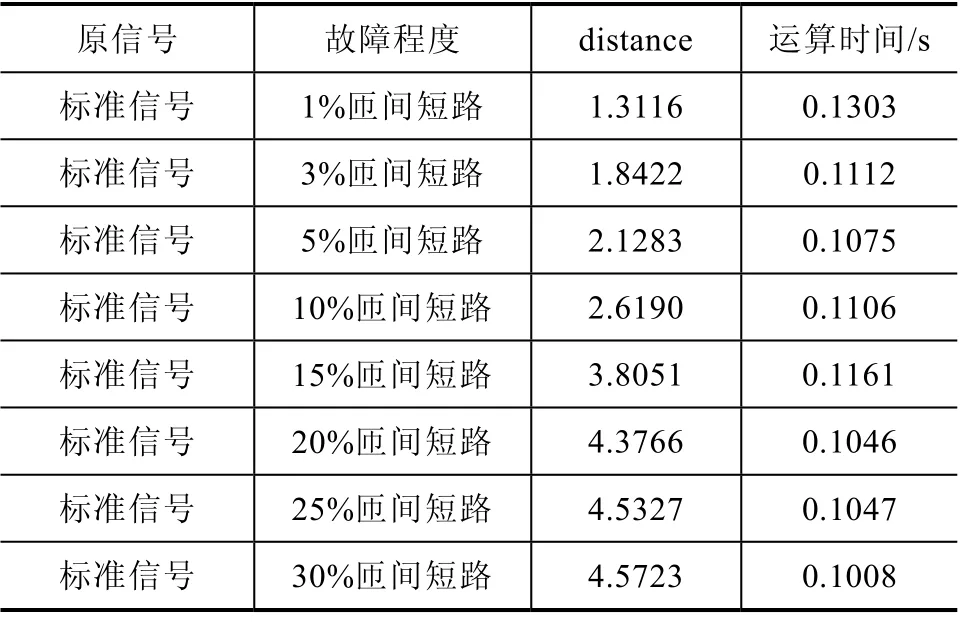
表2 变压器匝间故障测试
由表2可知,随着故障程度加深,马尔科夫转移概率矩阵之间的距离明显增大,运用符号动力学方法可以快速有效地检测出信号差异。
图8直观地展现了匝间短路故障测试结果。符号动力学算法的运算执行平均时间约为0.11s,因此可以实时在线对信号进行有效检测,以此来诊断变压器的运行状态。

图8 变压器匝间故障测试
需要补充的是,虽然本文仅针对变压器的内部匝间故障进行了仿真,并运用了符号动力学予以验证。但变压器的其余3种内部故障的本质特性都是系统内部绝缘的问题,而在变压器的内部,电能一直通过磁场来进行传递,电路以磁链作为状态变量联系电流和电压的变压器数学微分方程固定不变,即
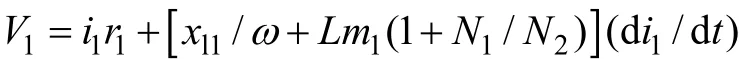
3.4现场故障数据实验
本文从供电局获取了变电站多种变压器区内故障的原边电流信号的录波数据,如图9所示。

图9 变压器现场故障数据
对于电流信号 a、b、c三相分别采用符号动力学方法进行分析,得到相关结果见表3。

表3 变压器现场数据测试
因为本文获取的故障数据早已表明变压器发生了比较严重的内部故障,所以对于表3中通过符号动力学运算得到的欧式矩阵距离数值比较大,这表明实验结果与所获取的现实情况相符合。通过现场故障测试表明,符号动力学算法能够诊断出故障信号程度,运算时间短,因此我们可以相信该诊断方法可靠、有效。
4 结论
本文提出了一种基于符号动力学的变压器内部故障在线检测的新型方法。在相空间的划分中,采用最大熵算法对原始信号进行粗粒化和序列化,最大限度地保留信号的细节信息。为了获取动态系统的定性信息以及状态演化,本文通过建立马尔科夫转移概率矩阵方法对符号化后的信号特征进行有效提取,在信号异常度分析时使用欧式矩阵距离作为故障程度标志,并通过 distance数值为变压器标注了健康、亚健康、故障三种状态。实验结果分析表明,针对在线运行的变压器电流信号数据,符号动力学方法可以快速诊断出变压器早期内部故障并能够对当前的运行状态进行有效地评估,无需外部传感器设备。此为其状态检修系统提供了一种更为经济简单的检测方法。此外,结合该算法本身的鲁棒性,该方法也同样适用于其他家用电器以及工厂大型电气设备等,对于风险防范和故障监控具有重要意义。
[1] Prosr P, Brandt M, Mentlík V, et al. Condition assessment of oil transformer insulating system[C]// International Conference on Renewable Energies and Power Quality: Granada, 2010: 23-25.
[2] 郝治国, 张保会, 李朋, 等. 漏电感参数辨识技术在线监测变压器绕组变形[J]. 高电压技术, 2006,32(11): 67-70, 73.
[3] 廖瑞金, 杨丽君, 郑含博, 等. 电力变压器油纸绝缘热老化研究综述[J]. 电工技术学报, 2012, 27(5):1-12.
[4] 谭喜堂, 吕佩佩, 朱琴跃, 等. 单相双绕组变压器匝间短路故障诊断[J]. 电气自动化, 2015, 10(1): 73-74,107.
[5] 张镱议, 廖瑞金, 杨丽君, 等. 基于云理论的电力变压器绝缘状态评估方法[J]. 电工技术学报, 2012,27(5): 13-20.
[6] 蔡红梅, 陈剑勇, 苏浩益. 基于灰云模型的电力变压器故障诊断[J]. 电力系统保护与控制, 2012,40(12): 151-155.
[7] 李晓庆, 陈尔奎, 纪志成. 基于 MATLAB单相变压器的仿真建模及特性分析[J]. 变压器, 2005, 42(3):8-12.
[8] Varga D, Loncar-Turukalo T, Bajic D, et al. Symbolic dynamic analysis of heart rate and blood pressure time series of rats[C]//2007 5TH INTERNATIONAL SYMPOSIUM ON INTELLIGENT SYSTEMS& INFORMATICS, 2007: 171-174.
[9] Halizi CR, Crutchfield JP. Computational mechanics:patternand prediction, structure and simplicity[J]. Journal of Statistical Physics, 2001, 104(3/4): 817-879.
[10] Kaddoum G, Gagnon F. Performance analysis of communication system based on chaotic symbolic dynamics[C]//Signals and Electronic Systems (TCSSES),2010 International Conference on IEEE, 2010: 307-310.
[11] 宋爱玲, 黄晓林, 司峻峰, 等. 符号动力学在心率变异性分析中的参数选择[J]. 物理学报, 2011, 60(2):126-133.
[12] Shalizi CR, Crutchfield JP. Computational mechanics:pattern and prediction, structure and simplicity[J]. Journal of Statistical Physics, 2001, 104(3/4): 817-879.
[13] Veen MJ. Reinders M J T,bolt E M,et al. A Ma ximumvariance clusteral gorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2002, 24(9): 1273-1280.
[14] Rajagopalan V, Ray A. Symbolic time series analysis vi awavelet based partitioning[J]. Signal Processing,86(11): 3309-3320.
[15] 王松岭, 许小刚, 刘锦廉, 等. 基于符号动力学信息熵与改进神经网络的风机故障诊断研究[J]. 华北电力大学学报(自然科学版), 2013, 40(4): 51-58.
[16] Rajagopalan V. Asok ray[J]. Symbolic time series analysis via wavelet-based partitioning.Signal Processing 86(2006): 3309-3320.
[17] Minku LL, Yao XD. A new ensemble approach fordealing with concept drift[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(4): 619-633.
[18] 周迅, 向馗, 俞小莉. D-Markov模型在疲劳裂纹扩展模式识别中的应用[J]. 浙江大学学报(工学版),2008, 42(3): 549-552.
[19] Ray A. Symbolic dynamic analysis of complex systems for anomaly detection[J]. Signal Processing, 2004,84(7): 1115-1130.
电力数据的处理方法及处理装置
近日,国家知识产权局公布专利“电力数据的处理方法及处理装置”,申请人为国网北京市电力公司。
本发明公开了一种电力数据的处理方法及处理装置。其中,该方法包括:根据电流互感器采集到的供电线路上的电流值,得到第一图像,其中,电流互感器设置在供电线路上,进而根据插值法对第一图像进行处理,得到第二图像,进一步地,确定第二图像对应的电流值特征是否符合预设电流值特征,若第二图像对应的电流值特征不符合预设电流值特征,则发送告警信息,其中,告警信息用于指示供电线路异常。
本发明解决了相关技术中无法规避散点图带来的信息缺失和图形畸变,进而不能准确的判断出任意时刻的地铁负荷特性的技术问题。
Transformer Internal Fault Detection based on Symbolic Dynamic
Li Tao Gao Xiao Chen Weijia
(The College of Information Science and Engineering of Hunan University, Changsha 410082)
As for condition based maintenance of transformers, this paper proposes a method based on symbolic dynamics to diagnose the state of transformer from extracting signal characteristics of the inter-turn fault. This method does not need external sensors, it can find potential transformer internal fault and severity quickly and efficiently. After modeling the internal fault of the transformer and get the primary side current data under this condition. Then Symbolic Dynamic is used to generate a sequence of symbols from the current data. According to the symbolic sequence, we set up the mechanism of signal difference measurement to analyze the data. The simulation shows that when the inter-turn short circuit fault becomes harder, differences can be detected promptly and effectively between signal and the normal signal according to the method. It provides a solid basis for condition based maintenance of transformers Moreover this paper test the Symbolic Dynamic method on the field test data of transformer internal fault. The result verified the validity of the Symbolic Dynamic on the detection of transform internal fault.
symbolic dynamic; transform internal fault; maximum entropy based partitioning;markov state matrix
国家杰出青年科学基金(50925727)
湖南省科技计划项目(2010FJ3035)
李 涛(1974-),男,湖南邵阳人,副教授,研究方向为智能电网、电路设计、电气设备风险及可靠性等方面。

