An Indoor Localization Algorithm with Unknown Transmission Power for Wireless Sensor Network*

XU Kun，LIU Hongli，MA Ziji，HU Jiusong（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）



An Indoor Localization Algorithm with Unknown Transmission Power for Wireless Sensor Network*

XU Kun，LIU Hongli*，MA Ziji，HU Jiusong
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

Unknown transmission power is to degrade the accuracy of positioning in received signal strength-based in⁃door localization.To solve this problem，we propose a novel localization algorithm based on received signal strength indicator gathered from real indoor environment.The proposed algorithm regards transmission power as nuisance pa⁃rameters estimated along with source locations and transforms the traditionally nonlinear localization problem into a linear optimization problem using linear approximation which can be solved very efficiently.We apply the least squares to solve the corresponding localization problem.Simulation and experimental results show that the proposed algorithm achieves high performance compared to traditional algorithms when the transmission power is unknown.

wireless Sensor network；localization；received signal strength；transmission power

无线传感网络［1］WSN（Wireless Sensor Network）是一种新兴的信息采集和处理技术［2］，在环境监测［3］、战场监控［4］、家庭医疗监护［5］和交通流量监测［6］等相关领域具有广阔的应用前景。在基于WSN的各种应用中，节点定位技术［7］是无线传感网络的关键技术之一，是实现路由、追踪等网络其他功能的基础。

基于接收信号强度指示值［8］RSSI（Received Sig⁃nal Strength Indicator）的定位技术由于实现简单、无需增加额外的硬件设施，近几年得到了很多研究者的关注。文献［9］通过分析多径效应和外部干扰对RSSI的影响，提出采用频率分割集来克服多径效应RSSI的影响，通过改善RSSI的测距精度来提高定位的精度。文献［10］根据实验采集到的RSSI测量值，通过动态计算信号传输模型中的参数，提出了一种自适应的定位算法，该算法可以有效的抵御环境变化对RSSI测量值的影响。文献［11］将基于RSSI的定位问题表示成一个求最大似然的数学问题，通过迭代的方法估算出了未知节点的坐标；文献［12］将定位问题表示成一个求最小二乘的问题，并求出了对应的未知节点坐标。目前，虽然提出了很多基于RSSI的定位方法，但是，这些方法都假设已经提前预知了发射功率［13］大小，很少有文献考虑发射功率未知的情况。

在实际的应用中，由于传感节点一般是随机部署在监测区域内，并不能保证所有的传感节点都提前知道发送节点的传输功率。而且由于传感节点是电池供电的，随着节点的使用，电池的电量会慢慢降低，节点的发射功率也会发生变化。在本文中，考虑发射功率不能提前预知的问题，根据室内环境中RSSI的变化，提出了一种新的鲁棒的室内定位优化算法。用对数-正态衰减模型表示室内信号的传输信道模型，将发射功率看成一个未知的变量，通过消去公式中的对数符号，将一个多参数的定位问题进行简化，采用最小二乘法得出了未知节点的坐标。通过仿真和实测实验证明了提出算法能够得到很好的定位精度。

1　问题分析

考虑在一个二维空间ℝ2中，存在一个由N个信标节点和1个目标节点组成的网络，其中N个信标节点的位置已知：xi=［xi，yi］，i=1，2，…，N。目标节点的位置未知：x=［x，y］。信标节点i以功率P向监测区域广播无线信号，目标节点接收到信标节点发送的信号后进行定位。可以将每个节点接收到的信号强度用对数-正态衰减模型表示为：

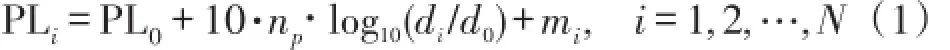
其中，PLi表示传感器节点i与目标节点之间距离为di时的真实路径信号衰减值，单位为dBm；PL0表示参考节点与目标节点距离为d0时的参考路径信号衰减值；di=||xi-x||2表示传感器节点i与目标节点之间的欧氏距离；d0表示参考节点和目标节点之间的欧氏距离，一般设为1 m；np表示路径衰减因子，其值随环境而变化；mi表示一个对数正态的遮蔽效应，它是一个均值为0，方差为的高斯噪声。

通过式（1），可以将距离为di时接收到的信号强度值Pi表示为：

其中，Pt表示发射节点的发射功率，则可以将在参考距离为d0处的接收功率P0表示为：

因此可以将式（1）进一步表示为：

目前，很多提出的算法都是假设提前知道发射功率大小而提出的，但是，在实际应用中，由于节点部署的方式和使用过程中存在的电量损耗，不可能提前预知发射功率的大小。采用假设发射功率已知的方法，会给节点的定位带来额外的定位误差。

为了体现不同发射功率下，节点接收到的接收功率差异情况。在一个室内环境中，部署了20个传感器节点，在每次实验时，都给节点设置不同的发射功率，并记录不同发射功率下，距离为1 m时的接收功率大小，通过对每次测试进行100次同样的实验，对接收到的RSSI值取平均值，相应的测试结果如表1所示。

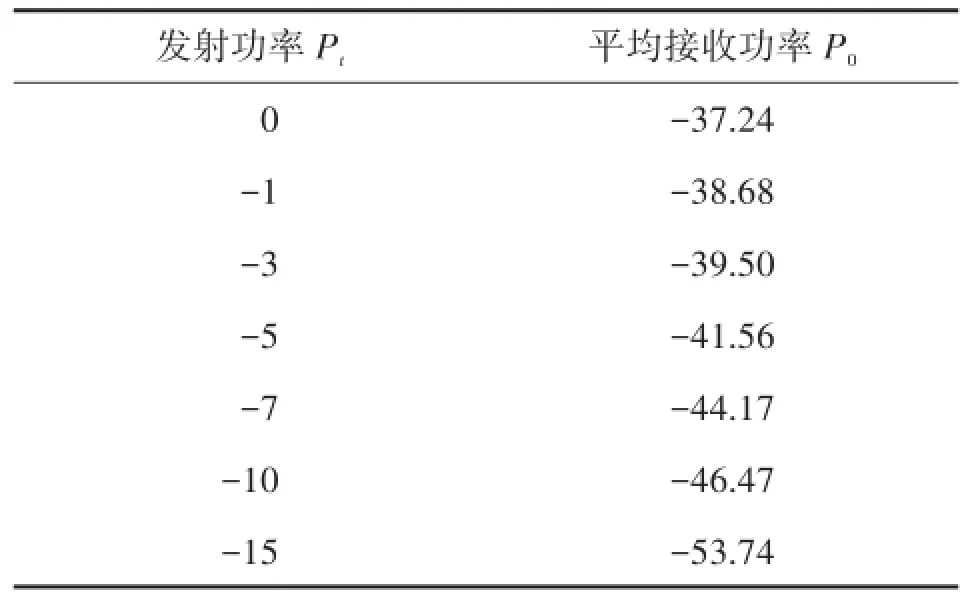
表1　不同发射功率下，距离为1 m时平均接收功率单位：dBm

从表1可以看出，当发射功率不同时，P0的值存在较大的差异，发射功率越小，两者之间的差异越大，其最大差值可以达到16 dBm。

2　针对发射功率未知的定位算法

为了减少发射功率未知情况下所带来的定位误差，针对前面提出的系统模型，将式（4）中的P0看成一个未知变量参与到目标节点的定位中来，其目的是，根据已知的接收功率Pi和信标节点的坐标xi，求出目标节点的坐标x。通过对式（4）进行移项可得：

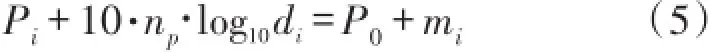
对式（5）的两边同时进行除以5np的操作，可以得到：

在式（6）中，由于存在对数项，为了消除对数项对公式的影响。通过变形，可以将其进一步简化为：

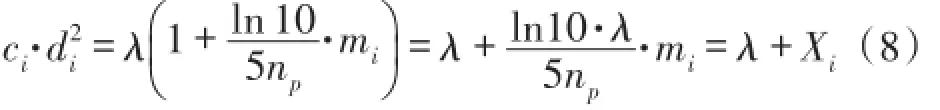
其中，令Xi=，它表示一个均值为0，方差为的高斯随机变量，令σi=可以将其简化为：Xi∼N（0，σi）。

通过最小二乘法，可以求出未知变量的解：

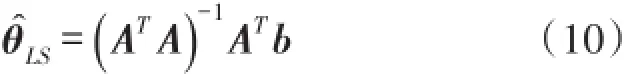
通过以上的分析，可以得出如下的定位流程：①目标节点x广播一个信标报文，提出定位请求；②临近的信标节点接收到定位请求后，发送应答帧；③目标节点从接收到的应答帧中提取出对应的信号强度值RSSI和信标节点的位置信息；④目标节点将接收到的每个信标节点发送的信号强度值RSSI存入数组，当达到一定阈值后求平均值；⑤当目标节点接收到多个信标节点的平均信号强度值RSSI后，联合信标节点的位置信息，采用提出的定位算法估算目标节点的位置信息。

通过线性逼近后，定位问题被转化为一个线性问题，可以有效的降低定位过程中的计算复杂度。接下来，对提出算法和ML算法、LS算法的计算复杂度进行比较。ML算法是非线性和非凸的，它的计算复杂度主要取决于求解的方法和迭代次数。当采用高斯牛顿法求解时，其对应的计算复杂度为O（KN3），其中K表示迭代次数；由于提出算法和LS算法最后都利用最小二乘法对问题进行求解，所以两种算法的计算复杂度都近似表示为O（34N）。

3　仿真和性能分析

为了验证提出算法在室内环境中的定位性能，分别基于仿真环境和实测环境对提出的算法进行了分析。假设估算得出的目标节点的坐标为（x̂，ŷ），对应的真实坐标为（xtrue，ytrue），则定义相应的均方根定位误差为MMSE=

3.1仿真

考虑一个20 m×20 m大小的区域进行仿真，在该区域内随机部署20个信标节点，信标节点的位置是已知的。一个目标节点随机的部署在测试区域内。我们在一台CPU为Intel Core i5、主频为3 GHz，内存大小为4 GB、1 600 MHz DDR3的台式机，针对每个算法进行500次仿真实验。为了模拟环境的真实性，在生成的RSSI信号中添加了均值为0，标准差为0.5的高斯随机噪声。对于提出的算法，每一次仿真实现，发射功率P0会在区间［-55，-25］之间进行选择。

图1针对发射功率未知的情况，比较了提出算法和传统的ML算法以及LS算法的定位精度。在实验中，我们假设ML算法和LS算法都提前知道功率P0的大小，其值设为-35 dBm。而实际上，P0的功率是未知的。从图中可以看出，当发射功率未知时，采用传统的ML算法和LS算法，在实际发射功率和预知发射功率存在偏差时，目标节点的定位误差会变大，而且，随着两者之间的差距越来越大，其对应的定位误差会明显增大。这是因为随着RSSI测量值的增大，对测距也变得越来越敏感，在RSSI超过-50 dBm后，1 dBm的差距就会带来较大的测距误差，从而对定位性能带来较大的影响。提出的算法因为考虑了功率未知的问题，其定位精度明显优于传统的定位算法，尤其是预知功率和实际功率之间的差异较大时，其定位性能尤其明显。

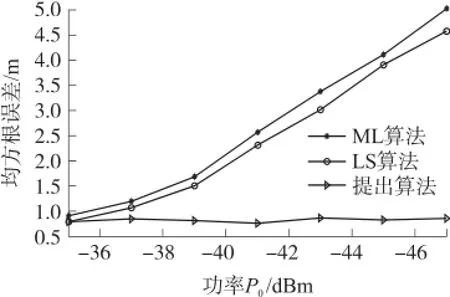
图1　不同算法在未知功率下的定位误差

图2显示了提出算法在存在两个信标节点的发射功率未知，且与其它信标节点的发射功率不同时，不同定位算法的定位精度和信标节点个数之间的对应关系。假设除了2个信标节点的发送功率和预设的功率不同外，其它信标节点的真实发送功率都和预设的功率相同。从图中可以看出，提出的算法的定位性能要明显优于传统的定位算法，因为提出的算法将发射功率作为一个未知参数，不会出现预设功率和发射功率不同所带来的测距误差。随着信标节点的增多，传统的定位算法的定位性能也跟着逐渐提高，这是因为只存在两个发射功率和预设功率不同的节点，随着信标节点数目的增加，两个发射功率不同的信标节点对定位所带来的影响被慢慢减少。

图2　不同定位算法在存在两个未知功率节点时的定位误差

3.2实测实验

我们在湖南省长沙市湖南大学的一个实验室进行了实测实验，目标节点和信标节点都采用一个CC2430的通信模块，工作频率为2.4 GHz，发送天线和接收天线都采用四分之一波长的全向天线。实验环境是一个5.9 m×3.7 m的实验室，里面有实验桌、椅子、空调等，其测试环境图如图3所示。在测试环境中部署了6个参考节点和一个目标节点，节点之间通过ZigBee协议组成一个自组网络。

图3　测试环境图

图4显示了在实测环境中，采用不同的定位算法得到的定位误差。

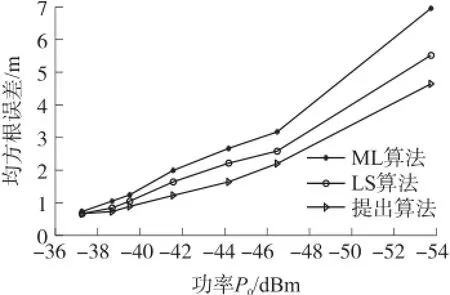
图4　室内环境下不同算法的定位误差

从图4可以看出，在真实的室内环境中，提出的算法的定位性能要明显优于传统的ML算法和LS算法。但是，通过和图1的仿真结果相比较，在真实的室内环境下，三种算法的定位性能都要明显差于仿真时的定位性能。这是因为，在真实的室内环境中，由于存在室内存在墙壁、桌子等障碍物的影响，实测环境要远比仿真环境复杂，无线信号会受到反射、折射、衍射等多径效应的影响。

4　结论

在基于RSSI的节点定位过程中，提出的许多基于RSSI的定位算法都假设提前预知了发射功率的大小。但是，由于网络部署和电池电量等因素的影响，发射节点向网络中传送的发射功率一般是无法提前预知的。针对发射功率未知的问题，提出了一种鲁棒的室内定位算法，通过将发射功率看成一个未知变量，通过对公式中的非线性项进行线性逼近，得到了一个新的定位公式，并通过最小二乘法计算出了目标节点的位置信息。真实实验和仿真表明，和传统的定位算法相比，提出的算法具有很好的定位性能。

［1］Athreya A P，Tague P.Network Self-Organization in the Internet of Tthings［C］//Sensor，Mesh and Ad Hoc Communications and Networks（SECON），2013 10th Annual IEEE Communications So⁃ciety Conference on.IEEE，2013：25-33.

［2］段翠翠，王瑞荣，王建中，等.基于无线传感器网络的高危生产区人员定位系统［J］.传感技术学报，2012，25（11）：1599-1601.

［3］Conti M，Willemsen J，Crispo B.Providing Source Location Priva⁃cy in Wireless Sensor Networks：A Survey［J］.Communications Surveys&Tutorials，IEEE，2013，15（3）：1238-1280.

［4］Demigha O，Hidouci W K，Ahmed T.On Energy Efficiency in Col⁃laborative Target Tracking in Wireless Sensor Network：A Review［J］.Communications Surveys&Tutorials，IEEE，2013，15（3）：1210-1222.

［5］孙启永，张文，李海波，等.基于微电极阵列和无线传感器网络的水环境重金属检测系统研究［J］.传感技术学报，2013，26（7）：907-911.

［6］Li K，Bigham J，Bodanese E L，et al.Outdoor Location Estimation in Changeable Environments［J］.Communications Letters，IEEE，2013，17（11）：2072-2075.

［7］王千，金光，钮俊.一种基于RSSI的混合定位算法［J］.传感技术学报，2015，28（12）：1823-1829.

［8］Malajner M，PlaninšicˇP，Gleich D.Angle of Arrival Estimation Us⁃ing RSSI and Omnidirectional Rotatable Antennas［J］.Sensors Journal，IEEE，2012，12（6）：1950-1957.

［9］Mraz L，Cervenka V，Komosny D，et al.Comprehensive Perfor⁃mance Analysis of ZigBee Technology Based on Real Measure⁃ments［J］.Wireless Personal Communications，2013，71（4）：2783-2803.

［10］Ahn H S，Yu W.Environmental-Adaptive RSSI-Based Indoor Lo⁃calization［J］.IEEE Transactions on Automation Science and En⁃gineering，2009，6（4）：626-633.

［11］Salman N，Ghogho M，Kemp A H.On the Joint Estimation of the RSS-Based Location and Path-Loss Exponent［J］.Wireless Com⁃munications Letters，IEEE，2012，1（1）：34-37.

［12］So H C，Lin L.Linear Least Squares Approach for Accurate Re⁃ceived Signal Strength Based Source Localization［J］.IEEE Trans⁃ actions on Signal Processing，2011，59（8）：4035-4040.

［13］Mouhtaropoulos D，Boursianis A，Samaras T.Prediction of Trans⁃mission Path Loss in Indoor Environments with The Radiosity Method［J］.Microwave and Optical Technology Letters，2013，55（10）：2401-2405.

徐琨（1979-），男，湖南津市人，湖南大学博士研究生，研究方向为无线传感网络定位和安全，kunxuhnu@sina.com；

刘宏立（1963-），男，湖南常德人，湖南大学教授，博士生导师，研究方向为无线传感网络、移动通信系统与软件无线电、智能信息处理与传输技术，hongliliu@hnu. edu.cn。

EEACC：6150P10.3969/j.issn.1004-1699.2016.06.021

一种针对未知发射功率的室内定位优化算法*

徐琨，刘宏立*，马子骥，胡久松
（湖南大学电气与信息工程学院，长沙410082）

在基于接收信号强度的室内定位中，未知的发射功率会降低网络的定位性能。为了解决这一问题，根据室内环境中接收信号强度的特性，提出了一种新的的室内定位优化算法。该算法将发射功率表示成一个未知变量，通过将公式中的非线性项进行线性逼近，将非线性的定位问题转化为一个线性优化问题，并采用最小二乘法求出目标节点的坐标。仿真和实验结果表明，在发射功率未知的情况下，提出算法要明显优于传统的定位算法，具有很好的定位性能。

无线传感网络；定位；接收信号强度；发射功率

TP393

A

1004-1699（2016）06-0915-05

2015-10-22修改日期：2016-02-01

项目来源：国家自然科学基金面上项目（61172089）；中央国有资本经营预算支出项目（财企［2013］470号）；博士后基金面上项目（2014M562100）；湖南省科技厅项目（2014WK3001）