Error Analysis of FBG Sensors Bonded on LowModulus Host Materials*

WU Rujun，SUN Dianliang（1.Shanghai Dianji University，Shanghai 01306，China；.Shandong P&T Engineering Co.，LTD，Jinan 50001，China）



Error Analysis of FBG Sensors Bonded on LowModulus Host Materials*

WU Rujun1*，SUN Dianliang2
（1.Shanghai Dianji University，Shanghai 201306，China；2.Shandong P&T Engineering Co.，LTD，Jinan 250001，China）

FBG sensor has been widely used in measuring the strain of host material.The existing of FBG sensor af⁃fects strain distribution of the host material，and the host material does not contact the optical fiber.However，may result in a decrease of strain measurement accuracy.So，the strain relationship between the optical fiber and host material was needed to study to improve the measurement accuracy.A theoretical model of strain transfer was devel⁃oped to include the influence of FBG sensor.Subsequently，the theoretical predictions were validated by finite ele⁃ment analysis.The effect of parameters on strain transfer rate was discussed according to the current theoretical analysis.the error between theoretical solution and FEA was controlled within 3%.The theoretical model satisfied accuracy requirement of the FBG sensors，which is considered as a guidance for its practical application。

Fiber Bragg Grating（FBG）；strain transfer rate；theoretical analysis；shear stress

与传统电阻传感器相比，光纤布拉格光栅（FBG）传感器具有体积小、质量轻、抗电磁干扰等众多优点。根据安装方式的不同，可以分为表面粘贴式和埋入式两种，但是无论哪一种安装方式，测量应变和真实应变存在一定的误差，为进一步提高测量精度，建立测量应变与真实应变之间的关系至关重要［1］。

国内外众多学者针对该问题作了研究，Ansari等［2］假定光纤中心处的应变和基体应变相同，从而得到FBG传感器的应变分布规律。Duck G等［3］利用傅里叶变换得到光纤应变与基体应变之间的关系。李东升等［4-6］首次提出FBG传感器各层应变率相等的假设，得到更高精度的应变传递理论。周智等［7］假定各层中点处应变相等，进而得到光纤应变与基体应变之间的关系。Zhao等［8］对四层表面粘贴式FBG传感器应变传递理论进行了研究，得出各层应变分布规律。Wang等［9］对表面式FBG传感器应变传递问题进行了研究，得到与李东升等人相似的结论。Her和Huang［10］针对表面粘贴式FBG传感器应变传递问题进行了相关研究。Moradi M［11］建立了粘贴于薄板上的传感器测量应变与薄板应变之间的传递理论。Wu等［12］人研究了埋入式FBG传感器与基体之间的耦合作用；吴入军等［13］首次提出多项式形式的剪应力表达式，基于此建立应变传递方程，经验证具有较高精度。王花平等［14］针对纯沥青包裹的FBG传感器结构进行应变传递理论分析和实验验证工作。金秀梅等［15］推出了裸光纤、涂覆层和基体的剪应力在径向的分布，并通过有限元进行了验证。

虽然国内外学者进行了诸多相关研究，但是大多研究都是基于基体承受均匀应变状态，忽略传感器的存在对基体应变的影响，这在基体刚度较小时会产生一定误差，因此本文充分考虑了FBG传感器与基体之间的耦合作用，利用平面应力理论建立了FBG传感器与基体之间的应变传递理论，研究光纤应变与基体应变之间的关系，将被测对象进一步扩展到刚度较小的基体。

1　理论推导

图1为安装结构示意图，该结构由光纤、保护层、粘结层、衬底、外粘结层和基体组成，基体在轴向（x方向）预应变为ε∞。在本节中将基于以下假设推导基体预应变与光纤应变之间的关系［2-13］。①所有的材料，包括光纤、保护层、粘结层、衬底和外粘结层都是线弹性材料。②所有的界面都是理想界面，即无相对滑移。③FBG传感器厚度很薄，忽略r方向的作用力。

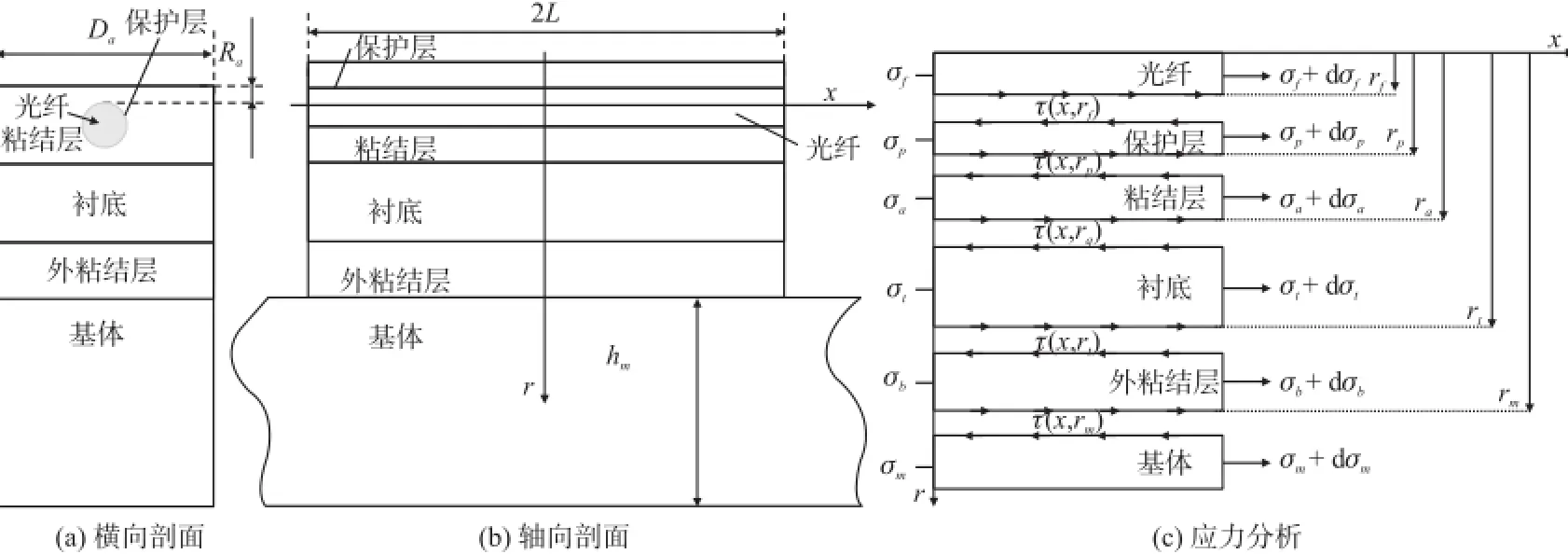
图1　传感器示意图

下标f，p，a，t，b和m分别代表光纤、保护层、粘结层、衬底、外粘结层和基体；E，G和λ分别代表弹性模量、剪切模量和泊松比；L，Ra，Da分别代表半粘结长度、粘结层上厚度和传感器宽度；2L为粘结长度；σ，τ，ε和γ分别代表轴向应力、剪切应力、应变和剪应变；rf代表光纤半径、r代表径向坐标量。

对光纤建立平衡微分方程：

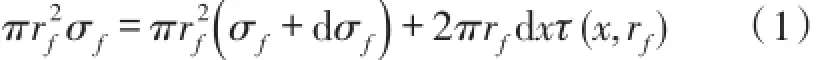
其中τ（x，rf）代表光纤和保护层界面上的剪应力。同理，保护层、粘结层、衬底和外粘结层的微分平衡方程为：

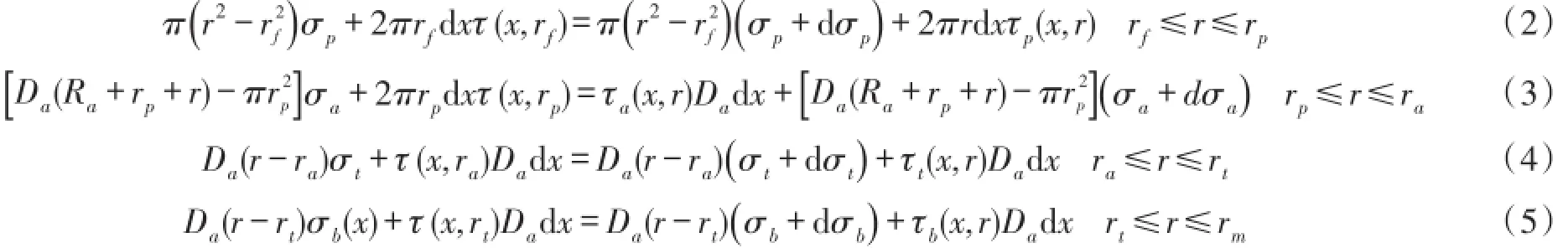
其中：τp（x，r）、τa（x，r）、τt（x，r）和τb（x，r）分别代表保护层剪应力、粘结层剪应力、衬底剪应力和外粘结层剪应力。

整理式（1）～式（5）并简化，得到保护层、粘结层、衬底和外粘结层剪应力：

李东升［4-6］等提出：因为光纤、保护层、粘结层、衬底和外粘结层是同步变形的，可以假设其x方向的应变梯度近似相同，即：存在式（7）：

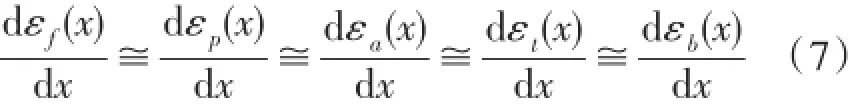
将式（7）代入式（6）并简化，得到各层结构剪应力与光纤轴向应变的关系为：

因为轴向变形是主要的变形，r方向变形是非常小的，忽略r方向变形［4-6，10-13］，所以存在式（9）：

其中，u和v分别代表x方向和r方向位移。将式（8）代入式（9）并且积分得到：

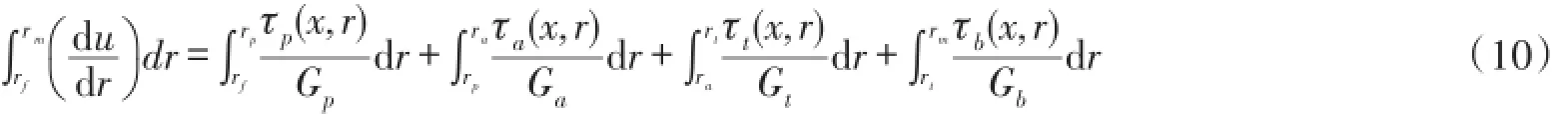
求解式（10）得到：

式（11）是基体轴向位移与光纤轴向位移之间的微分方程，参数k为：

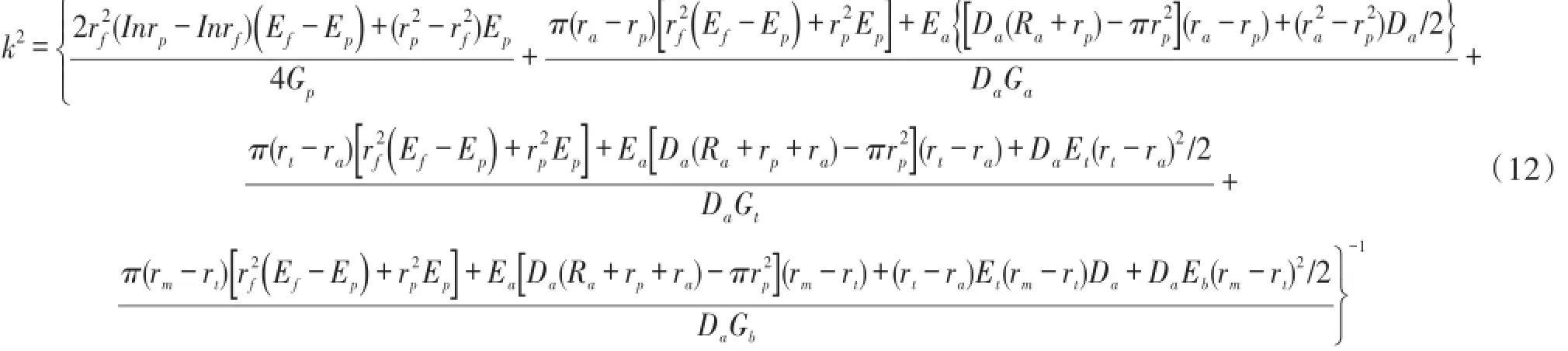
由于基体上表面所受剪应力为奇函数，所以存在σx和σy为偶函数，τxy为奇函数，设双调和函数通解［16］为：

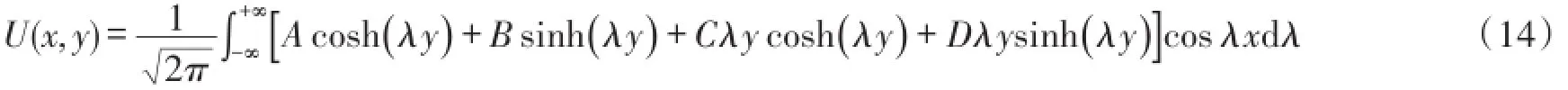
将式（11）对x求微分得到光纤应变的二阶微分方程（13）：

根据双调和函数（14），可以求得基体应力场表达式为［16］：

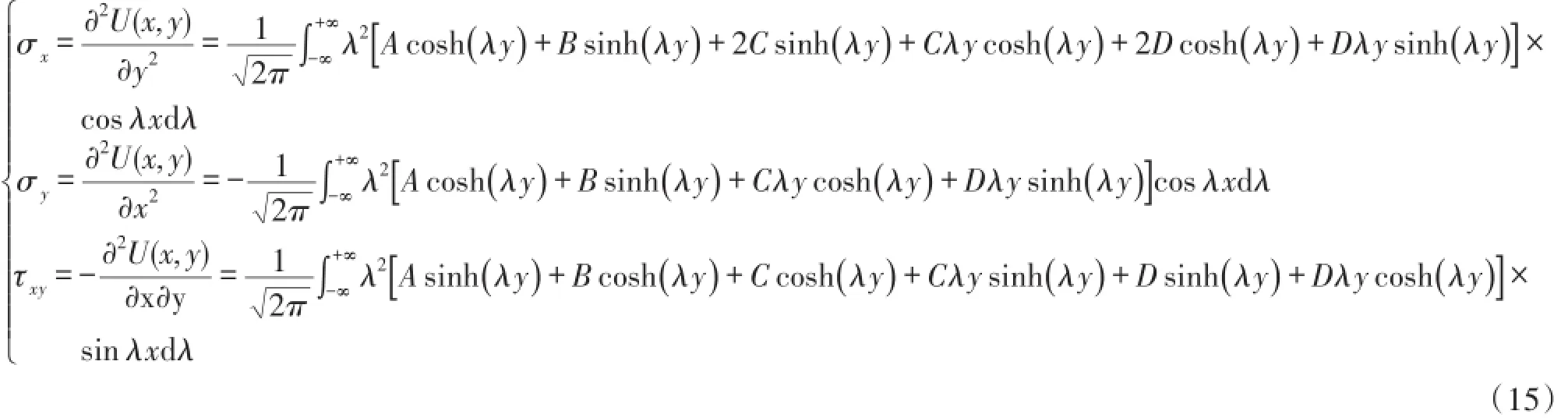
应力场式（15）满足基体下边界为自由表面，上边界受来自传感器的剪切力，如式（16）所示：

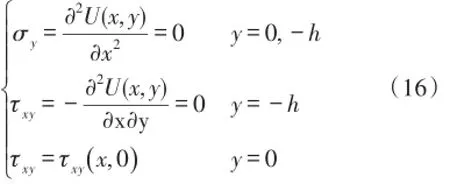
根据边界条件式（16）第1式和第2式带入式（15），求得各个系数为：

将（17）所示的参数带入到式（15）的第三式得到基体上边界的剪应力表达式（18）：

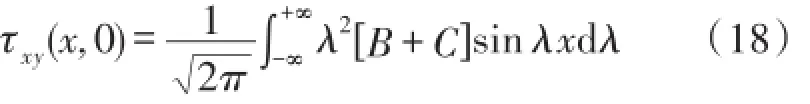
根据傅里叶变换与逆变换之间的关系将式（18）变形为：

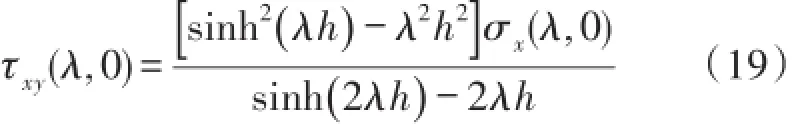
对式（19）进行整理、变形为：

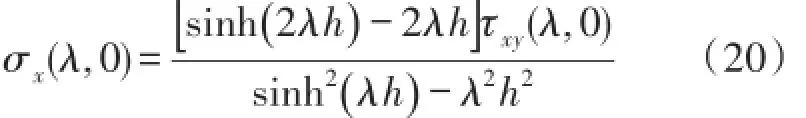
利用傅里叶逆变换可以得到基体在式（16）所示边界条件下，基体上边界轴向应变表达式：

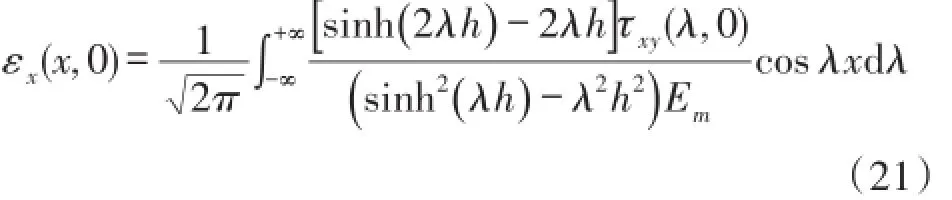
假定基体承受预应变ε∞，则基体上边界轴向应变如式（22）所示：

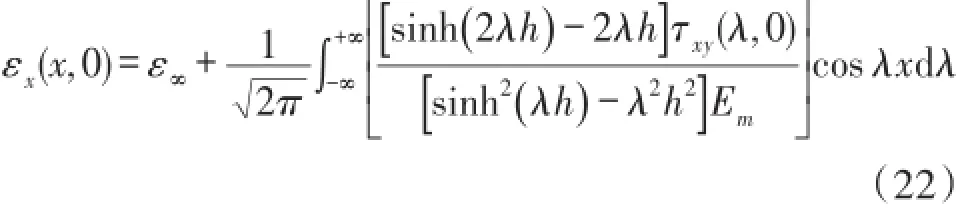
将式（22）带入式（13）得到：

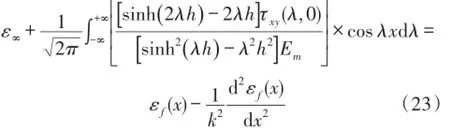
由式（8）可知基体上边界所受剪应力是具有对称性的面分布力，如式（24）所示：

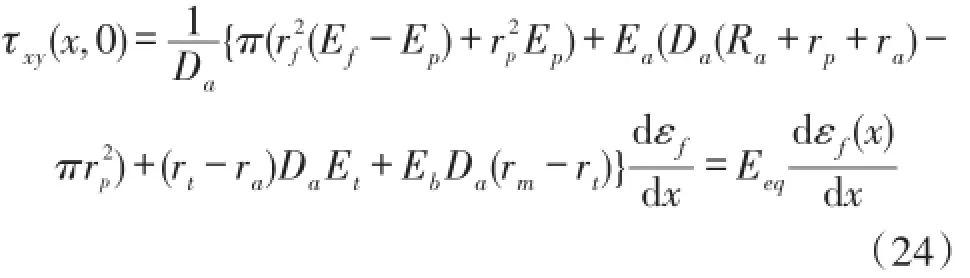
其中，Eeq定义为FBG传感器剪切刚度，利用式（23）和式（24）得到表达光纤应变与基体预应变之间的关系的二阶微分方程：

FBG传感器两端为自由面，存在以下边界条件［4-13］：

式（25）求解非常困难，对其进行适当简化得到：

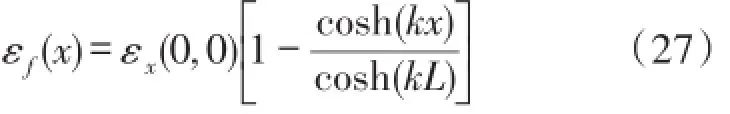
基体上边界承受的剪应力简化为：

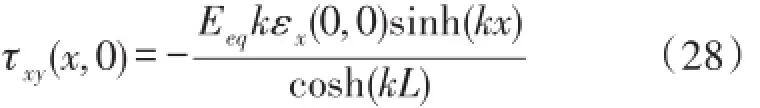
对式（28）进行傅里叶变换得到：

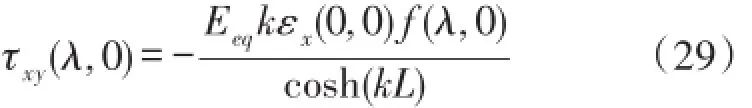
其中：

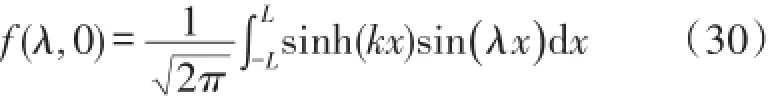
将式（27）和式（29）带入式（23）中得到式（31）：

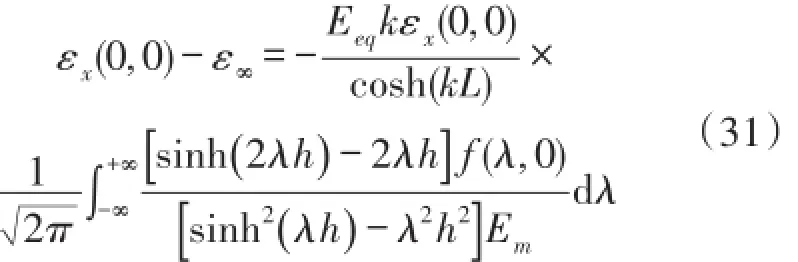
式（31）是关于εx（0，0）的线性函数，整理后得到基体原点处的轴向应变为：

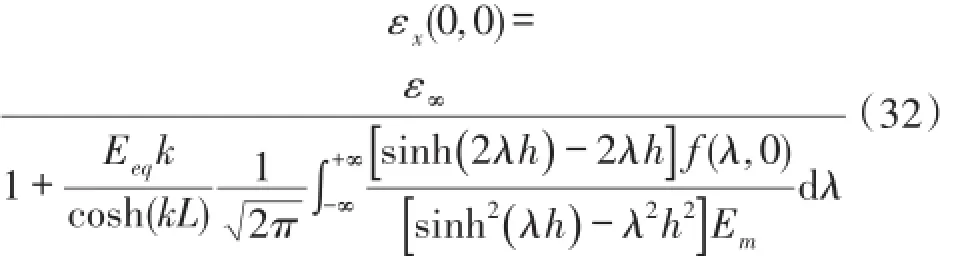
将式（32）带入式（27）中得到光纤应变与基体预应变之间的关系表达式，该表达式是关于轴向坐标x指数变化、与基体预应变ε∞成线性关系，同时与基体弹性模量、厚度等参数相关的函数。

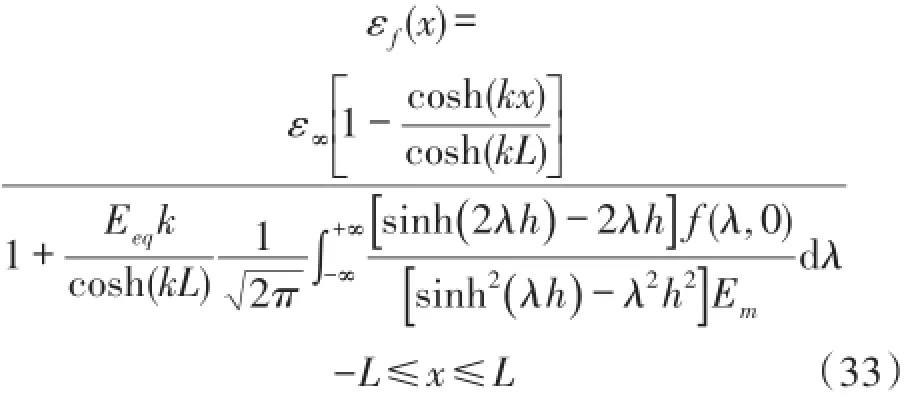
由式（33）可以得到光纤应变传递率为：

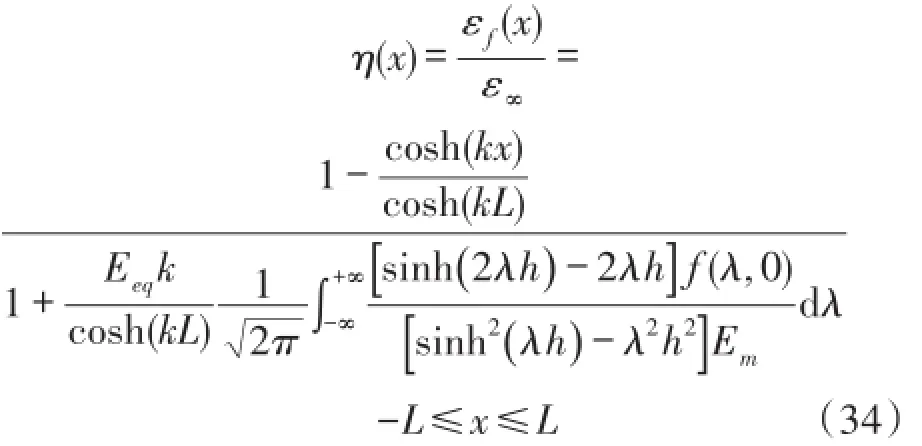
实际测量应变是光纤应变在轴向各点应变的平均值，因此对式（34）求其平均值得到FBG传感器平均应变传递率为：

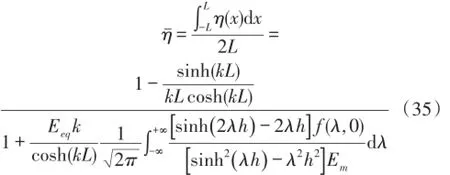
虽然本节利用傅里叶变换进行了直接求解，但是得到解析解仍非常困难，一般需要借助数值方法，将无限问题转化为有限域求其数值解。对方程（34）和方程（35）写成离散形式分别为式（36）和式（37）。

其中，L0为基体长度的一半，λn=nπ/L0，n=（1，2，3…）。方程（36）即为长度为光纤长度为2L，基体长度为2L0，厚度为h，在光纤轴向方向上的应变传递率，它是轴向坐标x的函数；（37）代表平均应变传递率，它反映FBG传感器的平均应变传递效果。

2　理论验证和参数分析

2.1有限元验证

利用有限元软件Ansys对本文理论进行验证。由于结构的对称性，在分析时候取一半进行分析，图2为有限元模型图，所使用材料物理参数如表1所示，其他参数为：rf=0.062 5 mm，rc=0.102 5 mm，ra=0.14 mm，rt=0.17 mm，rb=0.19 mm，L=20 mm，L0=60 mm，h=8 mm，基体弹性模量取4 000 MPa和6 000 MPa，对称面使用对称约束、端面使用位移边界条件来模拟预应变。

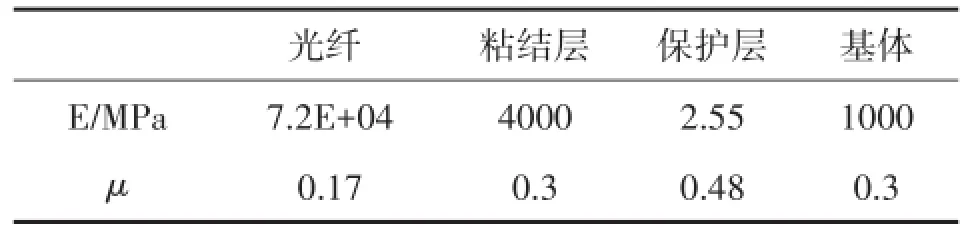
表1　各层物理参数

理论解是利用式（36）得到的，FEM解是利用软件Ansys得到的结果。图3为理论解和FEM解的对比，通过对比可知：根据理论解和FEM解误差非常小，基本控制在3%以内，且基体弹性模量对应变传递率是有影响的，基体弹性模量越大越应变传递率越高；在应变传递率光纤中间点最大，越接近两端越小，直到在两端减小为0。因此在设计FBG传感器时，可以在FBG传感器两端留一定的粘结余量，以提高测量的精度。

图2　有限元模型图

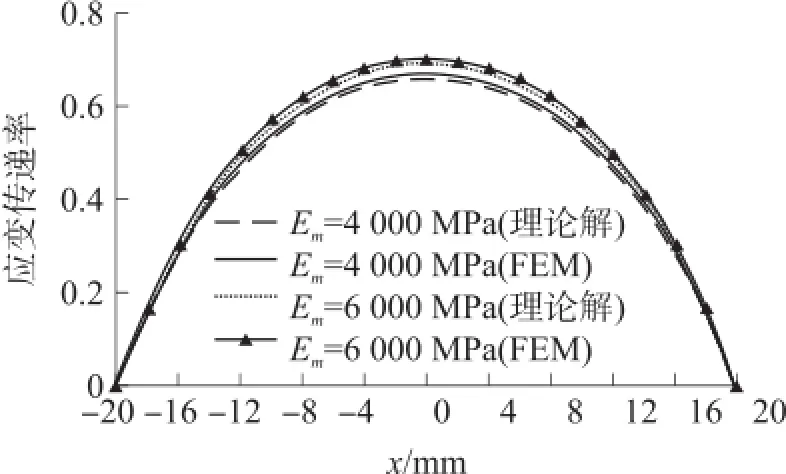
图3　理论解和FEM解得对比

表2为应变对比表，测量应变反映的是整个光纤各处应变的平均值，因此，FEM应变取整条光纤各处应变的平均值。由表2可知：FEM应变远远小于真实应变，必须进行修正，利用本文理论修正后的修正应变与真实应变误差在2%左右。因此，在实际测量时得到的测量应变也必须进行修正，以提高测量精度。

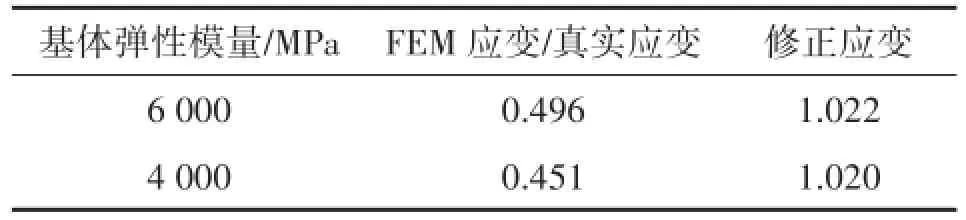
表2　应变比较

2.2参数分析

光纤光栅传感器材料参数见表1，图4和图5分别表示基体弹性模量分别为4 000 MPa、6 000 MPa和10 000 MPa时，厚度分别为8 mm、12 mm和20 mm时的应变传递率随FBG传感器轴向坐标变化曲线图。从图中可知：随着基体厚度和弹性模量的增加，应变传递率逐渐增加；厚度和弹性模量对应变传递具有较大的影响，随着基体弹性模量和厚度的增加，其对应变传递率的影响逐渐减小；最大应变传递率出现在中间，逐渐减小至两端为0。这是因为，随着基体厚度和弹性模量的增加，基体刚度也逐渐增加，传感器的存在对基体应变的影响逐渐减小。这一结论与一些文献中应变传递率随着基体厚度的增加而逐渐减小的结论相反，这是因为：本文理论是建立光纤应变与基体原有应变之间的关系，而现有大多数理论是建立光纤应变与粘贴传感器之后的基体应变之间的关系，两者有着根本的区别。

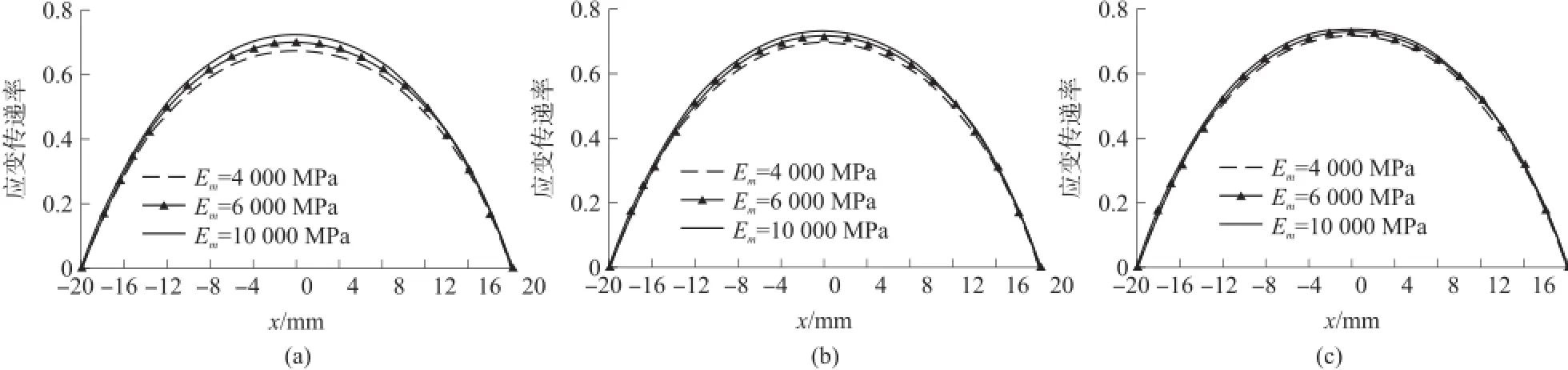
图4　h=8 mm、12 mm、20 mm时，基体弹性模量对应变传递率的影响

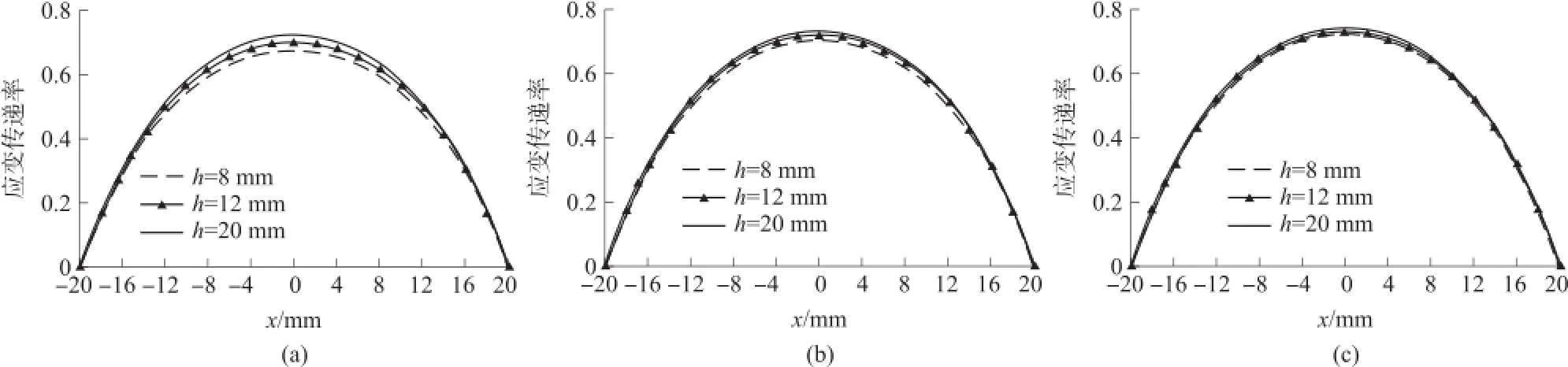
图5　Em=4 000 MPa、6 000 MPa、10 000 MPa时，基体厚度对应变传递率的影响

3　结论

本文针对低模量基体材料，建立了基体应变与测量应变之间的理论关系，充分考虑了基体和传感器之间的耦合作用，且FEM解和理论解的误差在3%以内，具有非常高的精度，经研究得出以下结论：①随着基体弹性模量和厚度的增加应变传递率均逐渐增大。②由于FBG传感器的存在，改变了基体应变分布，减小了基体应变，而且FBG传感器多层结构在应变传递过程中造成损失，因此在实际实际应变测量时，需要对测量应变进行修正。

［1］张自嘉.光纤光栅理论基础与传感技术［M］.北京：科学出版社，2009.

［2］Ansari Farhad，Yuan Libo.Mechanics of Bond and Interface Shear Transfer in Optical Fiber Sensors［J］.Journal of Engineer⁃ ing Mechanics，1998，12（4）：385-394.

［3］Duck G，Blanc M.Arbitrary Strain Transfer from a Host to an Em⁃bedded Fiber Optic Sensor［J］.Smart Materials and Structures，2000，9（4）：492-497.

［4］Li D S，Li H N.Strain Transferring of Embedded Fiber Bragg Grat⁃ing Sensors［J］.Smart Materials and Structures，2005，5765（1）：1085-1093.

［5］Li D S，Li H N，Ren L，et al.Strain Transferring Analysis of Fiber Bragg Grating Sensors［J］.Optical Engineering，2006，45（2）：02440.

［6］李东升，李宏男.埋入式封装的光纤光栅传感器应变传递分析［J］.力学学报，2005，37（4）：435-441.

［7］Zhou J，Zhou Z，Zhang D，et al.Study on Strain Transfer Charac⁃teristics of Fiber Bragg Grating Sensors［J］.Material Systems and Structures，2010，21（11）：1117-1122.

［8］Zhao H T，Wang Q B，Qiu Y，et al.Strain Transfer of Surface Bonded Fiber Bragg Grating Sensors for Airship Envelope Struc⁃tural Health Monitoring［J］.Journal of Zhejiang University-Sci⁃ence A（Applied Physics&Engineering），2012，13（7）：538-545.

［9］Wang Q B，Qiu Y，Zhao H T，et al.Analysis of Strain Transfer of Six-Layer Surface-Bonded Fiber Bragg Gratings［J］.Applied Op⁃tics，2012，51（18）：4129-4138.

［10］Her S C，Huang C Y.Effect of Coating on the Strain Transfer of Optical Fiber Sensors［J］.Sensors，2011，11（7）：6926-6941.

［11］Moradi M，Sivoththaman S.Strain Transfer Analysis of Surface-Bonded MEMS Strain Sensors［J］.IEEE Sensors Journal，2013，13（2）：637-643.

［12］Rujun Wu，Bailin Zheng，Kunkun Fu，et al.Study on Strain Trans⁃ fer of Embedded Fiber Bragg Grating Sensors［J］.Optical Engi⁃neering，2014，53（8）.

［13］吴入军，郑百林，贺鹏飞，等.埋入式光纤布拉格光栅传感器封装结构对测量应变的影响［J］.光学精密工程，2014，22（1），22-30.

［14］王花平，周智，刘婉秋，等.柔性基体材料封装FBG传感器的应变传递误差分析［J］.传感技术学报，2015，28（4）：492-497.

［15］金秀梅，杜建华，彭彦斌.埋入被测结构体内涂覆光纤传感元的应变传递特性研究［J］.2008，21（9）：1650-1653.

［16］吴家龙.弹性力学［M］.上海：同济大学出版社，1993.

吴入军（1979-），博士，上海电机学院讲师，主要从事工程力学、数值模拟和光纤传感方面研究，wurujunwurujun@ 163.com。

EEACC：0220；7230E10.3969/j.issn.1004-1699.2016.06.013

安装于低模量基体的FBG传感器误差分析*

吴入军1*，孙佃亮2
（1.上海电机学院，上海201306；2.山东省邮电工程有限公司，济南250001）

FBG传感器广泛应用于基体结构的应变测量，由于FBG传感器的存在改变了基体的应变分布，光纤与基体并非直接接触，导致测量应变产生一定的损失，因此需要研究光纤应变与基体应变的关系用以提高测量精度。建立了一个FBG传感器应变传递模型，并利用有限元验证其正确性，利用文中理论对各个参数对应变传递率的影响进行详细的分析；理论解和有限元解误差在3%以内。本文理论满足FBG传感器精度要求，对其实际应用具有一定的指导意义。

光纤布拉格光栅（FBG）；变传递率；理论分析；剪应力

TN253；O39

A

1004-1699（2016）06-0865-07

2015-12-22修改日期：2016-02-25

项目来源：国家863计划项目（2012AA040106）