大学物理教材及教学应重视刚体定轴转动时角动量与角速度的方向关系

周雨青（东南大学物理系，江苏南京 211189）

大学物理教材及教学应重视刚体定轴转动时角动量与角速度的方向关系

周雨青
（东南大学物理系，江苏南京 211189）

大学物理教材及教学在刚体定轴转动一章中，往往不太重视刚体总角动量与角速度的关系，而只关注于沿轴向的角动量，有时甚至出现L=Jω这种容易误解的表述形式.实际上，一般情况下刚体定轴转动时的角动量与角速度方向不相同，且刚体匀速转动时受变外力矩作用.本文首先从理论层面上给出角动量与角速度方向不一致的一般性证明，并给出方向相同的两种特殊情况，其次用一个实例阐述刚体定轴转动时，刚体轴受到垂直于轴向的变力矩作用，最后将特例所得结论推广至一般刚体定轴转动，从而阐明重视两者方向关系的必要性.

刚体；定轴转动；角动量；角速度；方向；变力矩

大学物理教材及教学一般不重视刚体定轴转动的总角动量与角速度的关系——即便是提到［1］也没有深入讨论其对转动的影响是什么.可能的原因是，第一，只有轴向角动量才是定轴转动的主体；第二，教学要求的难度和教学时数的有限对此问题的阐述带来的限制；第三，其他.可是正因如此教材以及教学中往往忽视了这两者的关系，甚至有些教材［2，3］在描述刚体定轴转动一章中会出现L=Jω的公式，这容易造成定轴转动刚体的角动量与角速度方向一致和匀速转动时不受外力矩作用的模糊结论.这个结论源于我们的大学物理教材通常在研究刚体定轴转动时，选取了一个垂直于转轴的xy参考平面［2］，并认为“这个参考平面内的质元的运动情况可以代表整个刚体的各质元的运动情况”，由于在这个参考面内的刚体质元只有相对于转轴方向的角动量，从而当推广至整个刚体，且又没有特别说明，由此产生L=Jω的误解，正是这个简化掩盖了刚体角动量与角速度方向不一致的结果.

1　刚体定轴转动时角动量与角速度方向不相同的一般性证明

在定轴转动的刚体上选一xy面，即参考面，转轴为z轴，如图1所示.

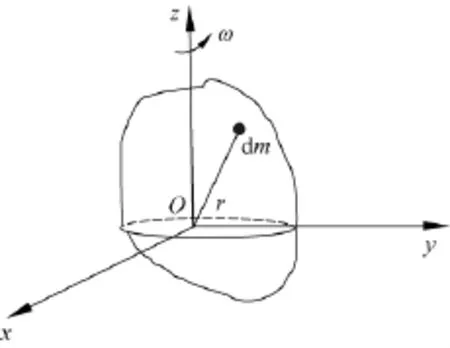
图1　定轴转动刚体示意图

由质点角动量定义L=r×m v，以及质点速度与角速度关系v=ω×r和ω=ωk可知，刚体上任意一点的质量元的角动量为考虑到r2=x2+y2+z2，r=x i+y j+z k，代入上式得

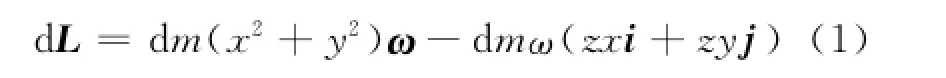
对式（1）积分可得刚体定轴转动的角动量为

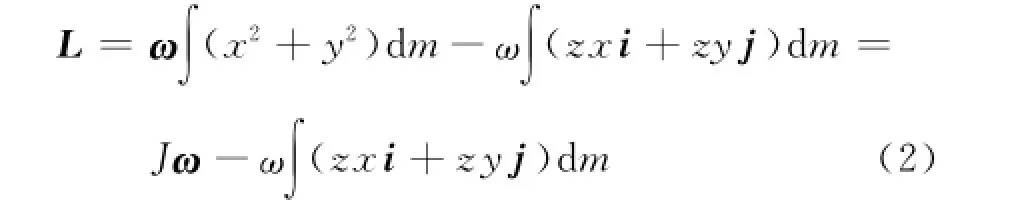
其J即为刚体相对于转轴z的转动惯量，由式（2）可见，一般的刚体的定轴转动角动量有两个分量，一个是沿转动轴方向，与角速度方向一致.另一个在x y平面内，方向随刚体转动而变化.

2　两种特例

（1）当刚体恰好就是参考面的“薄刚体”z=0时，式（2）变为

我们的教材往往就是从对参考面得出的这个结论，直接推广到了整个刚体.

（2）当刚体具有z轴对称，且取z轴为转动轴时，式（2）中的第二项积分为零，则式（2）也变为式（3）.

除上述两种情况之外，一般刚体的定轴转动角速度都不与角速度方向相同.因此大学物理教材上不宜将角动量与角速度之间的关系写作式（2）的形式，那样容易产生极大的误解.最好写作

以明示刚体角动量的z轴分量.那么，大学物理教学或教材中有必要说明式（2）的必要性吗？

3　明示刚体定轴转动时角动量与角速度方向不一致的必要性

首先，这两者是不同物理量，方向问题本就应该明确，且在大学物理层面上说清这个问题并不复杂，如式（2）的推导过程.

其次，若对两者方向关系不明示，将引起困惑，我们来看下面一个例子：

将长为R、质量可忽略的轻质杆连同质量为m的小球固定于竖直轻质轴上，构成一简单刚体，此刚体绕竖直轴做匀角速度ω转动.设固定竖直轴的两轴承各自到小球圆轨道平面中心的距离皆为a.选如图2所示的坐标系，求此刚体对转轴的角动量以及所受的外力矩.

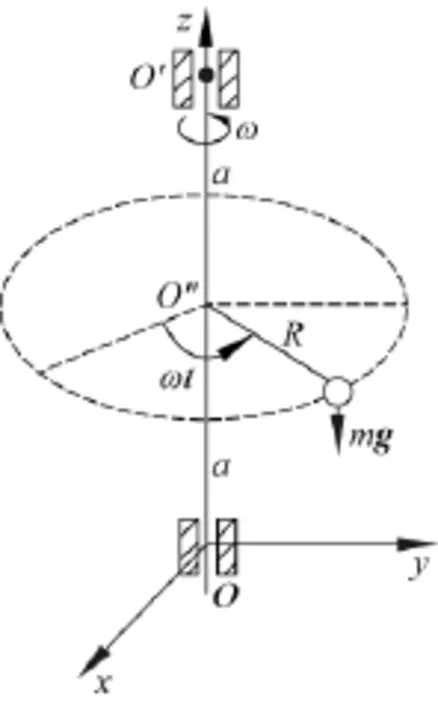
图2　绕竖直轴转动的杆

此例实际上就是一个“薄刚体”，但即便如此，若参考面并不取在“薄刚体”面内，角动量仍不是式（3）形式.

该问题的前一解似乎非常简单，无论是正确理解定轴刚体角动量（式（2）），还是错误理解（式（3）），都可以得出Lz=Jzω=mR2ω的结论.但是，对于后一问，如果错误理解刚体角动量只沿z轴方向，即L=Jω，则由于M==0，那么对求外力矩这一问题就会感到非常困惑——“不就是等于零吗？”.反之如果知道刚体定轴转动的角动量为式（2），则由于式（2）中的第二项分量是随刚体转动的，则刚体受到外力矩的作用就一点也不奇怪了.实际上，在图2所示的坐标系中，由于这个简单刚体系统的质量集中在小球——质点上，且质点在z=a的平面上作半径为R的匀速圆周运动，即式（2）中的坐标分别为

且不用计算积分关系.则方向沿刚体圆周运动的切线方向，这个外力矩只可能来自两轴承端在xy面内给予刚体的分力和小球所受的重力，见图3.这个力矩的作用使小球系统在x y面内的角动量分量产生转速为ω的进动，同时保证刚体的定轴取向不变.所以刚体定轴转动问题如果不阐述清楚角动量和角速度的方向问题，将会导致错误和困惑.

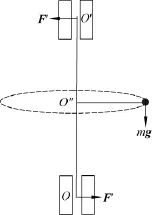
图3　轴承分力示意图

最后，弄清此类问题有助于理解大学物理演示实验中的若干问题，比如手持电筒式驻波演示仪的钢片振动原理、偏心弹簧振子转动与振动转换演示仪工作原理等.

综上所述，我们的大学物理教材和教学都应该，也必须重视刚体定轴转动时角动量与角速度的方向关系.

4　不同坐标系中看待同一问题的自洽性

上述范例中，若将坐标系取在刚体小球系统平面上，即刚体恰好就在参考平面内，满足特例情况（1）.由于z=0，刚体角动量的确为L=Jω，其中J=mR2.此时虽然有M==0，但疑惑并没解除，因为毕竟重力的力矩是明显存在的

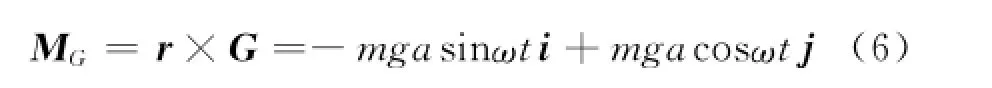
在大学物理教材中这个与参考面垂直的力往往被认为不影响转动而忽略的［1：109］，可它实际上是有物理效应的.正因为这个重力力矩的存在，导致轴承对转动轴有相互作用，我们可以根据力矩关系及其式（5）分别求出轴承O′和O处对轴的作用力F′和F.以O为坐标原点时，有

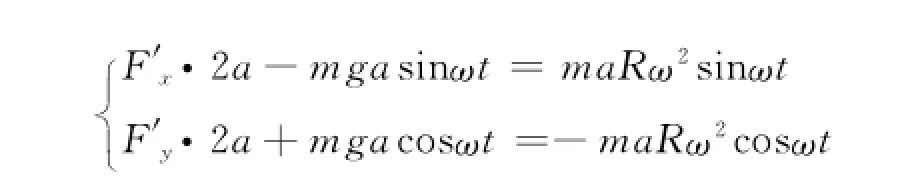
得

以O′为坐标原点（注意，此时z=-a）时，有

得

当以刚体小球系统平面为xy面时，由式（7）、（8）计算两轴承处的受力对O″的力矩恰好等于重力的力矩

5　简单刚体的应用及进一步讨论

由式（7）或式（8）可见，轴承施力或受力是周期性的，当我们在一个小电动机轴心上引出一个刚体小球，并将电动机固定在手持电筒式驻波演示仪的钢片上，电动机以ω匀速带动“偏心”小球转动时，钢片就将受到相同周期性的作用力而振动，这正是该演示仪重要的振动来源.这恰恰正是由于“偏心”小球的存在使得偏心轮转动时角动量与角速度方向不同造成的结果.

若在上述刚体系统中再加上一个质量相同、对称于转轴的另一个小球，构成对称简单刚体系统，则由于总存在（x、-x）和（y、-y）运动位置，所以依据式（2）可知，无论坐标原点选在转轴上的哪个位置，刚体角动量皆为L=J′ω，因而总力矩始终等于零.由于两边重力矩相互抵消，所以轴在水平面内不受力.这时的刚体才真正地满足L= Jω.这是一种动平衡状态，即使此时没有轴承的存在，转轴的取向也不会改变.同时由于质心在转轴上，总力矩又始终等于零，则当在与小球运动平面垂直，即平行于转轴方向上所加的任何外力，都将被轴承中出现的力抵消一切效应.

6　一般结论和对教学的建议

推而广之，当一般刚体的质量分布相对于转轴（z轴）来说对称时，刚体的角动量方向与角速度方向严格一致——沿z轴方向，即L=Jω.可以证明上述简单对称刚体系统的结论都能在对称刚体的定轴转动中成立.这种情况下才真正能忽略平行转轴方向的所有力的作用.

大学物理层面上要特别说明上述内容的确存在认知和要求上的难度，如何在不增加两难的情况下保证逻辑和系统上的清晰性？我们的建议是，第一，教材在不做大的变动下，可在本节内容开端首先明确说明：“刚体的定轴转动的角动量方向一般不与角速度方向相同，以下只讨论刚体角动量沿定轴方向的分量”.有了这样的表述，上文提到的“选择某一参考平面，其中的质元运动情况代表了其他刚体部分的运动情况”就不会引起歧义和错误了，大家都知道是指对旋转轴而言的.第二，教学中用偏心马达演示定轴转动引起振动的例子，说明角动量与转速方向不一致时引起的后果.这样学生尽管没有深入了解定轴转动的刚体总角动量与角速度的关系，但也不会混淆总量与分量的区别.

［1］ 陆果.基础物理学教程（上卷）［M］.北京：高等教育出版社，2002.

［2］ 马文蔚.物理学［M］.6版.北京：高等教育出版社，2014.

［3］ 张达宋，李行一.物理学基本教程［M］.3版.北京：高等教育出版社，2008.

THE IMPORTANCE OF EMPHASIZING THE RELATIONSHIP BETWEEN ANGULAR MOMENTUM AND ANGULAR VELOCITY IN A RIGID BODY'S ROTATION ABOUT A FIXED AXIS

Zhou Yuqing
（Department of Physics，Southeast University，Nanjing，Jiangsu 211189）

In college physics textbooks and teaching，little emphasis is put on the relationship between the angular momentum and angular velocity of a rigid body when it rotates about a fixed axis.Instead，attention is focused on the projection of the angular momentum along the axis of rotation.Sometimes，we see equations，such asL=Jω，that are quite misleading.In fact，when a rigid body rotates about a fixed axis，its angular momentum and angular velocity generally point in different directions；there is normally a time-varying external torque acting on it even when it is rotating uniformly.Paper first present a general proof of this assertion and indicate two special situations in whichL andωpoint in the same direction.Then，by using a specific example，paper shows that when a rigid body rotates about a fixed axis，there is generally a changing external torque acting on the axis of rotation in a direction perpendicular to the axis.Finally，paper generalize the conclusion drawn from this particular example，and further illustrate the importance of clarifying the relationship between the directions ofL andω.

rigid body；rotation about a fixed axis；angular momentum；angular velocity；direction；time-varying torque

2015-05-25；

2015-10-25

教育部在线教育研究中心在线教育研究基金（全通教育）重点课题，2016ZD312；江苏省高等教育教学改革项目（省教育厅），2015JSJG118.

周雨青，男，教授，主要从事大学物理教育教学工作，研究方向为凝聚态物理.zhou-yuqing@263.net