基于随机几何理论的毫米波蜂窝系统覆盖研究
李星蓉,李永倩
(华北电力大学 电子与通信工程系,河北 保定 071003)
基于随机几何理论的毫米波蜂窝系统覆盖研究
李星蓉,李永倩
(华北电力大学 电子与通信工程系,河北 保定 071003)
随着移动多媒体业务的日益发展,蜂窝通信的频带日趋紧张,开辟新的频带资源是解决问题的关键技术之一。毫米波频段丰富的频率资源已经成为关注的焦点,它将是下一代蜂窝网络发展的希望所在。提出一种基于随机几何理论的毫米波蜂窝网络基站建模方法,用线段模型对城市中的建筑物进行建模,根据概率理论推导了毫米波蜂窝网络中建筑物的阻挡数量;分析了建筑物阻挡对覆盖产生的影响,研究了毫米波蜂窝网络的覆盖概率与信干比(SignalToInterferenceRatio,SIR)之间的关系,最后通过系统仿真对前面的理论进行了验证,仿真结果与毫米波的传输理论一致。
随机几何理论;毫米波;蜂窝通信;覆盖
过去的十多年,蜂窝通信系统的容量增长了1 000倍。然而,随着用户数量的增加、无线多媒体业务等需求的增大,对下一代(5G)蜂窝通信系统的容量提出了更高的要求。人们希望蜂窝通信系统的容量在后续的10年再增长1 000倍[1,2],如果继续在目前的频谱基础上改进技术已经很难有大的突破,所以就需要寻求新的频谱资源来获得容量的提升。毫米波频段(30~300GHz)有丰富的频谱资源待开发利用,它也就成为了必然的选择方向。据报道,中国发展5G的备选频段为45GHz频段,约有9GHz带宽资源[3],是目前4G系统带宽的200多倍,这就为下一代蜂窝通信系统容量继续提升1 000倍提供了可能。所以,毫米波蜂窝通信有重要的科学研究价值。
近年来,美国、韩国以及欧洲的一些学者已经对毫米波蜂窝通信进行了关注,并陆续报道了一些研究进展。Intel公司的QianLi[3]等人于2014年报道了5G系统可能的频谱划分以及可能涉及到的关键技术。三星公司的WonilRoh[4]等人通过理论分析对毫米波的波束成型技术进行了论证。WooseokNam[5]等人对5G蜂窝网络的干扰管理进行了研究。纽约大学的TheodoreS.Rappaport等人通过理论建模以及对28GHz和73GHz毫米波系统的实际测量,报道了毫米波传输的衰减特性、系统建模方法以及系统容量的评估等[6-7]。德州大学的无线网络及通信小组通过实验测量,对38GHz和60GHz的城市校园环境下的蜂窝通信、角度可控的点对点通信、系统容量等内容进行了报道[8]。而国内文献鲜有对毫米波蜂窝通信研究的报道。本文提出基于随机几何理论的通信链路阻挡建模方法,对毫米波信道上的建筑物等阻挡进行数学建模,并对模型进行理论推导及仿真验证。
1 建模方法
本文选取城市中的建筑物作为建模的研究对象,它们的形状、尺寸、方向都是随机的、独立的,中心点是一个均匀的泊松点过程(PoissonPointProcess,PPP)[9-10]。如果这些建筑物出现在毫米波通信链路上,信号将被阻挡,严重的可能造成通信中断,非常有必要对这些建筑物进行建模分析。可以做如下假设:
假设1,城市中建筑物的形状大多为长方体结构,投影到二维平面上为矩形,设矩形的中心点集合为{Yi},是一个均匀的泊松点过程,密度为λ。
定义矩形集合S⊂R2,矩形的长为Li,宽为Wi,是独立同分布的,则S为一组有界的对象,每个元素s∈S有自己的中心,其方向可以用一个从它的中心起始的矢量来描述,长和宽的概率密度分别为fL(y),fW(y),其方向角用φi表示,在(0,2π]上均匀分布。这样,研究的目标就可以用集合{Yi,Li,Wi,φi}来定义。
假设2,设毫米波蜂窝网络的基站随机分布,则这些基站的中心点位置就是一个均匀的泊松点过程。设基站的集合为Δ={Ti},在R2平面上密度为μ,发射功率为常数P,用户接收机位于原点,从基站到用户的链路用OTi表示,如图1所示。
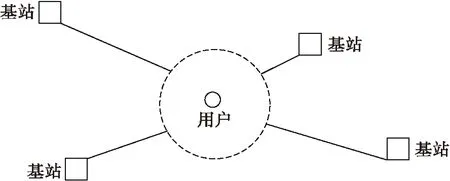
图1 基站及用户所处位置的随机模型
假设3,设位于毫米波通信链路上的建筑物对毫米波信号完全阻挡,即毫米波不能够穿透建筑物,则假设1中的矩形可以简化为一些线段,这些线段的长度和方向是随机变量,每条线段有自己的中心点,这些中心点构成一个泊松点过程。设中心点的集合为φ={Xi},密度为λ;线段的长度为Li,其概率密度函数为fL(x);线段的方向角为θi,θi在(0,2π]均匀分布,如图2所示。
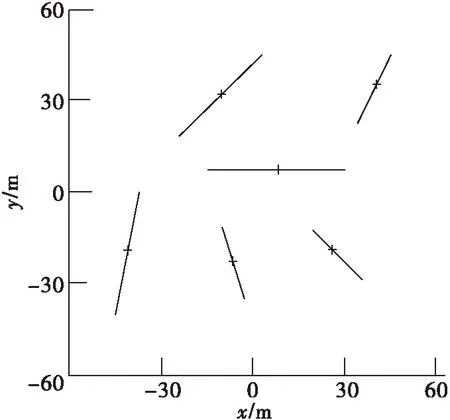
图2 建筑物的线段描述
2 通信链路上建筑物数量M的分布
随机分布的建筑物可以认为是一个随机目标过程,其中心点的集合用{Xi}表示,是一个PPP,这样的研究目标称之为“布尔方案”[9]。建筑物简化后的线段模型可以用一个三元数组(Xi,Li,Θi)来描述。
令线段的集合Φ={Xi∈φ,Li∈(l,l+dl),Θi∈(θ,θ+dθ)},线段的长度为(l,l+dl),方向角为(θ,θ+dθ),这样的一组线段其长度和方向角都是独立的,也是一个PPP,其密度为λl,θ=λfL(l)fΘ(θ)。设基站Ti∈Δ,移动台Ri∈R2,它们之间的距离为d,如图3所示。
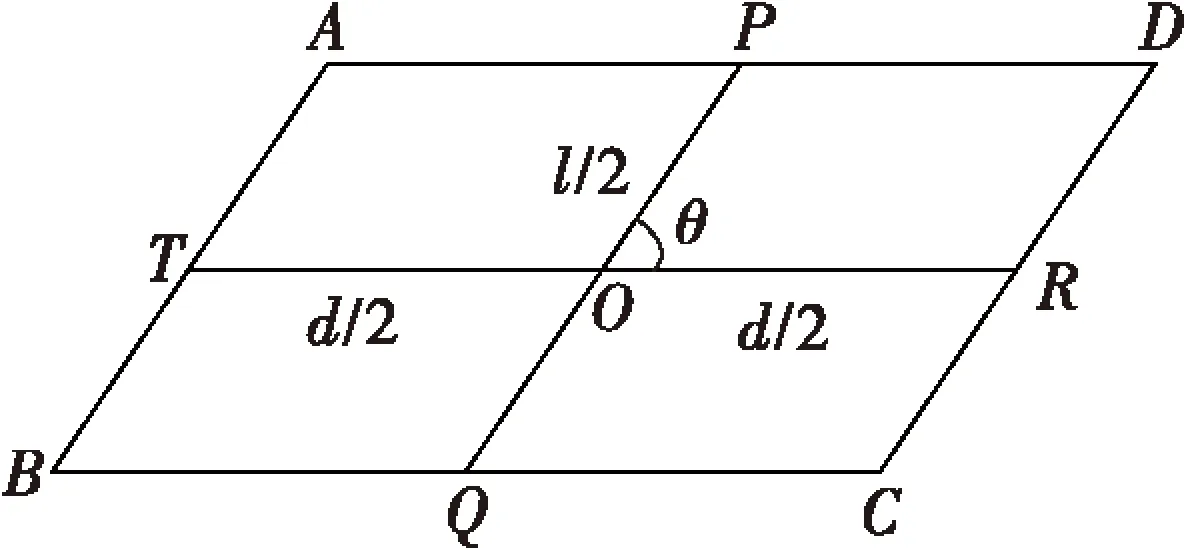
图3 建筑物横穿传输路径模型
如果任意线段PQ(建筑物)属于{(Xi,Li,Θi),Xi∈φ}横穿了传输路径TR,则该线段的中心一定存在于R2平面上的圆A[o,(l+d)/2]中,且同时存在于平面ABCD上[13]。则对毫米波通信链路造成阻挡的概率p=dlsinθ/SA,其中SA为圆A的面积。
设Ml.θ为横穿传输路径TR的线段(建筑物)的数量,由于造成阻挡的建筑物独立均匀的分布于平面ABCD上,则Ml.θ是一个泊松随机变量,其参数为E[Ml.θ]=λl,θldsinθ,对其求积分即可得到横穿传输路径TR的线段(建筑物)的数量。
∫LlfL(l)dl=2λE[L]d/π
(1)
式中:E[L]为建筑物长度的均值。令k=2λE[L]/π,则E[M]=kd。仿真结果如图4所示。
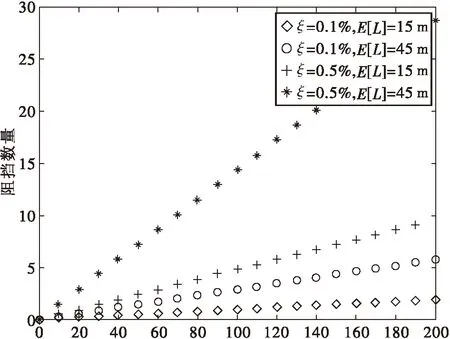
图4 阻挡数量与传输距离及建筑物长度关系图
从图4可以分析,阻挡的数量与建筑物密度、建筑物长度以及基站与用户的距离呈线性关系。随着建筑密度以及建筑物长度的增加,阻挡的数量会逐渐增大。随着基站与用户距离的增加,阻挡的数量会线性增长。
3 建筑物阻挡对覆盖的影响分析
在有不可穿透的阻挡物存在的毫米波蜂窝网络中,用户只能由可视的基站为其提供服务,如果用户所在的可视区域中没有基站存在,该用户将无法接收信号,则称该用户处在“盲区”中。用ξ来表示“盲区”的比率,ξ可用下面的表达式来描述
ξ=1-p
(2)
式中:p为在用户的可视区域至少存在一个基站的概率。
假设用户位于原点,当且仅当所有位于圆B(o,x)内的基站都不能被用户看见时,用户与最近的可视基站的距离大于圆的半径x。设在传输路径上阻挡物的数量是独立的,用户距离最近的可视基站的距离为r,基站的密度为μ,用户与圆外基站连接的概率表示为[11-12]。
P{r>x}=e-2π μT(x)
(3)
其分布函数F(r
对其分布函数求一阶导数,可得其概率密度函数为
fr(x)=2πμxe-(kx+2πμT(x))
(4)
式中:T(x)=2[1-e-kx(1+kx)]/k2。
对式(3)仿真可得与圆外基站连接的概率曲线,如图5所示。
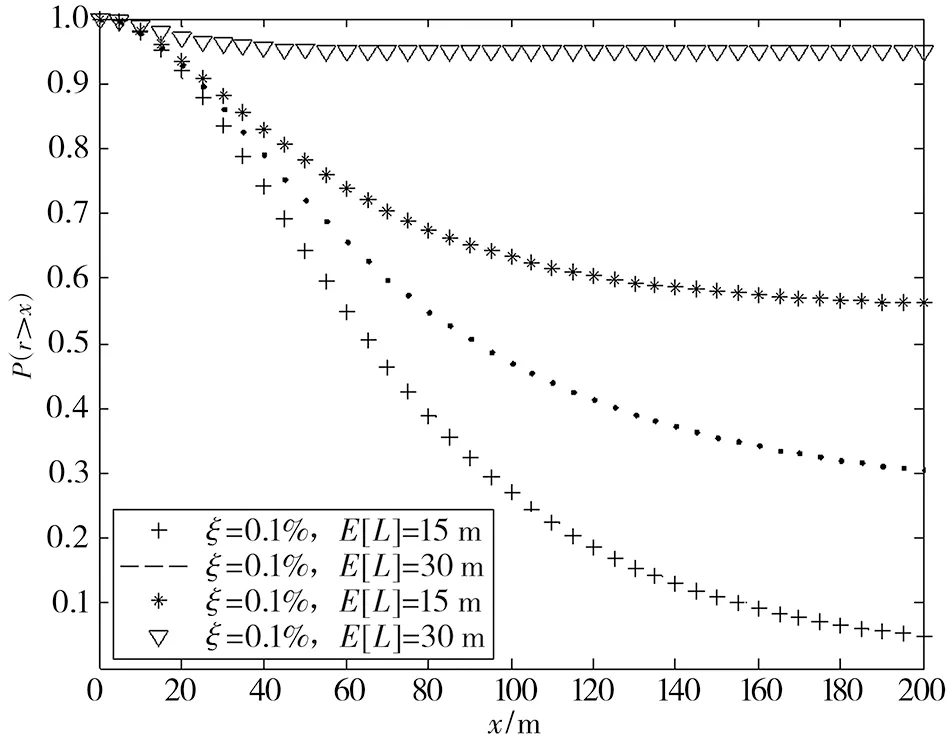
图5 与圆外基站连接的的概率分布曲线
对图5的仿真曲线分析可得:1)随着圆B(o,x)半径的增加,圆B(o,x)内的基站数量将会增多,位于原点的用户与圆内基站可视的概率加大,而与圆外的基站连接的概率降低。2)随着圆内建筑物密度的增加以及建筑物长度的变大,会显著降低位于原点的用户与圆内基站可视连接的概率,这就迫使用户去寻找与圆外的可视基站连接。这种情况下,用户距离最近的可视基站的距离r>x的概率将会变大。
“盲区”在整个网络区域中所占的比率如
(5)
令建筑物密度与基站密度的比值为ρ=λ/μ,把k=2λE[L]/π代入式(5)化简得
(6)
为了考查建筑物密度、基站密度、建筑物长度对可视连接的影响,对不同取值ρ以及E[L]情况下存在“盲区”的概率进行了计算,得到仿真曲线如图6所示。
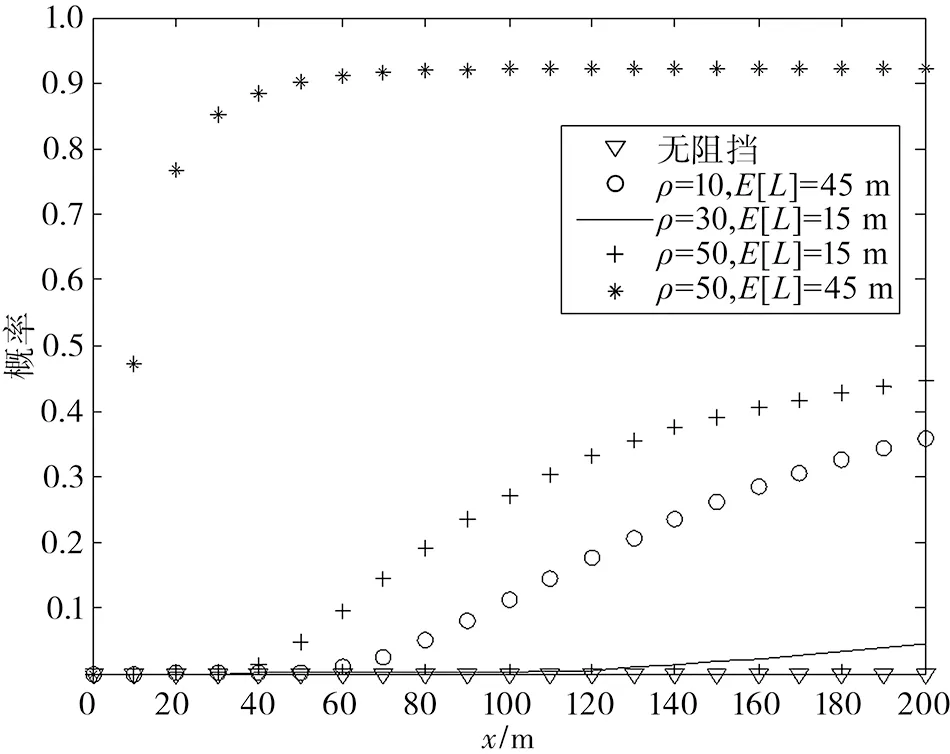
图6 “盲区”概率与不同的ρ以及E[L]的关系曲线
从图6可以得出几个结论:1)“盲区”概率与几个变量之间并不是简单的线性关系,在无阻挡的环境下,位于原点的用户始终与圆内最近的基站进行连接,而不会去寻找较远的基站,不存在“盲区”;2)随着建筑物密度增大以及建筑物尺寸的增加,“盲区”存在的概率变大;3)建筑物尺寸的增加对可视连接的影响比建筑物密度的增加更明显,当建筑物长度为45m,ρ=50时,可以发现即使用户距离基站很近,也有可能处于“盲区”,系统已经无法使用,这与毫米波穿透能力差、容易被阻挡的理论一致。
4 信干比对覆盖的影响分析

(7)式中:h为基站到移动用户的增益;d为移动用户到可视基站的距离;α为路径损耗指数,一般在1.5~6.0[11]。式中的第一项为移动用户正确接收到的目标基站发来的信号,第二项为其他非目标基站发来的信号在用户位置的叠加,会对本移动用户接收信号造成干扰,n为加性高斯白噪声,均值为0,方差为σ2,则信号功率与噪声功率加干扰功率的比率为
(8)
在蜂窝无线网络中,相比于小区间干扰,热噪声产生的影响很小,即可假设σ2→0。则式(8)可简化为
(9)
考虑到用户只跟距离自己最近的可视基站连接,则式(9)可变为
(10)
覆盖概率可以定义如下
Pc(T)=P{SIR>T}
(11)
式中:T为SIR阈值。这个表达式可以理解为:所有用户信干比的平均值在任意时刻都能达到T,或者网络中在任意时刻SIR都能达到T的面积所占整个网络面积的百分比。则覆盖概率的表达式可表示为
(12)
式中:fr(x)为概率密度函数。通过系统仿真,所得覆盖概率与SIR阈值T、建筑物尺寸以及建筑物密度之间的关系曲线如图7所示。
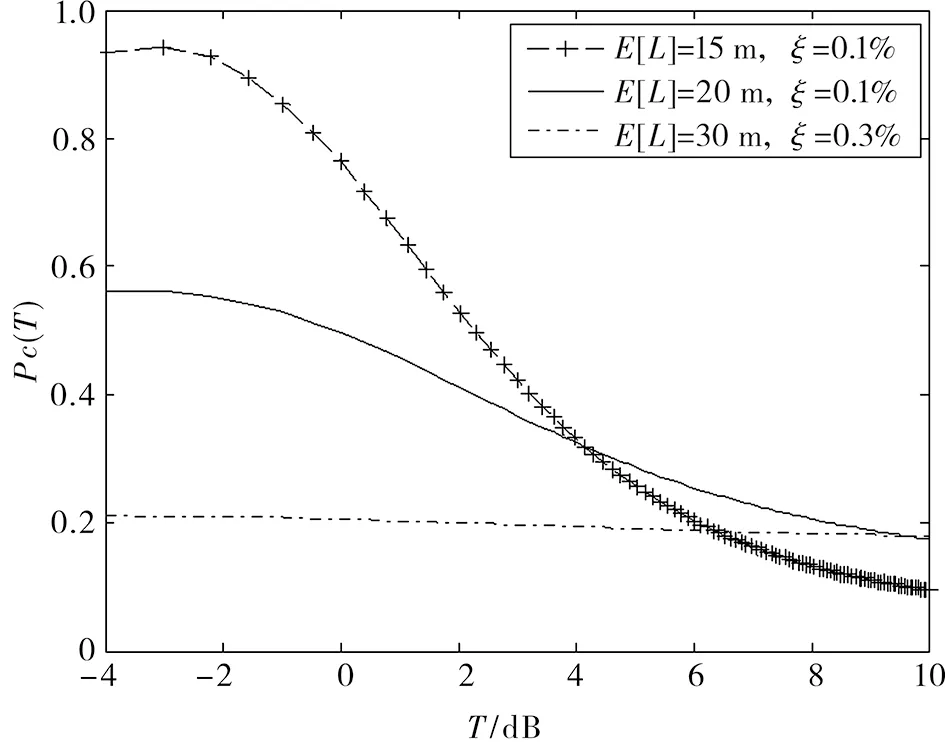
图7 覆盖概率与SIR门限的关系曲线
仿真中,选取路径衰落指数α=4,基站的布置按照半径为100m的圆面积上放置一个基站,可以求得基站的密度μ=3.85×10-5,从图7可知:1)在建筑物的尺寸较小,设定SIR阈值T较低的情况下,覆盖概率非常好,达到95%以上;2)建筑物的尺寸以及建筑物的密度对覆盖概率有显著影响。随着建筑物尺寸的变大,覆盖概率快速变小,如图7中,当建筑物尺寸E[L]从15m变大到20m,在建筑物密度不变的条件下,覆盖概率从95%以上快速下降到不足60%,当E[L]=30m,建筑物密度增大到0.3%时,覆盖概率一直都很低。这与毫米波容易被阻挡的传播特性一致。在实际应用中,必须通过增加基站的数量,或者与其他频率的蜂窝通信系统协调工作等方法来克服阻挡产生的影响。这部分工作将在后续的研究中开展。对于E[L]=15m和E[L]=20m两条曲线随着阈值T的变大出现了交叉,这是因为建筑物不仅阻挡了有用信号,同时对周围基站发来的干扰信号也起到了阻挡作用,以至于在性能较差的信道上,尺寸大的建筑物造成的信干比的恶化要缓慢一些。
5 结论
毫米波频段有丰富的频带资源,为下一代无线通信系统的发展提供了带宽的保证,因而毫米波蜂窝通信技术的研究引起了广泛关注。本文提出了一种基于随机几何理论对毫米波蜂窝网络的基站进行泊松点建模的方法,深入讨论了建模的基本理论,根据毫米波穿透性差的特点,用线段方法对矩形建筑物进行了简化处理,用概率方法对传播路径上的建筑物阻挡数量进行了量化计算,推导了建筑物的密度、尺寸对蜂窝网络覆盖的影响,并对推导结果进行了系统仿真。仿真结果与毫米波的传播特性一致。
[1]FETTWEISG,ALAMOUTIS. 5G:personalmobileinternetbeyondwhatcellulardidtotelephony[J].IEEEcommunicationmagazine, 2014(2):140-145.
[2]GULTEKINM,KESOGLUH,MENDERESC,etal. 5Gwirelesscommunicationsystems:prospectsandchallenges[J].IEEEcommunicationmagazine,2014(2):62-64.
[3]LIQ,NIUH,WUG.5Gnetwokcapacitykeyelementandtechnologies[J].IEEEvehiculartechnologymagzine,2014(3):71-78.
[4]ROHW,SEOLJY,PARKJH.Millimeter-wavebeamfomingasanenablingtechnologyfor5Gcellularcommunications:theoecticalfeasibilityandprototyperesults[J].IEEEcommunicationmagazine,2014(2):106-112.
[5]WOOSEOKN,DONGWOONB,JUNGWONL,etal.Advancedinterferencemanagementfor5Gcellularnetworks[J].IEEEcommunicationsmagazine,2014(5):52-60.
[6]NIES,SUNS. 28GHzand73GHzsignaloutagestudyformillimeterwavecellularandbackhaulcommunications[C]//Proc.IEEEICCWirelessCommunicationsSymposium.[S.l.]:IEEE,2014:4856-4861.
[7]LIUY,SUNS.Millimeterwavechannelmodelingandcellularcapacityevaluation[J].IEEEjournalonselectedareasincommunications,2014,32(6):1164-1178.
[8]BEN-DORE,QIAOY. 38GHzand60GHzAngle-dependentPropagationforCellular&Peer-to-PeerWirelessCommunications[C]//Proc.IEEEICCWirelessCommunicationsSymposium. [S.l.]:IEEE,2012:4568-4573.
[9] 史习智,龚光鲁,徐明译. 泊松点过程[M].北京:科学出版社,2013.
[10]GIORGETTIA,CHIANIM.Astochasticgeometryapproachtocoexistenceinheterogeneouswirelessnetworks[J].IEEEjournalonselectedareasincommunications,2009,27(7):1268-1281.
[11]BAITY,VAZER.Analysisofblockageeffectsonurbancellularnetworks[J].IEEEtransactionsonwirelesscommunications,2014,13(9):5070-5083.
[12]ANDREWSJG,BACCELLIF,GANTIRK.Atractableapproachtocoverageandrateincellularnetworks[J].IEEEtransactionsoncommunications,2011,59(11):3122-3134.
[13]STOYAND,KENDALLW,MECKEJ.Stochasticgemoetryanditsapplications[M]. [S.l.]:JohnWileyandSons,1995.
李星蓉(1975— ),博士生,讲师,研究方向为无线通信;
李永倩(1958— ),博士生导师,主要研究方向为光通信与光传感、无线通信等。
责任编辑:许盈
Coverageresearchofmillimeterwavecellularsystembasedonstochasticgeometrytheory
LIXingrong,LIYongqian
(Department of Electronics and Communication Engineering,North China Electric Power University,Hebei Baoding 071003,China)
Thefrequencybandofthecellularcommunicationbecomesveryscarce,findingnewfrequencyresourcesisoneofthekeytechnologiestosolvethisproblem.Millimeterwavebandhasbeenwidelyconcernedforitsabundantfrequencyresource,anditwillbeapromisingtechnologyforthefifthgenerationcellularsystem.Inthispaper,amillimeterwavecellularnetworkbasestationmodelingmethodbasedonstochasticgeometrytheoryisproposed,theblockageofbuidingstomillimeterwavecellularnetworkisdeduced,therelationshipbetweencoverageprobabilityandSIRisstudied.Atlast,thetheorymentionedbeforeisverifiedthroughsystemsimulation,andthesimulationresultisagreementwiththetheoryofmillimeterwavetransmission.
stochasticgeometrytheory;millimeterwave;cellularcommunication;coverage
TN915
ADOI:10.16280/j.videoe.2016.08.011
中央高校基本科研业务费专项(2015MS101);国家自然科学基金项目(61302106);河北省自然科学基金项目(F2014502098)
2016-01-19
文献引用格式:李星蓉,李永倩.基于随机几何理论的毫米波蜂窝系统覆盖研究[J].电视技术,2016,40(8):57-61.
LIXR,LIYQ.Coverageresearchofmillimeterwavecellularsystembasedonstochasticgeometrytheory[J].Videoengineering,2016,40(8):57-61.

