基于小波变换的桥梁动态称重系统车轴高精度识别研究*

赵　华，谭承君，张龙威，乔东钦

(湖南大学 土木工程学院 风工程与桥梁工程湖南省重点实验室，湖南 长沙　410082)



基于小波变换的桥梁动态称重系统车轴高精度识别研究*

赵华†，谭承君，张龙威，乔东钦

(湖南大学 土木工程学院 风工程与桥梁工程湖南省重点实验室，湖南 长沙410082)

首先利用小波变换对一不能明显识别车轴信息的数值仿真信号进行处理，证明小波变换能够高效放大车轴经过传感器时产生的不连续变化斜率，从而识别出车轴信息.然后基于实桥测试，对那些不能直接识别出车辆信息的FAD信号，通过联合控制最小Shannon熵值和最大相关系数选取最适变换尺度和最适变换小波函数进行小波变换.分析结果表明：对于不能直接识别出车辆信息的FAD信号，小波变换也能准确地识别车辆行驶速度、车轴数目以及车轴间距.小波变换可提高桥梁动态称重(BWIM)系统车轴识别的效率及精度，为将BWIM系统发展为超载车辆控制的有效工具提供技术支撑.

桥梁动态称重；车轴识别；小波变换；小波函数选取；变换尺度

我国超载现象比比皆是，超载车辆对道路和桥梁造成的破坏不容忽视[1].近些年来，超载车辆导致桥梁垮塌的报道屡见不鲜.高效率、高精度的超载车辆监管系统可控制超载车辆并监测桥梁安全，在我国有着广阔的应用前景.

动态称重系统(weigh-in-motion：WIM)近年来在国际上越来越多地应用于对桥梁和道路交通车辆的监测.该技术在测试车辆数据时不需要中断交通，效率较高，是一种获取车辆荷载数据、控制超重车辆的有效工具.传统的动态称重系统(也称为路面动态称重系统：Pavement WIM)通过在路面埋置传感器来测试通行车辆的轴重、轴距和车速等信息.该系统是永久性的，不能拆迁，使用寿命较短，且安装及维护费用较高，精度也有待提高[2-5].桥梁动态称重系统(bridge weigh-in-motion：BWIM)直接利用桥梁为载体，在线监测桥梁在移动车辆荷载作用下的动态响应，并通过程序反算出车辆轴重.和传统路面WIM系统相比，BWIM系统不仅可以在不阻断交通的情况下连续不间断地识别车辆轴重和总重，而且可以在线监测桥梁在车辆荷载作用下的动态响应信号，进而获得结构的实际影响线以及在车辆荷载作用下的结构荷载横向分布参数和桥梁冲击系数等[4,6].

BWIM的概念最初由Moses[7]于1979年提出.BWIM系统利用安装在主梁下缘的传感器所采集的动态信号反算出车辆轴重.早期BWIM系统除了在主梁下缘安装传感器外，还需要在桥头路面上埋置便携式磁带开关或压电电缆来测试车辆速度、轴数、轴间距等信息，所以早期BWIM系统也存在耐久性问题，且安装时需要中断交通，更换也不易[6,8-10].

近几十年来，各国学者在原始BWIM模型基础上推广和改进，共同创建了新型商业BWIM系统[6,9-11].

新型BWIM系统摒弃了早期BWIM系统所需的埋置在桥头路面上的便携式磁带开关或压电电缆，而是直接在桥面板下安装额外的传感器(也称车轴探测传感器或FAD传感器)，从而获得车轴信息. 新型BWIM系统的安装、调试及数据采集全部在桥下进行，桥面上不布置任何测试设备.相较于早期BWIM系统，新型BWIM系统不仅可以在不阻断交通的情况下连续不间断地识别车辆轴重和总重，更具有携带方便、安装和测试隐蔽、可以反复使用，且安装、维护及使用成本低等优点[4].

Moses[7]，Znidaric[11]和Peters[12]都曾提到车辆信息识别(轴数及轴间距)的准确度是影响BWIM系统轴重及总重识别精度的一个主要因素，同时有效且准确地识别出车轴信息也是BWIM系统精确识别车辆轴重的前提及基础.然而试验证明，有时难以直接从FAD信号中准确识别车辆信息，特别是在连轴(相邻车轴间距很小)或信号动态成分较大的情况下[8,13-14].Dunne[8]和Chatterjee[13]提出通过对FAD信号进行小波变换可更有效地识别车辆信息，但对于小波函数选取及最适变换尺度都缺少研究.

本文基于仿真分析及实桥测试结果(湖南省怀化市舞水五桥引桥的现场测试)，在标定车辆经过测试桥梁时，采集记录FAD信号和桥梁桥底动态响应信号，结合最小Shannon熵值以及最大相关性从而选取合适小波函数以及变换尺度，并利用小波技术变换FAD信号来获得未能直接识别的车辆信息.分析结果表明：作为强大的信号处理工具，小波变换在BWIM系统中能够有效提高对车轴信息的识别.

1　小波理论

1982年法国工程师Jean Morlet 首先提出小波变换的概念[15]，它可以认为是经典傅里叶变换的延伸.两者最大的区别在于小波变换可以同时在时域和频域上定域，而傅里叶变换只是时域和频域之间的转换工具.小波变换可分为连续小波变换(Continuous wavelet transform：CWT)和离散小波变换(Discrete wavelet transform：DWT).

1.1连续小波变换

连续小波变换的数学定义为：

(1)

小波一词意味着特定的小波函数，即式(1)中的ψ(t)，例如db2和rbio2.4(图1)等.这种小波函数都是紧支的，即函数的定义域是有限的.傅里叶变换是将信号分解成一系列不同频率的正弦波叠加，而小波变换是通过缩放和平移这些小波函数来逼近信号.显然对于一些尖锐变化的信号，用不规则的小波函数逼近要比光滑的正弦曲线好.

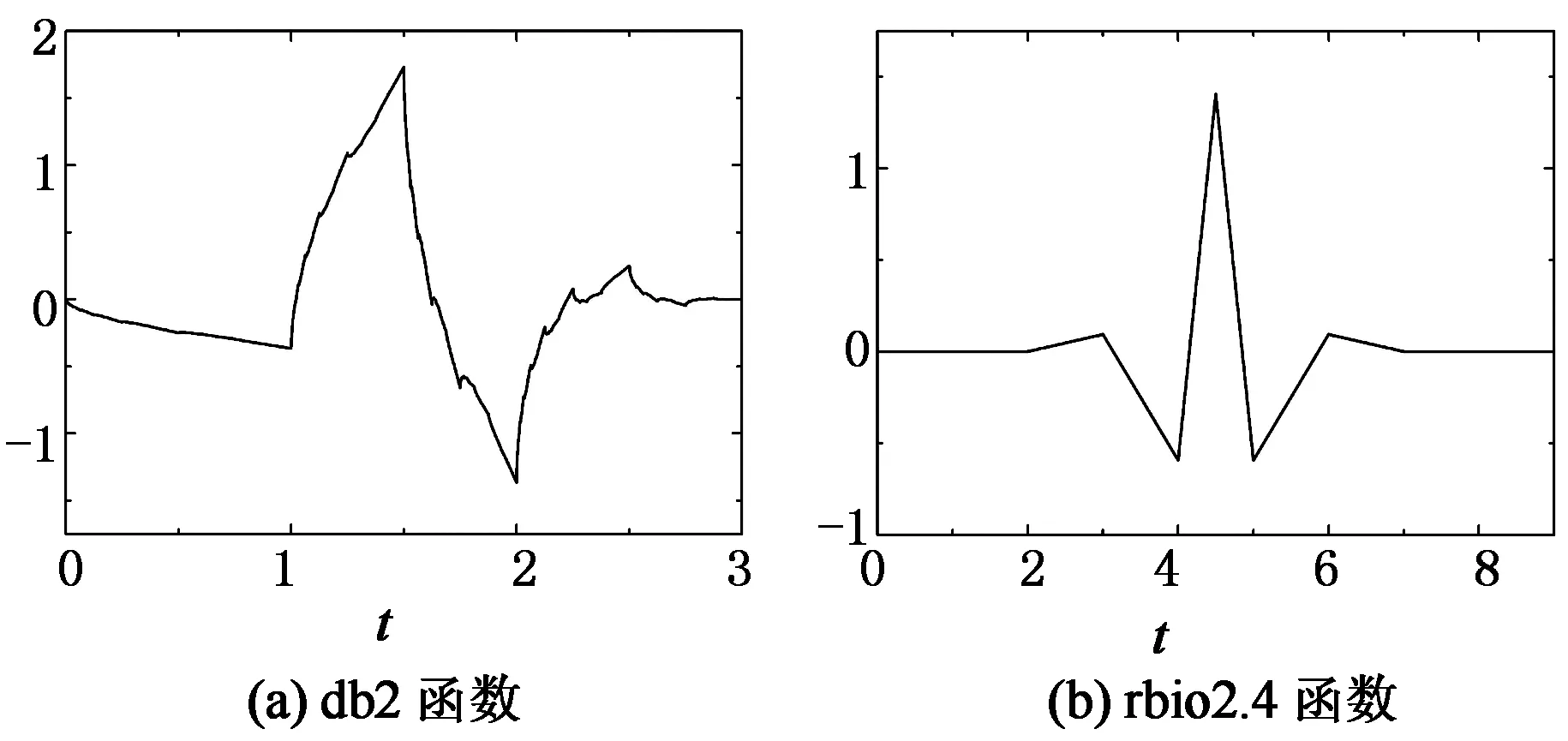
图1　小波函数Fig.1　Wavelet functions

经过连续小波变换得到许多小波系数，这些系数就是缩放因子(尺度)和平移(位置)的函数，其中小波分解尺度与傅里叶变换中的频率相对应，所以连续小波变换又可以定义为式(2).它表示信号f(x)与被缩放和平移的小波函数ψ(t)之积在信号存在的整个时间段求和的结果.

(2)

1.2最适小波函数和变换尺度的选取

在MATLAB小波分析工具中有13个小波函数族，包括60多个常用小波函数，而对于同一个目标信号，每一个小波函数通过变换都会得到不一样的结果.小波变换最大的挑战是对于不同情况怎么选取小波函数来获得最理想的结果.目前，对于小波函数选取的方法总体可以分为两类：定性方法和定量方法.

定性方法是基于小波函数的本身基本特性(正交性、对称性、紧支性、光滑性、消失矩)或通过目标信号与小波函数之间的形状匹配度来选取最适小波函数.对于特定的目标信号，需要针对想要结果的特性选取合适的小波函数.例如，考虑到小波函数的紧支性、消失矩和正交性，选择Coif4小波函数以便有效分离肌动电流图中的脉冲波和滋补成分[16].

定性方法中大部分是通过肉眼来判断，缺少客观依据，而定量方法则是通过计算出特定的数值(能量、熵值、相关系数等)以便更客观地对比小波函数之间的差异[17].

对于连续小波变换，它在每个可能的尺度上都进行计算，得到一系列的小波变换系数，其中只有部分结果是有用的，所以如何选取变换尺度至关重要.本文提出采用最小Shannon熵方法选择最佳小波变换尺度[17].

小波变换系数在尺度s下的能量为：

(3)

式中：wt(s,i)为小波变换系数；N为小波变换系数总容量.

小波变换系数的Shannon熵的分布如下：

(4)

显然小波变换系数Shannon熵值的范围为0≤Eentropy(s)≤log2N.仅当所有小波变换系数都为0时，Shannon熵值为0；且仅当所有小波变换系数均相同时，Shannon熵值等于log2N.Shannon 熵值的大小反映了小波变换系数概率分布的均匀性，熵值越大，概率分布越不均匀，能量就越分散；熵值越小，概率分布越均匀，能量分布就越集中[17].因此，对于不同尺度下一系列的小波变换系数，其中某尺度对应的小波变换系数包含少量大幅度的系数且其他的小波系数相对而言较小或者可以忽略时，将产生最小的Shannon熵值[17].这一特性正适合在BWIM系统中利用FAD信号对车轴信息进行识别.因为对于FAD信号，只需考虑当车轴经过FAD传感器时产生的明显波峰，其他时刻的振荡均需忽略，使得车轴产生的峰值更加凸显(即能量集中分布在车轴经过传感器时刻).

2　数值仿真结果的小波变换

仿真分析中模拟一辆两轴车以20 m/s的速度经过跨度为15 m的简支梁.车辆模型的简化车身质量平均作用在车轴上(如图2所示),且每个车轮自身重为7.5 kN.表1列出了计算分析中车辆和桥梁采用的详细参数.

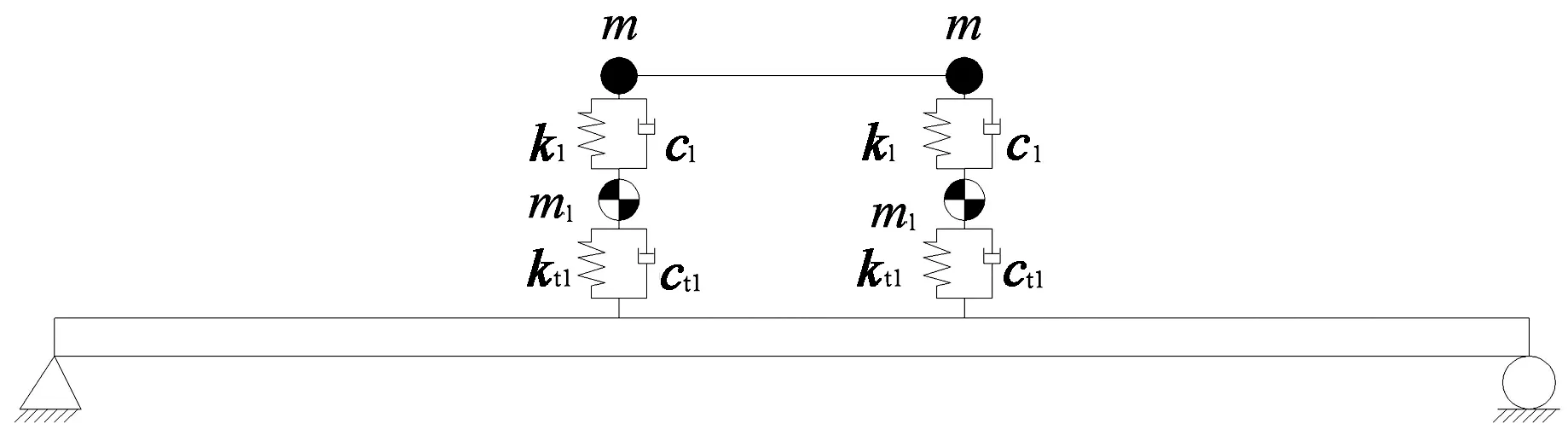
图2　车桥模型Fig.2　Vehicle and bridge model

图3示出了车辆经过桥梁时数值模拟产生的跨中梁底动态应变响应信号(采样频率为6 400 Hz).由于车桥耦合振动，很难直接从图中获得车轴经过桥梁跨中时刻的准确时间信息.本文拟用rbio2.4小波函数对图3中模拟信号进行连续小波变换，并为了选取最适合变换尺度，算出利用rbio2.4函数的连续小波变换在尺度1至64的Shannon熵值(图4).显然，当尺度为1时，Shannon熵值最小，所以选取当尺度为1时的连续小波变换系数作为变换结果(图5).其结果显示的2个明显峰值，表明所经过车辆为一两轴车.2个峰值所对应的时刻分别为0.375 s和0.450 s，因此2个车轴经过跨中点的时间差即为0.075 s.已知车辆行驶速度为20 m/s，即可算得峰值间距离(即轴距)为1.5 m，与车轴间距模型的设计值完全吻合.由此表明经过小波变换后得到的波峰对应时间点即为车轴经过跨中点的瞬间.

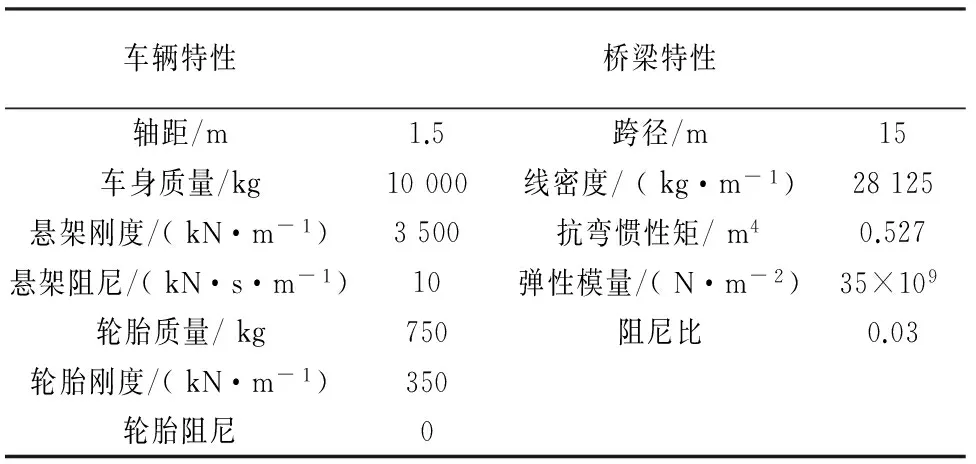
表1　车桥模型参数

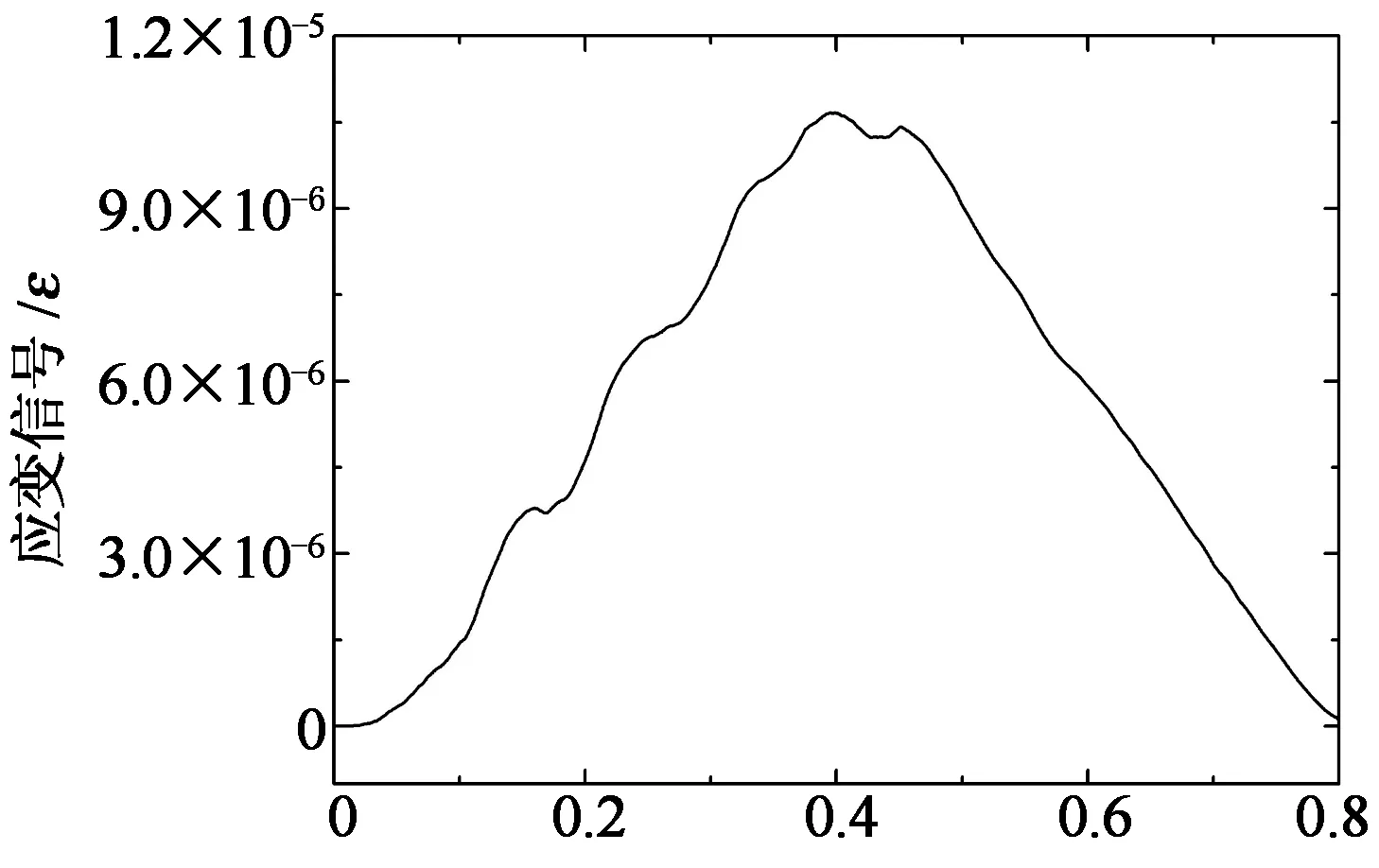
t/s图3　跨中梁底动态应变响应信号Fig.3　Signals of dynamic strain response at mid-span

尺度图4　模拟信号的熵值曲线Fig.4　Curve of Shannon entropy from simulation signal

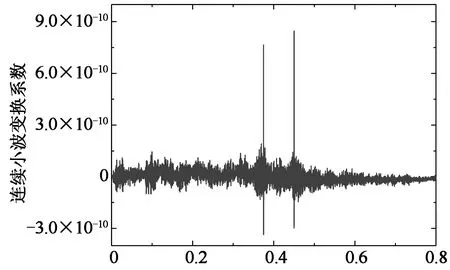
t/s图5　模拟信号小波变换结果Fig.5　The outcomes after wavelet transform for simulation signal

以上分析表明：对于没有出现任何尖峰的跨中梁底车桥耦合振动信号，小波变换能非常有效地从这些信号中识别出各车轴经过传感器的准确时间信息.其原因在于：这个数值模拟信号是由具有非常“尖角”的静态信号叠加在振动效果上所得到的.而小波变换就像是信号的放大器，能够找到并放大这些“尖角”.

3　实桥测试

3.1试验桥跨简介

实桥测试选择湖南省怀化市舞水五桥怀黔路侧简支跨引桥作为测试跨.该桥主桥为预应力混凝土连续箱梁桥，主桥跨径布置为65 m+100 m+65 m.主桥两侧各有一跨径为40 m引桥，为全预应力混凝土简支T梁结构，其横向由10片T梁组成.测试跨的传感器布置如图6, 图7和图8所示.40 m引桥沿行车方向共布置5道横隔板，如图8所示.该桥横向宽度为24.0 m，桥宽布置为：2.0 m(人行道)+3.0 m(非机动车道)+4×3.5 m(行车道)+3.0 m(非机动车道)+2.0 m(人行道)，具体布置如图7所示.

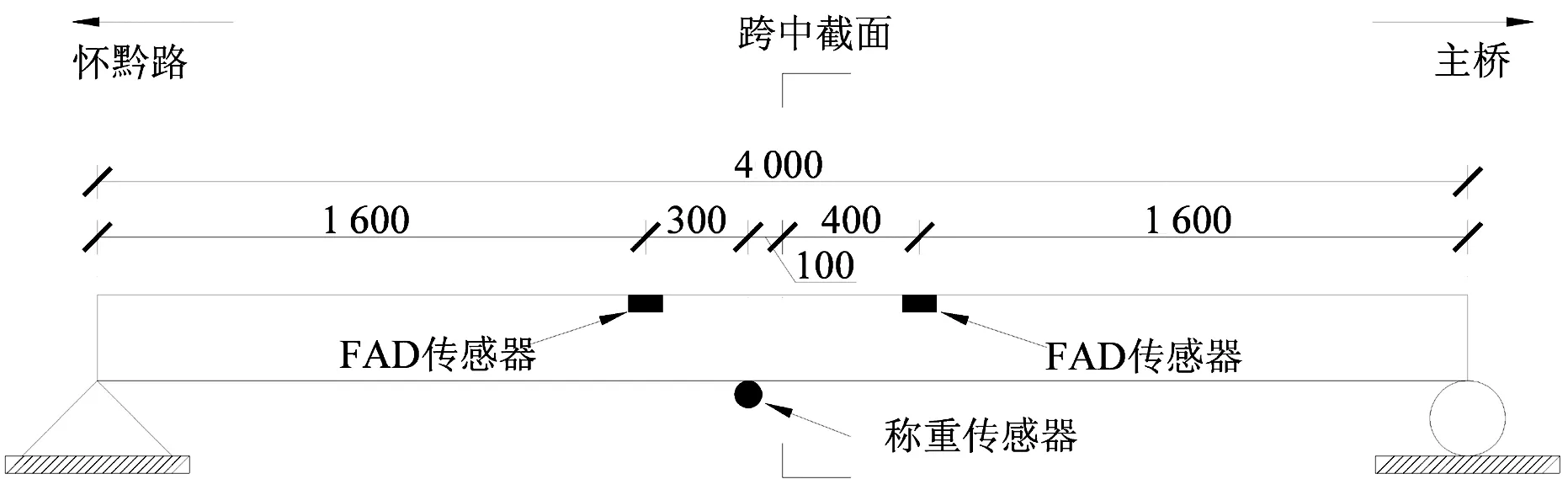
图6　测试桥跨及传感器立面布置示意图(单位：cm)Fig.6　Elevation layout of test-span and sensors

由图6，图7和图8可以看到，在每个车道对应的桥面板下都安装了一对FAD传感器，在每片T梁下缘都安装了一个采集桥梁动态应变的传感器(称重传感器).如图8所示，编号1—10为布置在梁底的称重传感器，编号11—18分别为布置在各个车道桥面板下的FAD传感器.其中编号为11和15的传感器对应于行车道1，编号分别为L1-FAD1和L1-FAD2； 编号为12和16的传感器对应于行车道2，编号分别为L2-FAD1和L2-FAD2；编号为13和17的传感器对应于行车道3，编号分别为L3-FAD1和L3-FAD2；编号为14和18的传感器对应于行车道4，编号分别为L4-FAD1和L4-FAD2.对各车道而言，FAD1 和FAD2分别表示车辆先经过编号为FAD1的传感器，然后再经过编号为FAD2的传感器.

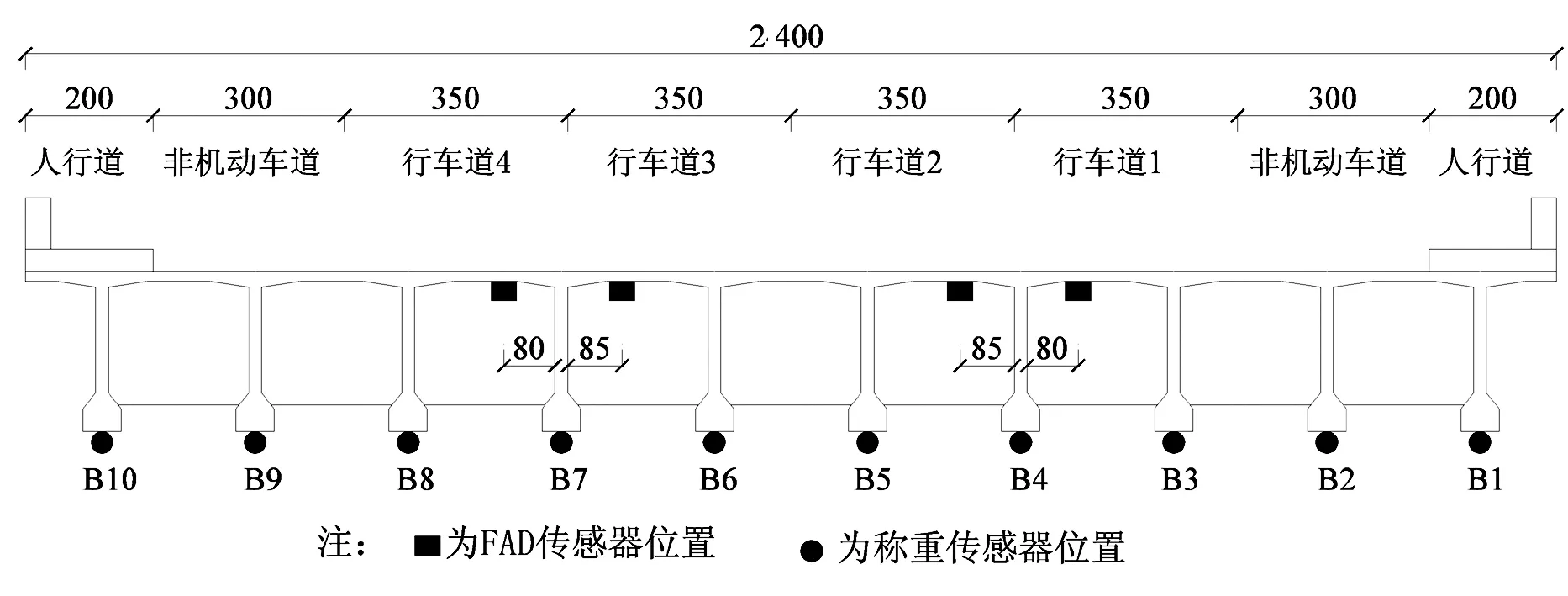
图7　测试桥跨及传感器横断面布置示意图(单位：cm)Fig.7　Cross-sectional layout of test-span and sensors

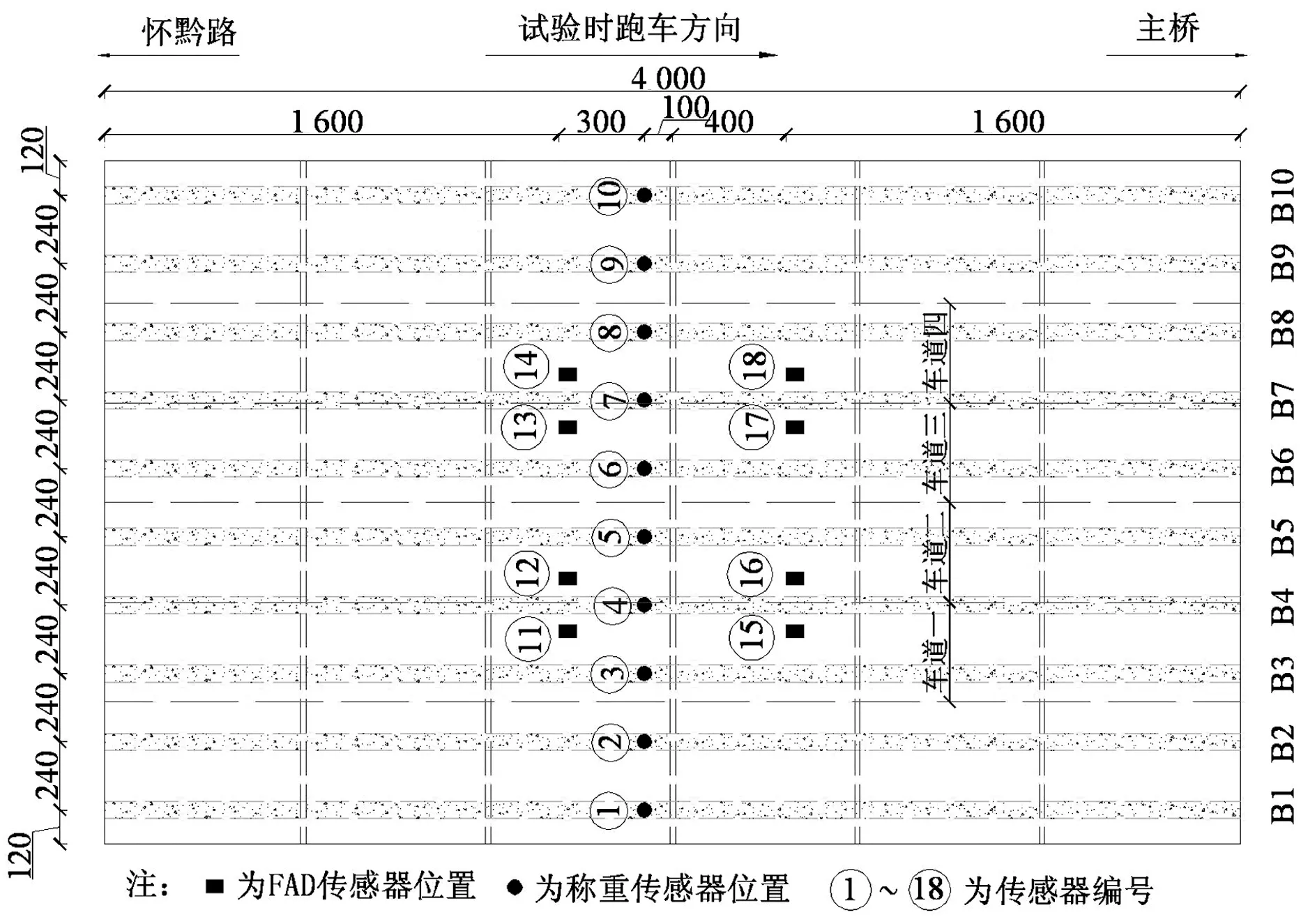
图8　传感器平面布置示意图(单位：cm)Fig.8　Plane layout of sensors

在新型BWIM系统中，对测试的桥跨结构，要事先用标定车对该桥跨进行标定试验.在整个标定试验中采用标定车(已知轴重和轴距)重复进行跑车试验，然后根据测试得到的动态响应来修正或计算结构的实际影响线.在标定后得到的影响线基础上，以FAD传感器识别的车辆信息(轴数、轴距等)为前提，根据连续采集的梁底动态应变计算出行驶车辆轴重及总重[4,6,9].

试验现场传感器的布置图如图9所示.试验时选取2辆两轴车(分别称为A和B)作为标定车，同时或分别在每个车道上重复进行跑车试验(如图10所示).试验中所采用的标定车详细信息见表2.试验过程中采用扬州科动公司生产的KD4001工具式应变传感器作为测试元件，日本TML公司生产的动态应变仪DC-204R作为数据采集仪.标定试验采集频率为200 Hz.

合作社按照“利益共享、风险共担”的股权分红模式。2015年7月至2018年4月合作社财务数据为：总收入865.88万元，其中竹材638.7万元、毛料153万元、冬笋33.4万元、山林租金9.3万元、政府补贴31.48万元；总支出426.92万元，其中务工支出414.1万元(用于劈山及竹材采伐)、管理支出12.82万元；总利润438.96万元，其中2016—2017年合作社2次分红共计257.36万元、提取公积金13万元，2018年已收益168.6万元。在对社员的访谈中得知，合作社统一经营后，分红收入要高于自己经营收入。

图9　传感器现场布置图Fig.9　Setup of the installed sensors

图10　标定车A和BFig.10　Calibration trucks A and B表2　标定车信息Tab.2　Information of calibration vehicles

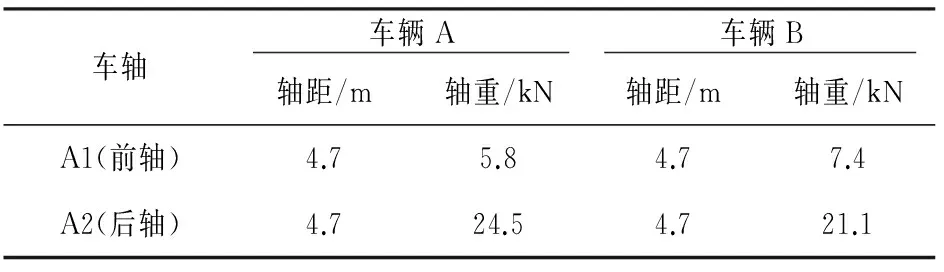
车轴 车辆A 车辆B 轴距/m轴重/kN轴距/m轴重/kNA1(前轴)4.75.84.77.4A2(后轴)4.724.54.721.1

3.2试验结果的小波变换

3.2.1单辆车过桥时FAD信号的小波变换

在试验中，当标定车辆行驶过桥时，采集的FAD信号大部分能够直接识别车辆信息，但有时由于车桥耦合振动的动态成分较大而导致FAD信号难以直接识别车辆信息.例如仅车辆A在车道3跑车时，如图8所示，编号为13的传感器(L3-FAD1)和编号为17的传感器(L3-FAD2)记录了桥面板下缘处在车辆荷载作用下的动态应变信号(图11).从图中可清晰地看出，标定车经过车道3时，先经过L3-FAD1，然后再经过L3-FAD2，这和传感器的布置一致.

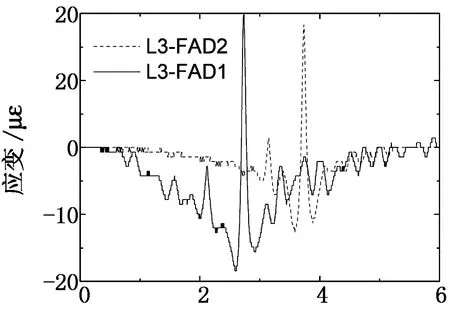
t/s图11　第三车道FAD信号Fig.11　FAD signals from lane 3

如图11所示，L3-FAD1和L3-FAD2的信号都只出现了一个明显的峰值.当标定车A的2个轴分别经过每一个FAD传感器时，该传感器采集的测试信号理应会显示出2个明显的峰值，但是L3-FAD2的信号只显示了一个明显峰值信号以及在它之前的一个小波峰，而L3-FAD1的信号只呈现了一个明显峰值信号及它前后许多小波峰.就L3-FAD1信号而言，程序难以直接识别出哪些波峰是由于车轴经过该FAD传感器时所产生的.

小波变换拟用来提高FAD信号的车轴信息识别.为了更好地说明小波函数以及变换尺度的选取，以ReverseBior(rbio)小波函数族中rbio1．3, rbio2.2, rbio2.4, rbio2.8, rbio3.3, rbio3.9, rbio4.4和rbio6．8为例.对于L3-FAD1信号，由公式(3)和(4)算出上述小波函数从尺度1至64的连续小波变换的Shannon熵值分布(图12).由图可知，每个小波函数所对应小波系数的Shannon熵值曲线在尺度5至15存在最小值.以rbio2.2函数为例，当尺度为6时，Shannon熵达到最小值.图13列出了rbio2.2在不同尺度下的连续小波变换系数.可以看出，当尺度较小时，小波变换系数杂乱无序，对车轴信息识别毫无意义；当尺度较大时，小波变换系数的波峰将被稀释(包括车轴产生的波峰)，这也导致无法精确识别车轴信息.当Shannon熵值最小时(尺度为6)呈现出2个明显能识别的波峰，在此能量集中分布于2个波峰所对应的时刻.并且当尺度与最小Shannon熵值对应的尺度越接近时，由车轴经过FAD传感器产生的波峰越明显.因此，也证明使Shannon熵值最小的小波变换尺度对应的小波系数能获得最佳车轴识别效果.

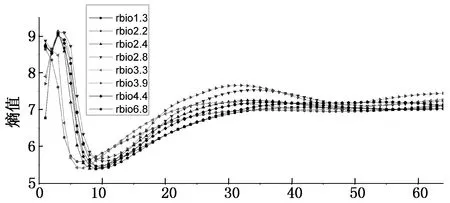
尺度图12　Shannon 熵值分布Fig.12　Distribution of Shannon entropy

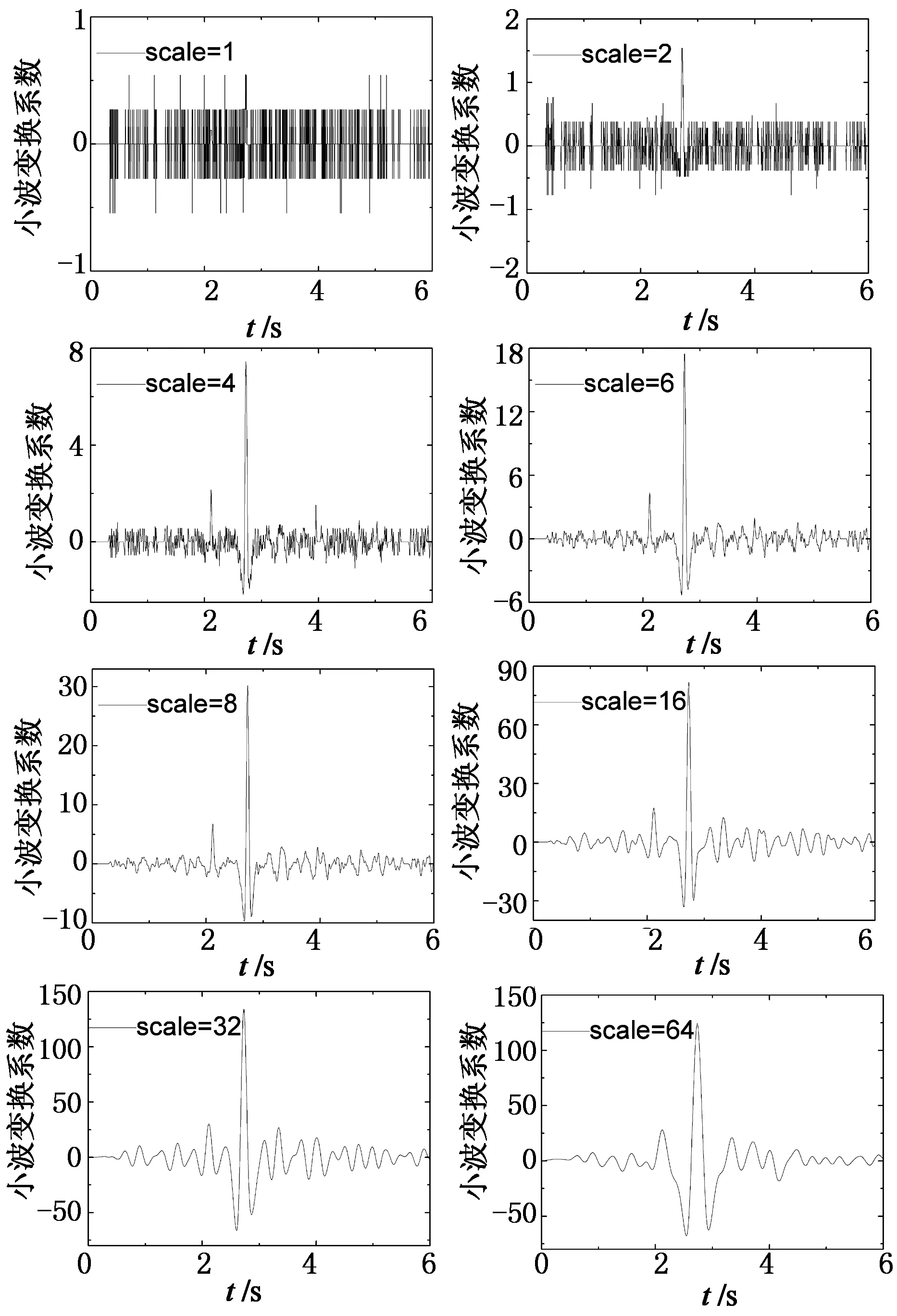
图13　Rbio2.2不同尺度下连续小波变换结果Fig.13　CWT outcomes at different scales from rbio2.2

前述已证明在最小Shannon熵时，能够得到最佳车轴信息识别效果，图14列出上述一系列小波函数对应最小熵值尺度下的连续小波变换系数.对于每一个小波函数，尽管都处于最优车轴识别效果状态，但不一定能够有效地识别出车轴信息.从图14中可以看出，rbio1.3, rbio3.3和rbio3.9的小波变换结果在车轴经过FAD传感器的时刻产生峰值，但由于波峰本身是反对称形状，导致波峰峰值减小，或者如rbio3.9结果所示，一个车轴经过FAD时显现出2个波峰，这都将导致车轴信息难以准确识别.另外如rbio2.8和rbio6.8小波变换结果所示，在由车辆后轴产生的大波峰两侧会出现小波峰，峰值有时甚至大于由车轴产生的小波峰，这也将影响对车轴信息的判断.

事实上，只有 rbio2.2，rbio2.4和rbio4.4小波变换系数显示了2个可识别的波峰且其波峰形状与目标信号相似.本文提出通过计算相关系数来进一步选取小波函数.相关系数计算公式见式(5).

(5)

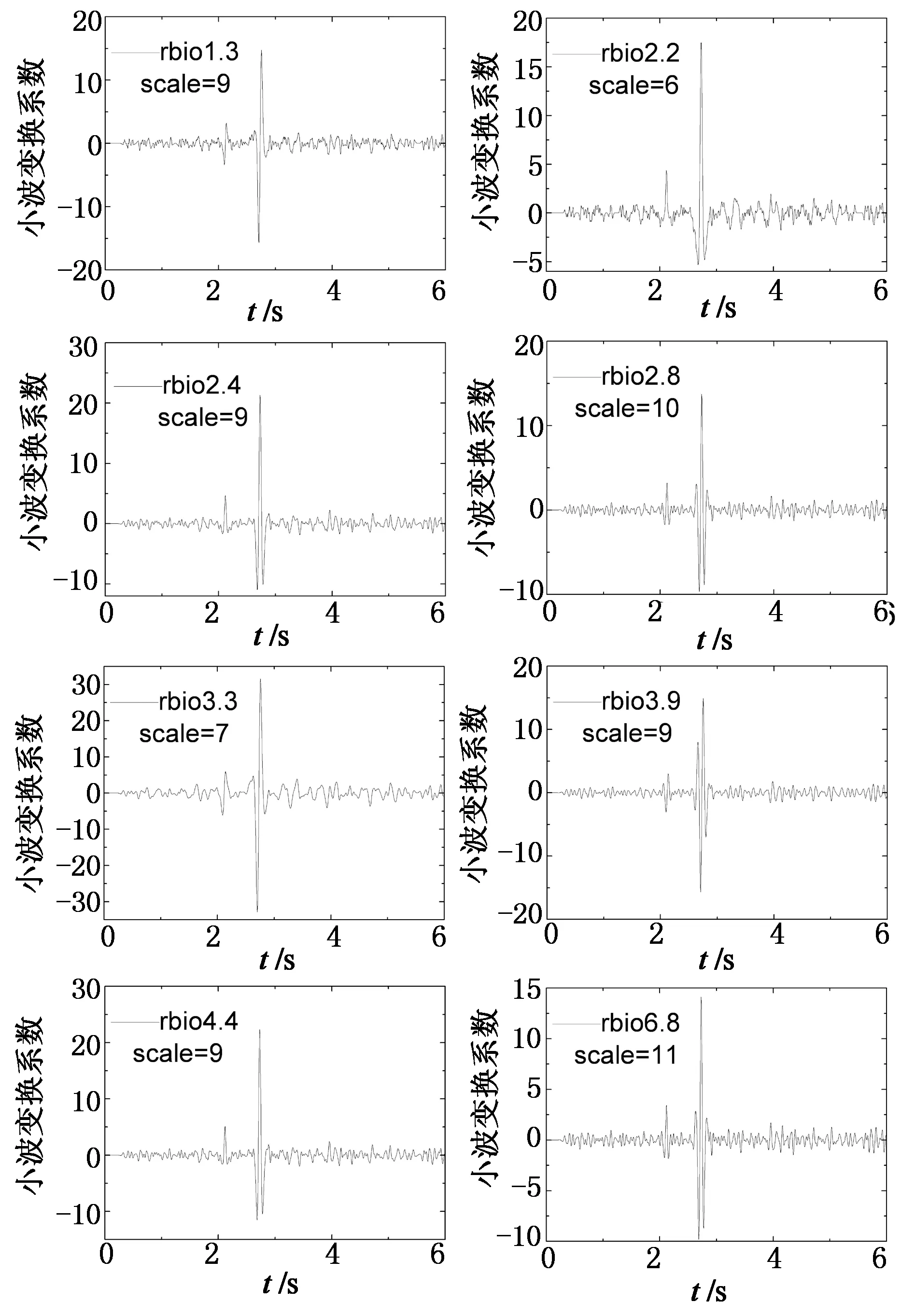
图14　一系列小波函数的连续小波变换结果Fig.14　CWT outcomes from a serial of wavelet functions

由公式(5)计算得到图14中的小波变换结果与L3-FAD1信号的相关系数(图15).识别效果较差的rbio1.3，rbio3.3和rbio3.9小波函数所对应的相关系数很小，不超过0.04；而rbio2.8和rbio6.8小波函数对应的相关系数稍大，但也不超过0.13；车轴识别效果较好的rbio2.2，rbio2.4和rbio4.4小波函数所对应的相关系数均超过0.25，且rbio2.2对应的相关系数达到0.50.

因此，利用小波变换来高效识别FAD车轴信息，可以通过最大相关性和最小Shannon熵值来选取最适合的小波函数及其最佳变换尺度.针对MATLAB中所有常用小波函数，基于上述方法对图11中的FAD信号分别进行小波分析.对于L3-FAD1信号，在rbio2.2且尺度为6时获得最大相关系数以及最小熵值，而L3-FAD2信号，在mexh小波函数尺度为3时获得最大相关系数以及最小熵值.所对应连续小波变换结果如图16所示.这些原始信号经过连续小波变换后，可以很明显地识别出车轴数目，为BWIM系统识别车辆轴重及总重提供前提条件.

小波函数图15　小波变换结果与目标信号的相关系数Fig.15　Correlation between CWT outcomes and FAD signal

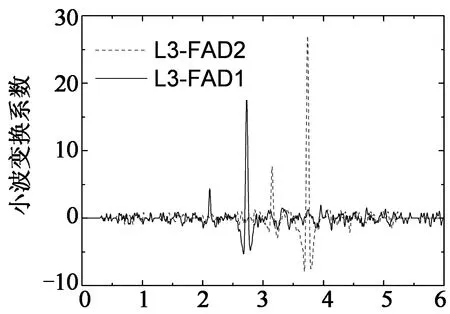
t/s图16　小波变换结果Fig.16　CWT outcomes of measured FAD signals

(6)

在求出速度V后，根据任何一个FAD信号中2个波峰之间的时间差即可计算出轴距，计算公式如下：

(7)

通过公式(6)和(7)可得到车辆的轴间距并和相应的静态测量结果比较，其结果均列在表3中.

表3　连续小波变换计算的轴距

注：L3-FAD1表示的是根据车道3的FAD1传感器计算得到的轴距，其他同理.

3.2.2多辆车同时过桥时FAD信号的小波变换

为了进一步验证小波变换应用于BWIM系统中提高车轴识别效果的有效性，下面利用小波变换识别当两辆车同时行驶过桥时所产生的不易直接获得的车辆信息的FAD信号.

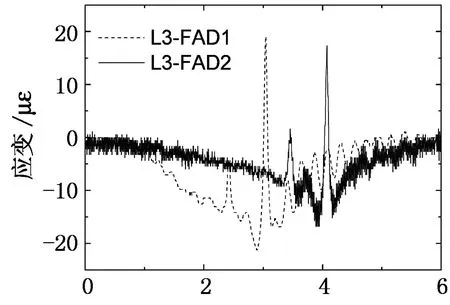
标定车A和B分别同时沿车道4和车道3行驶过桥，对应于这2个车道的FAD传感器L3-FAD1, L3-FAD2, L4-FAD1和L4-FAD2采集的动态应变信号如图13所示.由于试验持续时间长，传感器L3-FAD2工作不稳定，产生了白噪声干扰信号(如图17(a)所示).

t/s (a)第三车道FAD信号

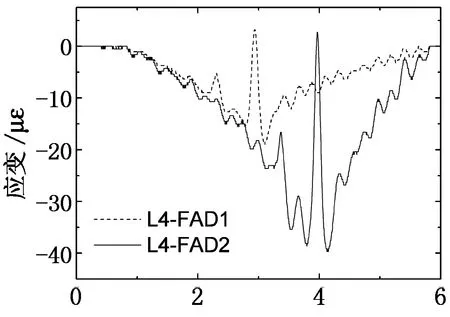
t/s (b)第四车道FAD信号图17　2个车道的FAD原始信号Fig.17　Original FAD signals of two lanes

如图17所示，图中L3-FAD1, L3-FAD2, L4-FAD1和L4-FAD2的信号都只显示出一个峰值信号和一些小波峰，通过这些信号难以直接识别过桥车辆车轴信息，尤其是信号L3-FAD1和L4-FAD2，这种现象更明显.运用上述方法从常用小波函数里面找出最适小波函数分别对2个车道的FAD信号进行连续小波变换，得到的结果如图18所示.尽管信号L3-FAD2掺杂有较大的白噪音信号，在coif1函数尺度14的小波变换下仍能高效识别出车轴信息.另外L3-FAD1, L4-FAD1和L4-FAD2信号分别在rbio2.2尺度为6, gaus2尺度为4和rbio2.2尺度为7时获得理想结果(如图18所示).

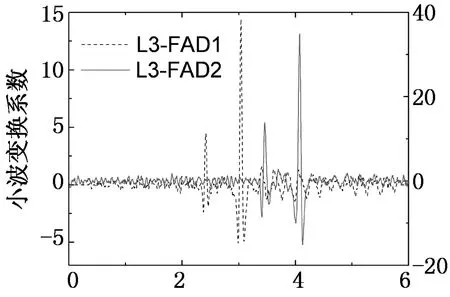
t/s (a) 第三车道FAD信号CWT结果

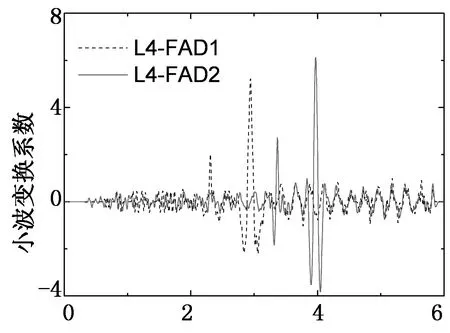
t/s (b) 第四车道FAD信号CWT结果图18　两个车道FAD信号的CWT结果 注：(a)图中左边纵坐标对应于L3-FAD1， 右边纵坐标对应于L3-FAD2)Fig.18　CWT outcomes of FAD signals along two lanes

这些FAD信号在经过连续小波变换后都表现出2个明显的尖峰.对于车道3或车道4，从图18中可明确得到车辆各车轴经过每个传感器的时刻.同样，根据相对应的一对FAD传感器，由公式(6)和(7)可计算出车辆A和B的轴距，结果列于表4.

表4　2辆车同时过桥时由连续小波变换计算的轴距

注：L3-FAD1表示的是根据车道3的FAD1传感器信号计算得到的轴距，其他同理.

4　结　论

1)从数值模拟信号的小波分析结果可以看出，小波变换能够高效率地发现和放大车轴经过传感器时产生的不连续变化斜率，从而准确识别出过桥车辆车轴信息.

2)实桥试验结果分析表明，小波变换能有效解决新型桥梁动态称重(BWIM)系统中部分FAD信号难以直接识别车轴数目、车轴距离及车辆速度的问题.在2组分析例子中，对于所采集的不理想FAD信号，由小波变换所识别的车辆轴距误差在4%以内.

3)在利用小波变换识别车轴信息时，小波变换尺度至关重要，低尺度小波系数显示高频信息，而高尺度小波系数显示低频信息.根据最小Shannon熵的方法得到，只有在使Shannon熵值最小时才能获得最利于识别车轴信息的小波变换尺度.

4)通过对常用的几十种小波函数对同一目标信号进行变换，所得的结果不一致，并且部分小波函数并不能达到预期结果，而只有选取合适的小波函数才能准确地识别车轴信息.依据本文所提出的采用最大相关系数的方法，可以获取最合适的小波函数，从而高效率地识别车轴信息.

5)在新型BWIM系统中，对于那些不能直接识别出车轴信息的FAD信号，小波变换是一个高效而准确地识别车轴信息的工具.在应用小波变换时，首先基于最小Shannon熵值计算出每个小波函数的最适变换尺度，然后求出各最适尺度下的变换系数与目标信号的相关系数，具有最大相关系数者即为最适小波函数.试验证明，对于难以识别车轴信息的FAD信号，依据最小Shannon熵值方法和最大相关系数确定的小波变换系数也能准确、有效地识别车轴信息，进而提高新型BWIM系统识别过桥车辆轴重及总重量的效率和精度.

[1]王迎杰, 沈利平. 浅谈超限运输车辆行驶公路的危害[J]. 交通科技与经济, 2002(3): 41-42.

WANG Ying-jie, SHEN Li-ping. Discussing the damage of the transport vehicle with out-of-gauge goods [J]. Technology & Economy in Areas of Communications, 2002(3): 41-42. (In Chinese)

[2]王锦芳. 动态称重系统的研究与开发[D].杭州:浙江大学控制科学与工程学系,2006:10-17.

WANG Jin-fang. The research and development of dynamic weighing system [D]. Hangzhou: Department of Control Science and Engineering, Zhejiang University, 2006:10-17. (In Chinese)

[3]朱军. 光纤光栅在车辆动态称重系统中的应用研究[D].西安:长安大学工程机械学院，2007:12-15.

ZHU Jun. Fiber bragg grating in the application research of vehicle dynamic weighing system[D].Xi’an:School of Construction Machinery, Chang’an University, 2007:12-15. (In Chinese)

[4]ZNIDARIC A, LAVRIC I, KALIN J,etal. SiWIM bridge weigh-in-motion manual[M]. Slovenian: Slovenian National Building and Civil Engineering Institute, 2005:2-24.

[5]ROB B, PRATT A J. Weigh in motion technology-economics and performance[C]//Presentation on the North American Travel Monitoring Exhibition and Conference (NATMEC), May 11-15, 1998. Charlotte, North Carolina: Federal Highway Administration, 1998: 321-328．

[6]ZHAO H, UDDIN N, O’BRIEN E J,etal. Identification of vehicular axle weights with a bridge weigh-in-motion system considering transverse distribution of wheel loads[J]. Journal of Bridge Engineering, 2014, 19(3): 165-184.

[7]MOSES F. Weigh-in-motion system using instrumented bridges[J]. Transportation Engineering Journal, 1979, 105(3): 233-249.

[8]DUNNE D, O’BRIEN E J, BASU B,etal. Bridge WIM systems with nothing on the road (NOR)[C]//International Conference on Weigh-In-Motion 4th, February 20-23, 2005. Taipei, Taiwan: ARRB Group Limited, 2005: 9-12.

[9]ZHAO H, UDDIN N. Algorithm to identify axle weights for an innovative BWIM system. Part II[C]//Proceedings of IABSE-JSCE Joint Conference on Advances in Bridge Engineering-II, August 8-10, 2010． Dhaka: Bangladesh Group of IABSE,2010:537-546．

[10]ZHANG L X. An evaluation of the technical and economic performance of weigh-in-motion sensing technology[D]. Waterloo, Ontario: University of Waterloo, 2007:5-15.

[11]ZNIDARIC A, LAVRIC I, KALIN J. Bridge WIM measurements on short slab bridges[C]//Weigh-in-Motion of Road Vehicles, WAVE Symposium, Final, May 6-7, 1999． Paris, France: LCPC,1999: 217-225.

[12]PETERS R J. AXWAY—a system to obtain vehicle axle weights[C]//Proceedings of the 12th Australian Road Research Board Conference, 27-31 August 1984. Hobart, Tasmania: ARRB Group Limited, 1984: 10-18.

[13]CHATTERJEE P, O’BRIEN E J, LI Y Y,etal. Wavelet domain analysis for identification of vehicle axles from bridge measurements[J]. Computers & Structures, 2006, 84(28): 1792-1801.

[14]KALIN J, ZNIDARIC A, LAVRIC I. Practical implementation of nothing-on-the-road bridge weigh-in-motion system[C]// International Symposium on Heavy Vehicle Weights and Dimensions, June 18-22 2006, State College．Pennsylvania, USA: IFRTT, 2006: 207.

[15]HAMID K, MOAVENIAN M. A comparative study of DWT, CWT and DCT transformations in ECG arrhythmias classification[J]. Expert Systems with Applications, 2010, 37(8): 5751-5757.

[16]WANG S Y, LIU X, YIANNI J,etal. Extracting burst and tonic components from surface electromyograms in dystonia using adaptive wavelet shrinkage[J]. Journal of Neuroscience Methods, 2004, 139(2): 177-184.

[17]GAO R X, YAN R. Selection of base wavelet[M]. New York:Springer US, 2011:165-187.

Improved Identification of Vehicular Axles in BWIM System Based on Wavelet Transform

ZHAO Hua†, TAN Cheng-jun, ZHANG Long-wei, QIAO Dong-qin

(Key Laboratory for Wind and Bridge Engineering of Hunan Province, College of Civil Engineering, Hunan Univ, Changsha, Hunan410082, China)

In this study, wavelet transform was firstly applied to deal with a numerically simulated signal that was unable to obviously identify axle information. The analysis result showed that the wavelet transform was able to magnify the slope discontinuities so as to accurately identify the silhouette of passing vehicles. Subsequently, based on the field-tested FAD signals through which the vehicle configuration was difficult to be directly identified, the most appropriate transform scales and the best suitable wavelet function performing wavelet transform were selected from the minimum Shannon entropy and maximum correlation. The results demonstrated that the wavelet transform in pattern recognition effectively identified the vehicle configuration (including vehicle velocity, axle numbers, and axle spacing), especially for the unidentified FAD signals. Therefore, wavelet domain analysis can effectively improve the efficiency and accuracy for the vehicular axle identification in BWIM system, and it is beneficial for the successful application of BWIM system in controlling and monitoring overweight vehicles.

bridge weigh-in-motion；axle identification；wavelet transforms；selection of wavelet function；scales

1674-2974(2016)07-0111-09

2015-09-03

国家自然科学基金资助项目(51178178), National Natural Science Foundation of China(51178178); 湖南省自然科学基金资助项目(13JJ2019); 高等学校博士学科点专项科研基金资助项目(20110161120025)

赵华(1975-)，男，湖北荆州人，湖南大学副教授，博士

†通讯联系人，E-mail: zhaohua@hnu.edu.cn

U491；TN911.7

A