波形钢腹板组合箱梁横向受力有效分布宽度研究*

赵　品，荣学亮，叶见曙

(1.东南大学 交通学院, 江苏 南京　210096； 2. 石家庄铁道大学 土木工程学院，河北 石家庄　050043)



波形钢腹板组合箱梁横向受力有效分布宽度研究*

赵品1，2，荣学亮2†，叶见曙1

(1.东南大学 交通学院, 江苏 南京210096； 2. 石家庄铁道大学 土木工程学院，河北 石家庄050043)

为了研究波形钢腹板箱梁的桥面板有效分布宽度，制作了一片模型试验梁，对其进行了静载非破坏性试验，研究了此种结构桥面板的有效分布宽度变化规律.结合现行公路桥规值和有限元结果，在3种有效分布宽度计算值比较的基础上对现行公路桥规值进行修正，得到了不同工况下的有效分布宽度修正系数.结果表明：按现行公路桥规计算的有效分布宽度值相比试验值、有限元结果略小，应对桥规值乘以大于1.0的修正系数，使之适用于波形钢腹板箱梁的有效分布宽度计算.

波形钢腹板箱梁；模型试验；桥面板；有效分布宽度；公路桥规

波形钢腹板箱梁桥面板由波形钢腹板与混凝土板组成的箱梁框架提供弹性约束；波形钢腹板在纵向抗弯刚度、抗剪刚度方面不同于混凝土腹板，与混凝土顶、底板组成的箱梁框架结构的力学特性亦不同于普通混凝土箱梁.与一般的PC箱梁相比，波形钢腹板PC箱梁的抗弯刚度会下降10%, 扭转刚度下降60%, 剪切刚度下降90%[1].因此，波形钢腹板箱梁桥面板的横向受力有效分布宽度必然与混凝土箱梁的桥面板存在一定差异.

目前现行公路桥梁规范(简称桥规)均是针对混凝土T梁桥开口截面的桥面板而言的，都对板的支撑边界条件作了或简支或固支的理想假定.但箱梁顶板与腹板间的连接既不是固支，也不是简支，而是弹性固结的.桥规对行车道板横向受力有效分布宽度的规定，没有区别对待箱梁与肋梁式结构而采取统一规定，而波形钢腹板组合箱梁是由混凝土顶板、混凝土底板和波形钢腹板组成的封闭框架结构.对于波形钢腹板箱梁结构桥面板的有效分布宽度计算，直接采用现行公路桥规的计算公式是否可行，值得深入研究[2-3].

针对上述问题，本文以桥面板的有效分布宽度问题作为研究对象设计制作了一片单箱双室波形钢腹板试验梁，力求在试验研究分析的基础上给出适用于波形钢腹板箱梁桥面板有效分布宽度的计算方法，为工程实际应用提供参考.

1　试验模型

钢筋混凝土肋梁桥桥面板是直接承受车辆轮压的钢筋混凝土板，在构造上桥面板与主梁梁肋和横隔板连接在一起，因此桥面板实际上是周边支撑的板，并有单向板和双向板之分.图1所示的波形钢腹板单箱单室箱梁，通常其横隔板间距la与箱梁横断面腹板的间距lb之比大于等于2，所以称其支撑的桥面板为单向板[4].

为确定上述单向板的横向受力有效分布宽度大小，对1片波形钢腹板试验梁进行了试验研究.

1.1模型概况

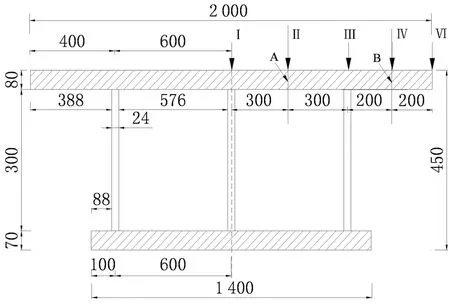
波形钢腹板单箱双室试验梁的截面尺寸和配筋如图2所示.箱梁总长3 500 mm，计算跨径3 300 mm；桥面板横断面宽为2 000 mm，厚度为80 mm.箱梁混凝土的实测立方体抗压强度为28.3 MPa，弹性模量Ec=2.8×104MPa.板内横向受力钢筋的配筋为Ф8@80，屈服强度为327 MPa，极限强度为509 MPa，横向钢筋中心距上缘距离为22 mm；板内纵向受力钢筋的配筋为Ф8@200，屈服强度为327 MPa，极限强度为509 MPa，纵向钢筋中心距上缘距离为26 mm.波形钢腹板采用Q235C钢板，板高300 mm，板厚2 mm，折叠角度37°，波高24 mm，波长144 mm，具体构造如图3(c)所示；试验屈服强度值为194.5 MPa，抗拉强度值为295.1 MPa.

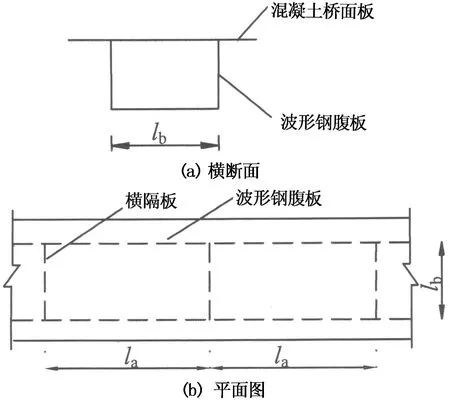
图1　波形钢腹板箱梁横断面及平面图Fig.1　Cross-sectional view and plan view of girders with corrugated steel webs

(a) 跨中断面

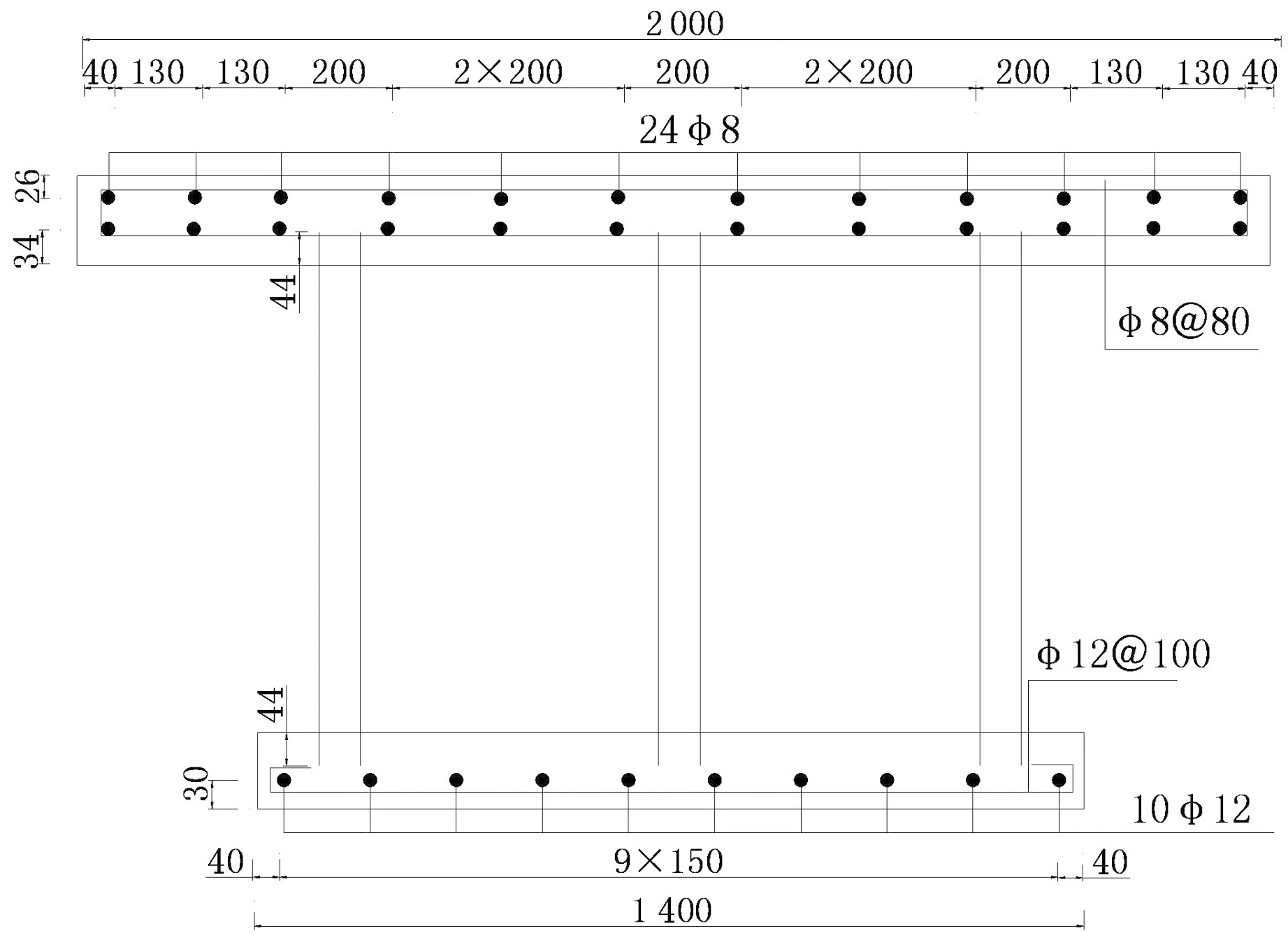
(b) 断面配筋图2　试验梁横断面布置及配筋(单位：mm)Fig.2　Details of cross section and reinforcement of test girder (unit: mm)

在钢腹板上下端插入穿透钢筋与混凝土顶板、底板的构造钢筋绑扎在一起来构成整体, 如图3(a)所示，其抗剪连接构造如图3(b)所示.

(a) 波形钢腹板立面图

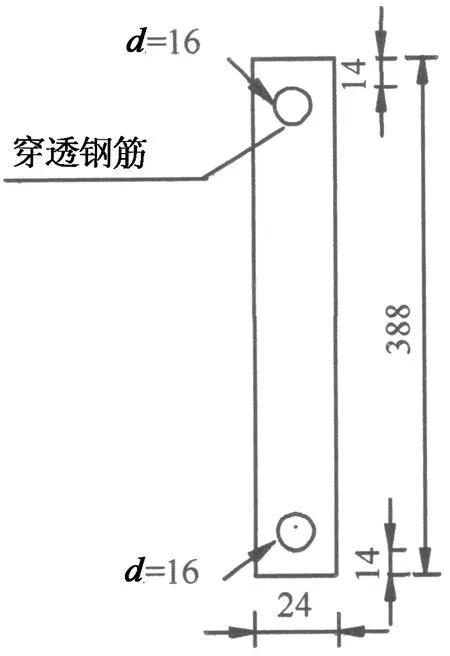
(b) 试验梁抗剪连接构造

(c) 波形钢腹板详图图3　波形钢腹板构造(单位：mm)Fig.3　Structural map of corrugated steel webs (unit: mm)

1.2加载布置和测试布置

加载所用条形钢板平面尺寸定为200 mm×200 mm，厚度定为10 mm.试验加载装置如图4所示.

图4　试验加载装置Fig.4　Experimental setup under static load

本试验为静载作用下的非破坏性试验，利用反力架和油压千斤顶对试验梁进行加载；采用与反力架接触的压力传感器控制试验加载吨位[5].

为了研究波形钢腹板单箱双室箱梁桥面板在车轮荷载作用下的有效分布宽度值，试验梁的加载桥面板分为箱梁腹板间的桥面板及悬臂板.并针对板的荷载有效分布宽度规定中的一个车轮荷载、两个车轮荷载，设定相应的试验加载工况有纵向单点加载和纵向双点加载(0.5 m分配梁加载)，如图4所示.横向加载位置有中腹板处加载(工况Ⅰ)、A-A截面加载即边腹板与中腹板间的桥面板跨中位置加载(工况Ⅱ) 、边腹板处加载(工况Ⅲ) 、B-B截面加载即悬臂长度的1/2位置加载(工况Ⅳ) 、悬臂翼缘端部加载(工况Ⅴ)，如图2(a)所示.加载方式为分级加载，加载最大载荷根据加载工况的不同而异，分别为40, 25, 20, 10, 8 kN.

为测得箱梁的横向内力分布曲线，分别在箱梁边腹板、中腹板间的桥面板跨中位置、悬臂长度的1/2位置、悬臂翼缘端部及腹板与顶板相交部位下沿纵向以跨中位置为中心向两侧各1 m长的梁段，每隔20 cm布设一组横向应变片.

在箱梁的跨中及支座位置布设千分表和百分表以测得梁体在加载过程中的支座沉降、挠度及梁体的扭转角位移.

2　局部荷载下的桥面板有效分布宽度

在有效分布宽度概念及计算规定的基础上，将模型梁的试验数据按照有效分布宽度定义计算出各工况下的有效分布宽度值.根据桥规中单向板荷载有效分布宽度的几种工况，即：①车轮荷载作用在板跨径中间；②车轮荷载作用在板的支撑处；③车轮荷载靠近板的支撑处.对应的试验工况分别为：工况Ⅰ中腹板处加载即为荷载作用于顶板横截面中心；工况Ⅱ中A-A截面加载即为荷载作用于边、中腹板中间位置的顶板上；工况Ⅲ边腹板处加载即为荷载作用于边腹板位置处的顶板上.同时针对悬臂板荷载有效分布宽度的工况有工况Ⅳ即B-B截面加载，工况Ⅴ即悬臂翼缘端部加载[6-12].

按照文献[4]中对行车道板及悬臂板的受力状态描述，令板的计算跨径L为单箱双室箱梁任一室中的两腹板间距，L0为悬臂翼板的宽度；a1和b1分别为试验中条形钢板的平面尺寸.

单点加载时5种横向不同加载位置作用下沿波形钢腹板单箱双室箱梁桥面板纵向的横向应力试验值如图5所示.其中中腹板处加载、A-A截面加载、边腹板处加载时的数值指的是荷载作用位置处的有效分布宽度值；B-B截面加载、悬臂翼缘端部加载时的数值为悬臂翼缘根部的有效分布宽度值.图中沿纵向的横向应力值分布分别对应各工况最大弹性加载值作用下所产生的应力值，不同图中的数据不作对比.

从图5中可看到，由波形钢腹板与混凝土底板所组成的框架结构支撑的混凝土桥面板在荷载作用下的横向应力分布呈曲线形式分布，且在荷载中心处达到最大值.同于普通混凝土桥面板的相应应力分布形式.

在计算局部荷载作用下顶板的有效分布宽度时，可按公式(1)采用测得的混凝土应变积分来求解.

(1)

式中：M为局部荷载所产生的沿纵向的横向总弯矩；mxmax为沿纵向板带的横向单宽弯矩峰值；εx为实测的箱梁顶板产生的横向应变值；εxmax为实测的箱梁顶板产生的最大横向应变值；a为箱梁顶板有效分布宽度.

可得到图5所示荷载作用下的有效分布宽度计算值，见表1.表1给出了纵向不同位置在单、双点加载方式下的有效分布宽度值.从表1中可看出：荷载由中腹板位置向边腹板位置移动时，有效分布宽度先增大再减小，即中腹板处加载时的有效分布宽度大于边腹板处加载时的相应值；荷载作用于悬臂翼板位置时，翼板端部的有效分布宽度大于悬臂翼板B-B截面的相应值，同于文献[7]的结论.

同一荷载值的双点加载时(即在荷载总值不变的情况下将单点荷载分为间隔为50 cm的双点荷载)，5种工况下的有效分布宽度值均大于单点加载时的有效分布宽度值.

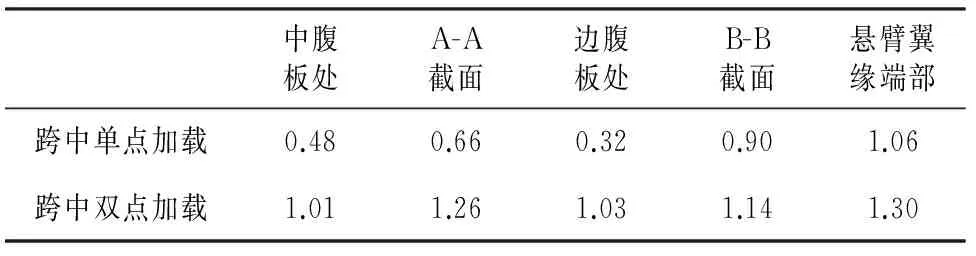
表1　有效分布宽度计算值

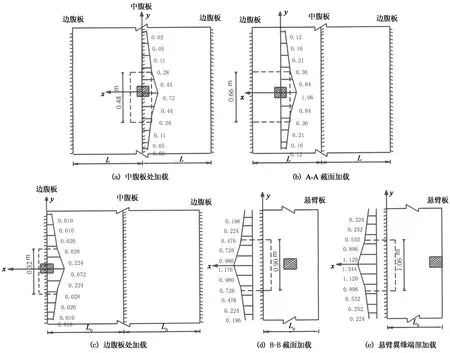
图5　跨中单点加载时的桥面板横向应力 (单位：MPa)Fig.5　Transverse stress of deck under midspan section single point load (unit:MPa)

3　波形钢腹板箱梁桥面板的有效分布宽度分析

3.1试验梁结果

在上述试验梁结果的基础上将分别采用有限元法和桥规方法对波形钢腹板箱梁桥面板的有效分布宽度进行分析.公路桥规对板的支撑边界条件作了或简支或固支的理想假定；而试验方法与有限元法针对单箱双室箱梁结构中的顶板，考虑了波形钢腹板、底板形成的框架结构对顶板的支撑.针对上述两类计算方法原理的差别，本文对试验值、有限元结果及现行公路桥规值进行了对比分析，结果见表2.

其中有限元分析是采用通用软件ANSYS12.0建立试验梁的数值模型，在模型中分别采用实体单元Solid95模拟混凝土顶、底板，板壳单元Shell63模拟波形钢腹板；上述两类单元采用节点耦合法连接.然后根据此模型计算波形钢腹板箱梁桥面板的横向应力值.

因局部荷载值大小对箱梁有效分布宽度值影响很小，故5种不同工况下的有效分布宽度值可做比较[7].

由表2可知，无论单点加载还是双点加载，按现行公路桥规的计算值、有限元值与试验值的变化趋势相同，即采用前两种方法得出的有效分布宽度值变化规律同于表1的分析结果.

以试验值为基准，通过有限元值、桥规值与试验值的对比可知，有限元结果与试验结果较接近，桥规值相比二者均较小，比较保守.

近处的稻草依然微黄，在风中摇曳着。天色渐暗。这个村庄、这样的情境百多年来日复一日，似乎已经在这里等待我们很久。而我们来到这里的这一刻，却只是一闪即逝的瞬间。面对这样的情景，我们有些兴奋，有些赞叹，有些感慨，也有些怆然。村里人不多，暮色下格外的宁静安详。

表2　波形钢腹板单箱双室试验梁顶板的有效分布宽度

3.2实桥结果

同时以某实桥为对象分析顶板的有效分布宽度，该桥上部结构形式采用单箱双室波形钢腹板预应力简支组合梁结构，跨径为50 m，具体横断面尺寸见图6.

纵向加载位置为跨中截面附近，横向加载工况同于试验梁中的5种工况.荷载采用公路Ⅱ级加重车后轴中的单个轮载和间距为1.4 m的2个轮载分别作为单点荷载(单轮荷载)、双点荷载(双轮荷载).

同于试验梁应变片的布置方式，亦分别在实桥箱梁边腹板、中腹板间的桥面板跨中位置、悬臂长度的1/2位置、悬臂翼缘端部及腹板与顶板相交部位下沿纵向每隔2 m布设一组应变片，沿纵向共布设10组.

图6　横断面图(单位：cm)Fig.6　Cross-sectional view (unit: cm)

分别采用有限元法、试验方法和现行公路桥规法对桥面板有效分布宽度进行分析，其结果见表3.

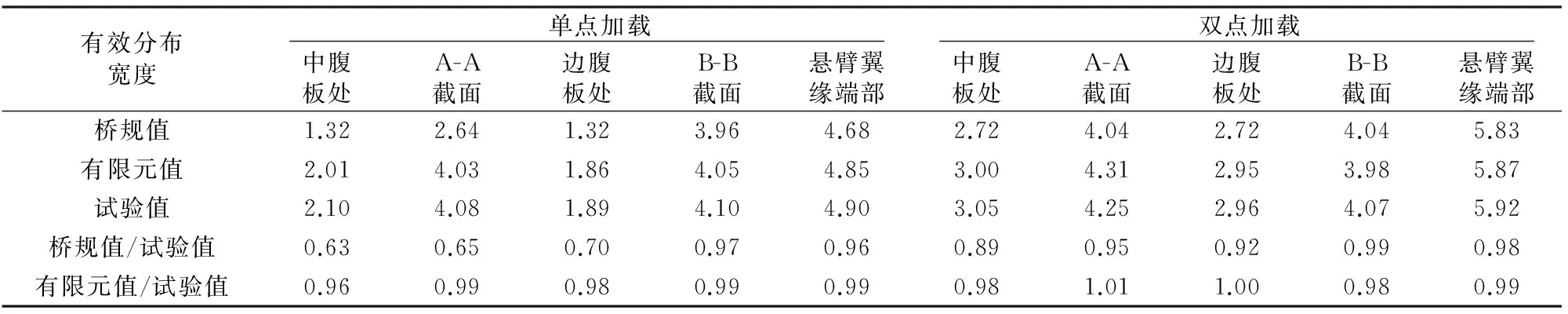
表3　波形钢腹板单箱双室实桥箱梁顶板的有效分布宽度

同样以试验值为基准，通过有限元值、桥规值与试验值的对比得出与试验梁相同的结论, 即桥规值相比有限元结果、试验结果均较小，比较保守.

以上述实桥中单室的桥面板在单轮荷载和双轮荷载下修正后的桥规值示于图7.

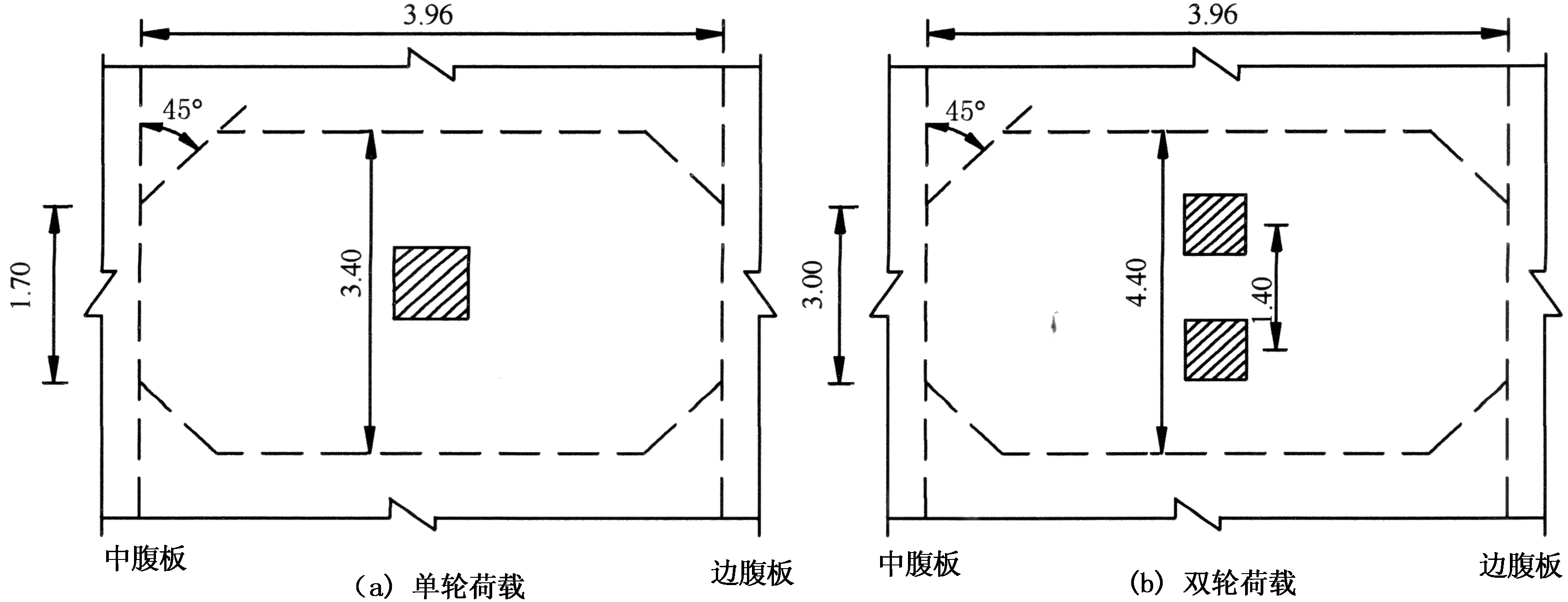
图7　单轮和双轮荷载作用下的有效分布宽度 (单位：m)Fig.7　Effective distribution width under a single wheel and two wheel loads (unit: m)

由图7可见，修正后的有效分布宽度值从板的支撑处到跨径中间仍近似按45°线过渡.

4　结　论

根据混凝土桥面板横向应力分布和有效分布宽度的综合分析，可得出以下结论：

1) 无论是单点加载还是双点加载，现行公路桥规值、有限元值与试验值的结果变化趋势相同，均为：荷载由中腹板位置向边腹板位置移动时，有效分布宽度先增大再减小，即中腹板处加载时的有效分布宽度大于边腹板处加载时的相应值；荷载作用于悬臂翼缘位置时，翼缘端部的有效分布宽度大于悬臂翼缘B-B截面的相应值.

2) 我国现行桥规针对混凝土T梁桥开口截面的桥面板而言，假定板的支撑边界条件为简支或固支；而试验方法、有限元法针对单箱双室箱梁结构中的顶板，考虑了波形钢腹板、底板形成的框架结构对顶板的支撑.采用3种计算方法对试验梁、实桥分别进行了分析，得出相同的结论：桥规值相比有限元值、试验值而言比较保守.

3) 波形钢腹板箱梁桥面板的有效分布宽度值的变化规律同于混凝土桥面板的变化规律，同为从板的支撑处到跨径中间近似按45°线过渡.

[1]陈宜言．波形钢腹板预应力混凝土桥设计与施工[M]．北京：人民交通出版社，2009：1-10．

CHEN Yi-yan. Design and construction of prestressed concrete bridge with corrugated steel webs[M]. Beijing: China Communications Press, 2009：1-10.(In Chinese)

[2]JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S]．北京：人民交通出版社，2004：14-22．

JTG D62—2004Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S]. Beijing: China Communications Press, 2004:14-22. (In Chinese)

[3]程翔云．梁桥理论与计算[M]．北京：人民交通出版社，1986:74-107．

CHENG Xiang-yun. Theory and calculation of the beam bridge[M]. Beijing: China Communications Press,1986:74-107.(In Chinese)

[4]项海帆．高等桥梁结构理论[M]．北京：人民交通出版社，2001:1-14．

XIANG Hai-fan. Advanced structure theory of bridges [M]. Beijing: China Communications Press, 2001:1-14. (In Chinese)

[5]方志，郑辉，刘双阳．基于塑性分析的钢筋混凝土箱梁悬臂板横向受力有效分布宽度[J]．土木工程学报，2012，45(3) ：35-41．

FANG Zhi, ZHENG Hui, LIU Shuang-yang. Plastic analysis of the lateral effective width of cantilever slabs of reinforced concrete box-girders[J]. China Civil Engineering Journal, 2012, 45(3):35-41. (In Chinese)

[6]方志，张志田．钢筋混凝土变截面箱梁横向受力有效分布宽度分析[J]．湖南大学学报:自然科学版，2003，30(6)：82-85．

FANG Zhi, ZHANG Zhi-tian. Effective distribution width of the transverse internal force in R-C box girders with varied section[J]. Journal of Hunan University: Natural Sciences, 2003, 30(6):82-85.(In Chinese)

[7]刘清．波形钢腹板组合箱梁横向内力理论及试验研究[D]．长沙：湖南大学土木工程学院，2009: 9-16．

LIU Qing．Theoretical and experimental study on the transverse internal force of the composite box girder with corrugated steel webs[D]．Changsha：College of Civil Engineering, Hunan University，2009: 9-16.(In Chinese)

[8]聂建国，朱力，唐亮．波形钢腹板的抗剪强度[J]．土木工程学报，2013，46(6): 97-109．

NIE Jian-guo, ZHU Li, TANG Liang. Shear strength of trapezoidal corrugated steel webs[J]. China Civil Engineering Journal, 2013,46(6): 97-109.(In Chinese)

[9]ELGAALY M，SESHADRI A．Girders with corrugated webs under partial compressive edge loading[J]. Journal of the Structural Division，ASCE，1997, 122(4): 783-791．

[10]BAKHT B. Simplified analysis of edge stiffened cantilever slabs[J]. Journal of the Structural Division, ASCE, 1981, 107(3)：535-550.

[11]徐岳，朱万勇，杨岳．波形钢腹板PC组合箱梁桥抗弯承载力计算[J]．长安大学学报: 自然科学版，2005，25(2)：60-64．

XU Yue, ZHU Wan-yong, YANG Yue. Calculation of ultimate moment capacity of prestressed concrete box-girder bridge with corrugated steel webs[J]. Journal of Chang’an University: Natural Science, 2005,25(2):60-64. (In Chinese)

[12]张阳，邱俊峰，唐重玺．部分波形钢腹板预应力连续组合梁性能分析[J]．湖南大学学报:自然科学版，2013，40(12)：14-20．

ZHANG Yang, QIU Jun-feng, TANG Chong-xi. Analysis of behaviors of prestressed steel-concrete continuous composite beam with partial corrugated steel webs[J]. Journal of Hunan University: Natural Sciences, 2013, 40(12): 14-20.(In Chinese)

Research on the Lateral Effective Width of CompositeBox-girders with Corrugated Steel Webs

ZHAO Pin1,2，RONG Xue-liang2†，YE Jian-shu1

(1. School of Transportation, Southeast Univ, Nanjing, Jiangsu210096, China;2. School of Civil Engineering, Shijiazhuang Tiedao Univ, Shijiazhuang, Hebei050043, China)

One model test beam is made to study effective distribution width of the deck of girder with corrugated webs. Then static non-destructive testing is conducted to study distribution of transversal force of this structure. And by combination to the current road bridges criterion value and data of finite element analysis, on the basis of comparetion of three kinds of effective distribution width values, the road bridges criterion value was modified and the effective distribution width correction coefficient under different loading conditions was obtained. And the results demonstrated that the road bridges criterion value was smaller than test results and data of finite element analysis, in order to apply to the effective distribution width calculation of box girder with corrugated steel webs, the former should be multiplied by the coefficient of more than 1.0.

box girders with corrugated steel webs; model tests; bridge decks; the effective distribution width; the road bridges criterion

1674-2974(2016)07-0105-06

2015-08-07

国家自然科学基金资助项目(51508348), National Natural Science Foundation of China(51508348)

赵品(1982-)，女，河北石家庄人，博士，讲师

†通讯联系人，E-mail:rongyihit@126.com

U448.21

A