基于Petri网的最短路径算法的研究

段任航，赵佩斯

（桂林电子科技大学 电子工程与自动化学院，广西 桂林　541004）

基于Petri网的最短路径算法的研究

段任航，赵佩斯

（桂林电子科技大学 电子工程与自动化学院，广西 桂林541004）

研究寻找交通最短路径问题。传统的最短路径算法存在计算量大，效率低下等问题。为了更好地求出实时交通状态下的最短路径，在先前最短路径的研究基础上，提出了基于Petri网的最短路径搜索算法。该算法可以根据现有的交通路线图进行建模，再根据实时道路的交通状况对建模图进行修改和仿真。在减少计算量的同时，使仿真求出的结果更符合真实的交通状况。实验结果证明，新算法和经典Dijkstra算法相比，计算量显著减小可以明显提高现实路径的搜索效率。

Petri网；交通网络；最短路径；扩充托肯；变迁权值；实时路况；粘滞因子

近年来，随着人民生活水平的提高，城市规模的不断扩大，人们出行的需求也日益增加，交通运输事业面临着前所未有的压力:车辆拥挤严重、交通事故频发、道路环境持续恶化。为解决现实的交通问题，最短路径的研究日益受到大家的重视。最短路径研究和现实生活中很多重要事物有着非常密切的关系。例如，城市公交的最短路径搜索系统，紧急救援的公共安全系统，城市水供、电供及气供线路的规划和设计系统等[1]。然而由于各种各样的技术原因，现有的交通运输服务体系不能满足人们的实际出行需求[2]。文中主要结合Petri网的理论知识和建模方式将现实的交通运输网络转换为Petri网表示的有向图，求出相应的运输网络中最短有向路径及行驶时间。

现有的分析最短路径的方法可分为两类，一类是运用图论去分析问题，比较常见的有：Dijkstra算法、SPFA算法、Floyd算法等；一类是运用网论去分析问题。针对最短路径算法的研究国内主要有：高明霞[3]为网络中的各个弧设置了一个距离标号和紧前弧标号，通过不断迭代，，更新弧的标号来寻找最短路径。郑年波[4]将交通路网表达为动态对偶网络，推导了满足先进先出特性的动态行程计算方法，设计了时间依赖的标号设定最短路径算法。唐小勇[5]和杜牧青[6]从数据存储结构和算法两方面着手求解最优路径。

物流配送路径选择是典型的离散事件系统，选择 Petri网对物流配送路径选择进行模拟比较合适[7]。文中就是运用一定程度上改进的Petri网方法。文章首先简单介绍了Petri网的基本原理和概念，然后将现有的路线图转化为有向的网络图，运用Petri对有向网络进行分析，最终求得所需的最短路径。本方法不仅能准确求得最短路径，而且在实用方面比传统的方法更为优越。

1　Petri网的交通网络建模

1.1Petri网概述

Petri网是一种网状的信息流模型，是一种适合于并发、异步、分布式软件系统规格与分析的形式化方法，也是一种进行系统分析和模拟的图形化建模的工具，由表示状态的元素库所P（Place）和表示状态变化的元素变迁T（Transition）[8]两类元素组成。

其中网的部分描述系统的结构，标识部分表示系统的状态。通常，小圆圈表示库所用来决定变迁是否使能，而小方框表示变迁用以改变系统的运行状态。库所与库所之间，变迁与变迁之间不能有依赖关系。

1.2扩充Petri网

本文需要对日常的公共交通运用Petri网进行仿真建模，考虑到如果只用最基本的Petri网难以描述和计算，因此有必要对托肯和变迁的使能规则进行扩展。

首先对Petri网的托肯进行附加描述。平常的Petri网图中的托肯只有一种状态，用库所中的小实心“·”表示。现在再赋予其另外一个描述，用空心“△”表示。该托肯表示该库所的输入集合·Pi变迁发生，但车辆尚未驶入该库所，如图1所示。

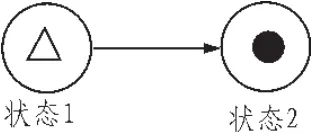
图1　托肯的状态变化Fig.1　Token of status change

状态1表示，该库所的输入变迁已经发生，车辆从前一个地点出发，正在赶往该地点的路上，状态2表示车辆已经到达了库所。

然后，对变迁规则进行新的定义：

规则1：当库所Pi处于状态2时，托肯的运行方向由集合R′i决定。R′i=Ri-（RiI B），其中Ri是符合行驶方向的所有通过变迁与Pi相连接的库所集合，B是已有托肯进入或通过的库所集合。

规则2：当库所Pi处于状态2时，托肯立即驶出不在库所停留，表明车辆不会在非目的地停留。

规则3：若库所Pi的状态由1变成2，则该库所的·Pi里面的其余托肯移除网路，说明起点到该库所的最短路径已找到，其他到该库所的路径舍去。

规则4：当目标点终点库所的状态变成2的时候，算法结束，得出所求的最短路径。

1.3交通运输网络的Petri网表示

Petri网是由（S，T；F）决定的二元图，图2是一个简单的路径图进行Petri网建模的结果，库所代表路径图的站点，变迁代表节点之间的道路，变迁上的权值代表按标准行驶速度（40 km/h）行驶完该路段所需的时间。下图是根据现有的路径图进行建模的结果，路径图上所有站点和路径信息都完整的显示在了图上。

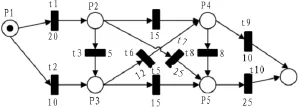
图2　路径图Petri网建模Fig.2　Roadmap Petri net modeling

上图是由实际的6个站点和10条道路的Petri建模图，站点抽象的库所集

P={P1，P2，P3，…P6}，道路抽象为变迁集T={t1，t2，t3，…t10}。变迁上的权值是走完该道路所需的单位时间。变迁的权值集W={w1，w2，w3，…w10}。

1.4实时道路状态反馈思想

路径问题不能局限于地理意义上的距离上的最短，理论上距离最短的路径可能实际上不是最优路径[9]，所以应将通过所选道路所需的实际时间作为物流调度算法的主要考虑因素。这里将道路的交通状况作为考虑因素。文中在此提出一个粘滞因子β，β∈[1，+∞）。

我们根据公共交通的现实情况，将默认的车辆行驶标准速度定为40 km/h，则根据实时的交通情况定义如下：

1）通畅：v0≥40 km/h，β=1；

2）轻度拥挤：40 km/h>v0≥30 km/h，β=2；

3）拥挤：30 km/h>v0≥20 km/k，β=4；

4）重度拥堵：20 km/h>v0≥10 km/h，β=8；

5）堵塞：v0<10 km/h，β=∞。

这样，便可根据实时的道路交通状况来确定粘滞因子β的值，将得出的值参与到后续计算的考虑之中。下图在图2的基础上通过添加β来还原实际交通状况。

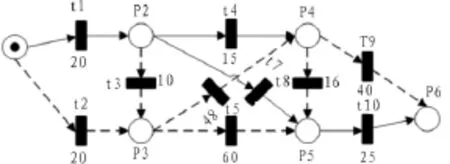
图3　加入粘滞因子后建模图Fig.3　After adding sticky factor modeling diagram

上图可知，根据后加入的粘滞因素β，反馈后的权值集合

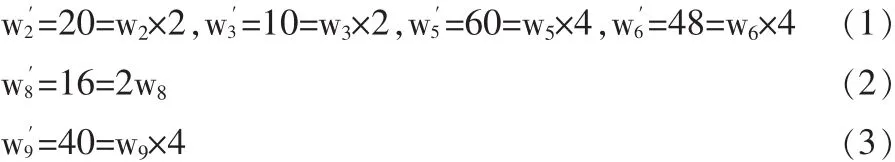
从反馈可得知，t2，t3，t5，t6，t8，t9路段道路发生了拥堵和不畅，这样文中在进行算法研究时可及时避开拥堵路段，为后续工作提供保障。

2　最短路径Petri网仿真算法

2.1算法原理

该算法将已知的路径图进行Petri网建模，用Petri网将复杂的交通路径用简洁的方式表示出。再通过1.3节提出的粘滞因子对已有的Petri网模型进行变迁权值的修改，真实还原实际的道路交通状况。1.2节中的变迁规则避免了一些无意义的查找，保证了算法的计算效率，当目标库所的状态变为状态2时，整个算法结束，得到最短路径序列。

2.2算法的具体步骤

步骤1：根据路径图对其进行Petri建模，其中将路径图中的站点抽象为库所集合，将连接各站点之间的道路抽象为变迁集合，站点之间的距离抽象为变迁上的权值集合；

步骤2：根据1.3节提出的粘滞因素β和前方实时得知的交通情况对建立好的Petri网模型进行相应的变迁权值修改；

步骤3：起始库所中托肯的状态变为状态2，算法开始。起始库所进入集合B，与起始库通过变迁相连的库所托肯状态变为状态1；

步骤4：若库所中托肯状态从状态1变成状态2，则该库所进入集合B，与之相连的符合规则的输出变迁集合使能，相应的库所变成状态1，开始路途耗时，直到托肯进入相应库所；

步骤5：处于状态1的库所Pi如果∈B，则其输入变迁集合·Pi不使能，否则正常使能；

步骤6：当目标库所的托肯状态变为状态2时，算法结束，否则回到步骤4直到目标库所托肯状态变成2。

如图4所示为本算法的具体流程图。

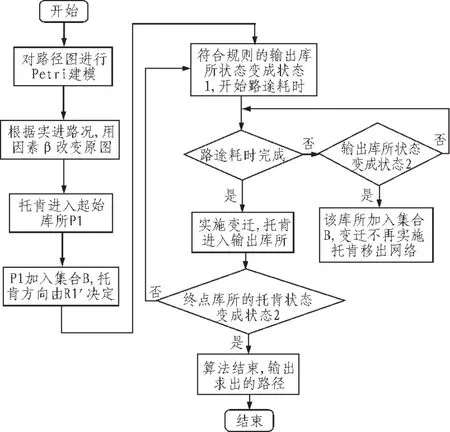
图4　最短路径算法流程图Fig.4Shortest path algorithm flowchart

2.3算法应用实例

图5是某地方的交通地图，起点是①，目的地是輥輰訛，线段代表点之间的路，线上的数字代表通过该路段所需的单位时间（按速度40 km/h计算）。本节使用Petri网对其进行建模，并与下节的经典Dijkstra算法求解进行对比，以此来论证算法的可行性、实用性。

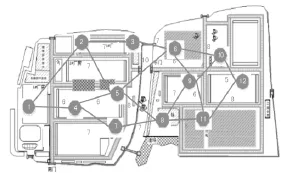
图5　某地区的交通地图Fig.5　Traffic map of an area

2.3.1Petri网最短路径算法

由图5可知，起始地点是①，目标地点是輥輰訛，则对该图所建模型如图6。

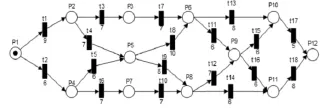
图6　交通地图的Petri网表示Fig.6　Traffic map Petri net representation

此时根据前方提供的最新道路状况得知，从②和③，④和⑤，⑤和⑧之间的道路出现拥堵，其平均速度分别是：22 km/h，20 km/h，26 km/h；①到④，③和⑥，⑥和⑩之间的道路出现轻度拥堵，其平均速度是35 km/h，32 km/h，33 km/h；⑧和輥輯訛，輥輯訛和輥輰訛之间的道路出现重度拥堵，其平均速度是15 km/h，12 km/h，其余路况正常。则文中根据粘滞因素β对建立好的Petri网模型进行相应的变迁权值修改，修改后的图如下。

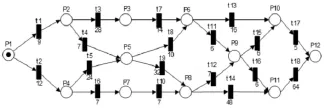
图7　修改权值后的Petri网图Fig.7　Right to amend the Petri net value

修改后的权值表示按照现在的交通状况，走完相应道路所需的单位时间。现在根据2.2节的步骤按步进行算法的仿真，由于篇幅限制，在此只写出几个具有代表性的单位时间，对应的其中时刻由图8所示。

1）时刻0，图8（a），此时算法开始，集合B=覫，R′1={P2，P4}。如图8（a），P2和P4的托肯进入状态1，此时路途耗时开始，P1加入集合B；

2）时刻9，图8（b），此时库所P4中的托肯进入状态2，B= {P1，P2}，R′2={P3，P5}其的输出变迁t3和t4使能，而库所P4中的托肯还处于状态1，路途耗时还有单位时间3；

3）时刻 12，图8（c），库所P4中托肯进入状态2，B={P1，P2，P4}，R′4={P5，P7}其输出变迁t5和t6使能。此时P3和P5中托肯处与状态1，路途耗时分别还有单位时间25和5；

4）时刻 16，图8（d），库所P5中托肯进入状态2，B={P1，P2，P4，P5}，R′5={P6，P8}其输出变迁使能，并且因为此时 P4到 P5路途耗时还未结束，R′4I B={P5}，所以·P5中的变迁t5结束使能。P3和P7的路途耗时分别是单位时间21和3；

5）以此类推，当一个托肯提前完成行程到达指定位置的时候，尚在行程中的托肯结束计算，以此保证不重复运算。图2.5（e）中时刻26，库所P8中的托肯进入状态2，B={P1，P2，P4，P5，P6，P7，P8}，R′8={P9，P11}。此时因为P8∈B，而P5到P8的托肯还在进行路途耗时，所以变迁t9，终止使能。同时P6中的托肯进入状态2；

6）时刻43，图8（f），目标库所中的托肯进入状态2，此时算法结束，还在路途耗时的相关变迁全部结束，托肯移出网络，B={P1，P2，P4，P5，P6，P7，P8，P9，P10，P11，P12}，而求得的最短路径是P1→P2→P5→P6→P9→P10→P12，即求得从地图①～輥輰訛的最短路径是①→②→⑤→⑥→⑨→⑩→輥輰訛。需花费43个单位时间到达。

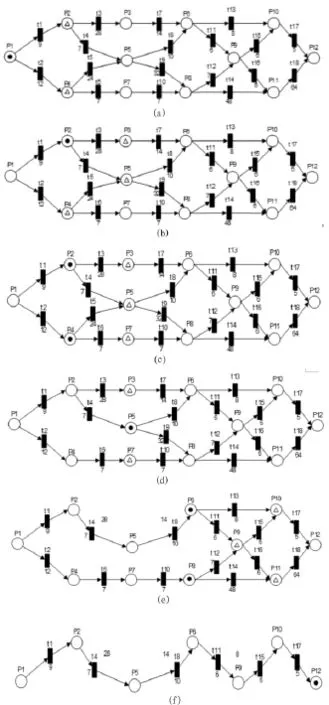
图8　不同时刻对应的Petri网图Fig.8　Different times corresponding Petri net

2.3.2经典Dikstra算法

经典Dikstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。其的主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止[10]。

寻找从①到輥輰訛的最短路径，各个线段上的权值表明距离值，用Dijkstra算法求最短的路径表示如下：

定义集合S和集合U，初识状态下S={①}，U={②，③，④，輥輰訛}。在集合U中找出距离出发点①最近的点，加找出的点加入集合S，再以新加入的点为中间点去寻找离出发点最近的点，周而复始，直到终点輥輰訛加入到集合S，算法停止，输出最短路径。

限于篇幅，具体过程略过。最终求得S={①，④，⑤，⑧，輥輯訛，輥輰訛}，所以得出①到輥輰訛的最短路径是：①→④→⑤→⑧→輥輯訛→輥輰訛。

2.4算法优越性分析

由2.3节可知，运用基于Petri网的算法求得的最短路径是①→②→⑤→⑥→⑨→⑩→輥輰訛，而通过经典Dikstra算法求得的最短路径是①→④→⑤→⑧→輥輯訛→輥輰訛。根据实时的交通状况可知，从②和③，④和⑤，⑤和⑧之间的道路出现拥堵，①到④，③和⑥之间的道路出现轻度拥堵，⑧和輥輯訛，輥輯訛和輥輰訛之间的道路出现重度拥堵。经典Dikstra算法求出的最短路径，正好经过了出现拥堵和重度拥堵的④和⑤，⑤和⑧，⑧和輥輯訛，輥輯訛和輥輰訛之间的路段（时速30 km/h>v0≥20 km/h和20 km/ h>v0≥10 km/h）。所以，实际应用中极容易导致车辆行驶进入堵塞路段，影响正常的出行计划。经典Dikstra算法求解的过程中通常需要遍历所有点，在数据庞大的背景下，计算的效率比较低下。

本文提出的基于Petri网的算法避开了这些路段，且在计算的过程中有选择性地排除了一些路线，避免了重复运算，可较快地求出最短路径，更可以避免出现车辆驶入已出现堵塞的道路，造成不必要的损失。

3　结束语

在研究最短路径问题上，文中提出了基于Petri网的最短路径算法。其面向的是实时交通网络，可根据实时的交通状况，改变建模的图，还可实现通行过程的动态模拟，找出最优路径。与经典Dijkstra算法相比，本文提出的算法更简便，灵活度好且运行效率高。其使能规则的更是有效的降低了通行路网上路径选择的复杂度，缩小了搜索范围，避免了很多无意义的寻找提高了查找效率。在交通日益拥堵的今天，本算法更可以通过实时的交通状况，提前避开可能出现堵车的路段，具有很强的实际意义。

[1]Fang MeiHong，Liu ShaoHua.The design and realization of the shortest path algorithm based on VC++[J].Urban Geotechnical investigation&surveying，2008（1）:43-46.

[2]YAN Han-Bing，LIU Ying-Chun.A New Algorithm for Finding Shortcut in a City's Road Net Based on GIS Technology[J].Chinese Journal of Computers，2000，23（2）: 211-215.

[3]高明霞，贺国光.考虑交叉口延误和转向限制的弧标号最短路径算法[J].兰州交通大学学报，2011，30（6）:111-114.

[4]郑年波，陆锋，段澄澄.道路转向延迟的动态对偶图模型[J].中国图象图形学报，2010，15（6）:915-920.

[5]唐小勇，程琳，徐上.考虑转向延误最短路径算法及实现[C].南京:第三届中国智能交通年会论文集，2007.

[6]杜牧青，程琳.考虑交叉口转向延误[J].西南交通大学学报，2010，45（2）:249-254.

[7]罗义学.基于智能Petri网的物流配送路径优化算法[J].计算机工程与设计，2011，32（7）:2381-2384.

[8]王红英.基于Petri网的软件模型验证[D].上海:华东师范大学，2007.

[9]朱文兴，贾磊，丁绪东，等.城市交通网络中的路径优化研究[J].山东大学学报:工学版，2005，35（1）:74-77.

[10]李磊，张冰.GMPLS网络中基于约束的最短路径优先算法[J].电子科技，2007（2）:42-45，50.

The research of shortest path algorithm based on Petri nets

DUAN Ren-hang，ZHAO Pei-si
（College of Electronic Engineering and Automation，Guilin University of Electronic Technology，Guilin 541004，China）

The research of finding the shortest path of traffic.The traditional shortest path algorithm exists the problem of intensive computationally，low efficiency and other issues.In order to find the shortest path in real-time traffic state better，the paper proposes a shortest path search algorithm based on Petri nets on the basis of the research of the shortest path in the previous study.The algorithm can be modeled based on existing traffic roadmap，then modified and simulated on the modeling diagram according to the real-time road traffic conditions.Experimental results show that compared with the traditional algorithm，the new algorithm significantly reduces the amount of calculation that can improve the efficiency of the search for the path.

Petri nets；traffic；the shortest path；expansion tokens；weight of transition；real-time traffic；impact factor

TN99

A

1674－6236（2016）01-0092-04

2015-02-28稿件编号：201502153

段任航（1989—），男，安徽安庆人，硕士研究生。研究方向：智能系统建模。