基于EMD-分形理论的短期电力负荷预测

关学忠，佟 宇，高 哲，聂品磊，皇甫旭

（1．东北石油大学 电气信息工程学院，黑龙江 大庆　163318；2.辽宁大学 轻型产业学院 辽宁 沈阳 110036；3.中海油能源发展股份有限公司安全环保分公司 天津　300000）

基于EMD-分形理论的短期电力负荷预测

关学忠1，佟 宇1，高 哲2，聂品磊3，皇甫旭1

（1．东北石油大学 电气信息工程学院，黑龙江 大庆163318；2.辽宁大学 轻型产业学院 辽宁 沈阳 110036；3.中海油能源发展股份有限公司安全环保分公司 天津300000）

电力负荷预测是电力系统规划的重要组成部分。为了使电力系统安全经济平稳的运行，由此特别需要精确的电力负荷预测方法。为了实现更好负荷预测方法，文中将经验模态分解（EMD）与新兴的电力负荷预测模型分形理论相结合，提出了EMD-分形负荷预测模型。为了证明此方法的有效性，文中将这种新的预测模型跟分形预测模型和BP神经网络预测模型相比较。最终通过仿真算例说明了本文提出的这种新型预测方法精度更高，几乎所有的误差都在2%以下，预测结果更好，可以很好的应用在电力系统负荷预测中。

负荷预测；分形理论；经验模态分解；EMD-分形

电力系统负荷预测是根据电力负荷、经济、社会、气象等的历史数据，探索电力负荷历史数据变化规律对未来负荷的影响，寻求电力负荷与各种相关因素之间的内在联系，从而对未来的电力负荷进行科学的预测[1]。很多新的理论和新的技术不断的更新也推动着负荷预测的发展，很多新的负荷预测的方法层出不穷。文献[2]提出将负荷预测技术分为传统预测方法、现代预测方法、经典预测方法、和组合预测方法。传统的方法总是存在这样那样的弊端。

早在1975年，分形这个专有名词是由曼德勃罗特教授首次提出，分形的早先本身的含义是不规则且支离破碎的物体[3]。以不可微、不光滑的几何图形为主要研究对象是分形几何学所主要研究的内容。自然界本质正是粗糙性和非对称性，这正是分形几何学所主要描绘的内容。

经验模态分解方法（Empirical Mode Decomposition，EMD）是1995年由Huang提出的一种新的信号处理方法[4]。Huang在1999年又将此方法进行了一些改进[5]。EMD分解方法从本质上来说就是对信号进行平稳化的处理，逐级的将分解信号中不同尺度的趋势或者波动，产生出很多具有不同特征尺度的数据序列。这样所得的每一个可以符合条件的序列称作一个本征模函数（intrinsic mode function，IMF）分量。测试结果显示，截止到目前为止，EMD这种方法是提取数据序列趋势或者均值的最好的方法。

1　EMD-分形理论算法原理

1.1经验模态分解法

任何事物的运动、变化、状态都会产生伴随信号，这就意味着信号在现实生活中和自然界当中是普遍存在的。信号本身表示为信息的表现形式和信息的载体，信号分析表示为对信号基本形式的表征和研究。通过对信号的分析从而揭示出信号的结构特征，这种信号分析可以有效地获取、传递和处理信息。电力负荷是具有非线性、周期性、非平稳和非线性的信号。通过长时间的对电力负荷历史数据的分析可知，电力负荷主要是由负荷分量、异常或特殊事件负荷分量、随机负荷分量和天气敏感分量几个方面构成的。电力负荷可分为4类不同的分量，这4种分量受到不同种类因素的干扰影响，因此具有不同种类的变化规律。由此，文中采用将负荷分解，分解之后得到各个负荷分量，再将各个负荷分量分别预测，从而来提高负荷的预测精度。这种方法不是直接对原始的负荷进行直接预测，而是先对历史负荷序列的数据进行处理，之后分别对上述讨论的负荷所包含的其他分量一一进行单独预测。将各个分量预测之后，再将所得的各个分量相加求和，从而来得到最终提高精度的负荷预测结果。结合上述电力系统负荷的一些特点，由此EMD分解来进行电力系统负荷的分解及其预测。

1.2分形插值算法

存在确定的数据集{（xi，yi）:i=0，1，…，M}，这个数据集的吸引子A是内插连续函数F:[x0，xM]→R的图像，下面构造R2上的一个IFS。

IFS{R2；ωm，m=1，2，…，M}，其中ωm是式（1）的仿射变换：

使得bm=0的原因是为了使得与小区间的函数不交叉，这样的结果会令变换后的垂直西那段与原垂直线段相同。

上述结果表示在大区间的左右端点分别映射到子区间的左右端点，所以每个变换都要满足下面的方程：

上式共有4个方程和5个参数，其中存在一个自由参数。ωm的垂直比例因子是dm[7]，这时可以将dm选择为自由变量。令|dm|<1，这样做的目的是使IFS收敛。令K=xM-x0，可得出下面的表达式：

其中IFS的第i个仿射变换可由上述式子得到的参数来确定。IFS的吸引子可通过IFS的各个参数求得。之后经过多次的迭代就可得到一条稳定的插值曲线。传统插值法反映不出两个相邻的信息点之间的局部特征，分形插值可以很好的解决。原来被采样曲线的大部分特征通过插值曲线得到了保留。

电力负荷序列中的那些随机成分经常会对负荷的预测造成很大的影响。于是，文中利用之前讨论过的经验模态分解对原负荷序列的高频随机分量提取出来，然后分别对分量进行建模预测。对原始负荷序列进行分解所得到的趋势分量、随机分量和周期分量后，利用分形预测模型分别对所得到的分量进行预测，然后将各个分量预测的结果进行相加，最后得到最终的预测结果。

综上所述EMD-分形理论算法的实现过程如图1所示。

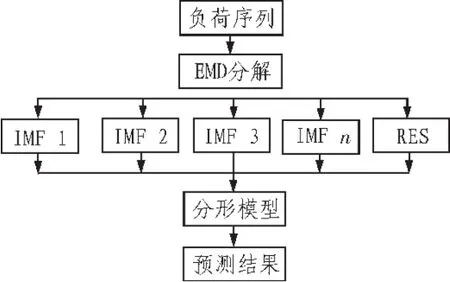
图1　基于EMD-分形短期负荷预测模型Fig.1　Short-term load forecasting based on fractal empirical mode decomposition theory model

2　基于EMD-分形的短期电力系统负荷预测

前面已经重点研究了EMD的分解原理和算法。对比目前常用的短期电力负荷预测方法进行对比研究之后，提出一种基于EMD分形理论的短期电力负荷预测方法。针对负荷序列的随机性、周期性、不平稳等特点，先将负荷序列进行经验模态（EMD）分解，得到IMF分量，再将各个分量分别进行分形预测，最终将各分量预测结果进行相加。

负荷预测的数据是很庞大的，本文只列出北方某地区部分时间的历史负荷数据。首先随机选取我国北方某地区2009 年5月1日至2009年6月份连续50天的整点历史负荷数据作为原始数据。该时段内的负荷曲线如图2中（a）所示。

图2为上述时段负荷序列的EMD分解结果，对图2中的各个图分别进行观察，可以清晰的表现出EMD分解的规律性。

如图 2所示，（a）是原始负荷序列；（b）至（g）为 IMF分量，（h）为余量。分析图2中的各个图像的规律，可从中看出（b）、（c）、（d）所示的IMF分量频率很高，并且不具有明显的周期性，认为它们是负荷序列中的高频分量，也就是负荷序列中的随机分量；（e）和 （f）中的IMF所呈现出一定的周期性，并且幅值很大，所以判定它们为电力系统原负荷序列的周期分量，这种周期分量与气候相关。（g）中的IMF分量具有较强的趋势变化特征，随着时间的增加幅值也慢慢变大，将这个分量划为原负荷序列的趋势分量。最后的（h）曲线是趋势分量的余量。

将上述分析的各个IMF负荷分量分别进行分形预测之后，将它们的各个预测值相加，就能得到最终的预测结果。因为之前所预测的数据量正如由图2中（a）那样较大无法直观的观察出预测结果的好坏，文中随机截取2009年5月28日一天24个点进行观察，并用BP神经网络预测同一天的负荷，从而达到对比的目的。结果图对比如图3。

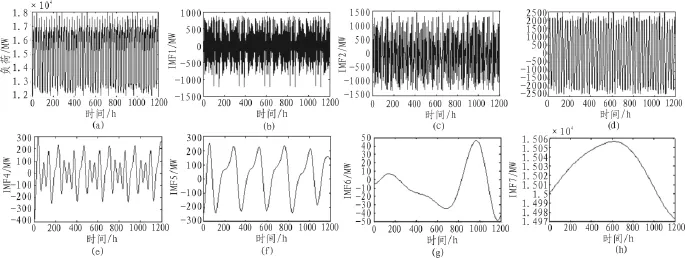
图2　EMD负荷序列分解结果Fig.2　The result of EMD load sequence decomposition

图3　三种预测模型和实际值的比较Fig.3　Comparison of three forecasting models and actual values

3　结　论

图3是3种预测模型的预测值与实际值的对比图。由图3可清晰看到，分形预测和实际值的匹配度要比BP神经网络[8-10]模型要好，基本上和实际值没有多大区别，但是利用EMD-分形模型的预测值实际值的匹配度更高，是三者当中最好的。BP神经网络预测模型的预测结果比其他两种预测模型的预测结果要稍差。它的变化趋势与实际情况的变化趋势在一定程度上还是有差别的。表1是2008年5月28日，3种预测模型的24个小时整点负荷预测结果。从表1中可以看出，分形预测模型的预测误差比较低，比BP神经网络预测模型的预测误差要小，但是也有很多相对误差大于5%。而EMD-分形预测模型要比其他两种模型预测预测误差都要小，是3种模型当中预测误差最小的，几乎所有的误差都在2%以下。算例结果说明，EMD-分形预测模型可以很好的对电力负荷进行预测，这种预测模型有较强的实用性。

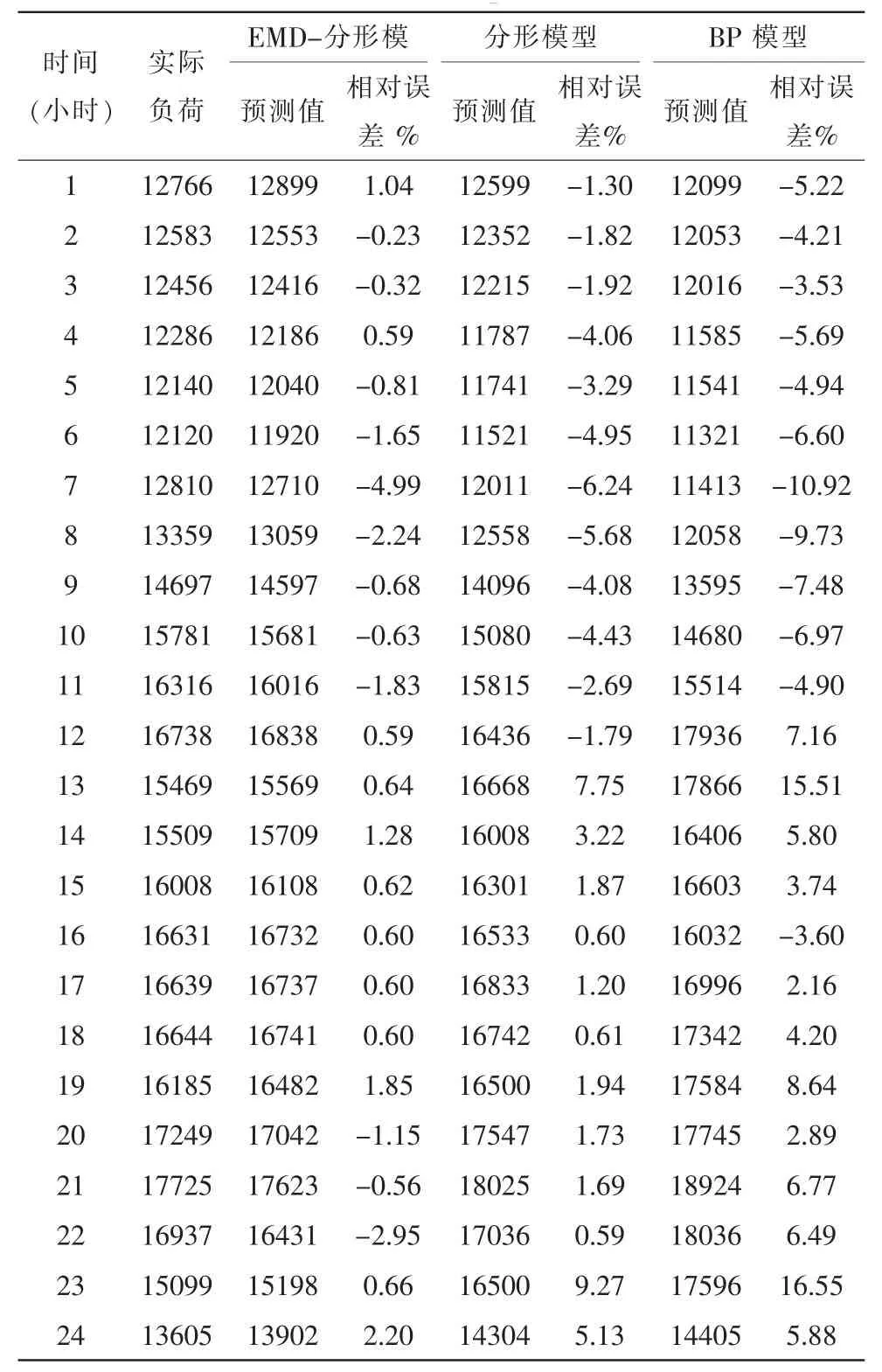
表1　三种模型预测值Tab.1　Three models predicted value

[1]康重庆，夏清，刘梅.电力系统负荷预测[M].北京:中国电力出版社，2007.

[2]Neill-Carrillo E O，Heydt G T，Kostelieh E J.Chaotic phenomena in power Systems:Detection and APPlications. Electric Machines and Power Systems，1999（27）:79-91.

[3]乔艳芬.基于分形理论的电力负荷特性研究及预测[D].北京：华北电力大学（北京）2006.

[4]Huang N.E，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis.Proc.R.Soc.Lond.A.1998.

[5]Huang N E，Shen Z，Long S.R.A new view of nonlinear water waves:the Hilbert spectrum[M].Ann Rev Fluid Mech，1999

[6]Bansley M F.Fractals Everywhere（Second Edition）[M]. Academic Press，1993.

[7]唐立春，李光熹，熊曼丽.基于分形的电力系统负荷预测[J].电力系统及其自动化学报，1999，11（4）:21-24.

[8]金文志.基于改进BP网络的甲烷传感器温度影响试验研究[J].电子设计工程，2015（7）:15-17.

[9]苏宇逍.基于GA的BP神经网络在多目标优化中的应用[J].电子科技，2015（6）:51-53.

[10]李志峰，张二艳.BP神经网络在空气质量评价分级中的探索与应用[J].电子技术与软件工程，2014（5）:43-44.

Short-term power load forecasting based on fractal Empirical Mode Decomposition theory

GUAN Xue-zhong1，TONG Yu1，GAO Zhe2，NIE Pin-lei1，HUANGFU Xu1
（1．College of Electrical and Information Engineering，Northeast Petroleum University，Daqing 163318，China；2．College of Light Industry，Liaoning University，Shenyang 110036，China；3．CNOOC Energy Technology&Services Limited，Tianjin 300000，China）

Power load forecasting is an important part of power system.To make the power system stability，therefore special needs accurate load forecasting method.In this paper，in order to achieve a better load forecasting mode，combine the Empirical Mode Decomposition（EMD）and fractal theory and improve the EMD fractal load forecasting model.In order to prove the effectiveness of this method，the paper use this new forecasting model compared with fractal forecasting model and BP neural network forecasting model.Finally the simulate example illustrates this new forecasting method proposed higher precision and better forecasting.Almost all of the errors are below 2%.The result proved it can be a good application in electric power system load forecasting.

load forecasting；fractal theory；empirical mode decomposition；EMD-fractal

TN0

A

1674－6236（2016）01-0184-03

2015-05-15稿件编号：201505132

国家自然科学基金（61304094）

关学忠（1962—），男，吉林蛟河人，博士，教授。研究方向：智能控制，模糊控制，嵌入式系统。