小波递归最小二乘语音自适应增强

朱宗明，姜占才

（1.中国人民解放军69220部队 新疆 阿克苏　843000；2.青海师范大学 物理系，青海 西宁　810008）

小波递归最小二乘语音自适应增强

朱宗明1，姜占才2

（1.中国人民解放军69220部队 新疆 阿克苏843000；2.青海师范大学 物理系，青海 西宁810008）

针对语音自适应增强的递归最小二乘（RLS）算法必须已知参考信号的约束条件，将小波技术引入RLS算法中，提出了一种语音自适应增强算法-小波递归最小二乘算法（WRLS）。该算法无需参考输入和输入信号的延时量，而是用小波分解、合成技术初估期望信号，以此获得先验误差；再用RLS算法求解滤波器权系数修正量；同时采用"块" 和"符号"技术减少权系数修正的运算量，提高算法的收敛速度。仿真实验表明该算法的增强效果明显优于谱减法和小波增强法。

语音；自适应增强；小波；RLS算法；滤波器权系数

语音增强的目的是从语音的噪声观测中提取尽可能纯净的语音，在军事通信中尤为重要。由于噪声信号的随机性，没有一种方法能达到完全消噪的目的。谱减法及其变形方法以其运算量小、易实时实现、增强效果显著而成为目前的主要方法；小波域语音增强效果显著[1-3]；Wiener滤波是平稳信号时域波形的最小均方误差估计，但短时语音是非平稳的，人们又提出了许多改进或综合算法。语音和加性噪声都是随机信号，都应基于非平稳或宽平稳假设，因此，自适应滤波是语音增强最根本的方法而成为研究热点[4-6]。自适应滤波有最小均方误差（LMS）和递归最小二乘（RLS）两种基本算法[7]，每种基本算法又有FIR和IIR两种类型。将自适应滤波技术应用于语音增强，目前尚存在一些比较困难的问题。文献[5]探讨了LMS类自适应语音增强，文中以基本RLS算法为基础，提出了一种利用小波技术、辅以“块”和“符号”技术的语音自适应增强算法，并对其进行了大量的仿真实验，证明该方法对语音有显著的增强效果。

1　自适应增强的RLS算法原理

语音信号的噪声观测模型一般用式（1）表示：

其中d（n）表示纯净的语音或称为期望信号；v（n）是噪声干扰，这里主要是背景噪声；x（n）是语音的噪声观测。背景噪声一般是宽带的，可用零均值高斯白噪声或该噪声激励一个AR （1）系统来模拟。语音增强的目的是从语音的噪声观测中提取原始语音，可用两种方法实现：一是设法估计噪声，然后从观测信号中减去噪声估计，称为噪声对消法；另一种是对观测信号滤波，直接得到语音的估计，称为滤波法。如图1所示。

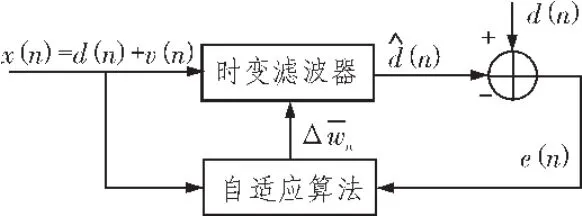
图1　自适应滤波原理Fig.1　Principle of adaptive filtering

自适应滤波的RLS（递归最小二乘）算法是递归修正，并在最小二乘误差意义上最优的滤波算法，其FIR型滤波器是线性相位、因果、稳定的。RLS算法归纳如下。

参数：p为滤波器的阶数；λ为指数加权因子 （遗忘因子）；δ为用于初始化的值。

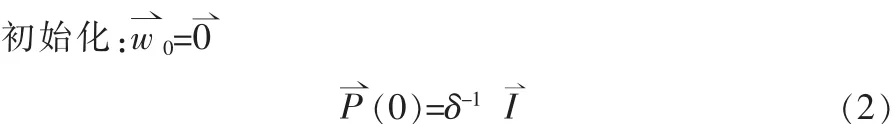
计算公式：对n=1，2，3，…，计算

滤波后信息矢量

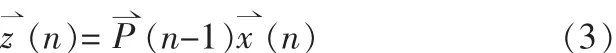
增益矢量

先验误差

修正滤波器

修正逆阵

其中，遗忘因子为0<λ<1的常数，实际取值由实验确定；δ是很小的正数；!I是（p+1）×（p+1）的单位阵；!P（n）是数据矢量的自相关阵的逆阵，即是增益矢量!的共轭转置。

由（5）、（6）两式可知，当先验误差α（n）较小时，表示当前的滤波器权系数在最小二乘意义下接近于最优值，此时只需对滤波器权系数作一小的修正；当α（n）较大时，表示当前滤波器的权系数不能较好地估计d（n），因此要对滤波器作一大的修正。自适应滤波RLS算法的步骤归纳如下：第一步，初始化滤波器和自相关逆阵，即第二步，递归，对n=1，2，…，依次计算式（3）得滤波后信息矢量、计算式（4）得增益矢量!g（n）、计算式（5）得先验误差α（n）、计算式（6）得修正后的滤波器计算式（7）得自相关逆阵

2　小波期望估计原理

小波作为一种有效的时间（空间）/尺度分析工具，为信号分析提供了一种有效的多分辨（多尺度）的表示方法。小波[8]变换能够同时给出信号的时/空域和频域信息，具有良好的时频局部化性能。小波域信号增强能够兼容去噪和保留信号有意义特征。从信号的噪声观测x（n）中求得期望信号的估计d赞（n），可以利用小波分解和小波重构技术，其基本原理和过程是：1）选用适当的小波函数和小波分解层次，对观测数据进行小波分解，分别得到低频和高频分解系数向量{cai}、{cdi}，i= 1，2，…，N，N是选定的分解层数；2）对从第1层到第N层的每一层，采用Stein的无偏似然估计原理，选用一个自适应阈值，对高频系数向量进行软阈值处理。3）根据第N层的低频系数和所有经过处理的高频系数，计算出信号的小波重建，即为期望的估计。小波分解如图2所示。

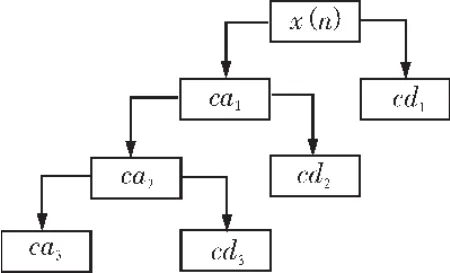
图2　小波分解原理图Fig.2　Principle of wavelet decomposition

3　WRLS语音自适应增强算法

3.1RLS算法语音增强的关键技术

将自适应滤波的RLS算法应用于语音增强时存在一个问题，求先验误差必须先得到参考信号d（n），d（n）就是干净语音，当然是未知的。大量文献给出了两种假设下的情况：1）除了主观测（语音的噪声观测）或称主输入外，还可获得辅观测，它是与主观测中的噪声强相关的随机噪声，该假设在飞行员通信中容易实现；2）将观测信号的适当延时信号作为自适应滤波器的输入，该假设在非语音信号且允许事后处理中容易实现。显然，两种假设在实时语音处理（如通信）中都是难以实现的。

3.2语音自适应增强的WRLS算法

像移动通信这样的语音实时处理，辅观测法和数据延时法是不现实的。欲实现自适应滤波的RLS算法，必须由输入数据即语音的噪声观测x（n）直接获得先验误差α（n），参考信号（期望信号）d（n）虽然未知，但可以先对其进行估计。当然，若果该估计效果理想，即可将该估计直接输出；若果估计效果不佳，则可将该估计作为参考信号，然后用迭代法修正滤波器，使其在最小二乘意义上达到最优。

小波期望估计法虽然具有算法比较简单、去噪效果比较显著等优点，但由于其算法是基于分层高频系数阈值门限处理，其去噪效果仍然是有限的。将小波去噪引入RLS算法中，用于参考信号d（n）的估计，以此获得先验误差α（n），进而对时变滤波器递归修正。这种基于小波和RLS的自适应语音增强算法称为WRLS算法，如图3所示。

图3　WRLS语音自适应增强原理图Fig.3　Principle of WRLS speech adaptive enhancement

为了提高WRLS的运算速度，采取两项技术。一是将先验误差a（n）取“符号”运算；二是滤波器修正时采用“块”技术，即将一帧数据视为块，对块用迭代法得到最优滤波器，而不是在帧的每个样点上进行迭代。

3.3WRLS算法步骤

3.3.1初始化

首先对时变滤波器的权系数和自相关逆阵进行初始化，分别得到初始权系数和是很小的正数，可由试验确定。初始化只在一段语音的最前帧进行，没必要对一段语音的每一帧都进行。

3.3.2修正滤波器

1）求期望信号的估计：对当前的输入帧（语音的噪声观测帧），经小波期望估计器，求出原始语音的估计作为自适应滤波器输出的期望信号；2）求当前帧的滤波后信息矢量：它是初始自相关逆阵与当前帧的乘积，用式（3）计算；3）求增益矢量并取其符号：它与当前输入帧x（n）、当前帧的滤波后信息矢量和遗忘因子λ有关，由式（4）求出，其中λ取0.9；取其符号sign（g），如下式

4）修正自相关逆阵：用式（7）完成对初始自相关逆阵的修正，得到当前帧经一次修正后的自相关逆阵；之后视先验误差α（n），要对阵进行2、3…次的迭代修正，分别得到，直至对当前帧数据，滤波器达到最优为止。

5）求先验误差α（n）：用初始滤波器对当前帧数据进行滤波，得到滤波器输出，由式（5）求a（1），其中和α（1）括号中的1表示第1帧；α（1）经比较器后，决定是否对滤波器进行修正。

6）修正滤波器：若果α（1）大于阈值T，则按式（6）修正滤波器，得到修正后的滤波然后用修正后的滤波器仍然对当前帧进行滤波，求先验误差α（1.2）。

上述过程可以归纳为：对输入的当前帧，先用小波初估期望信号；之后分两路，一路用初始阵求参数，进而修正阵；第二路用初始滤波器对当前帧数据滤波，求先验误差α，与阈值T比较，修正滤波器；两路修正的目标是使滤波器在最小二乘意义上达到最优。若果当前帧是第1帧，则是用真正的初始值，否则，是将前一帧的最优滤波器和最优"P阵作为当前帧的初始值使用，而非对每一帧都初始化。由于语音信号帧与帧之间具有很强的相关性，使得这种初始化方案大大缩短RLS算法的收敛时间，整体上表现为提高了算法速度。

4　算法仿真实验

4.1实验方案

1）直接仿真实验：对同一段语音，在不同的信噪比下，分别用谱减法（ISS）和WRLS法进行仿真实验；在同一信噪比下，用ISS法和WRLS法对不同的语音样本进行滤波。

2）应用仿真实验：将WRLS增强算法植入低速率声码器中，观察比较未经增强环节和经WRLS法增强环节后的语音再经编、解码后的效果。

4.2实验材料（实验用语音样本）

实验用语音取自笔者建立的语音库yyk2.wav，库中语音为8 kHz采样、8 bit量化、线性PCM编码的数字语音。实验时从语音库随机抽取语音段，加入高斯白噪声后形成含噪语音即语音的噪声观测。帧长和帧移都为160点，帧间无重叠。

4.3实验系统（程序）

分别对改进的谱减法和WRLS法编程，以文件名iss.m 和wrls.m存盘；在PC机上仿真实验。

4.4实验结果及其分析

部分实验结果如图4～7所示。图4和图5是同一段语音在信噪比为3 dB时，ISS法和WRLS法的增强结果。实验显示，当信噪比不小于10 dB时，ISS法与WRLS法的增强效果基本相当；但当信噪比小于10 dB时，后者的效果明显优于前者；当信噪比降到3 dB时，前者效果明显欠佳，后者（本文方法）仍然有显著的增强效果。

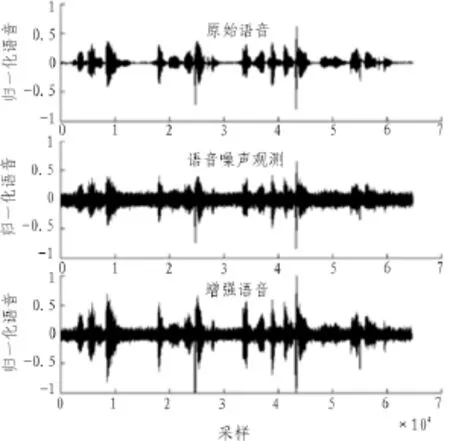
图4　3dB时谱减法语音增强增强Fig.4　Speech enhancement of ISS under 3dB

图6和图7分别是10 dB时，未经增强环节和经WRLS增强环节的语音经过码率为2.4 kbps的混合激励线性预测（MELP）声码器（PC上的软件声码器）后的解码语音。实验显示：未经增强预处理的语音经低速率声码器编码，其解码语音含有明显的噪声（波形和听觉）；经WRLS增强环节再经低速率声码器编码，其解码语音含噪很少、可懂度和自然度明显得到改善。

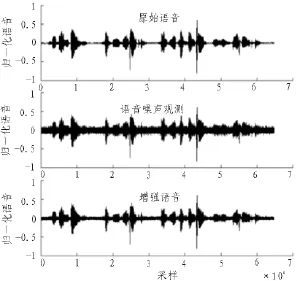
图5　3dB时WRLS法语音增强Fig.5　Speech enhancement of WRLS under 3dB

图6　10dB时未经增强环节的解码语音Fig.6　Decoding speech without enhancement link under 10dB

5　结　论

将自适应滤波RLS算法应用于语音增强时，期望信号（参考信号）的估计是实现有效增强的关键。将小波分析技术引入自适应滤波的RLS算法中，同时采用“块”和“符号”两项技术后得到的WRLS算法，较好地解决了语音自适应增强中滤波器的参考信号未知这一难题，实现了非平稳语音的自适应增强。计算机仿真实验表明，WRLS算法对语音有显著的增强效果，其效果明显优于改进的谱减法，在强噪声环境中（3 dB），其增强效果仍能令人满意。

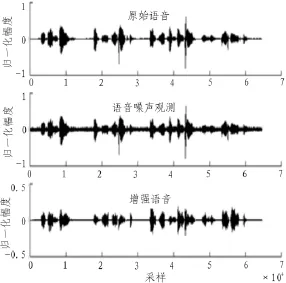
图7　10dB时经WRLS增强环节的解码语音Fig.7　Decoding speech with WRLS enhancement link under 10dB

[1]李野，吴亚锋，刘雪飞.基于感知小波变换的语音增强方法研究[J].计算机应用研究，2009，26（4）:1413-1415.

[2]王振力，张雄伟，刘守生，韩彦明.基于离散小波变换与小波包分解的语音增强算法[J].解放军理工大学学报：自然科学版，2005，6（5）:424-427.

[3]王娜，郑德忠，刘永红.双树复小波包变换语音增强新算法[J].传感技术学报，2009，22（7）:983-987.

[4]柳 林，李辉，戴蓓蓓，等.基于多脉冲激励和卡尔曼滤波的语音增强算法[J].数据采集与处理，2009，24（1）:100-104.

[5]姜占才，孙燕，王得芳.基于谱减和LMS的语音自适应增强[J].计算机工程与应用，2011，47（7）:145-148

[6]姜波，杨军，张尔扬.稀疏自适应Volterra滤波的QRD-RLS算法[J].信号处理，2008，24（4）:595-599.

[7]马国栋，阎树田，贺成柱，等.基于LMS算法与RLS算法自适应滤波及住址分析[J].电子设计工程，2014（6）:43-45

[8]黄达人，刘九芬，黄继武.小波变换域图像水印嵌入对策和算法[J].软件党报，2002（7）:1290-1297.

[9]唐军华，王永刚，刘世辉.一种远场主意信号去噪算法研究与实现，2014（8）:144-146.

Algorithm for speech adaptive enhancement of wavelet recursive least square

ZHU Zong-ming1，JIANG Zhan-cai2
（1.The Chinese People’s Liberation Army 69220 Troops，Akzo 843000，China；2.Physics Department of Qinghai Normal University，Xining 810008，China）

According to recursive least square（RLS）algorithm of speech adaptive enhancement，constraints of the reference signal must be known，the wavelet technique is used in the RLS algorithm，a kind of speech adaptive enhancement algorithm based on wavelet recursive least square（WRLS）is put forward.The algorithm doesn't need reference input and the time delay of the input signal，but desired signal is estimated first by wavelet decomposition，synthesis technology，thus obtaining a priori error；the weight coefficients correction of the filter is obtained adopting RLS algorithm；meanwhile，adopting the technique of "block"and"symbol"reduces the amount of operation of weight coefficients correction，and improves the rate of convergence of the algorithm.Simulation results show that the enhancement effect of the algorithm is obviously superior to the spectral subtraction and wavelet enhancement algorithm.

speech；adaptive enhancement；wavelet；RLS algorithm；weight coefficients of filter

TN912.35

A

1674－6236（2016）01-0069-04

2015-09-01稿件编号：201509005

国家社科基金资助项目（15XYY026）

朱宗明（1985—），男，青海西宁人，助理工程师。研究方向：军事通信和军械保障。