RC高墩位移变形能力计算模型研究

宋晓东

（周口职业技术学院，河南周口　466000）

RC高墩位移变形能力计算模型研究

宋晓东

（周口职业技术学院，河南周口466000）

为研究RC高墩的抗震性能，对4根RC高墩模型进行拟静力试验，观测高墩在循环荷载作用下的破坏形态和变形过程，并基于此提出一个用于评估高墩位移变形能力的计算模型。该模型由墩在一些特征状态时的曲率分布曲线构成。以试验中的3个试件为算例，分别采用JTG/T B02-01—2008《公路桥梁抗震设计细则》中的计算模型、Y K Yeh等人建立的计算模型和本文提出的计算模型进行验算。结果表明：上述3个模型的计算结果与试验结果相比较，最大误差分别为117.04%、36.54%和20.67%，本文提出的计算模型其计算结果与试验结果最相近。

位移变形能力；计算模型；拟静力试验

桥墩的变形能力是衡量其抗震性能的一项重要指标。为保证桥梁抗震设计安全，设计者必须将桥墩设计为有足够的变形能力。墩的变形能力一般分为曲率变形能力和位移变形能力2种。本文对后者进行探讨。墩的位移延性能力可以用其墩顶极限位移来表征。

JTG/T B02-01—2008《公路桥梁抗震设计细则》（简称《细则》）对B类、C类的规则桥墩要求进行容许位移验算［1］。与美国Caltrans规范和欧洲的Eurocode等规范一样，《细则》在评估墩位移延性能力时，采用了简化计算方法，即将墩简化为带塑性铰的悬臂墩计算模型（简称《细则》模型）［2-4］。该模型的优点是计算简便，但简化本身在一定程度上也降低了评估的准确性，墩高越大，计算误差往往也就越大。

目前，对RC高墩抗震性能的理论和试验研究较多，如M J N Priestley等人［5］较系统地研究了墩的位移延性能力与配筋率和轴压比等参数的关系，Lawrence L Dodd等人［6］研究了空心圆柱墩的延性性能，但是对高墩位移延性能力评估方法的研究成果并不多。2002年，Y K Yeh等人［7］提出了曲率分布曲线沿墩高为折线和3次抛物线的组合曲线的计算模型（简称Y K Yeh等人模型）。与《细则》模型相比，该模型有很大进步，但采用该模型的边界条件来确定墩底附近曲率曲线的3次抛物线时，有时得到的是非单调曲线，显然是不合理的。

本文基于对RC高墩模型试验的观测，提出了一个新的评估RC高墩位移变形能力的计算模型（简称本文模型）。以试验中的3个试件为算例，分别采用上述3个计算模型进行验算。结果表明，本文模型的计算结果与试验结果最接近，其适用于RC高墩位移延性能力评估。

1　《细则》模型和Y K Yeh等人模型介绍

1.1《细则》模型

《细则》模型是假设墩在延性变形时，墩底附近存在一个等效塑性铰区域。在墩顶水平集中力作用下，当桥墩达到极限状态时，塑形变形集中在等效塑性铰区域内并均匀分布，而等效塑性铰区域外的墩身则保持弹性，曲率按线性分布。《细则》模型如图1所示。图1中，L为墩高；Lp为等效塑性铰区域长度；φye和φm分别为墩截面的等效屈服曲率和极限曲率。

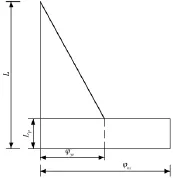
图1　《细则》模型

按图1中的曲率分布模型，即可算出墩的极限墩顶位移Δu：

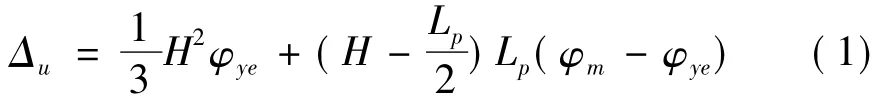
1.2Y K Yeh等人模型

Y K Yeh等人模型假设某墩截面为M-φ曲线，如图2所示。图2中分别为最大弯矩、纵向钢筋首次屈服弯矩和混凝土开裂弯矩；分别为上述各弯矩所对应的截面曲率；（EI）e、（EI）r分别为等效刚度和残余刚度。

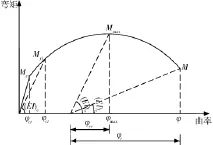
图2　墩截面的M-φ曲线

当墩的最大弯矩处于图2中曲线的上升段时，墩身各截面的曲率可根据弯矩值由M-φ曲线直接查取，从而可计算出墩顶位移。当最大弯矩处于M-φ曲线下降段时，问题就相对变得复杂多了。以图2中M-φ曲线上的M点为例，Y K Yeh等人模型把此时墩的曲率分布曲线用函数表示为：

在塑性变形区域Lp'范围内，曲率分布为3次抛物线，具体形状可根据两端的曲率值和斜率来确定。当M点对应的恰好是墩的极限状态时，则由曲率分布函数通过积分，来算出该墩的墩顶极限位移。Y K Yeh等人模型中墩在各特征状态时的曲率分布曲线如图3所示。

图3　Y K Yeh等人模型

2　本文模型

本文模型是假设某墩的墩底截面M-φ曲线，如图4所示。图4中，Mye是按照面积等效原则，将实际M-φ曲线等效为理想弹塑性曲线时得到的等效屈服弯矩，其在实际的M-φ曲线上所对应的点为为极限状态时的弯矩。

图4　墩截面的M-φ曲线

图5　各特征状态时的墩身曲率分布曲线

本文模型是将墩在某些特征状态时的曲率分布曲线简化成如图5所示的形式。图5中，φm为极限状态时的曲率。

由图5（a）可以看出，墩在首次屈服状态时，墩身的曲率分布曲线为1条双折线，折点在混凝土开裂弯矩Mcr所对应的截面位置，该截面曲率为φcr。由图5（b）可以看出，墩在等效屈服状态时，曲率分布曲线保持为双折线。需要指出的是，为保持与公认等效屈服位移概念的一致性，本模型在计算等效屈服位移时，墩底截面曲率仍采用等效M-φ曲线上等效屈服弯矩Mye点所对应的曲率φye，而并非实际M-φ曲线上点所对应的值。由图5（c）可以看出，墩底截面弯矩达到最大值时，墩身曲率分布曲线线形为三折线。由图5（d）可以看出，当墩的承载能力下降到的80%或纵向钢筋发生断裂时，墩达到极限状态，此时墩身曲率曲线上部为折线，折点为强度峰值状态时，弯矩分别为和截面所处的位置，塑性区域范围内的曲率分布函数φ（x）为2次抛物线，具体形状可由其两端的曲率值和曲线上、下端点斜率等边界条件来确定。

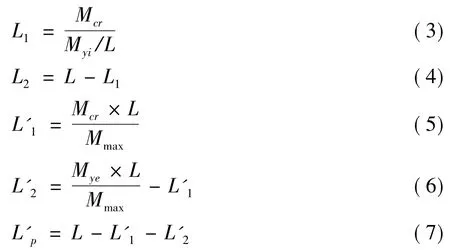
按本文计算模型，可以算出RC高墩在不同特征状态时的墩顶位移值。

1）首次屈服状态时的墩顶位移：

2）等效屈服状态时的墩顶位移：

3）极限状态时的墩顶位移，即墩的位移延性能力值：

式中：φ（x）为墩的曲率分布函数。

3　RC高墩模型拟静力试验

同济大学土木工程防灾国家重点实验室对4根RC箱型截面高墩模型进行了拟静力试验，以研究其延性抗震性能［8］。试件主要设计参数如表1所示，其中1～3号试件采用箱型墩截面，4号试件采用哑铃型截面。

试验时，试件测点布置为：在墩顶安装水平位移传感器，在主筋上粘贴应变片以测量主筋应变，在墩底附近安装钢纤式位移传感器以测量墩底附近变形曲率。

加载装置采用德国schenck公司生产的PLZ630x型电液伺服作动器，其最大加载能力为630 kN，行程为250 mm。

试验过程中，观察发现各试件的破坏过程和特征基本相似，均是在墩顶位移达到约20 mm时，在墩身下半部首次发现细小水平裂缝，且多条裂缝几乎同时出现，间隔约15～20 cm，由高向低渐次加密。随着加载等级加大，裂缝增多并逐渐发育，到加载后期，裂缝集中在墩脚塑性铰区域，继而墩脚混凝土保护层脱落，纵向钢筋发生屈曲且最后断裂。

4　试验结果与理论计算值的对比分析

试验过程中，发现1号试件有制作缺陷，所以本文只采用其他3个试件的结果。试件位移变形能力实测值和采用上述3种计算模型算出的评估值如表2所示。

表1　箱形墩试件主要设计参数

表2　延性变形能力的实测值和理论计算值mm

从表2可以看出，3个计算模型中，本文模型的计算结果与实测值最为接近，其算出的极限位移与实测值的最大误差是20.7%（3号墩），而《细则》模型与实测值的最大误差是117.04%（2号墩），Y K Yeh等人模型与实测值的计算误差为36.54%（2号墩）。

5　结论

1）本文模型能够较准确地评估RC高墩的位移变形能力，可用于高墩抗震设计。

2）《细则》模型会高估RC高墩的位移变形能力，偏于不安全，故其主要适用于高度较小的规则桥墩。

3）与《细则》模型相比，Y K Yeh等人模型在计算RC高墩的位移变形能力时准确性要好一些，但仍存在较大误差。

4）RC高墩墩顶位移较大时，墩身下半部较大范围内均有水平裂缝出现，墩身曲率在这些地方有较大变化。由于墩的高度较大，墩顶位移对曲率变化比较敏感。所以，《细则》模型将墩身曲率简化为线性是不合适的，这也是其计算结果误差较大的主要原因。

［1］重庆交通科研设计院.JTG/T B02-01—2008公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［2］ California Department of Transportation.Seismic Design Criteria，Version1.2［S］.［S.l.］：California Department of Transportation，2001.

［3］ California Department of Transportation.Bridge Design Specifications［S］.［S.l.］：California Department of Transportation，2001.

［4］European committee for standardizator.Design Provisions for EarthquakeResistanc of Structures，Eurocode 8，Part 2：Bridges［S］.Brussels：Europeancommitteefor standardizator，1994.

［5］M J N PRIESTLEY，R PARK.Strength and Ductility of Concrete Bridge Columns under Seismic Loading［J］.ACI Structural Journal，1987，84（1）：61-76.

［6］ LAWRENCE L DODD，NIGEL COOKE.Capacity of Circular Bridge Columns Subjected on Base Excitation［J］.ACI Structural Journal，2000，97（2）：297-307.

［7］Y K YEH，Y L MO，C Y YANG.Seismic Performance of Rectangular Hollow Bridge Columns［J］.ASCE Journal of Structural Engineering，2002，128（1）：60-68.

［8］宋晓东.桥梁高墩延性抗震性能的理论与试验研究［D］.上海：同济大学桥梁系，2005.

Study on RC High Pier Displacement&Deformation Capacity Calculation Model

SONG Xiaodong

In order to study the seismic performance of RC high piers，this paper carries out pseudostatic testing to 4 pieces of RC high pier models，in order to observe destruction form and deformation process of high pier under cyclic loading，and suggests a calculation model to evaluate high pier displacement and deformation capacity.This model consists of Curvature distribution curve at some featured status.This paper takes 3 test samples in test as example，applying calculation models given in TJT/T B02-01-2008"Anti-seismic design details for road bridges"，set up by Y K Yeh，etc.，and suggested in this essay，respectively，for verification.Results show that，compared with the test results，the maximum tolerance of the calculation results of the three models mentioned above were respectively 117.04%，36.54%and 20.67%.Calculation model suggested in this essay has the closest result.

displacement and deformation capacity；calculation model；pseudo-static testing

1009-6477（2016）04-0072-04

U443.22

A

10.13607/j.cnki.gljt.2016.04.016

2016-03-23

宋晓东（1973-），男，黑龙江省哈尔滨市人，博士，副教授。