空心薄壁高墩横隔板设置条件中线弹性经验公式研究
陈发强,陈 记,孙晓立
(广东省南粤交通投资建设有限公司,广州 510100)
空心薄壁高墩横隔板设置条件中线弹性经验公式研究
陈发强,陈记,孙晓立
(广东省南粤交通投资建设有限公司,广州510100)
从局部稳定角度出发,考虑空心薄壁高墩截面尺寸、墩高、初始缺陷等因素,利用ANSYS软件建立实体模型并对其进行有限元数值分析。拟合空心薄壁高墩局部稳定容许宽厚比修正经验公式,并将该经验公式计算结果作为是否需要设置横隔板的依据。
局部稳定;空心薄壁高墩;容许宽厚比;有限元分析;修正经验公式
山区公路建设经常要跨越河流、峡谷等复杂地形,因地势陡峭,相对落差较大,高桥墩的修建日益增多,墩高超过40 m的高墩桥梁占我国山区桥梁总数的40%以上。
常用高墩施工工法要求结构尽量简洁、整齐,避免局部突出,而横隔板的设置对施工工期和造价的影响较为突出,因此取消横隔板已成为迫切的现实需求。
陈辉等[1-4]对空心薄壁高墩横隔板进行了研究。李国豪[5]给出了5种端部支撑条件下板的弹性翘曲临界应力解析解。彭元诚等[4]的理论是基于限制壁板边长与壁厚的比值使局部屈曲应力高于材料极限强度的想法,将四边简支板的弹性翘曲临界应力解析解变换,并考虑一定的安全系数,得到箱型薄壁截面容许宽厚比解析解:
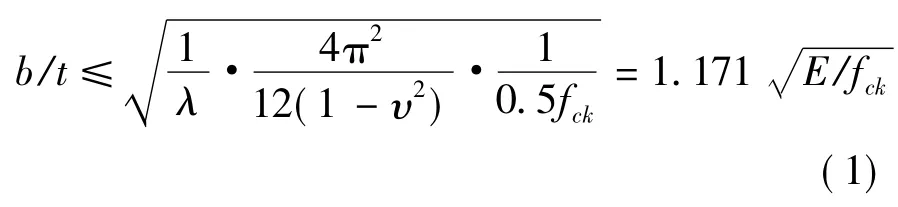
式中:b为箱型截面宽度(约定长边尺寸为宽度,短边尺寸为高度);t为截面厚度;E为弹性模量;fck为混凝土轴心抗压强度标准值;λ为稳定安全系数,根据试验统计确定,粗略取4;υ为泊松比,取0.2。
目前箱型薄壁截面容许宽厚比解析解这一研究成果主要是针对个例的数值分析、试验研究和特定边界条件,没有考虑截面尺寸、墩高、初始缺陷等因素对空心薄壁高墩局部稳定的影响,故无法推广应用于其它的结构设计,且国内外规范中也没有明确的空心薄壁墩设置的计算分析方法。而实际工程中,在空心薄壁高墩中设置横隔板比较随意,往往根据经验来设置。
现有研究表明,横隔板的主要作用是限制墩壁的横向变形,推迟空心薄壁高墩局部失稳的发生[6-7]。所以,通过限制截面宽(b)厚(t)比b/t,便可保证高墩局部失稳在其整体失稳后发生,从而可不必设置横隔板。显然,空心薄壁桥墩的宽厚比b/t必然存在一个临界值,定义为容许宽厚比,当实际宽厚比大于这个临界值时,第1阶线弹性失稳为局部失稳;当实际宽厚比小于临界值时,第1阶线弹性失稳为整体失稳。
本文选取最普遍的空心薄壁墩截面形式作为研究对象,其截面尺寸如图1所示。图1中,B为截面外轮廓宽度(约定长边尺寸为宽度,短边尺寸为高度);A为截面外轮廓高度;H为墩高。
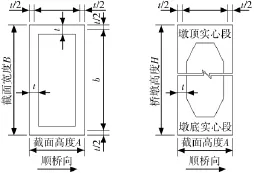
图1 空心薄壁墩尺寸示意
以公式(1)为基础,假定影响容许宽厚比的几种因素相互独立、互不影响,则综合影响应为各个影响系数的乘积,其计算公式为:

式中:K(H/B)为墩高H与截面外轮廓宽度B的比值对局部稳定容许宽厚比的影响系数,拟合计算时计入初始缺陷的影响;K(B/A)为截面外轮廓宽度B与截面外轮廓高度A的比值对局部稳定容许宽厚比的影响系数,拟合计算时计入初始缺陷的影响。
连续刚构桥的稳定性由最大悬臂状态控制[8-10],故容许宽厚比经验公式的推导过程仅需计算最大悬臂状态。
本文计算选取某连续刚构桥主墩进行计算。该桥跨径布置为85 m+155 m+85 m,桥宽12.25 m,主墩采用C40混凝土单肢空心箱型断面,桥墩截面尺寸为6.0 m×5.0 m。
计算荷载考虑结构自重、风荷载、挂篮坠落、主梁两侧重量不平衡、施工荷载等,日照温差及垂直度施工误差引起的桥墩偏位作为初始缺陷。
1 桥墩高宽比对容许宽厚比的影响
根据国内现有高墩桥梁的统计资料,空心薄壁桥墩墩高一般为40~120 m,外轮廓高宽比H/B一般为5~20。
采用控制变量法对某连续刚构桥桥墩高宽比进行分析时,固定B值不变,令A=B,且改变墩高H值,并维持上部传递的荷载不变,通过试算求得第1阶线弹性失稳为局部失稳时的壁厚t0,如表1所示。

表1 第1阶线弹性失稳为局部失稳对应的截面临界壁厚t0(A=B=6 m)
对表1数据进行拟合,得到如下(b/t)0~H关系曲线方程式:
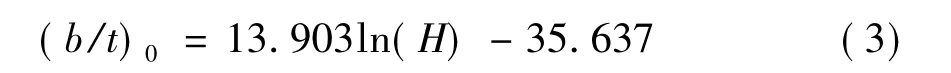
基于表1数据,拟合得到临界宽厚比与墩的关系曲线,如图2所示。
将式(1)计算得到的宽厚比定义为临界宽厚比(b/t)0,将式(3)等于式(1)时的墩高定义为临界墩高,则C40混凝土临界墩高H0=243.8 m,临界高宽比(H/B)0=40.63,临界宽厚比(b/t)0=40.78。基于表1数据,拟合得到容许宽厚比与桥墩高宽比的对应关系曲线,如图3所示。

图2 临界宽厚比与墩高的关系曲线

图3 C40混凝土空心薄壁桥墩容许宽厚比与墩高宽比的对应关系
桥墩高宽比对容许宽厚比的影响系数为:

2 截面宽高比对容许宽厚比的影响
空心薄壁高墩横桥向尺寸(截面宽度)≥顺桥向尺寸(截面高度),即B≥A时,B/A比值一般为1.0~3.0。
采用控制变量法对某连续刚构桥桥墩高宽比进行分析时,固定墩高H,B取实际尺寸,改变A值,并维持上部传递的荷载不变,通过试算求得第1阶线弹性失稳为局部失稳时的临界壁厚,如表2所示。

表2 第1阶线弹性失稳为局部失稳时对应的临界壁厚t0(B=6 m,A≤B)
基于表2数据,拟合3条关系曲线,如图4所示。
图4中,对应墩高为40、80、120 m的截面宽高比与截面容许宽厚比拟合关系曲线如下。

图4 截面宽高比与容许宽厚比的关系曲线
图4中的3条曲线中,H=120 m虽与基准墩高还有差距,但为简化计算,采用H=120 m的曲线作为K(B/A),即
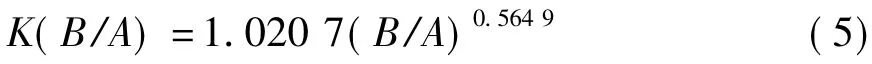
将式(4)、(5)代入式(2),可得到容许宽厚比的线弹性修正公式:
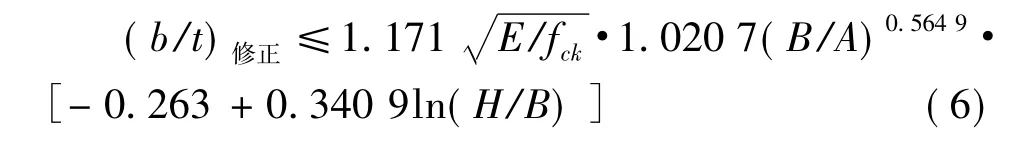
3 ANSYS实体模型计算验证
利用ANSYS软件,采用实体单元或壳单元建立分析模型。通过对实体模型中不同桥墩高宽比、截面宽高比进行分析,模拟得到其局部失稳下的容许宽厚比(t/m),即ANSYS实体模型计算值。第1阶弹性屈曲计算模型如图5所示。

图5 第1阶弹性屈曲计算模型
笔者选取武深、汕昆、汕湛等3条高速公路中连续刚构桥、结构连续T梁桥和桥面连续小箱梁桥的24组高墩,将容许宽厚比线弹性修正公式计算值与ANSYS实体模型计算值进行比较,结果如表 3所示。
由表3可知,线弹性修正经验公式与ANSYS实体模型容许壁厚的最大绝对误差为3 cm,对于混凝土结构而言其计算精度已经很高,证明公式(2)的计算假定成立。另外,以连续刚构桥主墩计算数据为基础拟合得到的线弹性修正经验公式(5)同样适用于连续刚构桥过渡墩、结构连续T梁桥和小箱梁桥等各类矩形空心薄壁桥墩的横隔板计算。

表3 ANSYS与线弹性修正经验公式的线弹性临界宽厚比计算值比较
4 结束语
本文从稳定角度出发,提出空心薄壁桥墩的整体失稳先于局部失稳发生则不需再设置横隔板。利用ANSYS软件建立了实体模型并对其进行了有限元数值分析,拟合了容许宽厚比线弹性经验公式。该公式考虑了桥墩高度、截面尺寸、初始缺陷等因素的影响,适用范围广,计算精度高,可用于实际工程设计。
[1] 陈辉.空心薄壁高墩结构优化设计[D].哈尔滨:哈尔滨工业大学,2011.
[2] 何黎.薄壁空心桥墩非线性失稳研究[D].重庆:重庆交通大学,2011.
[3]管敏鑫.空心桥墩墩壁的局部稳定[J].桥梁建设,1988(3):64-67.
[4]彭元诚,方秦汉,李黎.超高墩连续刚构桥设计中的关键技术[J].桥梁建设,2006(4):30-35.
[5] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1996.
[6]冯磊.基于屈曲理论的典型结构强度分析[D].西安:长安大学,2005.
[7]田志杰.超宽圆端形薄壁空心桥墩稳定性研究[D].兰州:兰州交通大学,2013.
[8]何波,郭小川,朱宏平,等.大跨度薄壁墩连续刚构桥稳定性分析[J].公路交通科技,2006,23(12):62-66.
[9]王海良,金城.黄河特大桥高墩稳定性分析[J].公路,2012(4):124-127.
[10]李黎,廖萍,龙晓鸿,等.薄壁高墩大跨度连续刚构桥的非线性稳定分析[J].工程力学,2006,23(5):119-124.
Study on Elastic Empirical Formula for Setting Conditional Center Line of Transverse Diaphragm on Hollow Thin-Walled High Pier
CHEN Faqiang,CHEN Ji,SUN Xiaoli
In view of local stability,this paper takes consideration of sectional dimension,pier height,initial defect,etc.of hollow thin-walled high pier,and uses ANSYS software to setup an entity model for finite element numerical analysis.This paper obtained a modified empirical equation for stably allowed local width-thickness ratio of hollow thin-walled high pier.The calculation result is used as basis for whether a transverse diaphragm is needed.
local stability;hollow thin-walled high pier;allowance width-thickness ratio;finite element analysis;modified empirical formula
1009-6477(2016)04-0068-04
U443.22
A
10.13607/j.cnki.gljt.2016.04.015
广东省交通运输厅科技项目(2015-02-025)
2016-02-25
陈发强(1981-),男,湖北省随州市人,本科,工程师。

