封闭式独立路权下公交车路阻函数研究

王有为，张子阳

（林同棪国际工程咨询（中国）有限公司，重庆　401121）

封闭式独立路权下公交车路阻函数研究

王有为，张子阳

（林同棪国际工程咨询（中国）有限公司，重庆401121）

对公交车辆行驶过程进行分析，指出在封闭式独立路权下，公交车行驶过程中存在站台停靠、出站等候、交叉口3方面的延误。利用排队论、间隙理论、信号控制理论，构建公交车行驶过程中的延误模型，提出封闭式独立路权下公交车的路阻函数。

公交优先；独立路权；路阻函数

随着城市交通拥堵的加剧，“公交优先”已成为多数城市解决交通问题的首要选择。从“公交优先”的内涵看，“路权优先”是“公交优先”政策实施的具体表现，而公交车在不同路权下的行驶特点不尽相同，故用传统的路阻函数来表示公交车的行驶特点已不再合适［1］。另外，采用“公交优先”理念时，也要求针对公交车的运行特点，分析其在路段上行驶的运行规律，构建合适的路阻函数。而传统路阻函数忽略了公交车与其他车辆运行特征的不同，不能真实反映车辆之间因差异存在而产生的干扰现象。为此，本文对“公交优先”原则下公交车的路阻函数进行研究。

1　封闭式独立路权下公交车行驶过程分析

封闭式独立路权指有封闭式公交专用路或封闭式公交专用车道的路段，公交车在该类路段上行驶时处于相对独立的系统中，不会受到其他社会车辆干扰［2］。此时，公交车行驶过程中的延误主要分为3部分，即站点停靠延误、公交车出站等候延误及交叉口信号控制延误。

1.1公交车停靠过程分析

公交车辆区别于其他类型车辆的一个重要特点就是公交车要在其运行线路的停靠站点停靠，是公交运营系统中不可缺少的环节［3］。而正是由于存在“停靠”这一行为，也使得其运行过程中有独特的运行特点，即公交车停靠的同时既产生了空间上的移动，也产生了时间损耗。

公交车停靠过程中产生的空间上的移动可以分为纵向和横向2部分：纵向移动是公交车在前进方向上的移动过程；横向移动是在垂直道路前进方向上公交车位置的变化过程。

对于时间损耗而言，理论上公交车从进站到离站，整个过程一般可分为5部分：减速进入停靠站—打开车门—乘客上下车—关闭车门—加速离开停靠站［4］。但实际上公交车停靠车站的过程比较复杂，会受到多种因素的影响，可能会因个别乘客乘车而产生2次停靠现象，或因公交车之间相互干扰而产生冲突延误，也可能因停靠车辆过多而产生进站排队等现象。

公交车停靠过程消耗的总时间计算公式为：

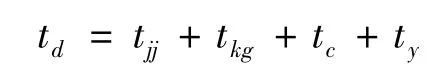
式中：td为公交车停靠过程消耗的总时间为公交车进出站减速、加速过程的延误时间为公交车开门、关门过程消耗的时间，s；tc为公交车在站点供乘客上下车的时间，s；ty为公交车因其他原因产生的总延误时间，s。

本文假设公交车驾驶员职业行为规范、公交车乘客行为规范，不考虑公交车因某些原因产生的延误。

1.2交叉口延误分析

1.2.1交叉口公交优先信号控制

公交优先信号控制是以公交车辆运行效益最优为基础进行的交通信号配时。在公交优先信号控制的交叉口，与其他车辆相比公交车拥有优先通行权，公交车辆到达交叉口时，智能信号控制系统发出公交车拥有优先的通行信号，可保证公交车辆快速通过交叉口而不产生延误。

1.2.2交叉口常规信号控制

在常规信号控制的交叉口，因信号控制原因，不同流向的车辆按信号灯指示依次拥有通行权。因此，车辆通过交叉口时会因信号控制产生延误。对于公交车来说，在交叉口处的延误无疑会增加其在整个行驶过程中的行程时间，对整个公交系统的运行会产生影响，故需要进行研究。

2　公交站点停靠延误分析

每个公交站点都有1个或1个以上的停靠泊位供公交车进站停靠使用，且每个停靠泊位之间相互独立，不受其他泊位的干扰，故可以认为公交站点的停靠泊位是一个排队系统的服务台；而公交车在进站停靠前，均需变换至邻近站点的车道，再依次驶入站点停靠，故可认为在这个过程中公交车随机到达并形成了单路排队，即公交车在公交站点依次排队停靠的过程构成了“单路排队多通道服务的M/M/c系统”，如图1所示。

公交车站点的M/M/c服务系统指当公交站点无公交车停靠或停靠公交车数量小于站点停靠泊位数时，到达的公交车按照先后顺序进站停靠；当公交站点停靠泊位被全部利用时，到达公交车在站点下游排队等待，当站点出现了空闲泊位后，排队等待的公交车按照先到先服务的原则进站停靠，接受服务。

图1　M/M/c排队系统示意

在公交站点，若公交车数n不超过c，则公交站点服务率为nμ( n≤c)；若公交车数超过c，则M/M/c系统不能对所有车辆提供服务，超过泊位数的后续公交车必须排队等待，直到出现空余泊位时才能进站，此时公交站点的服务率仍为cμ。

M/M/c系统状态转移［5］如图2所示。

图2　M/M/c排队系统状态转移关系示意

由图2可得

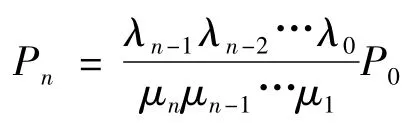
式中：Pn为n辆公交车排队的概率；P0为公交站点无公交车停靠的概率。

当n≤c时：

当n＞c时：

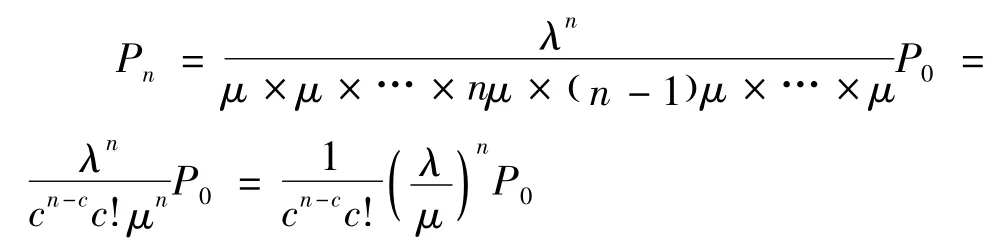
对于公交站点来说，其状态分为2种：无公交车停靠和有公交车停靠。因公交站点停靠泊位对进站的公交车提供服务，故所有公交车在公交站点应有2种状态：一是公交车直接进站停车，无需等待，此时停靠公交车数应≤公交站点的泊位数，即n≤c；二是公交站点所有泊位被占用，公交车需排队等候才能进站停靠，此时排队等候进站停靠的公交车数＞公交站点的泊位数，即n＞c，有n-c辆公交车在站外排队等候。

因此，公交车在公交站点因停靠产生的延误时间，分别与不同状态出现的概率相关。公交车进站无需排队的概率为：

公交站点无公交车停靠、公交车进站无需排队及公交车排队等待进站的概率和为1，即

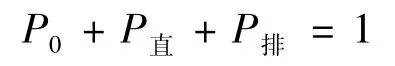
对于整个公交站点来说，所有停靠公交车的平均停靠延误时间应为：

式中：T延为公交车在公交站点的平均延误时间，s；T直为直接进站停靠公交车的平均停靠延误时间，s；T排为排队进站停靠公交车的平均停靠延误时间，s；P直为公交车直接进站停靠的概率；P排为公交车排队进站停靠的概率。

3　公交车停靠延误时间计算模型

受所在路段条件和功能设计限制，公交站点设置主要分为2种类型：直停式和港湾式。不同类型的公交站点，公交车在进站停靠过程中产生的延误也不同。

3.1直停式公交站点公交车停靠延误模型

在直停式公交站点，公交车停靠延误时间主要包括减速进站、加速出站时间，开关门时间及乘客上下车时间。

由于减速进站、加速出站过程产生的延误较小，本文计算忽略这部分微小延误。另外，公交车开关车门时间与公交车车门系统的固有属性有关，公交车开关门的总时间一般在3～5 s，是一个相对较短的过程，本文取平均值4 s。

公交车上下客时间tc（s）与多方面因素有关，这些因素主要包括公交车车门数、售票形式、客流量、是否排队、是否有台阶、乘客人均上下车时间等。徐康明等［6］采用如下公式来计算公交车上下客时间：

式中：p为上下乘客总人数；a为最繁忙车门上下车人数占总上下车人数的比例；t'为人均上下车时间，s，一般为2 s。

在直停式公交站点，公交车停靠延误时间为：

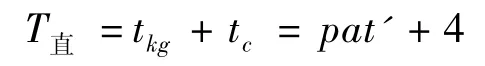
经过公交站点的公交车平均延误时间，既包括公交车在站点停靠产生的延误，也包括公交车进站排队过程中所产生的等待时间。根据第2节对M/M/c排队系统分析得出的结论，可以得到公交车在直停式公交站点的总延误时间为：

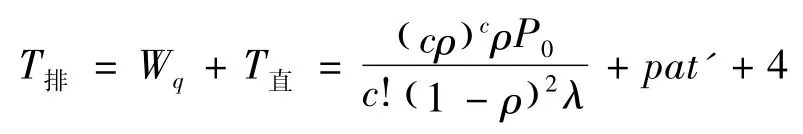
式中：Wq为公交车排队等待时间，s。

直停式公交站点公交车的停靠延误模型为：

3.2港湾式公交站点公交车停靠延误模型

由于港湾式公交站点在车行道外侧，不占用车行道道路资源，使得公交车在停靠过程中减少了对机动车道中行驶车辆的干扰，但这种设计也在一定程度上增加了公交车在站点处停靠的时间延误。公交车在驶出港湾的过程中，必须寻找紧邻机动车道上机动车之间的可插间隙，只有当间隙时长足以满足公交车汇入机动车道时公交车才能驶出公交站点。

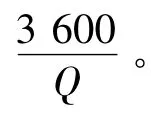
间隙理论认为车头时距的分布符合负指数分布。当ht≥τ时，车头时距能够满足公交车汇入邻近机动车的最小间隔，港湾内的公交车无需等待便可以直接汇入邻近机动车道；当ht＜τ时，港湾内的公交车需要等待可插间隙以汇入邻近机动车道。车头时距的概率分布模型为：

根据间隙理论，假设公交车需要等待的间隙数量为nd，之后会出现一个非阻塞，公交车能汇入邻近车道。公交车的平均延误时间为d：

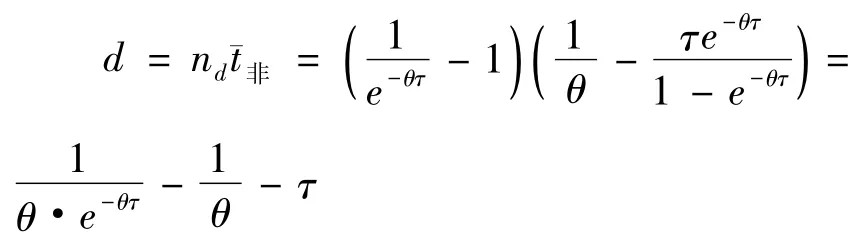
综上所述，港湾式公交站点公交车停靠延误为：

4　交叉口处公交车延误

假设公交车平均到达率在1个周期内保持不变，但在不同周期其到达率有所不同，且在一定时间内到达和离开交叉口的车辆始终保持平衡，这样便可以用稳态理论来计算信号交叉口处车辆延误时间。可将延误分为如下2部分：车辆均衡相位延误和随机延误［8］。

4.1均衡相位延误

当交叉口处于非饱和状态下，即交叉口进口道的通行能力大于进口道的交通需求时，在1个信号周期内，到达交叉口的车辆能完全离开交叉口而不会产生2次等待。

假设信号交叉口的周期时长为C（s），某一相位的有效绿灯时间为g（s），有效红灯时长为r（s）。公交车到达交叉口的平均到达率为λ（辆/s），车辆离开交叉口的平均饱和流率为S（辆/s）。

假设第m辆车为延误最小且不为零的车辆，则第m+1辆车的延误应等于零。由于1个周期内交叉口进口道全部车辆的停车总延误为DL，且di是一个等差数列，则

式中：DL为交叉口进口道全部撤离的停车总延误，s。

故平均车辆延误dL为：

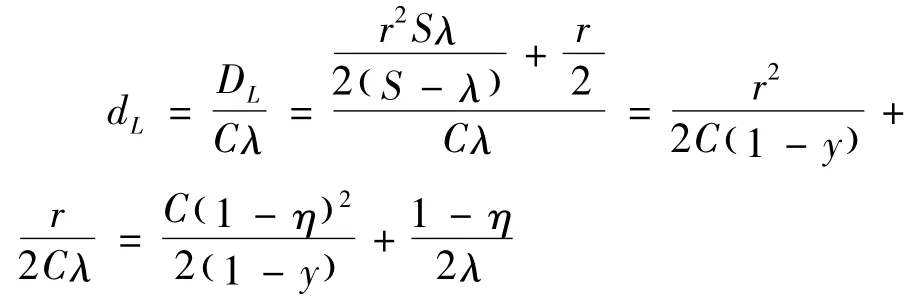
4.2随机延误

随机延误可以用排队论［5］中的公式来表示，假设在到达车辆与信号之间插入一个想象的排队系统，该排队系统的到达率服从均值为λ的泊松分布，该排队系统的驶出率为常数ρ，这样该排队系统中每辆车的平均延误为：

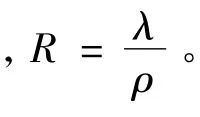
综上所述，公交车在信号控制交叉口其停车延误D应等于均衡延误和随机延误的和，即：

5　公交车路阻函数

封闭式独立路权下，公交车行驶延误可分为如下3部分：站点停靠延误、驶出站点汇入邻近车道延误和交叉口信号控制延误。在前文的分析中，将站点停靠延误和驶出站点汇入邻近车道延误合并为站点延误T延，交叉口信号控制延误为D。

对于公交车的路阻函数来说，除上述延误时间外，公交车自由行驶时间还包括其按照安全行驶速度行驶时所消耗的时间t0。因此，封闭式独立路权下公交车的自由行驶时间为：

公交车的路阻函数为：

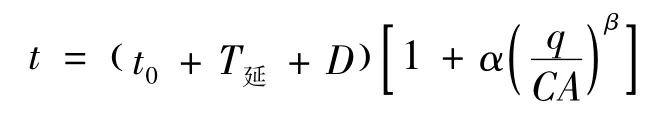
式中：α、β均为美国公路局路阻函数（BPR函数）参数；CA为公交车道通行能力。

6　算例分析

作如下假设，有一个长1 km的公交专用路段，公交车平均行驶速度为40 km/h；该路段上有一个直停式公交站点，其有停靠泊位2个；经过该公交站点的公交线路有6条，高峰时段每条公交线路发车间隔均为5 min，在该站点上下公交车的乘客分别为800和1 400人/h；在公交专用道上行驶但不在该站点停靠的公交车数为900辆/h；每条线路上下车乘客数相同，乘客均匀到达公交站点。

根据前文公式，可以计算并得到公交车在该路段上的行程时间为：

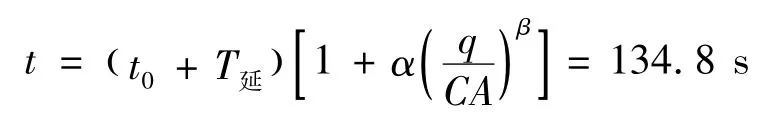
而利用BPR函数计算得到公交车在该路段的行程时间为：t=91.1 s。可以看出，利用BPR函数计算的结果与本文所建模型计算结果差异较大，本文模型更符合实际。

另外，本文还分别改变公交车的车间隔和下客人数来验证本文所建模型的准确性。公交车发车间隔分别为3、4、5 min，下客人数分别为1 400、1 700、2 000人/h时，本文模型及BPR函数模型计算结果见表1、表2。

从表1可以看出，随着进站停靠的公交车增多，公交车平均行程时间变大，与BPR函数计算结果和实际情况相符。

从表2可以看出，随着上下车乘客的增加，公交车在站点处停靠时间和行程时间也随之增加，其与实际状况相符。而BPR函数计算结果则不能反映站点客流变化对公交车行程时间的影响，故本文所建的模型更符合实际。

表1　公交车发车间隔不同时路段行程时间

表2　公交车下车乘客不同时路段行程时间

7　结束语

本文对封闭式独立路权下公交车的运行过程进行了分析。分析证明，公交车运行过程中，除了在路段上正常行驶所消耗的时间外，还存在站点停靠、驶出站点汇入机动车道等待、交叉口信号控制等3方面的延误。另外，本文以排队论为基础，分析了公交站点服务公交车进出站的过程，得到了公交车在直停式公交站点停靠所产生的延误，并根据间隙理论分析了港湾式公交站点公交车在出站过程中需要寻找可汇入间隙而产生的平均等待延误，且还利用稳态理论和排队论相关知识分析了公交车在信号控制交叉口产生的延误，建立了公交车的路阻函数，并通过算例分析，证明了本文所建模型的正确性。

［1］张子阳.公交优先规则下的路阻函数研究［D］.重庆：重庆交通大学，2015.

［2］ 张泉，黄富民，杨涛，等.公交优先［M］.北京：中国建筑工业出版社，2010.

［3］宋路娟.基本路段路内公交停靠站通行能力模型［D］.西安：长安大学，2010.

［4］过秀成，严亚丹.地面公共交通运行可靠性分析与调度控制［M］.南京：东南大学出版社，2013.

［5］ 《运筹学》教材编写组.运筹学［M］.北京：清华大学出版社，2008.

［6］徐康明，解建华，冯浚.快速公交车站运营模式的优势与效益分析［J］.城市交通，2006，11（4）：29-33.

［7］ 王殿海.交通流理论［M］.北京：人民交通出版社，2002.

［8］ 吴兵，李晔.交通管理与控制［M］.北京：人民交通出版社，2008.

Research of Road Resistance Function of Bus Under Closed Independent Right of Way

WANG Youwei，ZHANG Ziyang

Based on analysis on driving path of buses，this paper indicates 3 aspects of delay of bus during in-station parking，exit-station waiting，and intersection with closed independent right of way.This paper sets up a delay model for bus with the help of queuing theory，gap theory，signal control theory，and suggests the road resistance function of buses with closed independent right of way.

Bus priority；independent right of way；road resistance function

1009-6477（2016）04-0134-06

U491.1+4

A

10.13607/j.cnki.gljt.2016.04.030

重庆市科委基金项目（cstc2015jcsf30003）

2016-04-11

王有为（1983-），男，江苏省南京市人，硕士，工程师。