短時變形測值序列的大壩安全監控模型
付 宏,李 琳,王润英(.山西省河道管护服务总站,山西 太原 03000;.河海大学水电学院,江苏 南京 0098)
短時變形測值序列的大壩安全監控模型
付 宏1,李 琳2,王润英2
(1.山西省河道管护服务总站,山西 太原 030002;2.河海大学水电学院,江苏 南京 210098)
为解决大坝短时间序列安全监测数据的建模问题,利用单独1 a的监测数据,采用基于特征正交分解的方法建立了某重力拱坝的安全监控模型,分析了模型拟合精度和预测精度,并同常规逐步回归分析方法进行了拟合和预测精度的对比分析。工程实例表明,基于特征正交分解的逐步回归分析方法可以建立短时间序列的大坝安全监控模型,其技术指标明显高于采用一般逐步回归分析所建立的模型。图7幅,表6个。
大坝安全;单年监测数据;短时间序列;安全监控模型;特征正交分解
1 概 述
统计分析是大坝安全监控模型建立的主要方法,但统计分析往往存在对样本数量和分布必须满足一定的要求,同时许多建模方法对大坝安全监控中的多重共线性问题也无能为力。针对小样本问题,目前比较多的是灰色理论建模方法和支撑向量机及其改进方法,前者对模型物理意义的分析不够明确,而后者的数学理论要求比较高 ,而且存在参数敏感性问题[1]。针对多重共线性问题,目前研究比较多的是采用偏最小二乘回归和主成分回归,上述两种方法对样本数量都有比较高的要求[2_3]。特征正交分解 (Proper Orthogonal Decomposition,POD)将线性相关的原始测值变量转化为相互独立正交的新的综合变量 (正交基)。这些正交基几乎能够涵盖原始数据的全部信息,并且正交基的个数会远小于原始变量的个数,不仅克服了原始变量的多重共线性,而且改善了矩阵病态程度,提高了模型的鲁棒性。目前基于特征分解的方法主要用于与数值方法进行配合以降低计算复杂度,尚未见到特征正交分析用于实际大坝短时间序列建模[4_11]。
2 基于特征正交分解的变形安全监控模型
2.1因子选择
大坝变形由水压分量、温度分量和时效分量构成,其回归模型为:
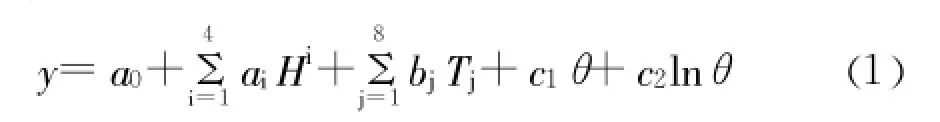
式中:a0、ai为水压因子系数;bj为温度因子系数,Tj为温度测值;θ为时效因子,θ=ti/100,ti为观测天数。
2.2基于特征正交分解的回归分析

对特征正交分解回归的参数值进行变换后求出原始数据的回归系数 Ci(i=1,2,…p),从而得到变形相对于原始自变量之间的回归方程:
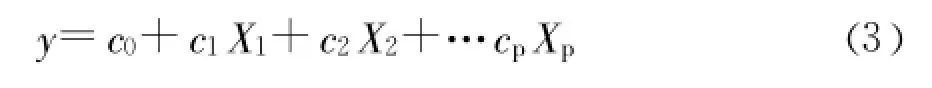
3 工程实例
3.1常规分析
某多年调节水库控制流域面积2 800 km2,总库容27.06亿m3。枢纽建筑物主要由混凝土重力拱坝、坝顶左右溢洪道、泄洪中孔、底孔、发电引水钢管、坝后式厂房等组成。最大坝高76.3 m,分28个坝块,坝顶弧长419 m,坝顶宽8 m,最大底宽53.2 m。
为检验本方法的合理性,选取本工程2013年拱冠梁和左右1/4拱,分别对应18号和左8号和26号坝段坝顶测点。
3.2基于POD的建模分析
3.2.1构造快照矩阵
为检验本文方法在短样本建模方面的效果,选择3月15日—8月1日共140组监测数据建模分析,主要分析3个测点的位移与水位、温度、时效之间的回归关系。8月2日—9月10日共40组数据验证模型的预测性。
变形包含位移、水位、温度、时效等8个自变量因子。为了消除变量量纲不同对建模的影响。首先将原始数据标准化,用Matlab软件分析自变量之间的相关性,然后用特征正交分解法通过Matlab软件提取出最佳正交基,接着用SPSS软件进行回归分析。
3.2.2计算关联矩阵
将标准化的快照矩阵通过公式 (2-11)R= (1/n)XTX用Matlab软件构造关联矩阵 (即相关系数矩阵),由计算结果可以看出各自变量之间的线性相关性比较强;如水位H与H2、H3、H4之间的相关性几乎达到1;温度 T1与 T2之间,温度与时效因子 θ、lnθ之间的线性相关性也比较强;可见上述模型如采用常规分析方法,多重共线性问题比较严重。
3.2.3求解POD最佳正交基
用Matlab软件求出关联矩阵的特征值和特征向量,将特征值以及对应的特征向量进行降序排列 ,特征值及能量随POD模态变化情况如下所示 (见图1)。
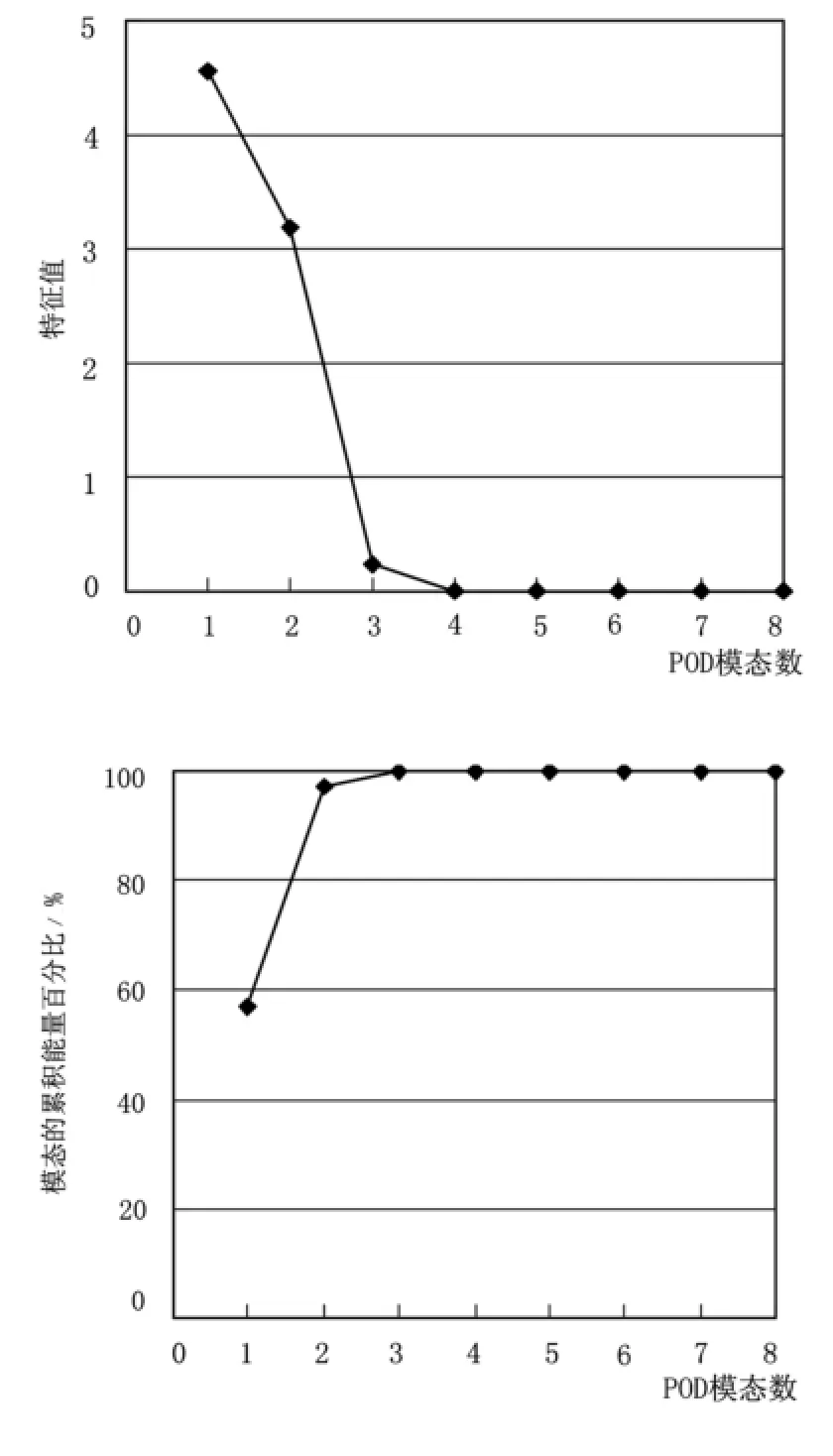
图1 特征值及能量随POD模态数目的变化情况
由图1可以看出,特征值在第三个模态的时候迅速下降,到第四个模态时几乎为零;能量到第三个模态时几乎达到100%,第一、二个模态具有较大的能量。
采用90%的能量标准对低能模态进行截断,选择POD的前两阶模态求解最佳正交基。选取特征向量构造矩阵 V=[V1,V2],将标准化的快照矩阵进行线性化叠加,提取出POD最佳正交基 Ψi(i=1,2)分别为:
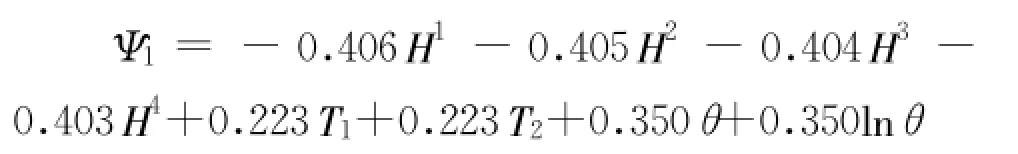

3.2.4回归分析
将拱坝3个不同测点的位移分别与得到的2个最佳正交基,利用SPSS软件进行逐步回归,分析的结果如下所示 (见表1~表3)。

表1 模型模型拟合优度

表2 建模方差分析统计
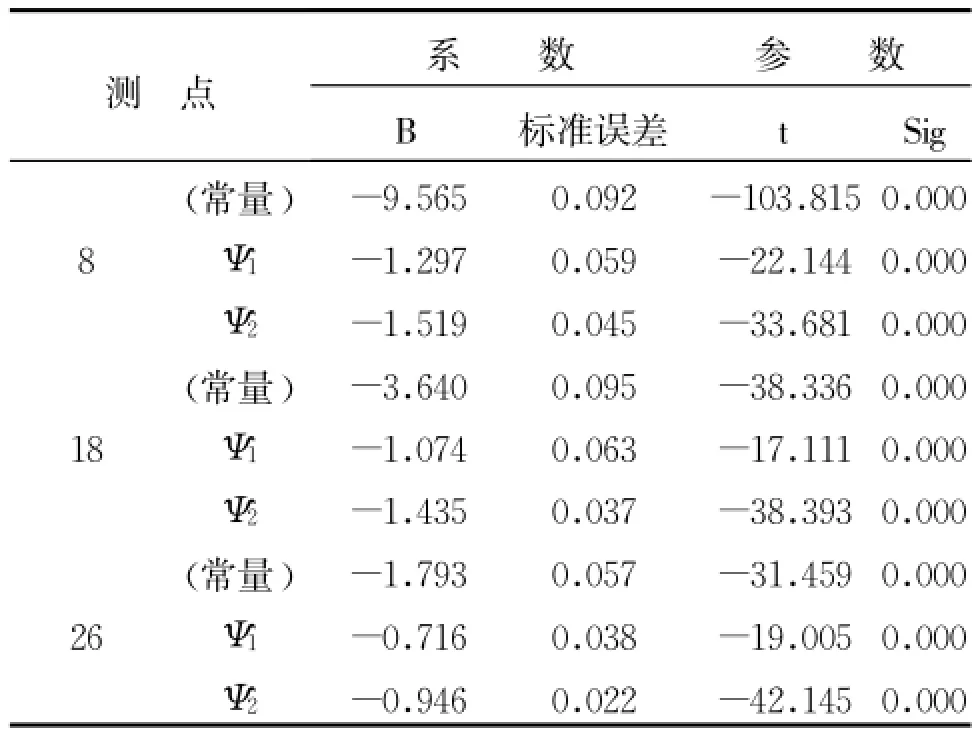
表3 回归系数估计
由表1可知,3个测点回归模型的拟合度都比较高,都在0.9以上。其中26号测点的拟合度最高,达到0.939。同时,模型的标准误差估计值都比较小,说明拟合的回归曲线与实际监测数据的分布情况比较吻合,得到的回归模型是可用的。由表2可知,各测点所得回归模型的F值均比较大,说明自变量对因变量造成的线性变动远大于随机因素对因变量的影响,自变量与因变量之间的线性相关关系比较显著。表3给出了各个测点回归模型的回归系数,3个测点的各个变量的回归系数都不相同,说明影响因子对于拱坝不同位置的位移影响程度是不同的。此外,各回归系数的显著性检验都比较小,几乎为零,都通过了检验。
通过计算得到3个测点的位移与POD正交基回归方程分别为:

将式 (4)代入式 (5)得

由最终回归方程 (6)可以看出:3个测点对应的回归系数有一定的差别,说明自变量对于每个测点位移的影响程度是不同的。同一测点,不同变量的回归系数值是不同的,温度与时效系数值要比水位的值大得多,说明温度与时效对拱坝的位移影响相对较大。为直观了解所得回归方程的合理性,给出了拟合值与实测值的对比图 (见图2~图4)。

图2 8号测点拟合值与实测值对比
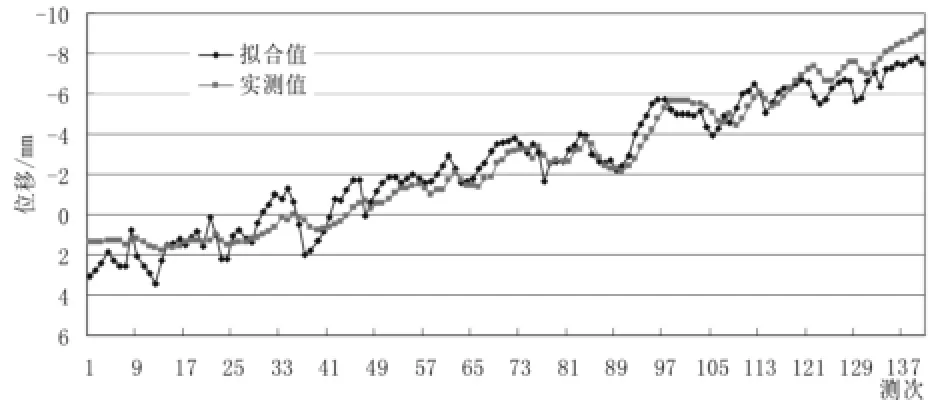
图3 18号测点拟合值与实测值对比

图4 26号测点拟合值与实测值对比
由图2~图4可以看出,整体上模型的拟合值与实测位移的拟合比较好,26号测点的拟合优度相对更好一些,进一步验证了模型的合理性。为了检验模型的预测性,选取40组标准化的监测数据代入已经得到的回归方程进行验证,其结果如下所示 (见图5~图7)。
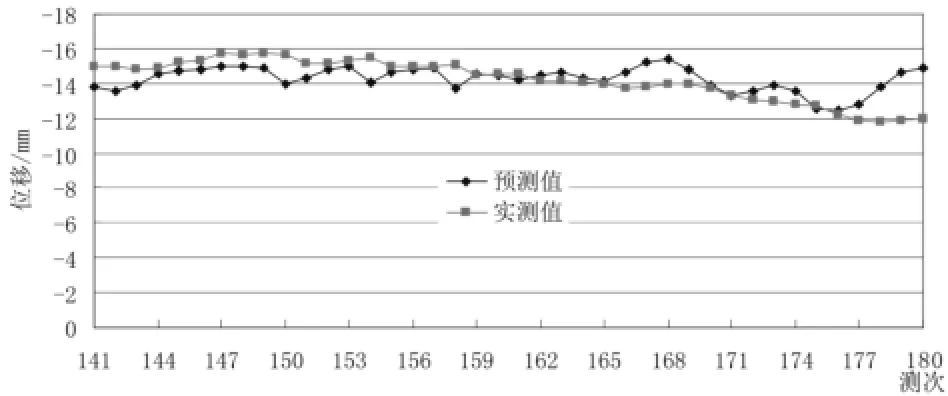
图5 8号测点预测值与实测值对比

图6 18号测点预测值与实测值对比

图7 26号测点预测值与实测值对比
由图5~图7可以看出,8号测点和26号测点的模型预测值与实测位移值相差较小,18号测点稍大一些,说明模型具有一定的预测性。3个测点模型的预测值在28测次以后与实测值相差逐渐变大,可见模型只能在一定范围内保持较好的预测性。
3.3对比分析
为了解本文模型的优越性,将上文测点实测数据采用同样因子和参数进行常规逐步回归分析,通过对模型拟合误差和预测误差2个指标对基于POD的逐步回归分析方法和常规逐步回归分析方法进行对比。各测点典型时间点的比较如下所示 (见表4~表6)。

表4 8号测点两种方法拟合和预测误差对比

表5 18号测点两种方法拟合和预测误差对比
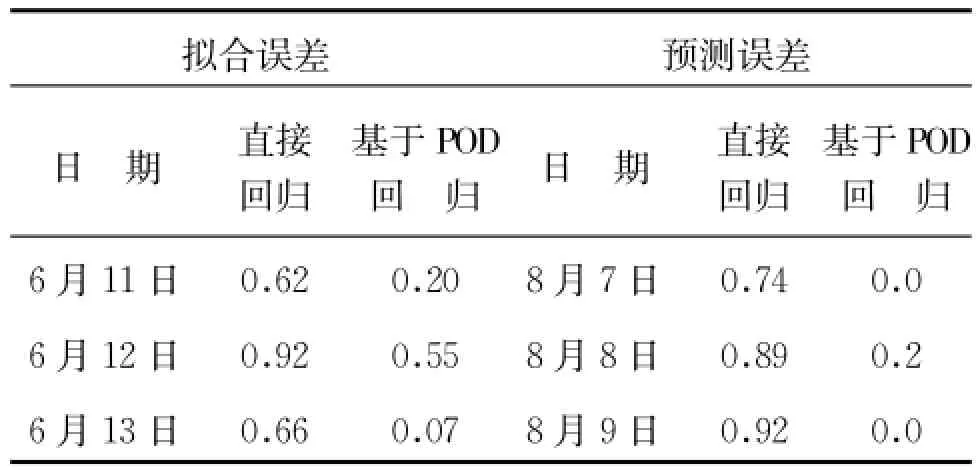
表6 26号测点两种方法拟合和预测误差对比
通过表4~表6比较可知,从与实测值的拟合误差和预测误差2个指标看来,基于POD的逐步回归分析方法明显优于常规逐步回归分析方法。
4 结 语
基于特征正交分解的方法可以有效解决小样本和因子之间的多重共线性问题,而且计算复杂度增加不大。利用某重力拱坝2013年10个月的拱冠梁和左右1/4拱的坝顶实测位移建模表明,该方法是可行的。与常规逐步回归分析方法对比说明 ,基于特征正教分解的回归模型相关指标全面优于常规的逐步回归模型。
[1] 方卫华.大坝安全监控:问题、观点与方法[M].南京:河海大学出版社,2013.
[2] 李 波.基于偏最小二乘回归的大坝安全监控统计模型的研究[D].西安:西安理工大学,2007.
[3] 刘罗曼.用主成分回归分析解决回归模型中复共线性问题[J].沈阳师范大学学报(自然科学版),2008,26 (1):42_44.
[4] 狄振华.地下水问题及基于POD方法的降维模式研究[D].北京:北京交通大学,2011.
[5] 胡 亮 .基于特征正交分解的桥梁风场随机模拟[D].武汉:华中科技大学,2007.
[6] A.Sarkar,M.P.Paidoussis.A compact limit-cycle oscillation model of a cantilever conveying fluid[J].Journal of Fluids and Structures,2003,17(4):525_539.
[7] K.Kunisch,S.Volkwein.Galerkin proper orthogonal decom-
[8] K.Kunisch,S.Volkwein.Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics[J]. SIAM Journal Numerical Annual,2002(40):492_515.
[9] B.F.Feeny,R.Kappagantu.On the physical interpretation of proper orthogonal modes in vibrations[J].Journal of Sound and Vibration,1998,211(4):607_616.
[10] Z.D.Luo,R.W.Wang and J.Zhu,Finite difference scheme based on properorthogonal decomposition for the non-stationary Navier-Stokes equations[J],Science China Ser AMath.2007(50):1186_1196.
[11] Z.D.Luo,J.Chen,I.M.Navon and X.Z.Yang,Mixed finite element formulation and error estimates based on proper orthogonal decomposition for the non-stationary Navier-Stokes equations[J].IAM Journal Numerical Analysis,2008 (47):l_19.
责任编辑 吴 昊
2016-04-22
山西省水利科学技术研究基金项目 “水库大坝安全智能监控系统关键技术研究与应用”(201402)
付 宏 (1962-),男,高级工程师,主要从事水库河道堤坝管理工作。

