层合板频率响应与声功率双目标优化设计
吴锦武,赵飞,王县委,李根
层合板频率响应与声功率双目标优化设计
吴锦武1,赵飞2,王县委1,李根1
(1. 南昌航空大学飞行器工程学院,江西南昌 330063;2. 中航航空服务保障(天津)有限公司,天津 300301)
利用遗传算法对复合材料层合板结构的固有频率间隔和辐射声功率进行双目标优化设计。利用分层理论结合有限元模型求解层合板的固有频率和振速分布。通过声辐射模态理论,计算层合板结构辐射声功率。以铺设角度作为设计变量,第一阶与第二阶固有频率间隔和辐射声功率作为双目标优化目标函数,以某4层的层合板结构为例,采用目标加权法优化目标函数。研究了不同权重系数、不同频率时固有频率间隔最大化和声功率最小化对应的优化铺设角度。由数值分析结果可知:不同的权重系数比下获得的Pareto最优解不同;在同一权重系数下,两个优化目标所起的作用不尽相同;随着频率的增加,选择相对较大的权重系数可使Pareto最优解较好地兼顾两个优化目标。
铺设角度;固有频率;声功率;遗传算法
0 引言
由于复合材料结构具有比强度大、比刚度高、材料性能可设计等特点,近年来针对复合材料层合板结构减振降噪的优化设计,越来越引起人们的关注[1-8]。随着纤维板声学特性研究的深入,纤维铺设角度是层合板结构中一个重要的结构参数,以其作为设计变量的结构优化设计也越来越多[9]。如在减振优化设计方面,Topal等[1]通过一阶剪切理论计算层合板固有频率,并以固有频率最大化为目标函数,以铺层顺序为设计变量,将改进的可行方向法(Modified feasible direction method)和有限元相结合,对层合板的铺层顺序进行了优化设计。其次,当外激励频率越高时,可将增大相邻两阶固有频率之间的间隔作为优化目标,如Adali等[2]以最大基频和最高频率间隔作为设计变量在自由振动下确定了对称层合板的最佳铺层顺序。另外Kayikci等[3]以固有频率及固有频率间隔作为目标函数,以铺设角度作为设计变量进行层合板结构优化分析。
在声优化设计方面,以层合板在外激励作用下的声辐射功率最小作为设计变量,优化复合材料铺层顺序[4-6]。其中陈炉云等[6]利用遗传算法以声辐射功率最小化为目标函数,对层合板铺设层数、厚度以及铺层顺序等进行集成优化设计。以上研究一般基于等效单层板理论分析其动力学特性。
上述研究大多数针对单一目标进行优化设计。针对实际需要,层合板结构多目标优化设计的研究越来越多[7-8]。但是大多数目标函数集中在结构强度、刚度、质量、重量等。本文拟通过分层理论结合有限元模型得到层合板结构的固有频率。基于声辐射模态得到结构辐射声功率,通过遗传算法以结构固有频率间隔与声功率同时作为优化目标函数,以铺设角度作为设计变量,对层合板结构的减振与降噪进行优化设计研究。
1 结构动力响应
基于分层理论,在沿板厚方向采用分层插值,层合板结构物理模型如图1所示。
层合板结构的位移场可表示为[10]

(2)
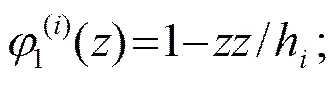
式(3)中:表示层合板的第个铺设层的厚度;为板厚的局部坐标。根据有限元理论,式(1)中,、、可表示为:
(4)
其中:
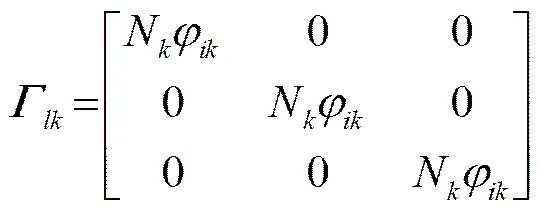
(6)
其中矩阵元素见参考文献[11]。
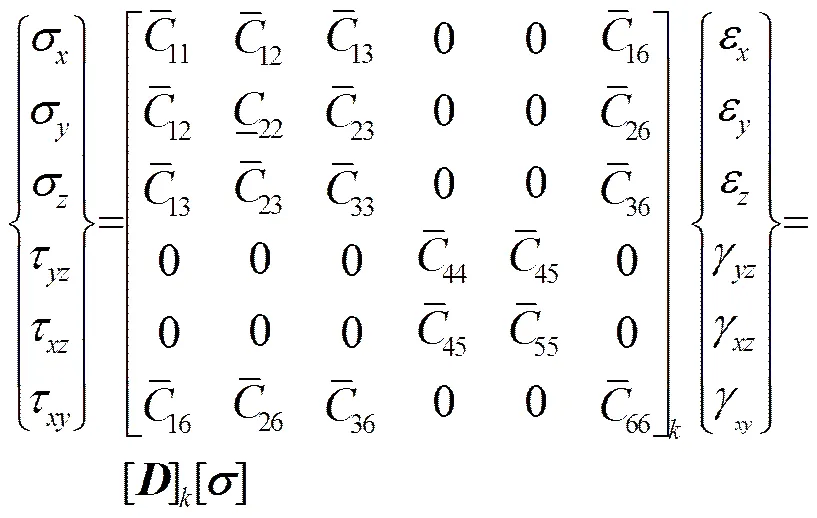
根据有限元理论,层合板结构的动力学方程为
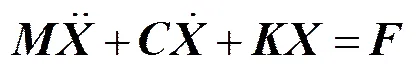
其中:为单元质量矩阵;为单元刚度矩阵;为阻尼矩阵;为单元等效节点力矩阵。由式(8)可求得结构表面法向位移、法向速度向量()。层合板的各阶固有频率可由行列式求得。
2 固有频率间隔优化
研究结构的固有频率是避免结构共振的一个重要内容。由参考文献[3]可知,为了避免结构共振,可定义固有频率间隔作为优化目标函数。频率参数[3]为:
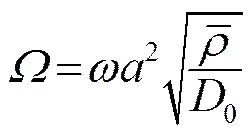
(10)
针对层合板的固有频率,取最大相邻阶固有频率间隔作为优化变量。结构-频率优化模型[11]为
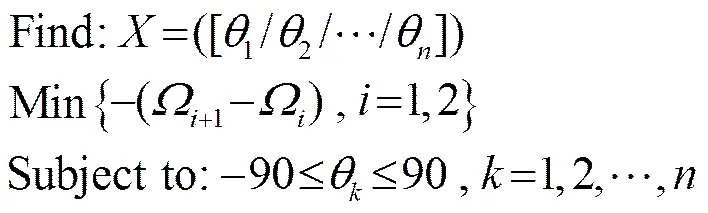
3 结构频率间隔-声辐射双目标优化模型
本文主要采用基于目标加权的遗传算法来优化目标函数:其核心思想是对目标中每一个目标向量分配一个权重,将多目标分量乘以各自的权重系数后再相加,构成一个新的目标函数,将其转化成一个单目标优化问题求解。在对每个个体取不同的权重函数的基础上,利用遗传算法求解得到多目标优化问题的多个Pareto最优解,即为多目标规划问题的有效解。
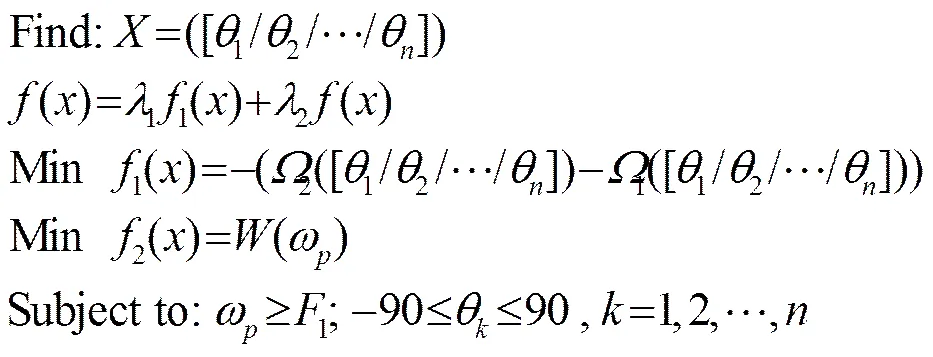
式(12)中:1表示层合板的第一阶固有频率(基频),通过取合适的1、2,使1+2=1,这样可把多目标优化问题转化成为单目标优化问题。权重系数=[1,2,…,]可反映每个目标函数的重要性。通过选取不同的权重系数,可以获得不同的Pareto最优解。
4 数值分析
以某四层碳纤维/环氧复合材料层合板为例,层合板性能参数为:长=0.3480 m,宽=0.3048 m,厚度=0.002 m,杨氏模量,,剪切模量,,阻尼比=0.05;固定激励频率=200 Hz和=500 Hz,板中心激励力大小为1,初始角度为[0º]4,利用遗传算法对复合材料层合板铺层顺序进行单目标和双目标优化设计。
4.1 固有频率间隔优化
铺设角度采用离散形式,相邻两角度之间的步长分别为90º、45º、30º、15º,初始角度为[0º]4即为[0º/0º/0º/0º],取前两阶无量纲固有频率间隔为优化变量,优化层合板铺层顺序。表1为四层层合板的优化结果。
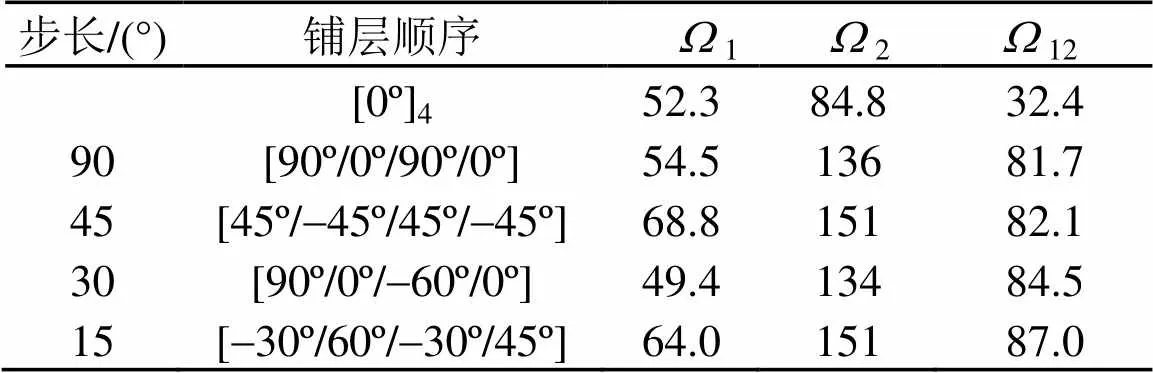
表1 不同角度步长时层合板的铺设角度优化结果
由表1可见,随着相邻两角度之间的步长减小,即角度递增量的增加,目标函数逐渐增大,从而说明角度递增量越小,优化效果越好;但随着角度递增量的减小,计算量成倍的增加,寻找全局最优解将变得越来越困难,因此在实际应用过程中目标函数的角度递增量要根据实际情况灵活选取。
4.2 声功率最小化优化
仍以上述结构为例,以结构辐射声功率最小作为目标,采用遗传算法优化层合板铺层顺序,初始角度分别为[0º]4、[0º]8。表2为激励频率和时层合板铺层顺序优化结果。
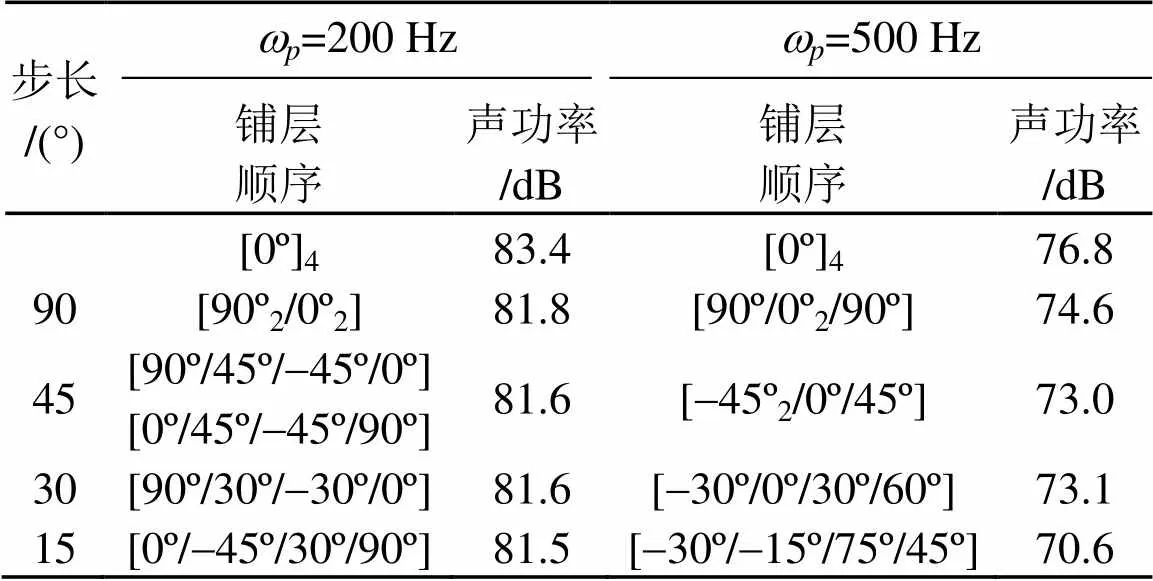
表2 激励频率wp=200 Hz和wp=500 Hz层合板铺层顺序优化
由表2可见,通过对层合板铺层顺序的优化,其声辐射功率级在激励频率为200 Hz时降低了1.9 dB,激励频率为500 Hz时降低了6.2 dB。说明通过铺设角度优化可使层合板结构具有良好的降噪效果。这与复合材料的各向异性有关。
4.3 双目标优化
对于固有频率间隔与声功率双目标优化,主要的是选择合适的权重系数1、2。本文选取如表3和表4中的12个权重系数比计算上述层合板的铺层顺序双目标优化的Pareto最优解,由于实际层合板结构45º铺设角度偏多,同时为了减少计算工作量,故层合板的铺层角度选择区间为[-45º,0º,45º,90º]四个离散值。
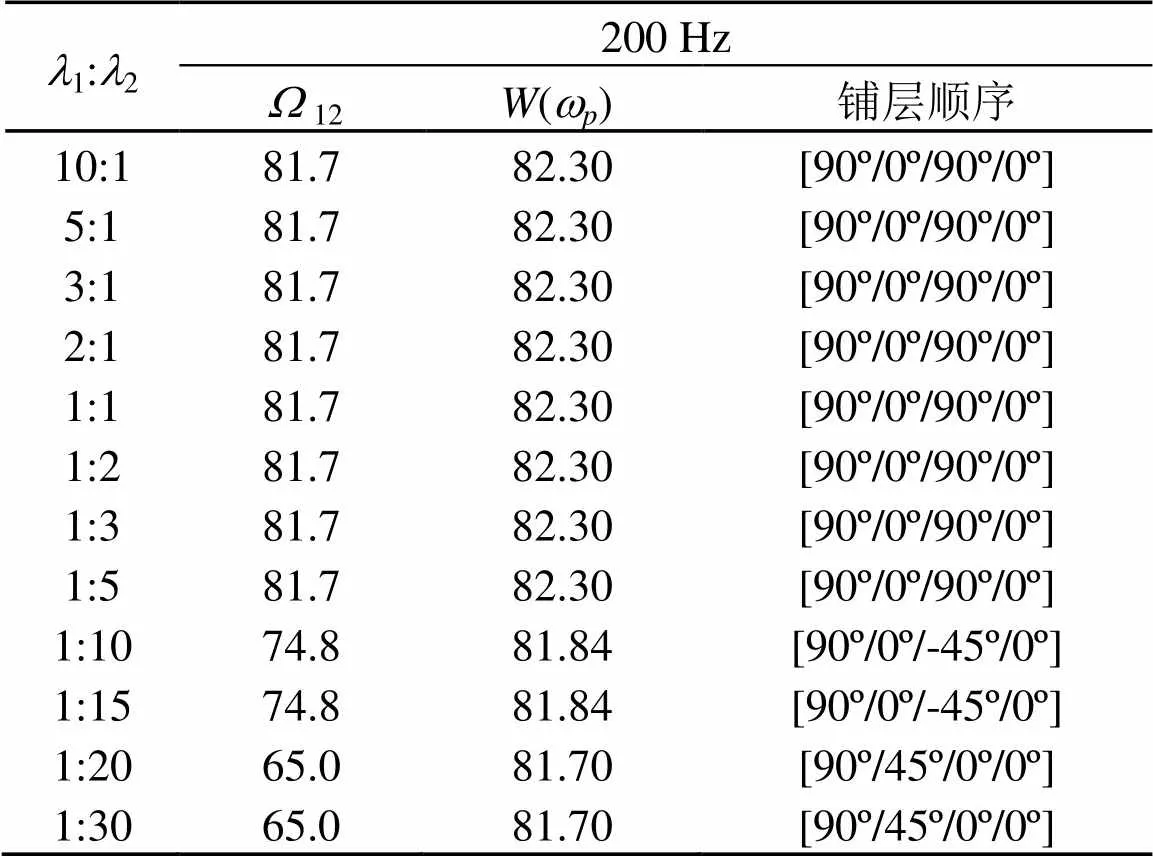
表3 不同权重系数比的双目标优化Pareto最优解(200 Hz)
由表3、4可见:不同的权重系数比下获得的Pareto最优解不同,因此本文分别选取权重系数比1:2分别为1:1、1:10,1:20做详细讨论。
从表3和表4可知:在相同频率下,权重系数从小于1:10开始,随着权重系数的变小,优化后的目标函数和()数值随之大幅度变小。当权重系数在10:1到1:5之间,优化后的目标函数和()结果相同,相应的优化设计变量(即铺设角度)也一致。当权重系数大于1:10时,优化后的目标函数数值相差较大。
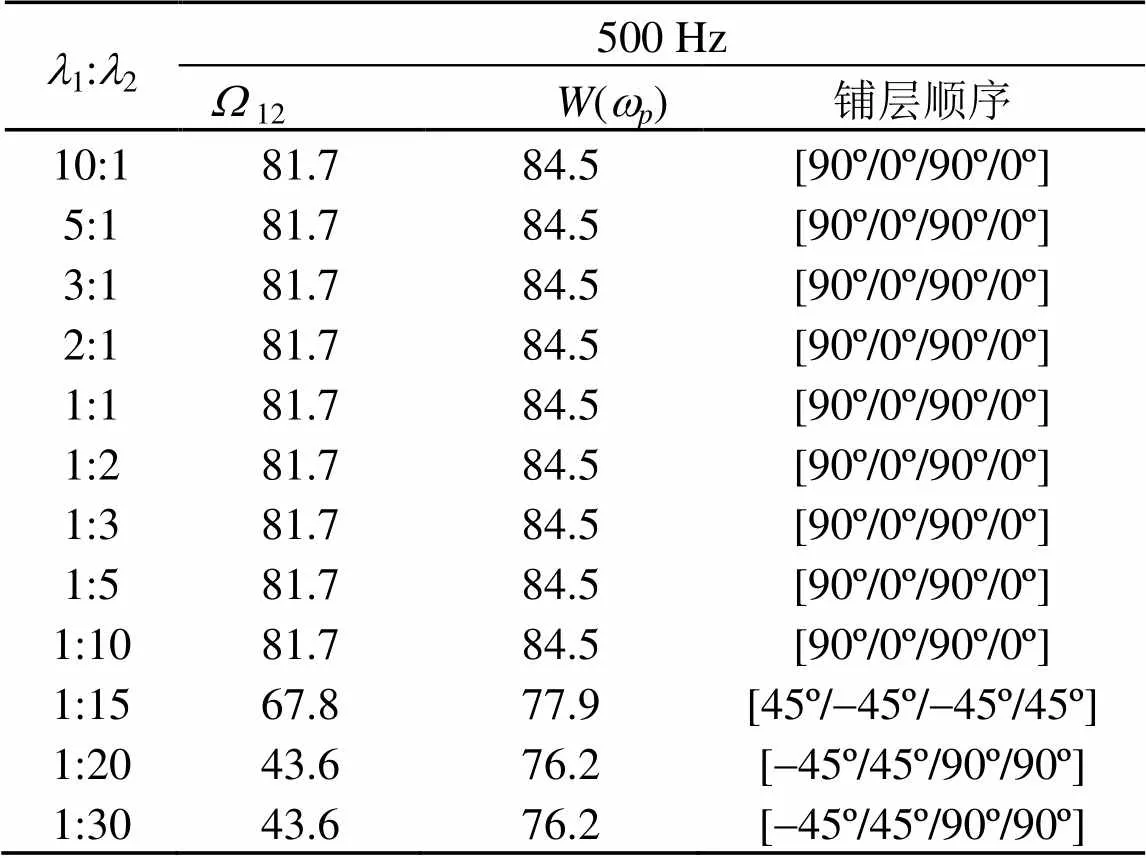
表4 不同权重系数比的双目标优化Pareto最优解(500 Hz)
表5~7分别表示权重系数取1:2=1:1、1:10,1: 20时,激励频率=200 Hz时层合板铺层顺序多目标优化结果。
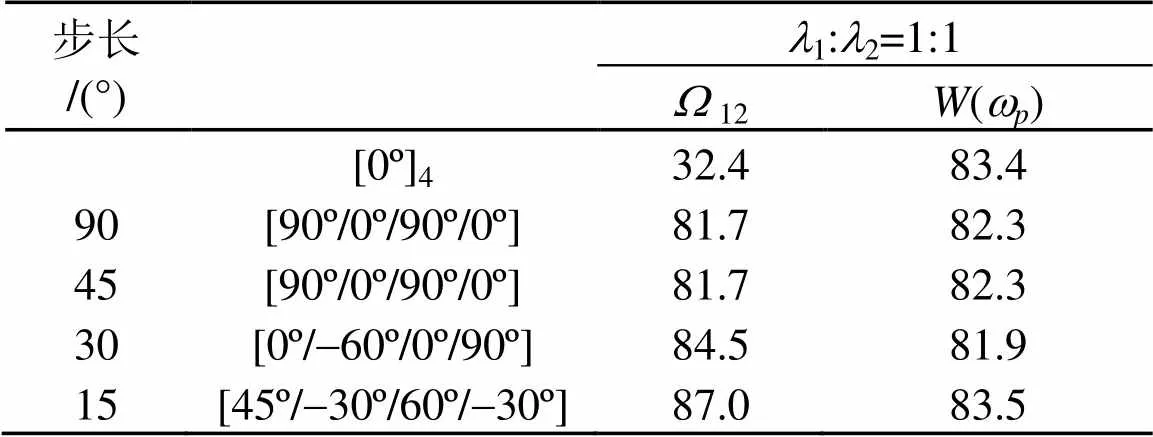
表5 激励频率wp=200 Hz多目标铺设角度优化(l1:l2=1:1)
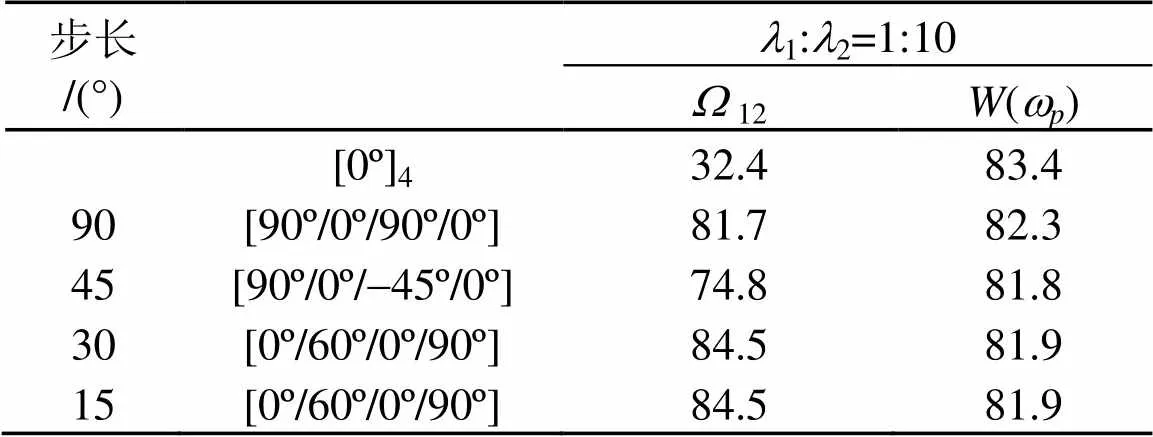
表6 激励频率wp=200 Hz多目标铺设角度优化(l1:l2=1:10)
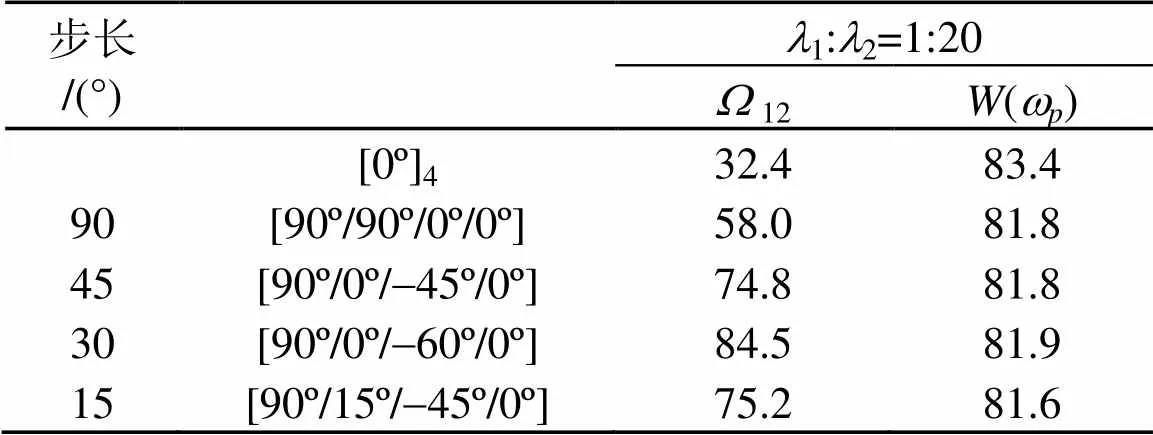
表7 激励频率wp=200 Hz多目标铺设角度优化(l1:l2=1:20)
从表5~7可知:随着1:2的增大,相同角度步长时的声功率数值也逐渐减小。
由表5~10可知,当权重系数比1:2=1:1时,两个优化目标中所起的作用明显远远大于声辐射功率,以至于最终优化结果与频率间隔单目标优化时的结果基本一致,导致声辐射功率过大,激励频率为500 Hz时尤其明显。当权重系数比增大到1:2=1:10甚至是1:20时,两个优化目标对最终结果的贡献趋近于相等。因此在200 Hz外激励下,选择权重系数比1:2=1:20,而在500 Hz外激励下,权重系数比1:2选择1:10比较合适。
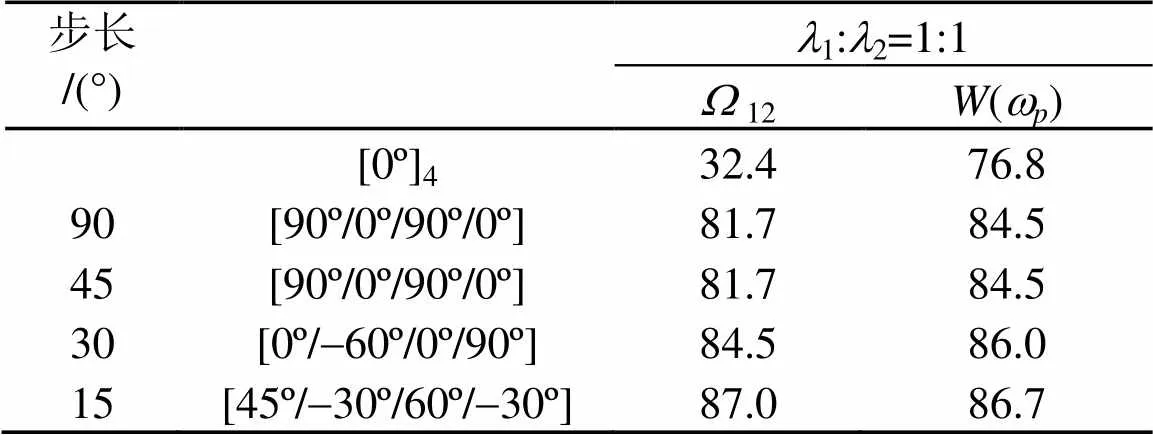
表8 激励频率wp=500 Hz多目标铺设角度优化(l1:l2=1:1)
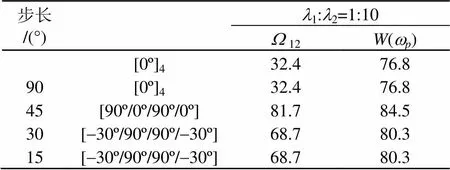
表9 激励频率wp=500 Hz多目标铺设角度优化(l1:l2=1:10)
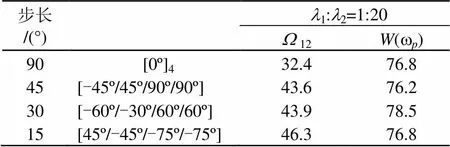
表10 激励频率wp=500 Hz多目标铺设角度优化(l1:l2=1:20)
层合板在200 Hz外激励下,权重系数比1:2=1:20时的遗传算法迭代过程如图2所示。在500 Hz外激励下,权重系数比1:2选择1:10时的遗传算法迭代过程如图3所示。从图2、3可知:
在角度步长一致的情况下,外激励频率越高,同一参数优化计算需要的迭代次数越多。另外,角度步长越小,种群均值收敛速度越慢,其中角度步长为90°时,种群均值收敛速度最快。
(a) 90°
(b) 45°
(c) 30°
(d) 15°
图2. 不同递增角度的层合板多目标优化迭代过程(=200 Hz、1:2=1:20)
Fig.2 Iteration process of double objective optimization(=200 Hz、1:2=1:20)
(a) 90°
(b) 45°
(c) 30°
(d) 15°
图3 不同角度步长的层合板多目标遗传算法迭代过程(=500 Hz、1:2=1:10)
Fig.3 Iteration process of double objective optimization(=500 Hz、1:2=1:10)
在200 Hz外激励下,权重系数比1:2=1:20时的Pareto最优解较好地兼顾了两个优化目标,即对应优化角度分别为:[90º/90º/0º/0º]、[90º/0º/-45º/0º]、[90º/0º/-60º/0º]以及[90º/15º/-45º/0º]。在以上四种优化角度下,层合板结构在全频段内的声功率如图4所示。为了对比,图4中增加了[0º]4铺设角度下对应的声功率。
由图4可知:四种铺设角度的对应的声功率最大值基本相同。另外对照表5所示内容,由图4也可知,[90º/15º/-45º/0º]铺设角度下的基频最小为82 Hz,同时频率间隔最大。而[90º/90º/0º/0º]铺设角度下的基频最大为100.6 Hz,同时频率间隔最小。
在500 Hz外激励下,权重系数比1:2=1:10时对应的优化角度分别为[0º]4、[90º/0º/90º/0º]以及[-30º/90º/90º/-30º]。根据上述三种优化铺设角度,计算可得到层合板结构前10阶固有频率,如表11所示。
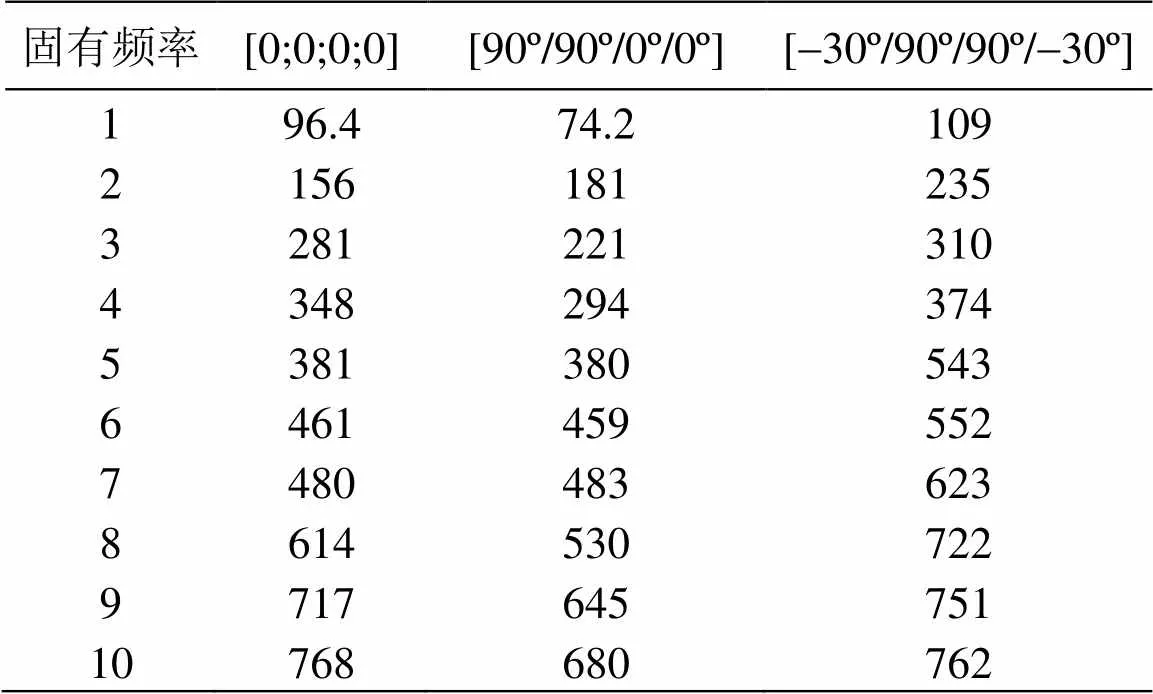
表11 激励频率wp=500 Hz层合板前10阶固有频率(l1:l2=1:10)
另外,500 Hz三种优化角度下结构在全频段内的声功率如图5所示。
由图5可知:三种铺设角度的对应的声功率最大值基本相同。[0º]4铺设角度下的基频最小为82 Hz,而且频率间隔最小。[90º/90º/0º/0º]铺设角度下的基频最大,为100.6 Hz,频率间隔也最大。同时当频率超过700 Hz时,随着频率的增高,三种铺设角度下的层合板声功率基本一致。
综上所示,选择适当铺设角度以及权重比,可使层合板结构在减振和降噪方面同时得到优化。
5 结论
(1) 通过分层有限元模型可计算得到层合板结构的固有频率。
(2) 通过遗传算法,选择合适的铺设角度可进行复合材料层合板结构声功率的最小化设计。
(3) 选择合适的权重系数,可实现层合板结构的减振和降噪双目标优先,改善层合板的声振特性,为实际复合材料的设计与应用提供参考。
[1] TOPAL U, UZMAN ü. Frequency optimization of laminated skew plates [J]. Materials and Design, 2009, 30(8): 3180-3185.
[2] ADALI S, VERIJENKO V E. Optimum stacking sequence design of symmetric hybrid laminates undergoing free vibrations[J]. Composite Structures, 2001, 54(3): 131-138.
[3] KAYIKCI R, SONMEZ F O. Design of composite laminates for optimum frequency response[J]. Journal of Sound and Vibration, 2012, 331(8): 1759-1776.
[4] DU Jianbin, OLHOFF. N. Minimization of sound radiation from vibrating bi-material structures using topology optimization. Structural and Multidisciplinary Optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(5): 305-321.
[5] Duhring M B, Jensen J S, Sigmund O. Acoustic design by topology optimization[J]. Journal of Sound and Vibration, 2008, 317(5): 557-575.
[6] 陈炉云, 张裕芳. 基于遗传算法的复合材料结构-声辐射优化研究[J]. 复合材料学报, 2012, 29(3): 203-207.
CHEN Luyun, ZHANG Yufang. Composite material structural-acoustic optimization on genetic algorithm[J]. Acta Material Compositae Sinica. 2012, 29(3): 203-207.
[7] PELLETIER J L, VEL. S S, Multi-objective optimization of fiber reinforced Composite laminates for strength, stiffness and minimal mass [J]. Computers & Structures, 2006, 84(29-30): 2065-2080.
[8] RAHUL Sandeep G, CHAKRABORTY D. Multi-objective optimization of hybrid laminates subjected to transverse impact[J]. Composite Structures, 2006, 73(3): 360-369.
[9] 王佐民, 俞悟周. 铝纤维板共振结构声学特性的理论分析[J]. 声学技术, 2005, 24(3): 183-185.
WANG Zuomin, YU Wuzhou. Theoretical annlysis on acoustical characteristics aluminum fiberboard[J]. Technical Acoustics, 2005, 24(3): 183-185.
[10] REDDY J N. Mechanics of laminated composite plates and shells [M]. New York: CRS Press, 2004: 96-97.
[11] 赵飞. 基于分层理论的层合板声辐射分析与结构优化[D]. 江西: 南昌航空大学, 2013: 11-39.
ZHAO Fei. Sound radiation analysis and structure optimization of laminated plates based on layerwise theory [D]. Jiangxi: Nanchang Hangkong University, 2013:11-39
Double objective optimization of frequency response and acoustic power for laminated composite plates
WU Jin-wu1, ZHAO Fei2, WANG Xian-wei1, LI Gen1
(1.School of Aircraft Engineering, Nanchang Hang Kong University, Nanchang330063,Jiangxi,China;2. Aviation Service Assurance Ltd, Aviation Industry Corporation of China, Tianjin300301, China)
Both the separation between two adjacent natural frequencies and the sound power of laminated composite plate are optimized by use of genetic algorithm in this paper. The layer-wise finite element model is imposed to determine the natural frequencies and the velocity distributions of laminated composite plates. Based on the acoustic radiation model, sound power is calculated. The fiber laying angles are chosen as design variables and the design objective is to minimize the sound power and to maximize the separation of two adjacent natural frequencies. A four-layer laminated plate are used as examples, the objective weighting method is used to optimize the objective function. And the optimal laying angles with sound power minimization and frequency separation maximization are discussed under different frequencies and different weight coefficients. The numerical simulations show that there are different Pareto optimal solutions under different weight coefficients. With frequency increasing, a relatively large weighting coefficient can be chosen for the Pareto optimal solution to balance the two optimization objectives.
the laying angle; natural frequency; sound power; genetic algorithm
TB332 TH113.1
A
1000-3630(2016)-02-0155-07
10.16300/j.cnki.1000-3630.2016.02.0013
2015-04-03;
2015-07-14
国家自然科学基金资助项目(51265038)
吴锦武(1976-), 男, 江西高安人, 博士, 教授, 研究方向为机械振动与声控制。
吴锦武, E-mail: jinwu.w@hotmail.com

