波束锐化技术在多波束测深声呐中的应用
魏波,沈嘉俊,周天,李海森
波束锐化技术在多波束测深声呐中的应用
魏波1,2,沈嘉俊1,2,周天1,2,李海森1,2
(1. 哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨 150001;2. 哈尔滨工程大学水声工程学院,黑龙江哈尔滨 150001)
针对常规波束形成器的分辨性能和旁瓣性能间的矛盾,研究了超波束形成器的波束特征以及空间分辨性能。通过计算机仿真验证了加权超波束形成器既有较高的空间分辨力,又有良好的旁瓣特性。通过对外场实验数据的处理,验证了该算法对于多波束测深声呐测量结果中存在的“隧道效应”假象具有明显的抑制作用。针对算法实现结构进行了优化,进一步减小了算法复杂度。利用DSP进行了算法实现,算法具有较好的实时性和工程实用性。
波束锐化;超波束;分辨力;隧道效应
0 引言
常规波束形成器(Conventional BeamForming, CBF)能够对指定到达方向的回波信号进行增强,对噪声进行抑制,原理简单、算法易实现,因而在多波束声呐中得到了广泛的应用。但该波束形成器具有主瓣波束宽、旁瓣级高、存在能量泄漏的缺点,容易引起旁瓣干扰。多波束测深声呐的探测目标是大面积海底,垂直入射的海底回波波束能量很强,能量泄露进入其他波束的主瓣方向后,很容易形成旁瓣干扰。当被测量的海底比较平坦且底质较硬时或空间方位较近时,这种影响更加明显。当使用基于波束输出能量的时间加权平均(Weighed Mean Time, WMT)等海底检测算法时,其影响就是会把平坦海底地形测量成虚假的两边上翘的弧形海底地形,即所谓的“隧道效应”(Tunnel effect)[1-3],如图1所示。
抑制“隧道效应”对提高多波束测深声呐的数据质量和测量结果的可信度非常重要,目前常见的解决方法有两类:第一类采用自适应旁瓣抵消器,如文献[4-5]提出利用误差反馈格型递归最小二乘(Recursive Least Squares,RLS)算法和基于Givens旋转的后验格型-梯型算法对多波束测深声呐实验数据中存在的旁瓣干扰进行分析处理;文献[6]针对文献[4,5]所提算法存在抵消部分真实信号的缺陷,提出RLS-Laguerre算法并进行实测数据处理,文献[7]将此算法由波束包络抵消扩展到波束复输出抵消,提出利用广义旁瓣抵消(Generalized Side-lobe Canceller,GSC)结构对“隧道效应”进行消除,并利用与其等效的最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)算法对试验数据进行处理。上述算法能够有效地削弱边缘波束方向上镜像波束的旁瓣干扰,但算法的结构复杂,运算量较大,难以实时实现;第二类采用对CBF进行加窗的算法,如切比雪夫窗、卷积矩形窗等[1-2],虽然有效降低了旁瓣,但导致主瓣展宽,降低了空间分辨力。增大声呐基阵孔径可以有效缓解这一矛盾,但其导致硬件复杂、高成本和声呐小型化趋势相矛盾。因此,利用信号处理方法降低波束旁瓣,并且还能保证波束主瓣的尖锐,不失为一种很有吸引力的、值得研究的途径。文献[8]比较了相关信号处理方法,其中涉及了一种超波束形成技术(Hyper BeamForming, HBF)[9],利用子阵波束的组合能够实现波束主瓣的锐化,且运算量和常规波束形成器相当,具有较强的实用性。
文献[10]对超波束形成技术进行了仿真研究,文献[11]结合后置处理算法对其实现形式进行了修正,文献[12]将超波束形成技术应用于圆阵。本文进一步仿真研究超波束形成器的空间分辨能力,并基于其主窄瓣且旁瓣低的特点,将该技术应用于多波束测深声呐“隧道效应”抑制。在研究超波束形成算法的基础上,对算法结构进行优化,进一步减小算法复杂度,并在DSP硬件平台上对算法实时性进行了测试。
1 超波束形成技术
1.1 HBF技术原理
基阵结构如图2所示,令坐标(+1/2,0)处的接收回波表示为,入射方向为,则第i阵元接收信号为:

(2)
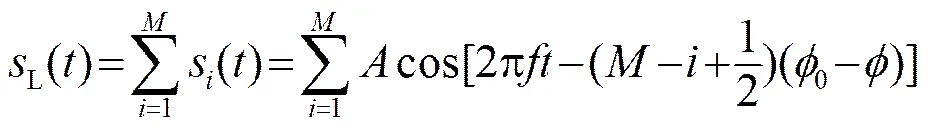
(4)
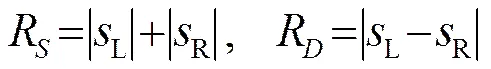
超波束形成公式为
(6)
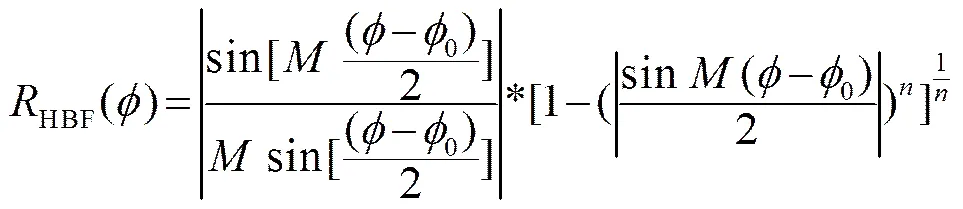
波束形成器在大角度时波束宽度将变宽,为实现空间上的均匀扫描,保证方向分辨力的一致性,需要对外侧波束进行锐化处理以实现恒定束宽,这可以通过对式(6)中超系数取不同值来实现。
1.2 HBF空间分辨性能仿真
在研究超波束形成算法的基础上,利用计算机仿真对比CBF、加窗CBF以及HBF的空间分辨性能。仿真中以能够区分空间两个等强度、相临目标的最小夹角为评价标准,取波束图案上两目标间幅值下降3 dB作为分辨准则。
相关仿真条件:信号形式为CW脉冲;CBF为相移波束形成器;换能器基阵形式为64元直线阵;阵元间距取半波长。
1.2.1 CBF分辨力分析
对回波信号直接进行相移波束形成,分别选取在0°和50°附近的回波目标,观察在大角度区域及小角度区域的波束形成输出,见图3、4。
由图3可见,位于小角度区域的两空间目标方位可分极限为-0.67°和0.67°;由图4可见,位于较大角度区域的两空间目标方位可分极限为-50°和-52.13°。显然,常规波束形成器随扫描角度增大,波束展宽,分辨力下降,并且旁瓣较高(第一旁瓣仅为-10 dB),很可能导致明显的“隧道效应”。
1.2.2 加窗CBF分辨力分析
为了降低旁瓣,对CBF加切比雪夫窗,主旁瓣比达-40 dB,观察不同回波角度情况下的波束输出结果,仿真结果如图5、图6所示。
由图5可见,两空间目标方位可分极限为-0.735° 和0.735°;由图6可见,两空间目标方位可分极限-50°和-56.095°。虽然与CBF相比旁瓣较低,有利于抑制“隧道效应”,但是加窗处理会导致波束展宽,尤其是随着目标方位角度的加大,分辨力下降十分严重。然而在现有的设备条件下,为了保证测深数据准确和抑制“隧道效应”,加窗处理依然有必要。
1.2.3 HBF分辨力分析
按照上述超波束理论进行仿真,不同回波到达角度条件下的波束输出如图7、8所示。
由图7可见,两空间目标方位可分极限为-0.626°和0.626°;由图8可见,两空间目标方位可分极限为-50°和-51.978°。相对于加窗CBF,超波束形成的空间分辨力有了明显改善。
2 超波束在多波束测深中的应用
2.1 恒定束宽超波束形成
从图7、8可以看到,距离目标方位越近的波束旁瓣越低,而“隧道效应”的特性正是旁瓣对距离目标方位越近的波束影响越明显。图9给出了单目标时的波束图。可见,HBF的旁瓣变化特征能够有针对性地抵消“隧道效应”产生的影响。
多波束测深声呐具有一定的覆盖宽度,外侧波束束宽会发生变化。为了保证式(7)的输出波束具有恒定的束宽,需要在不同的预成波束方向采用不同的超系数,以保证外侧波束的尖锐性。由式(7)推导出恒定束宽条件下的公式(8):
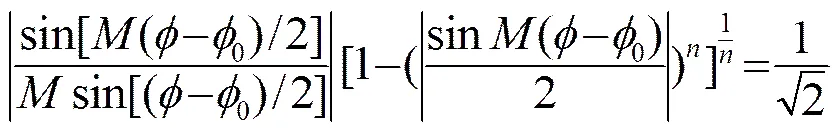
将预成波束角度分别代入公式(8)中,利用逐次迭代法可以计算出误差值最小的方程数值解,不同波束方向的超系数如图10所示。
方位角/(°)
图10 超系数变化曲线
Fig.10 Curve of hyper coefficient
2.2 超波束算法优化及其DSP实现
超波束形成算法中存在未知底数与未知幂的指数运算,计算复杂度较高,占用了大量的处理时间,为了进一步提高算法的实时性,需要对式(6)的算法实现结构进行优化,两边取以10为底的对数:
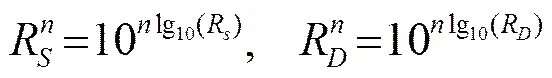
(10)
按照公式(9)、(10)可以将未知底与未知幂的指数运算简化成一次以10为底数的幂级数运算与一次以10为底数的对数运算组合,算法结构有利于DSP的高速运算,对数简化方法结构如图11所示。
为了满足实际工程需求,并且验证算法的实时性,本文在哈尔滨工程大学研制的国产多波束测深声呐设备信号处理平台上进行了超波束形成的DSP实现。信号处理器选取TI公司推出的定/浮点处理器TMS320C6748,工作主频为420 MHz,进行256波束的超波束形成。
按照传统的DSP计算方法,直接用公式(6)进行波束循环计算需要耗费较多的时间。针对选取的TMS320C6748,可利用TI公司提供的自适应定/浮点运算的DSPLIB运算库,能够进行向量化的数据计算,节省出大量的数据寻址时间。分别在软件仿真与硬件平台上实现256波束的超波束形成,算法整体运行时间对比如表1所示。

表1 按照不同方法运算的运行时间比较(单位: us)
由表1可以看出,利用对数简化的处理方法,能够有效地提升算法处理效率,尤其是在硬件实现过程中,需要进行大量的数据寻址、存储过程,对数简化向量处理方法能够有效提升算法的实时性。
对于公式(9)、(10)的推导过程,可以使用以任意常数为底的对数形式,DSPLIB常用的对数、指数函数为自然对数底、以10为底和以2为底。公式中以何数为底并不影响结果,所以分别验证不同底数下的运算时间,进一步提升算法的实时性。分别在软件仿真与硬件平台上实现256波束的超波束形成,算法整体运行时间对比如表2所示:

表2 按照不同对数底运算的运行时间比较(单位:us)
由表2可以看出,不同底数情况下算法运算时间是不同的。由表1、2可知,在不影响计算精度的前提下,选取适当的运算方式有助于在采样间隔内实时完成回波信号的超波束形成运算。经简化后的超波束形成算法可以在采样率的采样间隔内实时完成,实时处理效果如图12所示。
3 多波束测深实验数据处理
为了验证超波束形成在多波束测深声呐中的应用效果以及对“隧道效应”的抑制效果,利用哈尔滨工程大学研制的国产多波束测深声呐设备进行外场实验,并对实验数据进行处理。
多波束测深声呐基元数为64,信号频率为300 kHz,阵元间距为半波长,发射信号脉宽为0.1 ms,4倍水深覆盖。采用上述三种波束形成器对某水域外场实验数据进行波束形成处理,并使用WMT算法进行水底深度检测。
3.1 常规波束形成数据处理
利用常规相移波束形成进行数据处理,波束输出序列及深度检测结果如图13、14所示。
从图13可以看出常规波束形成存在很严重的旁瓣干扰,有多个较强回波方向的旁瓣泄漏到较弱回波的主瓣方向。从图14中可以看到,由于“隧道效应”导致检测出现多角度的虚假目标,深度检测结果存在较大误差。
3.2 加窗波束形成数据处理
利用切比雪夫窗对常规相移波束形成进行加窗处理,波束输出序列及深度检测结果分别如图15、16所示。
比较图14、16可以发现,CBF加窗对“隧道效应”具有一定的抑制作用,虚假目标减少,但其影响依然存在,检测结果误差较大。
3.3 超波束形成数据处理
利用超波束形成进行数据处理,超系数按照预成角度选择不同参数,波束输出序列及深度检测结果分别如图17、18所示。
从图17、18中可以明显看出,在HBF的输出中已经难以看出旁瓣干扰,“隧道效应”得到了有效地抑制。
3.4 数据处理效果对比
为了更清楚地说明这一问题,从上述三种处理方法中,抽取某一时间片下各波束角度输出,显示于图19、20中。
从图19、20中可以看出,CBF、加窗CBF都有较强的旁瓣干扰,在其他波束方向上产生虚假目标。HBF能够有效地抑制“隧道效应”,在各波束上反映出真实的回波到达方向。
类似的,从上述三种处理方法中,抽取波束角度35.33º的波束输出时间序列,显示于图21、22。
从图21、22中可以看出,CBF、加窗CBF都有明显的旁瓣干扰,在时间序列上产生较强的虚假回波,这将导致时间加权平均算法检测误差,出现弧形的“隧道效应”虚假目标。HBF能够有效地抑制“隧道效应”,在时间序列上反映出真实的回波能量状态,确保时间加权平均算法的准确性。
4 结论
波束锐化技术应用于多波束测深声呐既保证了较高的空间分辨力,又大大降低了旁瓣,很好地抑制了“隧道效应”。由于超波束形成技术的计算量和CBF相当,经算法简化后运算复杂度进一步减小,算法结构很容易在DSP上实现。配合定/浮点系列DSP处理器,算法的实时性和工程实用性得到了保证,易于应用到国产多波束测深声呐系统中,有望进一步提升测深结果的有效性。
[1] CHEN Baowei, LI Haisen, WEI Yukuo, et al. Tunnel effect elimination in multi-beam bathymetry sonar based on apFFTalgorithm[C]//Proceedings of ICSP’10. Beijing, China, 2010: 2391- 2394.
[2] 陈宝伟. 超宽覆盖多波束测深技术研究与实现[D]. 哈尔滨: 哈尔滨工程大学, 2012.
CHEN B W. Research and implementation of the tech-nology for super-wide coverage multibeam bathymetry[D]. Harbin: Harbin Engineering University, 2012.
[3] 李海森, 周天, 徐超. 多波束测深声呐技术研究新进展[J]. 声学技术, 2013, 32(2): 73-82.
LI Haisen, ZHOU Tian, XU Chao. New developments on the technology of multi-beam bathymetric sonar[J]. Technical Acoustics, 2013, 32(2): 73-82.
[4] WENG Ningning, LI Haisen, YAO Bin, et al. Tunneleffect in multi-beam bathymetry sonar and its canceling witherror feedback lattice recursive least square algorithm[C]//Oceans’08 MTS/IEEE Conf. Kobe, Japan, 2008.
[5] LI Haisen, YAO Bin, WENG Ningning, et al. Performanceanalysis and application of posteriori lattice-ladder algorithmbased on Givens rotation[C]//Proceedings of ICSP’08. Beijing, China, 2008.
[6] 魏玉阔, 翁宁宁, 李海森, 等.利用RLS_Laguerre格型算法消除多波束测深声呐的隧道效应[J].哈尔滨工程大学学报, 2010,31(5): 547-552.
WEI Yukuo, WENG Ningning, LI Haisen, et al. Eliminating the tunnel effect in multi-beam bathymetry sonarby using the recursive least square-Laguerre lattice algorithm[J] Journal of Harbin Engineering University, 2010, 31(5): 547-552.
[7] 魏玉阔, 陈宝伟, 李海森. 利用MVDR算法削弱多波束测深声呐的隧道效应[J]. 海洋测绘, 2011, 31(1): 28-31.
WEI Yukuo, CHEN Baowei, LI Haisen. Tunnel effect elimination in multibeam bathymetry sonar based on MVDR algorithm[J]. Hydrographic Surveying And Charting, 2011, 31(1): 28-31.
[8] Gopi Ram, Durbadal Mandal, RajibKar, et al. Optimized hyper beamforming of linear antenna arrays using collective animal behaviour[J]. The Scientiic World Journal, 2013(5): 1903-1912.
[9] Heiko Schlieter. Passive sonar detection improvement by hyperbeamtm technique[C]//UDT, Europe 2006, Hamburg, Germany, 2006: 7A-2.
[10] 聂良春. 超波束(HBF)用于波束锐化[J]. 声学技术, 2008, 27(6):892-895.
NIE Liangchun. Hyper beamforming (HBF) technique for beam narrowing[J]. Technial Acoustics, 2008, 27(6): 892-895.
[11] 王昭辉, 刘云涛, 蔡惠智. 基于修正超波束技术的精确定向算法探讨[J], 声学技术, 2009, 28(5): 651-654.
WANG Zhaohui, LIU Yuntao, CAI Huizhi. Research on the algorithms of accurate bearing estimation based on modified hyper-beam technique[J]. Technial Acoustics, 2009, 28(5): 651-654.
[12] 徐伟东, 章新华, 李澍. 超波束技术的一种新的改进方式[J]. 声学技术, 2014, 33(5): 168-172.
XU Weidong, ZHANG Xinhua, LI Shu. A new improvement method of hyper beamforming technology[J]. Technial Acoustics, 2014, 33(5): 168-172.
Application of beam narrowing technique in multi-beam bathymetric sonar
WEI Bo1,2, SHEN Jia-jun1,2, ZHOU Tian1,2, LI Hai-sen1,2
(1. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001,Heilongjiang,China;2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001,Heilongjiang,China)
For conflict existing between resolution and sidelobe influence in the conventional beamformer(CBF), the article mainly studies beam features and spatial resolution of hyper-beamformer(HBF). Computer simulation results demonstrate that HBF can synchronously improve spatial resolution and reduce sidelobe. Processing results of the sea trial data verify that the algorithm can restrain the tunnel effect illusion in multi-beam bathymetric results effectively, and the algorithm has low computational load, good real-time performance and practicability. The algorithm has been evaluated on the platform of DSP and proved to be useful and real-time.
beam narrowing; hyperbeam; resolution; tunnel effect
P715.5
A
1000-3630(2016)-02-0167-07
10.16300/j.cnki.1000-3630.2016.02.015
2015-03-09;
2015-06-01
自然科学基金(41327004, 41306038, 41376103)、中国高等学校博士点基金(20112304130003)资助项目
魏波(1988-), 男, 黑龙江哈尔滨人, 博士研究生, 研究方向为海底特性声学探测。
李海森,E-mail: hsenli@126.com

