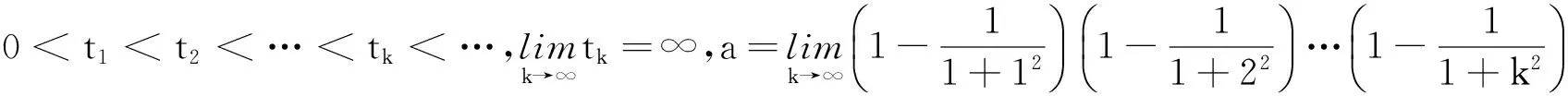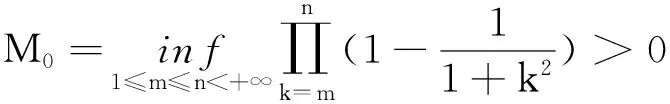一类脉冲时滞模型的一致持久性
蒋 燕,杨喜陶
(湖南科技大学 数学与计算科学学院, 湘潭 411201)
一类脉冲时滞模型的一致持久性
蒋燕,杨喜陶
(湖南科技大学 数学与计算科学学院, 湘潭 411201)
研究了一类非线性脉冲时滞Nicholson飞蝇模型的动力学行为.通过利用比较原理来研究它的一致持久性,得到了该系统一致持久性的充分条件.
Nicholson飞蝇模型;一致持久性;脉冲;时滞
0 引 言
Nicholson飞蝇模型由于其理论和实际意义,已被广泛研究[1].提出了修改后的Nicholson飞蝇模型
N′(t)=-δN(t)+pN(t-τ)e-rN(t-τ),t≥0
(1)
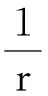
对(1)进行推广,许多学者研究了具有多个时滞的常微分方程
N′(t)=-δ(t)N(t)+
(2)
的动力学性质[2-6].其中文献[2,3]研究了非线性时滞Nicholson模型解的全局吸引性,文献[4-6]对非线性时滞Nicholson模型正周期解的存在性进行了深入的研究,获得了非常多且非常精细的结果.文献[6]研究了模型
的持久性与正周期解的存在性.但是,考虑到生物模型的实际情况,当种群数量经历一个相对较长的光滑变化过程后,由于收获、放养、疾病等其他干扰作用以后,在一定的时刻种群数量会发生突变,由于突变过程同整个发展过程相比非常短暂,对这样的生态系统就需要用具有脉冲作用的微分方程系统,即脉冲微分方程模型来描述和研究.由于脉冲微分方程较之相对无脉冲的微分方程更能准确地描述生态系统中的很多现象.
基于此,我们将研究下面的非线性脉冲时滞微分方程
(3)
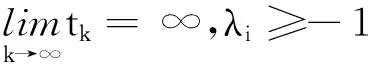
我们首先给出一些记号:对定义在R上的有界连续函数g,g*和g*分别表示:

且记

在本文中,用R+表示非负实数集,C+=C([-r,0],R+)是赋予通常最小上确界范数‖·‖的连续函数空间,记C+=C([-r,0],R+)设t0∈R,σ∈R,如果x(t)是定义在[-r+t0,σ)上的连续函数,定义xt∈C为xt(θ)=x(t+θ),其中θ∈[-r,0].
考虑到模型的生物意义,我们只考虑正解,即考虑初始条件:
xt0=φ,φ∈C+,和φ0>0.
(4)
记x(t;t0,φ)为(3)满足初始条件(4)的解.且令[t0,η(φ))是解x(t;t0,φ)的最大存在区间.
1 一致持久性

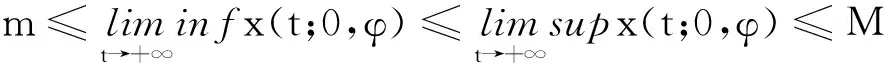
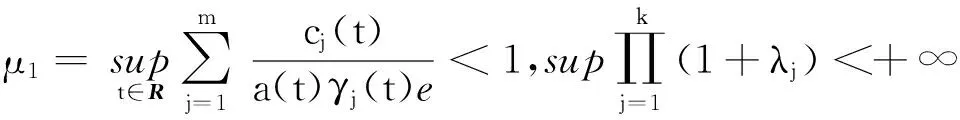
(5)
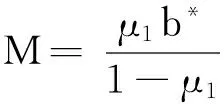
证明记x(t)=x(t;0,φ),
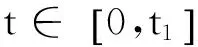
由于x(0)=φ(0)>0,则∀t∈[0,η),x(t)>0.
事实上,若存在θ∈[0,η),使当t∈[0,θ)时,x(t)>0.而x(θ)=0,则当t∈[0,θ)时
从而
令t→θ
矛盾.
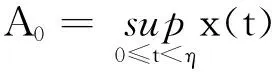
若A0=φ(0),此时η=t1,对t∈[0,t1],(5)成立.
若A0>φ(0),∀η0∈[0,η)满足x′(η0)≥0
由(3)得
从而有
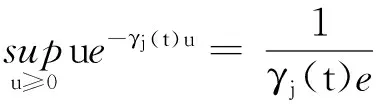
故
从而
故
此时亦有η=t1且当t∈[0,t1]时,(5)成立.设当t∈(tk-1,tk]时(5)成立
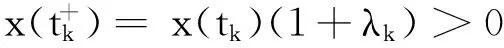
与前面类似可证当t∈(tk,ξ)时,x(t)>0
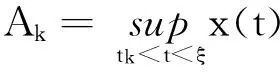
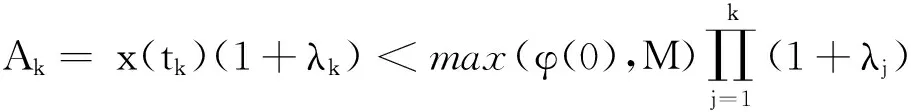
若Ak>x(tk)(1+λk),设ηk∈(tk,ξ)满足x′(ηk)≥0与前面类似可证x(ηk)≤M.
故有ξ=tk+1且∀t∈(tk,tk+1]
x(t) 从而∀t∈(tk-1,tk],(5)成立. 引理2([7])设x(t)在R上有定义,且满足 则 (6) 引理3设x(t)在R上有定义,且满足 则 (7) 证明与引理2类似,从略. 定理1设 β0=min(M0,1)μ0>1 β1=max(M1,1)μ1<1 则系统(3)的解一致持久,其中μ1为引理1所给. 证明:∀φ∈C+,记x(t)=x(t;0,φ) 由引理1知x(t)在[0,+∞)上有定义,且存在常数M(φ)>0,使∀t≥0有 0 x(t) 由(3)知∀t>T时,t≠tj,j=1,2,… 由引理2知当t>T时设tk 则 从而,当t>T时 从而 a≤max(M1,1)(b*+a)μ1=β1(b*+a) 可得 即 tn≥τ 往证当n>N0时 (8) 当n=N0+1时,若存在sn∈(tN0,tN0+1] 使an=x(sn),则 x′(sn)≤0 从而 e-γj(sn)x(sn-τj(sn)) 故 (9) 设sn-τj(sn) 从而有 x(sn)≥(1+λj0)(1+λj0+1)… 从而 故此时(8)成立. 设当n=k>N0时(8)成立 则当n=k+1时,考虑两种情形 情形1若∃sk∈(tk,tk+1]使ak+1=x(sk) 故(8)成立. an≥min((1+λn-1)an-1,m)≥ min((1+λn-1)(1+λn-2)an-2,(1+λn-1)m,m)≥ (1+λn-1)m,m)≥min(M0aN0,M0m,m) 故 则∀ε>0,存在T1>0,当t>T1时 b-ε (10) 由(3)知,当t>0时 由引理3及(7)知,∀t≥T1+τ 从而 (11) 由(9)知,当s≥T1+τ时 (12) 由(11)与(12)知,当t≥T+τ时 从而 由于b≠0,从而 注:当λi≡0(i≥1)时,定理1的条件与文献[6]的定理1的条件一样,但是文献[6]只证明了系统(3)的解是持久的,未说明一致持久性.因此,在无脉冲情形下也推广了文献[6]定理1的结果. 在这一部分,将通过一个例子来说明之前的结论. 例对于如下脉冲时滞Nicholson飞蝇模型: N(t-e4π+sint)e-e4π+|sint|N(t-e4π+sint) N(t-e4π+cost)e-e4π+|cost|N(t-e4π+cost). (13) 则:方程(13)具有一致持久性 证明:由(13)可得 γ1(t)=e4π+|sint|γ2(t)=e4π+|cost| τ1(t)=e4π+sintτ2(t)=e4π+cost 根据定理1,有 β0=min(M0,1)μ0>1 β1=max(M1,1)μ1<1 满足定理1的条件,从而方程(13)是一致持久的. [1]GurneyWSC,BlyteSP,NisbetRM.Nicholson’sBlowfliesRevisited[J].Nature,1980,287:17-21. [2]NicholsonAJ.AnOutlineoftheDynamicsofAnimalPopulations[J].Zool,1954(2):9-65. [3]CookK,DriesscheVP,ZouX.InteractionofMaturationDelayandNonlinearBirthinPopulationandEpidemicModels[J].Math.Biol,1999,39:332-352. [4]ChenY.PeriodicSolutionsofDelayedPeriodicNicholson’sBlowfliesModels[J].CanApplMath.Q,2003(11):23-28. [5]LiJ,DuC.ExistenceofPositivePeriodicSolutionsforaGeneralizedNicholson’sBlowfliesModel[J].ComputApplMath,2008,221:226-233. [6]HouX,DuanL,HuangZ.PermanenceandPeriodicSolutionforaClassofDelayNicholson’sBlowfliesModels[J].ApplMath.Model,2013(37):1537-1544. [7]宋新宇,郭红建,师向云.脉冲微分方程理论及其应用[M].北京:科学出版社,2011. TheUniformPersistenceofaKindofImpulsiveDelayModel JIANGYan,YANGXi-tao (Schoolofmathematics,HunanUniversityofScienceandTechnology,Xiangtan411201,China) Inthispaper,westudythedynamicbehaviorsforaclassofnonlinearimpulsivedelayNicholson’sblowfliesmodels.Byusingthecomparisonprinciple,somesufficientconditionsthatguaranteetheuniformpersistenceofthemodelareobainted. Nicholson’sblowfliesmodel;uniformpersistence;impulsive;delay 2015-06-18 湖南省自然科学基金资助项目(2015JJ2063). 蒋燕(1992-),女,硕士研究生,研究方向:常微分方程. 0175.1 A 1671-119X(2016)01-0049-05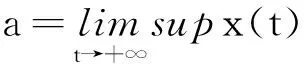
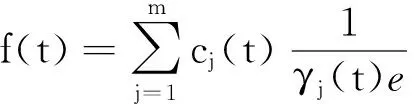
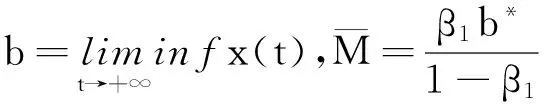
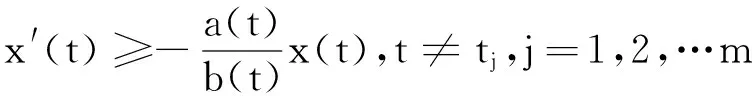
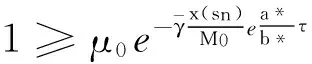
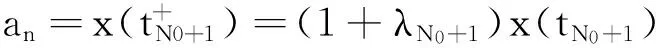
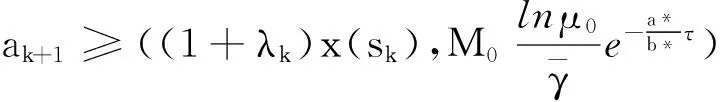
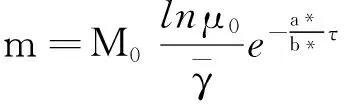
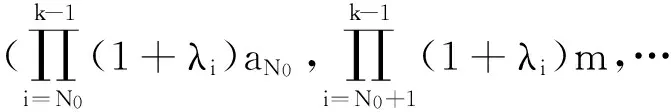
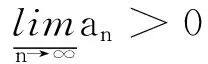
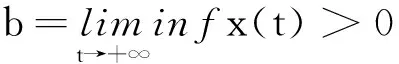
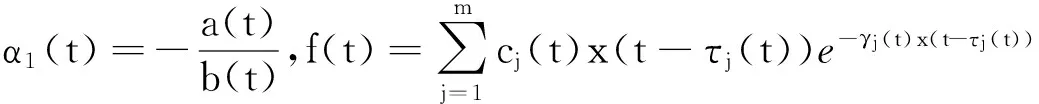
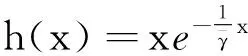
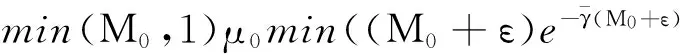
2 应用