某平面相控阵雷达总体结构模态分析*
汪文强,王进军,王德宇,龙文武,2,陈 浩
(1. 武汉滨湖电子有限责任公司技术中心, 湖北 武汉 430077;2. 空军驻华中地区军代表室, 湖北 武汉 430077)
某平面相控阵雷达总体结构模态分析*
汪文强1,王进军1,王德宇1,龙文武1,2,陈 浩1
(1. 武汉滨湖电子有限责任公司技术中心, 湖北 武汉 430077;2. 空军驻华中地区军代表室, 湖北 武汉 430077)
为探究某平面相控阵雷达总体结构的动态特性,采用分步离散再合并的方式建立有限元模型,并运用Lanczoc法获取其模态参数。结果表明:总体结构固有频率规避了自身回转激励频率,满载30 r/min条件下发生共振现象的可能性较小;天线舱体质心相对回转中心存在偏离是导致总体结构1阶频率偏低的重要原因;总体结构前6阶模态参数反映出车载平台、举升结构刚度良好;最大偏离位移出现在天线骨架横纵梁连接处,采用三角肋板优化处理后,偏离位移有效减小。
动态特性;Lanczoc法;模态参数;固有频率
引 言
平面相控阵雷达实现了天线快速扫描的能力,有效地克服了传统机械扫描天线波束指向转换所带来的惯性效应,从而实现对多批、高速、高机动目标的识别与追踪功能。雷达的指示与追踪精度严重依赖于反射面的精度[1],这一现实要求取决于雷达总体结构在不同工况条件下的刚度与稳定性。
近年来,国际信息化军备竞争对雷达总体结构性能指标不断提出新的要求,军用雷达实际的服役环境条件愈为恶劣。雷达总体结构在突防运输、极端脉动风载荷、附加周期性偏载等条件下形成的随机振动效应,极易引起雷达结构及舱内仪表和电子设备的振动响应,甚至引发灾难性工程事故[2]。理论上,雷达结构系统的稳定性由自身固有的模态参数,如频率、阻尼、振型等表征。往往低阶弹性模态反映结构的整体刚度性能,且是控制其振动效应的关键指标,用以评估各部件与系统的动态干扰。
因此,研究如何合理避开工作环境中各种激励频率对雷达总体结构优化设计具有现实的指导意义。
国内外相关领域研究人员在对雷达结构动态特性的研究过程中,往往集中于对天线骨架[3-4]、回转平台
及车架[5]等子系统进行研究,或者是将各子结构系统进行拆解分析,然后再耦联成整体进行分析。显然,由于各子系统无论是在频域还是时域上均有其自身动力特性,连成体系后无法真实反映结构总体的固有属性,其原因主要有:1)子系统振型在连成体系后发生了变化;2)子系统在连接时存在偏差,雷达结构总体的自由度不再是简单的叠加;3)耦联时,子系统各自残余不平衡量的相位差不一致[6]。
雷达结构总体刚度和阻尼决定了自身的稳定性,并在一定程度上影响雷达的电讯性能。鉴此,本文针对雷达总体的振动模态及刚度、结构参数对自身结构的动力学特性的影响进行分析,以期为提高平面相控阵雷达系统的稳定性和安全性提供理论依据。
1 动力学方程求解
研究雷达总体结构动态特性的实质是求解系统在无外力作用下的模态参数,其动力学响应即为自由振动,亦即是在系统内力的驱动下进行的,因此同样遵循牛顿第二定律:
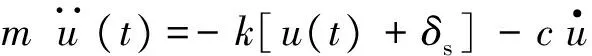
(1)
根据静力平衡有:
mg=kδs
(2)
则:
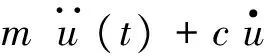
(3)
式中:m为质量;u为位移;k为系统刚度;c为阻尼;f为外力,自由状态下,f为0;δs为伸长量。
多自由度的离散化结构在任意外界激励f(t)的作用下,其振动方程为
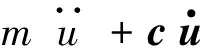
(4)
对式(4)进行拉氏变换:
(s2m+sc+k)u(s)=f(s)
(5)
式中,u(s)及f(s)分别为位移响应及外界激励的拉氏变换,令s=jω,则上式为
(k+jωc-ωm)u(ω)=f(ω)
(6)
引入模态坐标进行解耦,令:
u=pq
(7)
式中:p为振型矩阵;q为模态坐标。则上式可变换为
(k-ωm+jωc)pq=f
(8)
由于振型矩阵相对质量和刚度矩阵的正交关系,将质量矩阵、刚度矩阵、阻尼矩阵分别进行对角化处理,有:
(9)
对式(8)进行求解,分别前乘pT,有:
(ki+jωci-ωmi)q=pTf
(10)
对于相互耦合的n个自由度的系统方程,解耦后的第i个方程为
(11)
则在任意坐标系下,系统的响应可表示为
(12)
而频率ω为
(13)
采用模态归一化振型P,将质量归一化:
PTmP=I
(14)
PmPT=ω2
(15)
则式(6)为
(16)
雷达结构总体在空间上具有多个物理自由度,通过对式(1)~式(16)的推导,不难发现系统多自由度振动的响应,可通过将n个模态坐标下单自由度振动的响应叠加后进行表征。因此,要识别系统在空间上的振动特性,必须求解出系统n阶模态的频率、阻尼及振型。有必要指出,系统的动力响应特征主要由结构的低阶模态决定,且是总体结构设计的重点关注对象[7]。
2 模型建立
本文采用ABAQUS/Standard有限元分析模块对雷达总体结构进行求解。总体结构如图1所示,其中包括天线、回转台、举升装置、车载平台、防风腿等部件。在处理系统振动问题时,数值仿真的本质是将系统结构离散成多个质量与弹簧单元,通过求解矩阵方程求解各阶振型和频率参数,且网格的质量决定离散的合理性和求解的精度。鉴于本文研究的雷达系统结构形式复杂,采取分步离散再合并连接的方式建模[8]:采用三维软件建立整体模型,离散时对各子结构进行独立切分,在关键连接处设置弹簧单元将各子系统连接成整体,且对曲率过小的过渡尺寸进行处理,消除奇异矩阵从而改善运算速度。最终,总体结构被离散成106 116个单元,包含205 175个节点。需要指出的是,在处理结构的动力响应问题时,Lanczoc法表现出更高的精度和效率[9],因此本文采用Lanczoc法进行求解。此外,由于天线舱体主要由高频柜和电子柜组成,质量分布不均,因此在建模时预先提取其空间质心,然后进行等效处理;约束条件设定4条防风腿为固定约束。材料弹性模量E为2.06 × 1011Pa,泊松比ν取0.27,密度为7.85 ×103kg/m3。
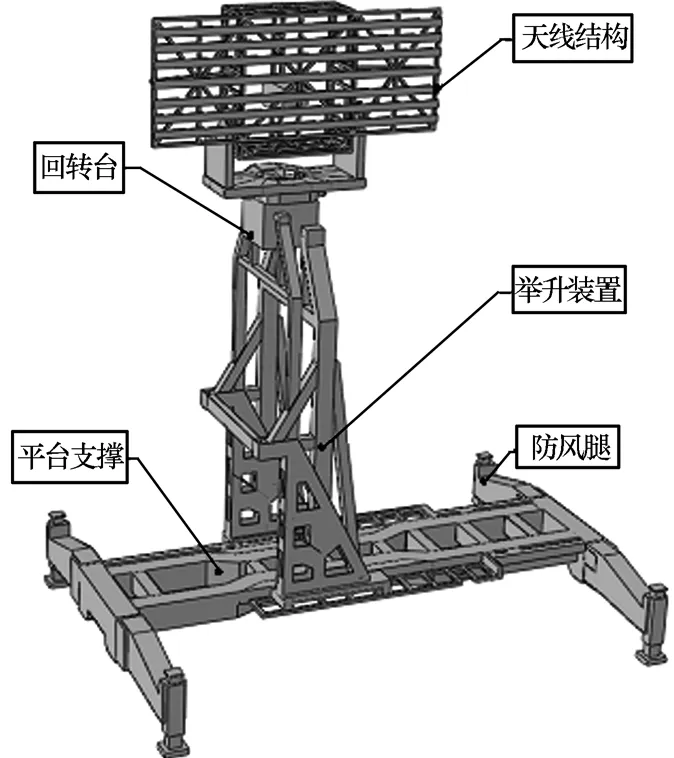
图1 雷达系统总体结构
3 结果分析
为满足战术指标要求,本文所研究的雷达天线要求在工作状态中实现30 r/min的转速且保证平稳工作,其激励频率为0.5 Hz。为避免共振耦合现象,雷达总体结构1阶模态频率至少要高于这一值。
图2给出了雷达总体结构的6阶振型云图。为了更直观地对结果进行分析,后处理过程中将变形缩放系数设定为100倍。
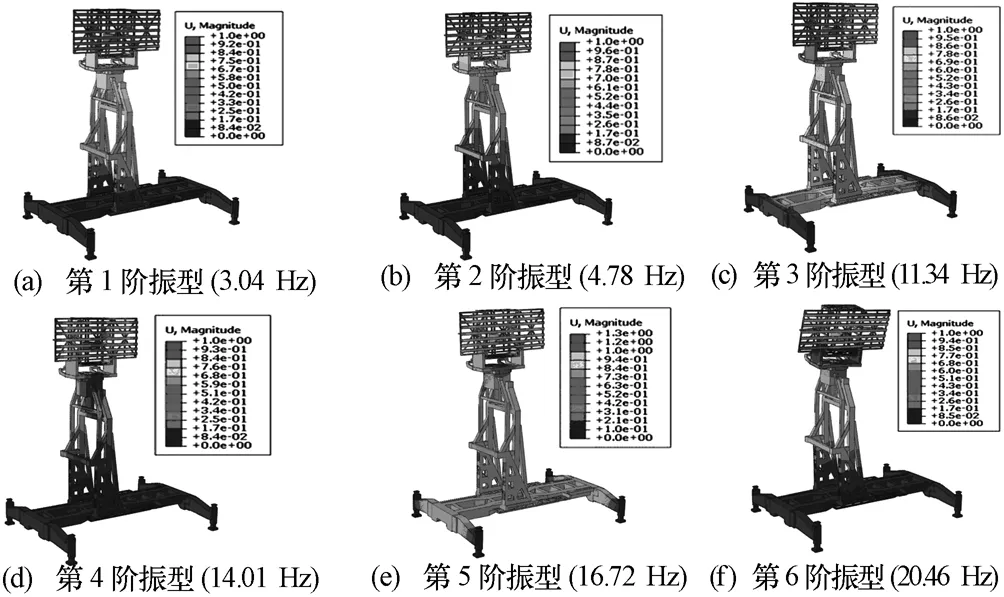
图2 雷达总体结构1~6阶振型云图
图2(a)为总体结构1阶振型。由图可见,车架部位未发生响应,说明车载平台刚度良好;天线骨架相对其他部位出现明显的横向偏转现象。究其内因,主要由以下几点构成:1)从总体结构几何空间质量分布角度分析,天线结构为梁的自由端(相对地面8.05 m),处于无约束状态,容易形成悬臂梁式振动效应;2)相对举升结构,天线结构质量较大;3)天线骨架与回转平台通过支轴连接,横向刚度不足。鉴此,为提高天线骨架的横向扭转刚度,应合理减轻骨架消极质量,且提高天线与回转平台之间的连接刚度。此外,图2(a)~(f)振型结果中显示天线骨架左上侧横梁与纵梁连接处位移出现最大值,说明其连接刚度较差,有必要提高这一位置的抗弯刚度,如增加三角肋板进行加固。图3为横纵梁经加固处理后节点前20阶对应的位移。不难发现,加固后位移量相对天线阵面尺寸较小,并不影响整体刚度。
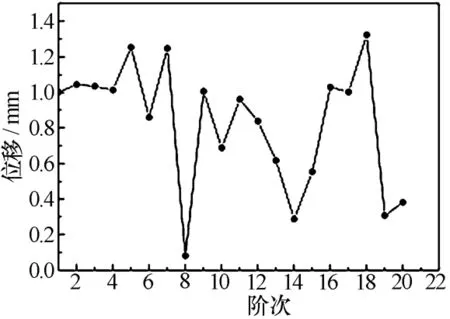
图3 天线横纵梁连接加固后节点位移图
图2(b)~(e)为天线与举升结构的耦合扭转振型。由图可见,天线结构相对举升结构发生明显的横向偏转,这一结果直观地反映出天线骨架相对回转平台中心轴线质量分配不均引起横向刚度不足,这可能导致整个天线结构在回转速度较高时出现偏转现象,甚至在极端风振策动激励下工况更为恶劣。天线总体结构质量分布不均主要由舱体内部高频柜和电子柜质量偏差及实际安装位置引起。图2(f)显著地反映出这一效应,由于整体质心相对回转中心偏移,导致天线舱体整体纵向摆动幅值明显。显然,要有效改善整体扭转刚度,需深入研究天线舱体内电子设备的合理布局,使整体质心向回转中心靠近。值得指出的是,图2(a)~(f)中不难观察到举升结构总体变形量较小,这是由于举升结构整体采用三角结构进行约束,有效地提高了整体抗扭刚度。
4 结束语
本文针对某平面相控阵雷达动态特性进行了研究,得出以下结论:
1)总体结构的固有频率规避了自身回转激励频率,在满载30 r/min条件下发生共振的可能性较小。
2)总体结构1阶频率偏低,主要由于天线舱体质心相对回转中心存在偏离现象,要提高整体刚度需有效减轻天线舱体消极质量及合理控制质心位置。
3)总体结构前6阶模态参数反映出车载平台、举升结构刚度良好;最大偏离位移出现在天线骨架横纵梁连接处,采用三角肋板优化处理后,偏离位移有效减小。
[1] 赵宏伟. 某雷达天线座俯仰组合轴刚度特性分析[J]. 电子机械工程, 1997(1): 55-59.
[2] 陈云飞, 刘维明. 天线座固有频率的计算分析[J]. 无线电电工, 1997, 27(3): 39-42.
[3] 杨振宙. 机动式空馈相控阵测量雷达结构误差的分析[J]. 电子机械工程, 2007, 23(4): 10-13, 43.
[4] 周雷, 任翠锋. 高机动天线结构设计[J]. 机械与电子, 2011(4): 78-80.
[5] 贺鹏. 雷达平台骨架的计算与试验分析[J]. 电子机械工程, 2009, 25(4): 22-25.
[6] 胡海岩. 机械振动基础[M]. 北京: 北京航天航空大学出版社, 2005.
[7] 张小安, 张艳. 天线座结构的实验模态与理论模态的分析比较[J]. 电子机械工程, 2005, 21(1): 37-40.
[8] 杨瑞峰, 崔志琴. 大功率柴油机组合结构建模技术研究[J]. 内燃机工程, 2003, 24(3): 20-22.
[9] 吴俊清. 某军用发动机振动模态的实验研究与计算[J]. 兵工学报, 2005, 26(4): 492-495.
汪文强(1988-),男,助理工程师,主要从事雷达总体结构设计。
王进军(1978-),男,高级工程师,主要从事雷达总体结构设计。
王德宇(1978-),男,高级工程师,主要从事雷达总体结构设计。
龙文武(1982-),男,工程师,主要从事雷达电子设备设计。
陈 浩(1985-),男,工程师,主要从事雷达传动系统设计。
Modal Analysis of the Holistic Structure of a Planar Phased Array Radar
WANG Wen-qiang1,WANG Jin-jun1,WANG De-yu1,LONG Wen-wu1,2,CHEN Hao1
(1.WuhanBinhuElectronicCo.,Ltd.,Wuhan430077,China;2.AirMilitaryRepresentativeOfficeinCentralChinaRegion,Wuhan430077,China)
In order to research the dynamic characteristics of the holistic structure a planar phased array radar, the method of discrete distribution then merging is applied to establish the finite element model of the structure, and the modal parameters are obtained by the Lanczoc method. The results show that the natural frequency of the structure avoids its own rotating excitation frequency and the possibility of resonance accident under the condition of 30 r/min is small; that the centroid of antenna module has deviation from the rotary center is the important factor that causes the first order frequency low; the modal parameters of first to sixth order reflect that the vehicle platform, lifting devices possess good stiffness; the maximum deviation displacement appears at the horizontal and vertical antenna frame girder joint, and it is decreased effectively after the optimization by triangle floor structure.
dynamic characteristics; Lanczoc method; modal parameters; natural frequency
2016-05-09
TN820.8+8
A
1008-5300(2016)04-0058-04

